一类非线性斯图谟—刘维尔问题正解的存在性
2015-07-02王其申
王其申,陈 健,何 敏
(1.安庆师范学院 物理与电气工程学院,安徽 安庆 246133; 2.安庆师范学院 数学与计算科学学院,安徽 安庆 246133)
一类非线性斯图谟—刘维尔问题正解的存在性
王其申1,陈 健2,何 敏1
(1.安庆师范学院 物理与电气工程学院,安徽 安庆 246133; 2.安庆师范学院 数学与计算科学学院,安徽 安庆 246133)
本文讨论了非线性斯图谟-刘维尔方程[p(x)u′(x)]′+f[u(x)]=0在两端固定边条件下的边值问题,当p(x) 是区间[0,1]上的分段线性函数时,其正解存在。
非线性斯图谟-刘维尔边值问题;分段线性函数;正解;存在性
关于非线性斯图谟-刘维尔方程的边值问题,它的正解的存在性有着重要的理论意义和应用价值。此问题的研究始于L. H.Erbe[1],其后,国内外学者就此课题开展了广泛而深入的研究[2-4],其中,郭大钧[4]深入研究了以下边值问题
(1)
当p(x)∈C1[a,b],p(x)>0时正解或多解的存在性。该论著有力推动了国内这一研究领域的进展[5-7]。已有文献都是在p(x)一阶连续导数存在的前提下讨论的,而对工程实际中出现的非线性斯图谟-刘维尔边值问题,常会遇到p(x)或p′(x)具有某种间断性的情况,因此需要讨论p(x)的一阶导数不存在时方程(1)的非线性边值问题正解的存在性。陈健等人[8]讨论了当p(x)是分段常数情况下非线性斯图谟-刘维尔方程第一边值问题正解的存在性,得出了肯定的结论。本文主要讨论当p(x)是分段线性函数时,下列非线性斯图谟-刘维尔方程边值问题正解的存在性:
(2)
其中f∈C(R+,R+),f(0)=0,
不失一般性,可设常数c满足0
1 预备知识
1.1 边值问题的格林函数
仿照文献[4],采用通解组合法,可以解出边值问题(2)所对应的齐次方程的Green函数是:
当0 (3.1) 而当c≤s<1时, (3.2) 其中, (4) 引理1 设Gij(x,s)(i=1,2;j=1,2,3)为齐次问题(2)的形如式(3.1)和(3.2)的Green函数,则 (i)Gij(x,s)>0,∀(x,s)∈(0,1)×(0,1);(ii)G11(x,x)=G12(x,x),G22(x,x)=G23(x,x); (iv)Gij(x,s)≥μGi(s,s) ,其中,0<ε 证明 因为a1x+p1>0(0≤x≤c),a2x+p2>0(c≤x≤1)和ω<0,性质(i)成立,性质(ii)可直接被检验,因此只要证明(iii)和(iv)。 同理有G2j(x,s)≤G2(s,s) (j=1,2,3),即(iii)成立。 (iv) 当0<ε 同理 因为c+ε≤1-c+ε,当c-ε≤x≤c+ε时性质(iv)亦成立。 1.2 非线性S-L边值问题的积分形式解 考察下列边值问题 (5) 引理2 若u(x)表示为 (6) 则u(x)是边值问题(5)的解,即u(x)满足方程(5)且u(x)∈C2[0,1]。 证明 把(6)式两边对x求一次导,利用引理1的性质(ii)以及Green函数的连续性,得 1.3 范数形式的锥拉伸与锥压缩不动点定理 (H1) ‖Au‖≤‖u‖, ∀x∈P∩∂Ω1; ‖Au‖≥‖u‖, ∀x∈P∩∂Ω2。 (H2)‖Au‖≤‖u‖, ∀x∈P∩∂Ω2; ‖Au‖≥‖u‖, ∀x∈P∩∂Ω1。 那么,A在P∩(Ω2Ω1)中必具有不动点。 在这些条件下,必有正函数u(x)∈C2[0,1]满足边值问题(5)。 证明 引理2表明,边值问题(5)属于C2[0,1]的解和方程 (7) 当Green函数的表达式由(3.1)式和(3.2)式给出时属于C[0,1]的解等价。设P*={u(x)|u(x)∈C[0,1],u(x)≥0},对于0<ε (8) 不难检验P*与Pε*都是空间E=C[0,1]中的锥,同时A:P*→P*全连续。令u(x)∈P*,由引理1的性质(iii) 和引理2可以推出 ∫0cG1(s,s)f[u(s)]ds+∫c1G2(s,s)f[u(s)]ds (9) 再由引理1的性质(iv),有 μ{∫0cG1(s,s)f[u(s)]ds+∫c1G2(s,s)f[u(s)]ds} (10) A(Pε*)⊂Pε*,0<ε (11) 利用f(0)=0以及定理1的条件(ii),可知∃r>0,使得当0 ∀x∈(0,1) 进而就有 ‖Au‖≤‖u‖,∀u(x)∈P*,‖u‖=r (12) 另一方面,定理1的条件(iii)表明,∃η>0 ,使当u≥η时,f(u)≥u/M恒成立。设 Rε=max{2r,η/μ} (13) (14) 因为F′(ε)=μ′(ε)h(ε)+μ(ε)h′(ε),所以当ε→0时F′(ε)>0,而当ε→c时F′(ε)<0。可见,∃ε0∈(0,1),使F′(ε0)=0,从而F(ε)在ε=ε0时达到其最大值。记该最大值为M=F(ε0)。于是在(14)式中,取ε=ε0得 (15) 由Gi(x,s)的性质,显然有u(x)>0,∀x∈(0,1),定理得证。 以上讨论表明,对于非线性S-L方程的第一边值问题,当其系数p(x)为分段线性函数时,其正解是存在的。 [1]L. H.Erbe,H.Wang.On the existence of positive solutions of ordinary differential equations [J].Proc.killer.Math.Soc., 1994, 120(8): 743-748. [2] D. O. Regan.Theory of Singular Boundary Value Problems[M].Minnesota: Scientific World, 1994. [3] 姚庆六. Sturm-Liouville边值问题的正解存在性[J]. 数学物理学报, 2002, A(2): 145-149. [4] 郭大钧, 孙经先, 刘兆理. 非线性常微分方程泛函方法[M].济南: 山东科学技术出版社, 2005. [5] 李高尚, 刘锡平, 贾梅, 等. 一类微分方程组的非齐次Sturm-Liouville边值问题解的存在性[J]. 应用泛函分析学报, 2009, 11(1): 79-85. [6] 孙经先, 张国伟. 奇异非线性Sturm-Liouville问题的正解[J]. 数学学报, 2005, 48(6): 1095-1104. [7] 侯丽芳, 李宇华. 二阶Sturm-Liouville边值问题解的存在性[J]. 山西大学学报(自然科学版), 2009, 32(2): 168-171. [8] 陈健, 沈娟, 王其申. 一类非线性斯图谟-刘维尔方程两点边值问题解的存在性[J]. 应用数学学报, 2013, 36(2): 298-305. Existence of Positive Solutions for a Class of Nonlinear Sturm-Liouville Boundary Value Problems WANG Qi-shen, CHEN Jian, HE Min (1.School of Physical and Electrical Engineering, Anqing Teachers College, Anqing 246133, China; 2.School of Mathematics and Computation Science,Anqing Teachers College,Anqing 246133,China) In this paper,the existence of positive solutions for the first boundary value problems of the nonlinear Sturm-Liouville equation [p(x)u′(x)]′+f[u(x)]=0 is discussed, wherep(x) is a segmentation linear function in interval [0, 1]. nonlinear Sturm-Liouville boundary value problems, segmentation linear functions, positive solutions, existence 2015-04-14 王其申,男,安徽桐城人,安庆师范学院物理与电气工程学院教授,主要从事结构动力学和应用数学领域的研究。 时间:2016-1-5 13:01 网络出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.001.html O32 A 1007-4260(2015)04-0001-06 10.13757/j.cnki.cn34-1150/n.2015.04.001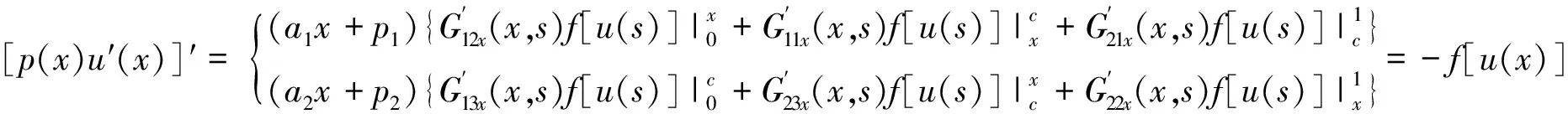
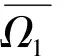
2 主要结果
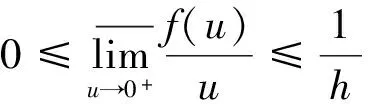

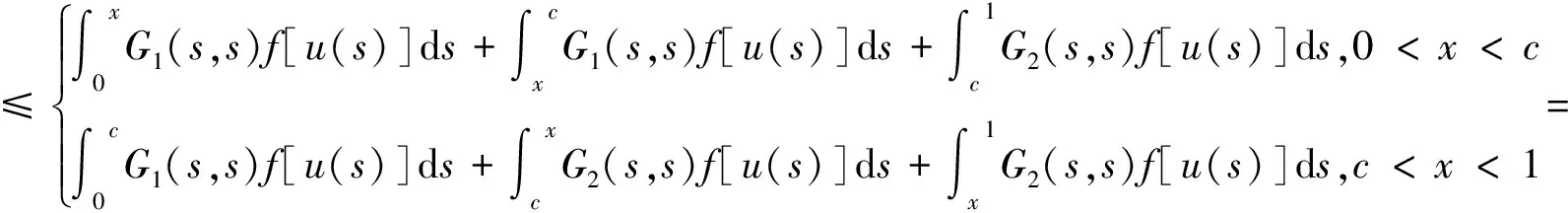
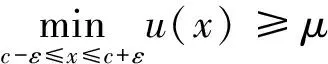

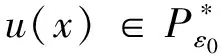

3 小结
