周 娟，李 超

（湖北民族学院科技学院，湖北 恩施 445000）

基于卢卡西维茨多值演算的模态逻辑推理机

周 娟，李 超

（湖北民族学院科技学院，湖北 恩施 445000）

模态逻辑广泛应用于人工智能领域，但没有实际有效的推理机.针对上述问题，研究了模态逻辑中演绎推理的方法，该方法用必要的形式化方法将模态逻辑转换为卢卡西维茨多值逻辑，再将卢卡西维茨多值逻辑转换为布尔逻辑.结果表明和其他方法相比，该推理机在模态逻辑中具有普适性、计算简单性、推理规则应用的非限制性.

卢卡西维茨多值演算；模态逻辑；推理机

模态逻辑究必然、可能及其相关概念的逻辑性质.在模态家族中最熟悉的逻辑是从一个被称为K（Saul Kripke）的弱逻辑建立的.K是古典命题演算增加以下初始规则和公理的直接扩张．

初始规则（也称必然化规则）：如果A是K的定理，则□A是定理．

公理 □（A→B）→（□A→□B）．

（这里使用“A”和“B”表示系统中任何为真的公式．）根据必然化规则，逻辑中的任何定理必然为真．

可能性算子◇通过必然性算子□定义为◇A＝┐□┐A．在系统K中，算子◇和□的特性非常类似于一阶逻辑中的量词∀（所有）和∃（一些）．例如，通过□定义◇反映了∀xA与┐∃x┐A的等价性．□和◇之间的这种类比可以在文献［1－2］中找到．

模糊模态逻辑是通过指定模糊测度从模态逻辑公式推导而来的．例如，□xy［μ≥0．6］表示公式□xy为真的可能性为0．6．在模糊模态系统中没有一个唯一的方法来构建模态系统的推理机制，比如：公理化方法［3］，归结原理［4］，根岑（Gentzen）系统的自然演绎方法［5］，表列方法［6］，其他方法［7］等，以上方法具有非普适性（相对于非经典逻辑），计算复杂性，以及应用推理规则的限制性.

在A.Mironov［8］中模糊克里普克模型被视为基于其在系统K中严格推论的推理规则，比如：□α（A→B）→（□αA→□αB），其中α是相应公式的模糊测度．因为不同的公式有不同的模糊真值αi，所以考虑具有多层次β1，β2，…，βq的原公式集的模糊子集S（β1），S（β2），…，S（βq），其中包括模糊真值α≥βi的所有的公式的子集S（βi），是合理的．模糊模态公式φα的一般推断应该在每个βi≤α的子集S（βi）中都成立．

在Z.Zhang等［9］中使用了不同的方法，主要思想是对给定的模糊模态系统用标准的一阶逻辑推理代替模糊推理.在Z.Zhang等［9］中使用的模糊推断定义实际上类似于在本文中使用的定义.

在本文中，提出一个新颖的方法实现推理机［10］，该方法采用卢卡西维奇多值逻辑为理论背景和实践基础．它保证了推理过程的普适性．

1 卢卡西维茨的多值逻辑

使用模态逻辑和相应的卢卡西维茨多值逻辑之间的关系，将给定的模态逻辑转换为卢卡西维茨逻辑，在R·Sushko的研究基础上［11］，再用相应的推理方法转换为布尔逻辑.根据文献［10］本文有所缩写.

1.1 模态逻辑和卢卡西维茨三值逻辑之间的联系

为了构建模态和模糊模态逻辑推理，先定义在模态逻辑系统中什么是真（假）公式．考虑这样一个建模方法，这个方法研究模型M的解释集合IM＝（I1，I2，…，Iz），解释包含了所有可能模型变量值的组合，使得对于每一个Iα、Iβ至少有一个变量在Iα和Iβ中有不同的真假值．最简单的情况是将IM划分为两个子集I1和I0，使IM＝I1∪I0，I1∩I0＝∅．每一个子集定义了基本的逻辑演算公式，并且对于任意一个基本公式φ断言，φ在I1中为真，在I0为假．在这种情况下，公式φ允许任意一个来自I1的解释．假设φ和ε是两个公式，分别对应解释Iφ和Iε．那么以下内容是合理的：

定义1 公式在模型M中是真的，只要其允许所有可能的解释IM．

用卢卡西维茨三值逻辑公式代替模态公式，即，卢卡西维茨三值逻辑可被视为模态逻辑一种模型．在卢卡西维茨三值逻辑中公式x有三个值：val（x）＝｛0，1／2，1｝，其中0代表不可能的，1／2－偶然的，1－必然的（或者也可以换种表达方式：val（z）＝｛0，1，2｝，其中val（z）＝（n－1）·val（x））［12－13］．

在后续的内容中采用：

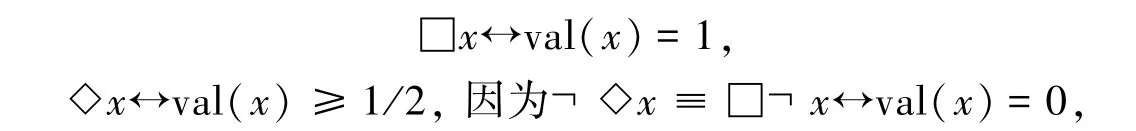
上面给出的在□x，◇x和卢卡西维茨三值逻辑之间的关系已经被A.Tarski证明了［14］，但由于方法的特殊性，本文将给出直接演算证明．

借助于从模态公式到等价卢卡西维茨公式的转换来执行计算．假设给定以下公式：

令α［μ（α）］表示一个只允许val（α）≥μα解释的公式．μα可以被视为公式α的不确定性的值．得到以下结果：

式（1）和（2）可改写如下：

像文献［10］中提到的方法，用二元矢量公式（x1，x2），（┐x2，┐ x1），（y1，y2），（┐ y2，┐ y1）对应地替换三值公式x，┐ x，y，┐ y，即：

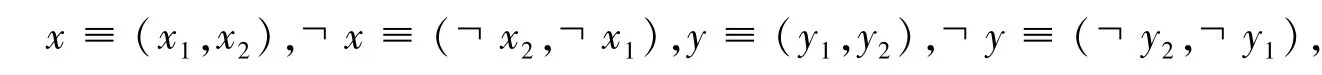
并使用以下三值公式和矢量公式之间的对应关系：

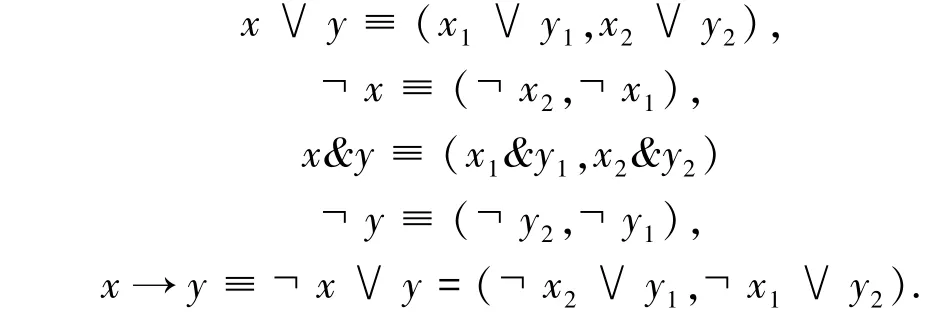
用卢卡西维茨三值逻辑运算的真值表论证这些替换．式（3）和（4）可改写如下：

即获得了等价的布尔系统.因此，通过使用卢卡西维茨的三值逻辑，模态系统可以被置换为等效的布尔系统．本次置换的合理性在另文中论证．

注意：对于任意一个公式α，卢卡西维茨的三值逻辑不允许解释α＝（α1，α2）＝（0，1）．因此，在上述系统还需要添加以下公式：

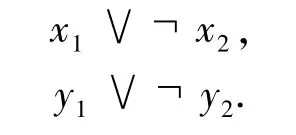
需要注意的是，例如，

1）当x1＝1，x2＝0（val（x）＝0．5）时，公式□（x∨┐ x）＝□（x1∨┐ x2，x2∨┐x1）为假．因此，□（x∨┐x）不是真的模态公式．

2）□x∨┐□x为真，因为□x允许（1，1），并且┐□x允许（0，0）和

（1，0）．从观察同样可以得出 （1，1）∨◇┐ x＝（1，1）∨◇┐ （x2，x1）＝（1，1）∨（0，0）∨（1，0）．

3）◇（x∨┐ x）＝◇（x1∨┐ x2，┐ x1∨x2）＝（1，1）∨（1，0）＝x1∨┐ x2．对于三值逻辑中的x，这个公式允许所有可能的解释（0，0），（1，0），（1，1），因此，◇（x∨┐ x）为真．

4）公式□（◇x∨┐ x）＝□（（（1，1）∨（1，0））∨（┐ x2，┐ x1））＝□（x1∨┐x2，∗）＝x1∨┐x2允许每个可能的值，即，□（◇x∨┐x）为真．为了达到系统化的目的，用类似的公式，比如▽（▽z∨α），▽（▽z∧α），其中▽表示或者◇或者□，z表示三值公式，α表示有两个可能的值0和1的严格的布尔变量，表示下面的关系：

因此，□（◇x∨┐ x2∧┐ x1）＝□（◇x）∨┐ x2∧┐ x1＝□x1∨┐ x2∧┐ x1＝x1∨┐ x2∧┐ x1＝x1∨┐ x2．同一类型的另一个例子：

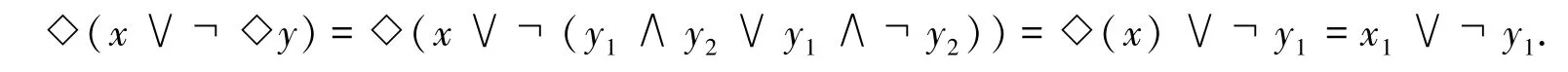
使用α作为一个严格的布尔变量，这些推理的合理性是基于Shannon的公式［15］：

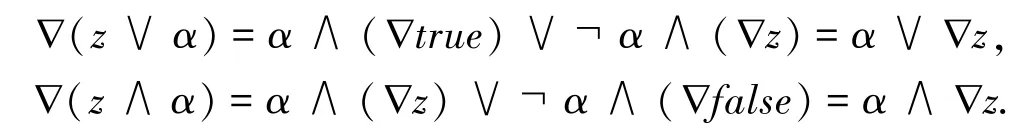
1.2 方法的推广

为了在模糊模态逻辑中应用上述方法，将其推广到k（k＞3）值逻辑中．先考虑当k＝4，k＝5时公式的表示方法．

在k＝4的情况下使用向量：

其否定形式：

和真值：

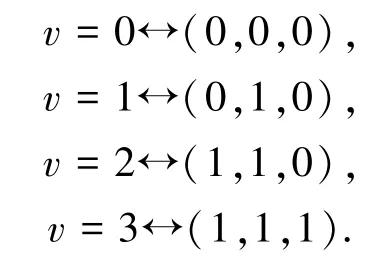
来表示．

在k＝5的情况下的向量表示如下：

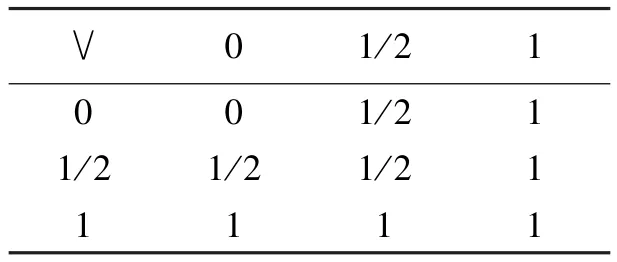
表1 析取真值表Tab.1 The truth table of disjunction

表2 合取真值表Tab.2 The truth table of conjunction

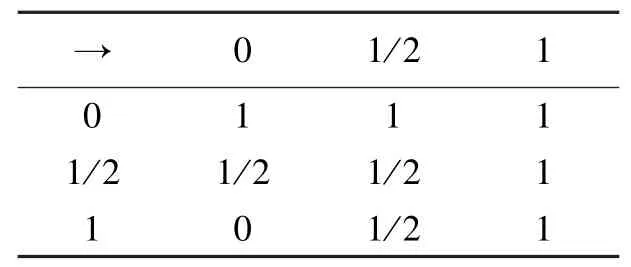
表3 蕴含真值表Tab.3 The truth table of implication

表4 否定真值表Tab.4 The truth table of negation

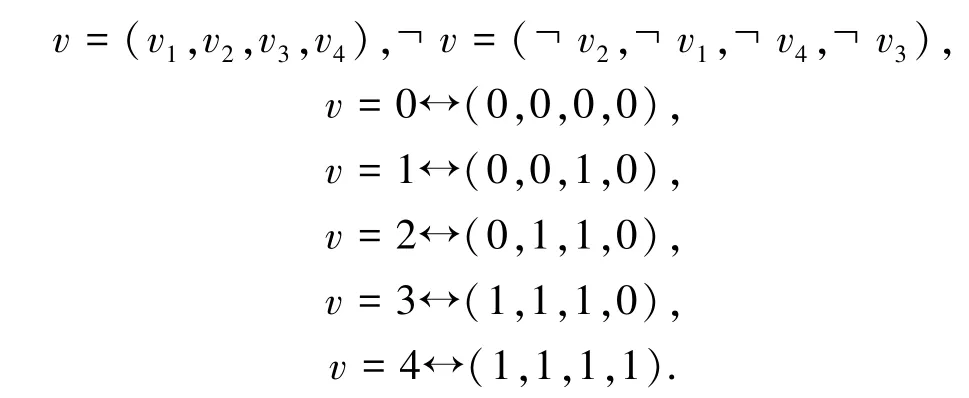
一般情况下，向量可以表示为如下：

满足val（┐v）＝n－val（v）＋1的否定形式┐v．

通过用满足实际应用的多值逻辑值近似模糊值的方法，本文研究方法的关键是在模态逻辑中建立推理机．应当指出的是，直到现在在模糊逻辑中建立推理机的问题还是没有得到圆满解决．Mamdani［16］和类似方法考虑的逻辑规则形式如下：R：如果X＜i＞那么Y（μY）

同时考虑到规则的确定性测度μY．为了应用规则需要定义类似的测度μX，该测度来自于规则R且在输入向量Xt和X＜i＞之间．在一般情况下，μX没有被提前定义且超出逻辑演算的范围．

本文提出的推理机简化了计算复杂性，以不确定测度μα≥2的5－值逻辑公式α＝（α1α2α3α4）为例说明．很容易记录所有的解释，这些解释以惟一项α2的形式被α允许，因为在＜0110＞，＜1110＞和＜1111＞中α2＝1；当α2＝0时在＜0000＞，＜0010＞中不被μα≥2允许，即α＝（α1α2α3α4）［μα≥2］→α2．再看一个例子，如果α＝（α1α2α3α4）［μ≥1］，那么被α允许的解释表示为项α1＝1等．这一观察结果表明，多维公式不确定性测度的使用不会导致增加公式表示的复杂性，把该结果用REF∗表示［17］．

1.3 推理机的应用

举例说明推理机的应用．证明或反驳命题，可以从公式α∨β［μ＝1］，┐α∨β［μ≥0．5］推出公式β［μ≥0.5］．

用向量的形式改写α∨β，如下所示：

由于公式的测度μ等于1，则式（6）等价于：

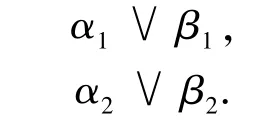
第二个公式用向量表示如下：

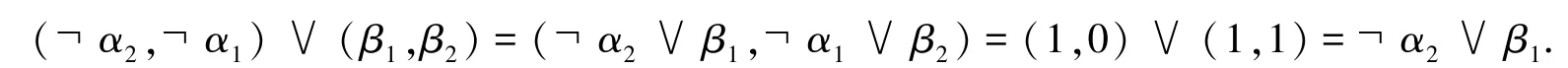
本例中的前提用析取的形式表示如下：

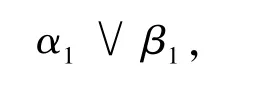
证明由式（7）推出β＝（β1，β2）［μ≥0．5］（即（1，0）∨（1，1）或仅仅β1）．可以容易地用归结原理完成，β1的确可由式（7）推出．

2 结论

本文只提供了一个近似的推理方法，因为它使用固定的逻辑值，而不是模糊逻辑中的连续值．这种方法证明了当n→∞时n值卢卡西维茨逻辑和模糊逻辑之间是有关联的．本文是阶段性的研究成果，模态逻辑和卢卡西维茨的三值逻辑的相符性将在另文中详细讨论．另外，关于该方法在模糊模态逻辑中的进一步应用，也将展开更深入的讨论．

［1］Blackburn P，Johan F.A.K，an B，et al.Handbook of modal logic，volume3（Studies in Logic and practical Reasoning）［M］.Netherlands：Elsevier，2007：3－12.

［2］Eric Pacuit.Notes in Modal Logic［EB／OL］.（2009－1－28）［2015－6－18］.http：／／www.docin.com／p－759520501.html.

［3］李骏，王国俊.基于支持度理论的广义Modus Ponens问题的最优解［J］.软件学报，2007，18（11）：2712－2714.

［4］NivelleD H，Schmidt R A，Hustadt U.Resolution－based methods for modal logics［J］.Logic Journal of the IGPL，2002，10（1）：265－292.

［5］陈晓平.自然演绎逻辑导论［M］.广州：中山大学出版社，2006：102－103.

［6］Jarmuz·ek T.Tableau Metatheorem for Modal Logics［M］.Germany：Springer International Publishing，2014：103－126.

［7］何映思.模糊推理方法及模糊逻辑形式系统研究［D］.重庆：西南大学，2011.

［8］Mironov A M.Fuzzy modal logics［J］.Fundamental and Applied Mathematics，2003，9（1）：201－230（In Russian）.An English Translation：Journal of Mathematical Sciences，2005，128（6）：3461－3483.

［9］Zhang Z，Sui Y，Cao C.Description of Fuzzy First－Order Modal Logic based on Constant Domain Semantics［C］／／Proc of RSFDGrC（Rough Sets，Fuzzy Sets，Data Mining and Granular Computations，Regina），Canada，2005.

［10］German O V，Samko R A，German Yu O.An inference system for a fuzzy logic on the basis of multi－valued Lukasiewicz calculi［J］.Works of the Belarusian University of Technology（Minsk，Belarus），Natural Sciences and Informatics，VI，2010，18：190－193（in Russian）.

［11］Karpenko A S.Lukasiewicz Logics and prime numbers［M］.Moscow：Science，2000：46－98（in Russian）.

［12］吴洪博.Lukasiewicz命题逻辑中公式的Γ－真皮理论和极限定理［J］.中国科学：信息科学，2014，44（12）：1542－1559.

［13］周建仁.Lukasiewicz命题逻辑系统中真度的等价定义及相关性质［J］.工程数学学报，2013，30（4）：580－590.

［14］Ivin A A.Modal Theories of Jan Lukasiewicz［M］.Moscow：Russian Academy of Sciences，Philosophy Institute，2001：8－31（In Russian）.

［15］王庆平，王国俊.多值Lukasiewicz逻辑公式的范式表示和计数问题［J］.软件学报，2013，24（3）：433－453.

［16］Babuska R.Fuzzy and neural control disc course lecture notes［M］.Netherlands：Delft University of Technology，2009：165－187.

［17］German O V.Non－classical logical calculi［M］.The Republic of Belarus：BSUIR，2012：21－25（in Russian）.

责任编辑：时 凌

Inference Machine for Modal Logics Based on Lukasiewicz Multivalued Calculi

ZHOU Juan，LI Chao
（College of Science and Technology，Hubei University for Nationalities，Enshi 445000，China）

Modal logic is widely used in artificial intelligence，but there is not a practically efficient infer⁃ence machine in the modal logic.In this paper an inference approach to making inferences in modal sys⁃tems is studied.The approach is to convert modal logic into Lukasiewicz multi－valued logic，then into Boolean logic with a necessary formalization technique.The main advantages of the approach are univer⁃sality，computational simplicity and non－restrictions on application of the inference rules.

multi－valued Lukasiewicz calculus；modal logic；inference machine

TP18

A

1008－8423（2015）03－0285－04

10.13501／j.cnki.42－1569／n.2015.09.015

2015－08－31.

周娟（1986－），女，硕士，主要从事模态逻辑研究.