基于bius变换的五次有理PH曲线C2 Hermite插值
2015-06-19李少华白瑞峰
丁 晨, 唐 烁, 李少华, 白瑞峰
(合肥工业大学 数学学院,安徽 合肥 230009)
丁 晨, 唐 烁, 李少华, 白瑞峰
(合肥工业大学 数学学院,安徽 合肥 230009)


Pythagorean-hodograph(PH)曲线是一类特殊的多项式曲线,由文献[1]在研究等距曲线过程中提出。PH曲线不但保持了与标准B样条表示和Bézier表示的完全一致性,而且具有多项式曲线无法拥有的优点,如PH曲线的弧长能表示成参数多项式函数,PH曲线的等距线能表示成有理形式。这些性质使得PH曲线在CAD/CAM、CAGD、CNC中有着广泛的应用,如机器人路径的设计、公路铁路的设计、曲面的裁剪等[2-4]。
1 预备知识
其中,a、b、c、d为复数,且ad-bc≠0。其逆变换与一阶导数分别为:
定义1 给定平面参数多项式曲线p(t)=(x(t),y(t)),如果存在多项式σ(t),使得(x′(t))2+(y′(t))2=σ2(t),即(x′(t),y′(t),σ(t))构成勾股数,将平面参数多项式p(t)称为平面Pythagrean-hodograph曲线,简称PH曲线[1]。
引理1a(t)、b(t)、c(t)为多项式,且max[dega(t),degb(t)]=degc(t)>0,满足PH条件a2(t)+b2(t)=c2(t),当且仅当a(t)、b(t)、c(t)能用实多项式u(t)、v(t)、w(t)表示为[1]:
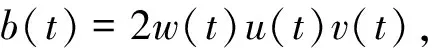
其中,u(t)、v(t)互素,即(u(t),v(t))=1;w(t)是首一多项式。
引理2 PH曲线可以表示为[1]:
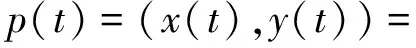
引理3 如果多项式曲线r(t)是PH曲线,当且仅当存在实多项式h(t)和复多项式w(t),使得[10]:
2 插值问题的描述
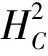
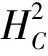
(1)
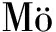
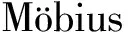
(2)
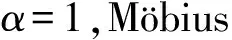
3 五次有理PH曲线C2Hermite插值的构造

其在复平面上对应地可表示为:
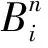
(3)
其中,w(t)、G(t)分别为实、复系数多项式。
为了得到次数最低且可处理拐点的PH曲线,取
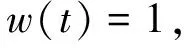
其中,a、b、c为复常数。则
(4)
将(4)式展开,并利用如下积分关系式:
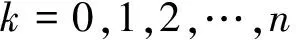
(5)
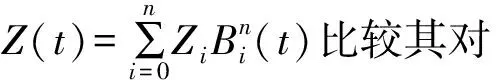
Z4=Z3+bc/10,Z5=Z4+c2/5
(6)
对(4)式求导可得:
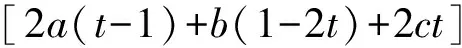
(7)
由(2)式、(7)式得:
(8)
方程组(8)式化简为:
(9)
利用数学工具Matlab中的Slove可以求出方程组(9)式中相应的a、b、c。
由此得到五次多项式PH曲线,即
(10)
由引理4、引理5,便得到五次有理PH插值曲线Φ(Z(t)),即
(11)
其中,α=Vi/a2或α=c2/Vf,Z(t)由(10)式确定。
4 最优插值形状的选取
对于“合理”的插值数据,由(9)式求出的a、b、c组成了满足插值数据的18组解,但由于PH曲线的内在特征及对称性,实际上得到的图形只有9条曲线,存在可以灵活处理拐点的曲线(如果不存在,可以通过改变初始数据使得这样的曲线存在),而其他插值曲线可能出现尖点、结点或明显不符合几何形状设计的需求,所以给出一个准则来选择通过PH曲线插值所得到的最优形状是非常重要的。本文采用文献[7]提出的“弹性弯曲能量”来选择五次有理PH曲线C2Hermite插值的最优形状,即
(12)
其中,κ为(Φ∘r(t))的曲率,即
5 数值实例
例1 给定C2Hermite数据来构造五次有理PH曲线C2Hermite插值曲线,即
按照上述算法,应用数学工具Matlab中的Slove求出关于a、b、c的所有18组复根分别为:
a=±2.010 3∓0.325 8i,∓1.429 4±0.762 6i,±0.492 5±1.142 1i,∓1.470 4±0.168 9i,±1.427 3∓1.011 8i,±0.643 7±0.333 6i,∓0.982 8∓1.138 8i,∓1.683 8±1.520 4i,±1.294 3∓1.467 2i;
b=∓8.638 4∓0.023 5i,±2.309 3∓1.562 6i,±3.969 0∓0.612 1i,±3.758 8 ±1.807 9i,∓0.904 8±2.545 9i,±0.454 4∓1.748 4i,∓4.906 4±4.073 2i,∓3.441 5∓6.429 8i,±2.932 7±1.992 9i;
c=±2.626 0±0.109 0i,±1.720 6±0.556 5i, ±0.848 7∓0.648 6i,±1.360 9∓0.501 9i, ±2.034 1∓0.127 6i,±1.932 9±0.417 2i, ±2.404 6∓0.174 2i,±2.428 3±0.591 7i, ±0.790 3±0.664 3i。
由此即可求出其余控制点Z1、Z2、Z3、Z4,分别将这些控制点及a、b、c带入(10)式,求出五次PHC2Hermite插值曲线Z(t),如图1所示。进一步将Z(t)带入(11)式,求出满足五次有理PH曲线C2Hermite插值曲线Φ(Z(t)),如图2所示。由(12)式分别可以求出Φ(Z(t))对应的9条PH曲线C2Hermite插值曲线的“弹性弯曲能量”,见表1所列。
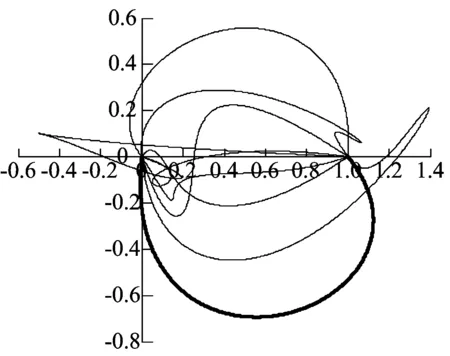
图1 五次PH C2Hermite插值曲线Z(t)
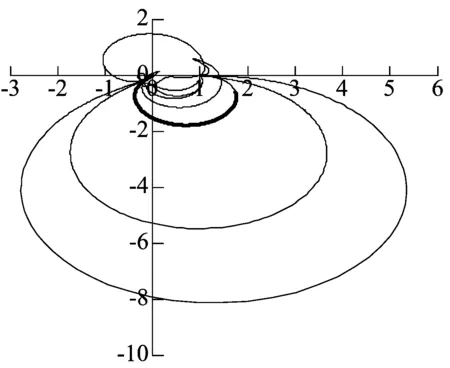
图2 五次有理PH曲线C2Hermite插值曲线Φ(Z(t))
表1 9条PH曲线C2Hermite插值曲线的弹性弯曲能量

曲线123456789弹性弯曲能量51 3326 861 6525 205 3242 54315 70138 691 33
由表1可以看出,第9条曲线的“弹性弯曲能量”最小,对应图2中的粗线,相应的五次PHC2Hermite插值曲线Z(t)对应图1中的粗线。
6 结束语
[1] Farouki R T,Sakkalis T.Pythagorean-hodograph[J].IBM Journal of Research and Development,1990,34(5):736-752.
[2] Farouki R T,Manjunathaiah J,Yuan G F.G codes for the specification of Pythagorean-hodograph tool paths and associated feedrate functions on open-architecture CNC machines[J].International Journal of Machine Tools and Manufacture,1999,39(1):123-142.
[3] Farouki R T,Shah S.Real-time CNC interpolators for Pythagorean-hodograph curves[J].Computer Aided Geometric Design,1996,13(7):583-600.
[4] Farouki R T,Manjunathaiah J,Nicholas D,et al.Variable-feedrate CNC interpolators for constant material removal rates along Pythagorean-hodograph curves[J].Computer-Aided Design,1998,30(8):631-640.
[5] Farouki R T,Neff C A.Hermite interpolation by Pythagorean hodograph quintics[J].Mathematics of Computation,1995,64(212):1589-1609.
[6] Farouki R T.The elastic bending energy of pythagorean-hodograph curves[J].Computer Aided Geometric Design,1996,13(3):227-241.
[7] Moon H P,Farouki R T,Choi H I.Construction and shape analysis of PH quintic Hermite interpolants[J].Computer Aided Geometric Design,2001,18(2):93-115.
[8] 陈国栋,王国瑾.五次 PH 曲线的 Hermite 插值[J].软件学报,2001,12(10):1569-1572.
[10] Farouki R T.The conformal mapz→z2of the hodograph plane[J].Computer Aided Geometric Design,1994,11(4):363-390.
[11] Ahlfors L V.Complex analysis:international series in pure and applied mathematics [M].3rded.New York,USA:McGraw-Hill,1978.
(责任编辑 张 镅)
DING Chen, TANG Shuo, LI Shao-hua, BAI Rui-feng
(School of Mathematics, Hefei University of Technology, Hefei 230009, China)
2013-12-17;
2014-02-25
国家自然科学基金资助项目(61272024); 安徽省自然科学基金资助项目(KJ2013B232)
丁 晨(1988-),男,安徽安庆人,合肥工业大学硕士生; 唐 烁(1964-),男,安徽巢湖人,合肥工业大学教授,硕士生导师.
10.3969/j.issn.1003-5060.2015.02.028
TP391.41
A
1003-5060(2015)02-0277-04
