张丽剑，罗跃生，张文平

（1.哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨150001；2.哈尔滨工程大学理学院，黑龙江哈尔滨150001）

变限积分的有限体积法解决对流扩散方程

张丽剑1，罗跃生2，张文平1

（1.哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨150001；2.哈尔滨工程大学理学院，黑龙江哈尔滨150001）

针对一维对流扩散方程，基于变限积分的有限体积法，提出一种高精度全离散方法。该方法在控制体内对方程进行变限积分，引入变限因子，然后分别对上下限再进行积分，从而将微分方程转化为积分方程，最后运用插值的方法对目标函数进行近似代替。该方法提高了计算精度，结果得到一维的收敛精度。采用Fourier分析法证明了格式为条件稳定。最后给出了非稳态和稳态2种情况下的数值算例，验证了所提出的格式具有高精度和易于编程计算的优点。

变限积分；高精度；对流-扩散方程；Fourier分析法；非稳态；一维

对流扩散方程在许多物理系统，特别是流体力学与传热学中有广泛的应用［1⁃3］。它描述的是诸如质量、热量、能量、涡度等的对流扩散的物理量的运动机理［4⁃11］。对于初边值条件一维对流扩散方程解析解的研究，几乎没有取得任何进展［1，4］。因此，很多的研究都致力于寻找对流扩散方程稳定的和相对精确的数值解［12⁃13，23⁃26］。近年，高阶紧致差分格式被用来求解方程的数值解［14⁃16，27］。格式最高具有四阶空间和时间精度［17⁃19，27］。本文提出了一种高精度全离散格式，其主要思想是将微分方程转化为积分方程来求解。

1 格式的构造

一维非稳态对流扩散方程：

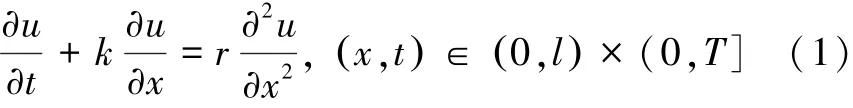
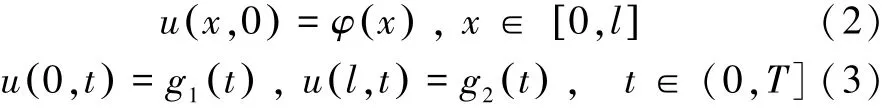
式中：（0，T］为时间域，φ、g1和g2均为已知的充分光滑函数，k和r分别为相速度和粘性系数，均为已知的常系数。

对于问题（1）～（3），本文首先将区域划分成M×N的网格，其中网格xi＝ih，i＝0，1，2，…，M，h＝l／M；tn＝nτ，n＝0，1，2，…，N，τ＝T／N。记u( ih，kτ)＝uni表示函数u在网格(ih，kτ)上的值。

在控制区域Ω＝[y1，y2]×[tn，tn+1]内，首先运用有限体积法思想对方程（1）两边作变限积分，其中y1，y2∈(0，l)，最后得到化简式：

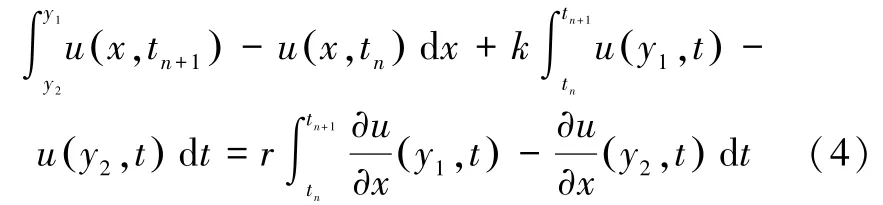
然后在上下限的控制区域Ω′＝[xi-ε2，xi]× [xi，xi+ε1]内，分别对方程（4）两边进行积分：

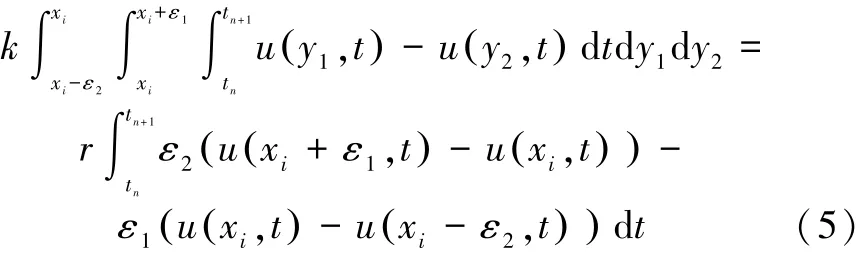
式中：ε1、ε2分别为控制上下限积分区域大小的变限因子。式（5）中，沿x方向上的积分区域如图1所示。

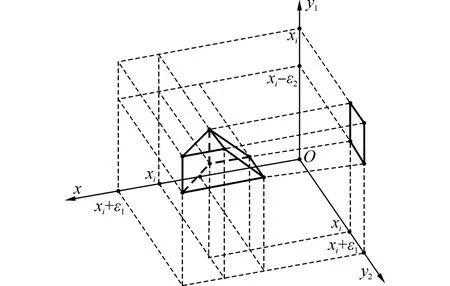
图1 沿x方向上的积分区域Fig.1 The domain of integration of the proposed for⁃mat about x direction

通过上述积分，将微分方程（1）转化为积分方程（5），于是用二元六点拉格朗日插值法，对u x，t()进行插值。整理并舍去小项，可得方程（1）的全离散格式：

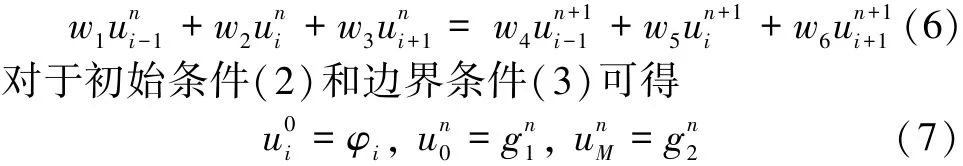
则式（6）、（7）即为问题（1）～（3）的全离散格式。

2 精度估计

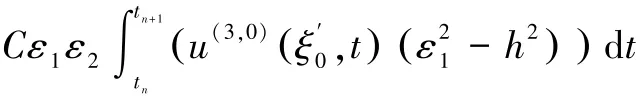
由于在对方程（1）进行离散时，一共对x进行了3次积分，对t进行了1次积分，则等式两边应除以h3τ，从而可得离散格式（6）的截断误差为O h4／τ+h3+hτ+τ2／h+τ3／h2

( )，显然，该截断误差大于二阶。

3 稳定性分析

假设边界条件精确满足，采用Fourier分析法对全离散格式进行稳定性分析，用μ表示计算u时产生的误差，代入离散格式（6），则满足齐次方程：

显然可得G′1

2≤G′22，即G2≤1，由此当ε1≥ε2时可得全离散格式稳定。

4 算法分析

基于变限积分的有限体积法是在有限体积法的基础上提出的新算法，该方法结合了有限元和有限差分法的思想，同时又继承了有限体积法的优点。

该算法首先对整体计算域进行控制区域的划分，然后对目标方程在局部控制区域内进行变限积分。将微分方程完全转化为积分方程，使其消除偏导数影响。最后，选择关于网格点的插值多项式对积分方程中的被积函数进行插值，从而得到一组含有变限因子ε的全离散格式。

该方法相较于有限差分法，明显提高了网格剖分的灵活性，使其能够适用于非规则网格。能够通过选取高精度的插值多项式来提高离散格式的精度。通过选取不同的ε，使得在达到同样精度的条件下，得到的全离散格式满足某种较好的性质。本文算法的优势主要体现在如下3个方面：

1）关于积分区域的选取。在对目标方程进行变限积分时，能够以非规则网格区域为积分区域进行积分。这是网格剖分灵活性的体现。

2）关于变限因子ε的选取。选取不同的ε可得到不同的离散格式，从而能够有目的地挑选其中满足某种性质的离散格式，例如稳定性。通过选取不同的ε，达到的计算效果也会有所不同。

3）关于插值多项式的选取。选取不同精度的插值多项式进行插值能够直接影响离散格式的精度，因此，使用该方法能在理论上达到任意精度。甚至还能够使用2种以上的插值多项式进行加权混合使用。

5 数值算例

对流扩散问题包含非稳态和稳态情况，下面运用本文离散格式分别对非稳态和稳态对流扩散方程进行数值实验。

5.1 非稳态情况

考虑一维非稳态对流扩散方程，利用格式（6），解决如下初边值问题：

其定态解析解为：u x，t()＝e5x-4t，方程的初边值条件由解析解中得到。

于是，令L＝1，T＝1，用本文所提出的新算法对于不同的步长h和τ进行试算，可得结果如表1。从表1中能够得到，随着步长h和τ的减少，L2模误差逐渐减小。变限因子ε1和ε2对实际计算结果有很大的影响，因此在表2中，在取定h和τ时，选取不同的变限因子进行误差比较。rate为收敛阶。

表1 ε1＝ε2＝h／2 000时的误差比较Table1 The error comparison when ε1＝ε2＝h／2 000

表2 h＝τ＝0.01时的误差比较Table2 The error comparison when h＝τ＝0.01

图2 h＝τ＝0.01，不同ε1、ε2时的解析解和数值解Fig.2 The analytical and numerical solu⁃tions of different ε1，ε2，h＝τ＝0.01

图3 h＝τ＝0.005，T＝5，ε1＝ε2＝h／240时的解析解和数值解Fig.3 The analytical and numerical solutions，h＝τ＝0.005，T＝5，ε1＝ε2＝h／240

图2 为取时间步长h和空间步长τ均为0.01，取T＝1，取不同变限因子ε1、ε2，将解析解和数值解进行比较。图3为取时间步长h和空间步长τ均为0.005，取T＝5，取变限因子ε1＝ε2＝h／240，将解析解和数值解进行比较。

图4为取时间步长h和空间步长τ均为0.005，取变限因子ε1＝ε2＝h／240时，绝对误差随时间变化趋势。从图中可知，误差主要集中在边界。

图4 h＝τ＝0.005，ε1＝ε2＝h／240，绝对误差随时间变化Fig.4 The absolute value of error changing with time，h＝τ＝0.005，ε1＝ε2＝h／240

计算结果表明，式（6）满足理论精度。随着时间的推移，数值解和解析解之间的绝对误差逐渐减小，符合之前的证明分析。

5.2 稳态情况

考虑一维稳态对流扩散方程，利用格式（6），解决如下边值问题：

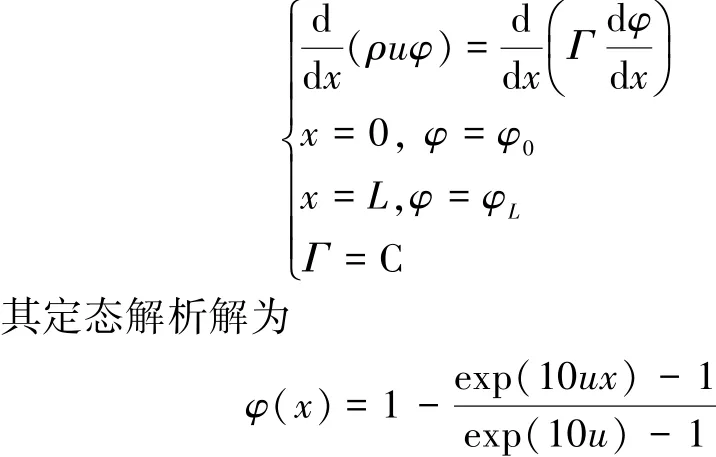
5.2.1 流速u＝0.1 m／s，h＝0.2 m

由u＝0.1 m／s，h＝0.2 m，ρ＝1.0 kg／m3，Γ＝0.1 kg／（m·s），取ε1＝ε2时，得到离散方程组：

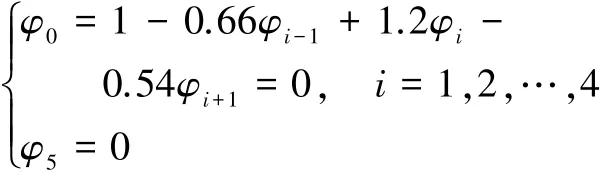
此时：

对离散方程组进行求解，结果列于表3中，传统格式是指二阶中心差分格式，由解可以看出，所求得的结果在物理上是真实的。

表3 u＝0.1 m／s，h＝0.2 m时，解析解、数值解与相对误差Table3 Analytical solutions，numerical solutions and rela⁃tive error，u＝0.1 m／s，h＝0.2 m

5.2.2 流速u＝2 m／s，h＝0.2 m

求解过程5.2.1中的其他条件不变，流速由0.1 m／s提高到2 m／s。此时：

得到离散方程组：

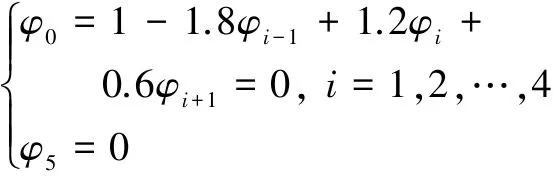
表4 u＝2 m／s，h＝0.2 m时，解析解、数值解与相对误差Table4 Analytical solutions，numerical solutions and rela⁃tive error，u＝2 m／s，h＝0.2 m

对离散方程组进行求解，结果列于表4中，传统格式是指二阶中心差分格式，由解可以看出，所求得的结果在物理上是不真实的，出现了振荡。求解过程5.2.2节与求解过程5.2.1节相比较，只提高了流速，其他任何条件都未改变。

5.2.3 流速u＝2 m／s，h＝0.05 m

求解过程5.2.2节中的其他条件不变，加密网格。此时：

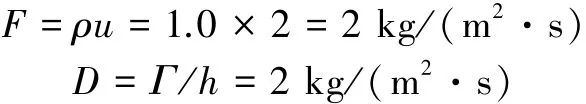
得到离散方程组：

对离散方程组进行求解，结果列于表5中，可见，求解过程5.2.2节中出现解的振荡；求解过程5.2.3节中只是加密了网格，又得到了物理上真实的解。

表5 u＝2 m／s，h＝0.05 m时，解析解、数值解与相对误差Table5 Analytical solutions，numerical solutions and rela⁃tive error，u＝2 m／s，h＝0.05 m

5.2.4 结果分析

在求解过程5.2.1中F／D＝0.1／0.5＝0.2；求解过程5.2.2中F／D＝2／0.5＝4；在求解过程5.2.3中F／D＝2／2＝1，见表5。传统格式是指二阶中心差分格式，可见在F／D较大时可能出现解的不真实，本文格式比传统格式精度提高了许多。

6 结束语

本文针对一维对流扩散方程，并以一维非稳态方程为例，基于变限积分的有限体积法，建立了一维的新的高精度数值离散格式，其精度能够达到O h4／τ+h3+hτ+τ2／h+τ3／h2

( )，利用Fourier分析法对全离散格式进行了稳定性分析，发现所构造的格式能在变限因子ε1≥ε2条件下能够达到稳定，通过数值算例证实了上述结论。ε的选取目前只是通过实验获得的经验，还需要进一步总结和证明理论上的规则。本文在理论上给出了离散格式构造的方法以及精度估计和稳定性分析的证明，通过算例验证对工程实际有借鉴意义。进一步研究本课题将对高精度离散格式的构造具有重大意义。

［1］DEHGHAN M.Weighted finite difference techniques for the one⁃dimensional advection diffusion equation［J］.Appl Math Comput，2004，147：307⁃319.

［2］ROACHE P J.Computational fluid dynamics［M］.Hermosa Publishers，1972.

［3］SPALDING D B.A novel finite difference formulation for dif⁃ferential expressions involving both first and second deriva⁃tives［J］.International Journal for Numerical Methods in En⁃gineering，1972，4（4）：551⁃559.

［4］DEHGHAN M.Numerical solution of the three⁃dimensional advection⁃diffusion equation［J］.Applied Mathematics and Computation，2004，150（1）：5⁃19.

［5］ISENBERG J，GUTFINGER C.Heat transfer to a draining film［J］.International Journal of Heat and Mass Transfer，1973，16（2）：505⁃512.

［6］PARLANGE J Y.Water transport in soils［J］.Annual Re⁃view of Fluid Mechanics，1980，12（1）：77⁃102.

［7］FATTAH Q N，HOOPES J A.Dispersion in anisotropic，homogeneous，porous media［J］.Journal of Hydraulic Engi⁃neering，1985，111（5）：810⁃827.

［8］CHATWIN P C，ALLEN C M.Mathematical models of dis⁃persion in rivers and estuaries［J］.Annual Review of Fluid Mechanics，1985，17（1）：119⁃149.

［9］HOLLY J R F M，USSEGLIO⁃POLATERA J M.Dispersion simulation in two⁃dimensional tidal flow［J］.Journal of Hy⁃draulic Engineering，1984，110（7）：905⁃926.

［10］KUMAR N.Unsteady flow against dispersion in finite por⁃ous media［J］.Journal of Hydrology，1983，63（3）：345⁃358.

［11］GUVANASEN V，VOLKER R E.Numerical solutions for solute transport in unconfined aquifers［J］.International Journal for Numerical Methods in Fluids，1983，3（2）：103⁃123.

［12］KARAHAN H.Unconditional stable explicit finite differ⁃ence technique for the advection⁃diffusion equation using spreadsheets［J］.Advances in Engineering Software，2007，38（2）：80⁃86.

［13］KARAHAN H.Implicit finite difference techniques for the advection⁃diffusion equation using spreadsheets［J］.Ad⁃vances in Engineering Software，2006，37（9）：601⁃608.

［14］SUN H，ZHANG J.A high⁃order compact boundary value method for solving one⁃dimensional heat equations［J］.Nu⁃merical Methods for Partial Differential Equations，2003，19（6）：846⁃857.

［15］TIAN Z F.A rational high⁃order compact ADI method for unsteady convection⁃diffusion equations［J］.Computer Physics Communications，2011，182（3）：649⁃662.

［16］HIRSH R S.Higher order accurate difference solutions of fluid mechanics problems by a compact differencing tech⁃nique［J］.Journal of Computational Physics，1975，19（1）：90⁃109.

［17］CIMENT M，LEVENTHAL S H，WEINBERG B C.The op⁃erator compact implicit method for parabolic equations［J］.Journal of Computational Physics，1978，28（2）：135⁃166.［18］BAZAN F S V.Chebyshev pseudospectral method for com⁃ puting numerical solution of convection⁃diffusion equation［J］.Applied Mathematics and Computation，2008，200（2）：537⁃546.

［19］MOHEBBI A，DEHGHAN M.High⁃order compact solution of the one⁃dimensional heat and advection⁃diffusion equa⁃tions［J］.Applied Mathematical Modelling，2010，34（10）：3071⁃3084.

［20］DEHGHAN M.Implicit collocation technique for heat equa⁃tion with non⁃classic initial condition［J］.International Journal of Nonlinear Sciences and Numerical Simulation，2006，7（4）：461⁃466.

［21］KARAA S，ZHANG J.High order ADI method for solving unsteady convection⁃diffusion problems［J］.Journal of Computational Physics，2004，198（1）：1⁃9.

［22］TIAN Z F，GE Y B.A fourth⁃order compact ADI method for solving two⁃dimensional unsteady convection⁃diffusion problems［J］.Journal of Computational and Applied Mathe⁃matics，2007，198（1）：268⁃286.

［23］王红梅.对流扩散方程的特征有限元方法［D］.济南：山东大学，2012.WANG Hongmei.Characteristics finite element methods for convection⁃diffusion problems［D］.Jinan：Shandong Uni⁃versity，2012.

［24］丁晓燕，冯秀芳.求解二维非定常对流扩散方程的高精度指数型差分方法［J］.宁夏大学学报：自然科学版，2014，35（1）：6⁃13.DING Xiaoyan，FENG Xiufang.A high⁃order exponential method for solving unsteady convection⁃diffusion equation［J］.Journal of Ningxia University：Natural Science Edi⁃tion，2014，35（1）：6⁃13.

［25］秦新强，王志刚，王全九，等.对流占优扩散方程的楔形基无网格法［J］.工程数学学报，2013，30（5）：721⁃730.QIN Xinqiang，WANG Zhigang，WANG Quanjiu，et al.Meshless method with ridge basis functions for convection⁃dominated diffusion equations［J］.Chinese Journal of Engi⁃neering Mathematics，2013，30（5）：721⁃730.

［26］马亮亮.变系数空间分数阶对流⁃扩散方程的有限差分解法［J］.沈阳大学学报：自然科学版，2013，25（4）：341⁃344.MA Liangliang.Finite difference methods for space fraction⁃al convection⁃diffusion equation with variable coefficients［J］.Journal of Shenyang University：Natural Science，2013，25（4）：341⁃344.

［27］杨录峰，李春光.一种求解对流扩散反应方程的高阶紧致差分格式［J］.宁夏大学学报：自然科学版，2013，34（2）：101⁃104.YANG Lufeng，LI Chunguang.A high⁃order compact finite difference scheme for solving the convection diffusion reac⁃tion equations［J］.Journal of Ningxia University：Natural Science Edition，2013，34（2）：101⁃104.

Solving convection⁃diffusion equation by using the finite volume method with variable limit integral

ZHANG Lijian1，LUO Yuesheng2，ZHANG Wenping1
（1.College of Power and Energy Engineering，Harbin Engineering University，Harbin 150001，China；2.College of Science，Harbin Engineering University，Harbin 150001，China）

In this paper，the one⁃dimensional convection⁃diffusion equation using one⁃dimensional unsteady equations as an example figures out a new high precision fully discrete format that is based on the finite volume method with variable limit integral.This method first integrates the equation with variable limit integral in the control body and introduces a variable limit integral factor.After that it integrates the upper and lower limits to transform the differential equation into the integral equation and then uses the interpolation method to approximately replace the objective function.In this way，the accuracy of the diffusion term is improved，deriving the one⁃dimensional convergence precision.The Fourier analysis method is used to prove the conditional stability of formation.Finally，the numerical examples of non⁃stable and stable conditions are given to verify the advantages of high accuracy and the easiness of programming calculation.

variable limit integral；high precision；convection diffusion model；Fourier analysis；unsteady state；one⁃dimensional

10.3969／j.issn.1006⁃7043.201410049

http：／／www.cnki.net／kcms／detail／23.1390.U.20150309.1453.002.html

O551

A

1006⁃7043（2015）03⁃0427⁃05

2014⁃10⁃20.网络出版时间：2015⁃03⁃09.

国家自然科学基金资助项目（51206031，51479038）.

张丽剑（1979⁃），女，讲师，博士研究生；罗跃生（1960⁃），男，教授，博士生导师；张文平（1956⁃），男，教授，博士生导师.

张丽剑，E⁃mail：756778282＠qq.com.