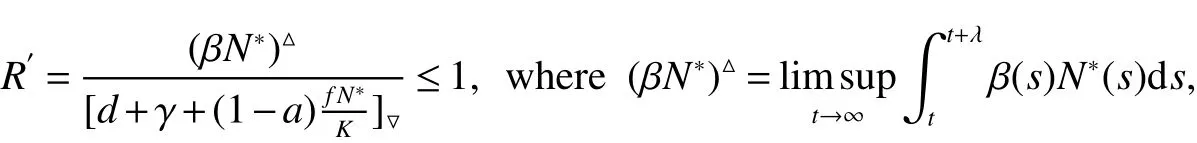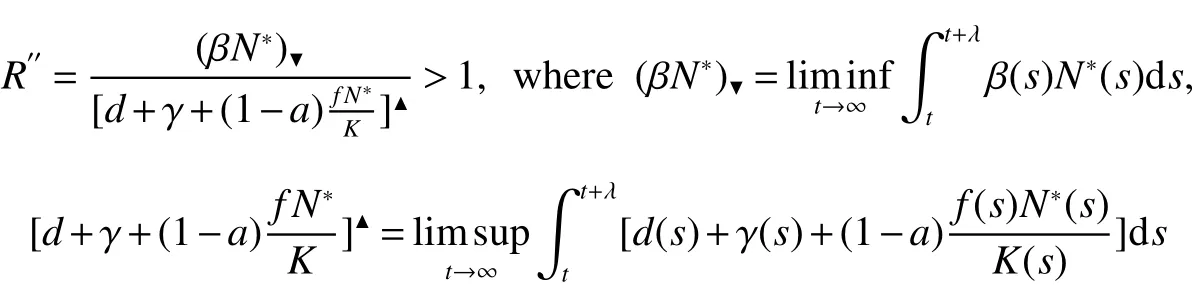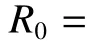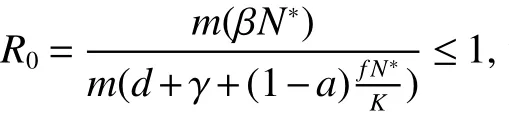Permanence and Extinction for Nonautonomous SIRS Epidemic Model with Density Dependence∗
2015-05-16XUMingxingTENGZhidongZHANGLong
XU Ming-xing,TENG Zhi-dong,ZHANG Long
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
0 Introduction
As is well known,the research on the epidemic dynamical models is a very important subject in the mathematical theory of epidemiology.Various epidemic dynamical models have been proposed and analyzed,and great progress has been achieved[1–5].Particularly,the autonomous epidemic models have been investigated extensively in recent years.Many important and interesting results are established.These results come down to the computation of threshold value and basic reproduction number,the local and global stability of the disease-free equilibrium and endemic equilibrium,the existence of periotic orbits,the persistence and extinction of the disease,the existence of backward bifurcation,etc.And many results have been applied successfully to solve the practical medicinal problems.
However,the nonautonomous phenomenon often occurs in many realistic epidemic models.It will be more identical with the sound background as we consider long-term dynamical behavior of an epidemic model,the parameters of the model usually will change with time.Therefore,the research on the nonautonomous epidemic models also plays very important role in epidemiology.We see that there have been some research works on the nonautonomous epidemic models[6,7].Particularly,the works in allusion with density dependent epidemic models can be found in[8–10]and the references cited therein.
In this paper we consider the following nonautonomous SIRS epidemic model,
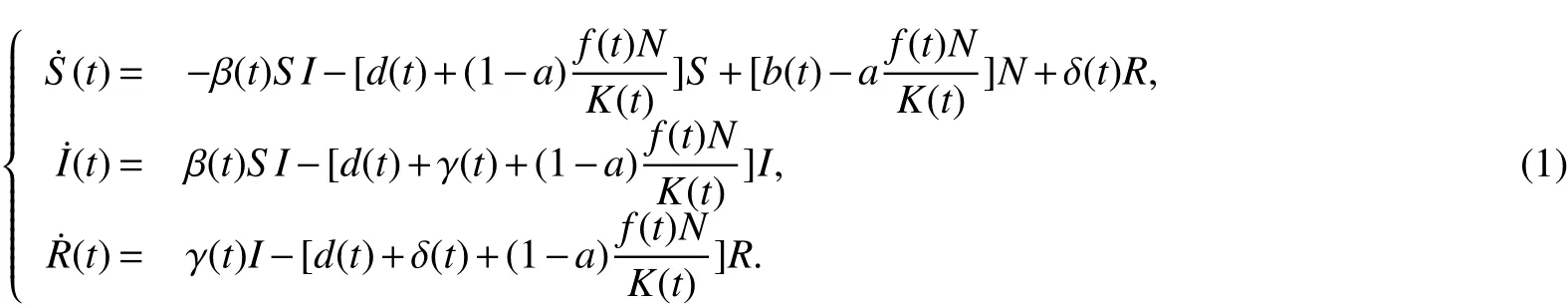
Our purpose is to study the extinction and permanence of the disease for model(1).We will give some new threshold valuesWe will prove that the disease is extinct if≤0 or<0,and permanent if>0.When model(1)degenerates into periodic or almost periodic case,the basic reproduction numberR0is obtained,andR0acts as a sharp threshold for the extinction and permanence of the disease.
This paper is organized as follows.Section 1 contains some basic preliminaries including hypotheses,some lammas,the de finition of extinction,permanence of disease.The extinction of the disease is settled in Section 2.Section 3 deals with the permanence of the disease.In Section 4,we conclude some corollaries.
1 Preliminaries
In model(1),S(t),I(t)andR(t)denote the size of susceptible,infectious and recovered at timet,respectively,N(t)=S(t)+I(t)+R(t),β(t)denotes the disease transmission coefficient,b(t)andd(t)are the natural birth and death rates at timet,γ(t)and δ(t)are the instantaneous per capita rates of leaving the infection stage and removed stage at timet.f(t)=b(t)−d(t)is the intrinsic growth rate at timet,andK(t)is the carrying capacity of the population at timet,wherea∈[0,1].
For a bounded functionh(t)de fined onR+=[0,+∞),we denotehΛ=supt≥0h(t),hλ=inft≥0h(t).The initial condition for any solution of model(1)is given in the following form

InfectiveIis said to be extinct,if limt→∞I(t)=0 for any solution(S(t),I(t),R(t))of model(1)with initial value(2).InfectiveIis said to be permanent,if there are positive constants ν1,ν2such that
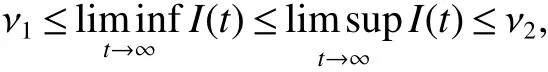
for any solution(S(t),I(t),R(t))of model(1)with initial value(2).
For model(1),we introduce the following assumptions.
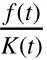
(H2)There are positive constants ω1,ω2,ω3,ω4such that
Remark 1When model(1)degenerates into ω-periodic case,that is,β(t),γ(t),b(t),K(t),d(t),f(t),δ(t)are nonnegative continuous periodic functions with period ω>0,then(H2)degenerates into
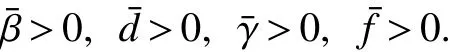
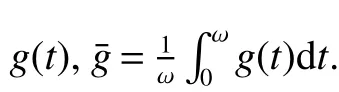
When model(1)degenerates into almost periodic system,that is,β(t),γ(t),b(t),K(t),d(t),f(t)and δ(t)are nonnegative continuous almost periodic functions,then(H2)degenerates into
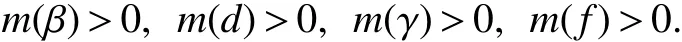
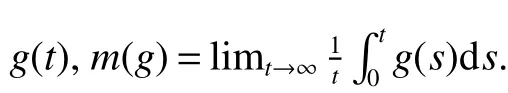
Consider the well-known nonautonomous logistic equation

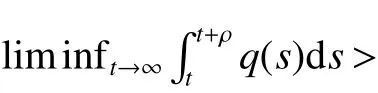
Lemma 1(a).There is a constantM0>0 such that for any positive solutionz(t)of equation(3),limsupt→∞z(t)≤.
(d).Each fixed positive solutionz(t)of equation(3)is globally uniformly attractive.
(e).When equation(3)is ω-periodic,>0 and>0,then equation(3)has a unique globally asymptotically stable positive ω-periodic solution.
(f).When equation(3)is ω-periodic,≤0 and>0,then for any positive solutionz(t)of equation(3),
(g).When equation(3)is almost periodic,m(p)>0 andm(q)>0,then equation(3)has a unique globally asymptotically stable positive almost periodic solution.
(h).When equation(3)is almost periodic,m(p)≤0 andm(q)>0,then for any positive solutionz(t)of equation(3),
Next,we consider the following nonautonomous linear equation

We have the following result.
Lemma 2If there are constants η>0 and γ >0 such that

then any solutions of equation(4)with positive initial value are ultimately bounded.
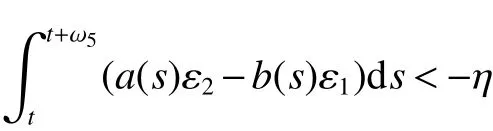
for allt≥T,and for any constantH>0,there is aP>0 such that for any α ≥Pandt≥ 0

LetN(t)=S(t)+I(t)+R(t),then model(1)becomes into the following form
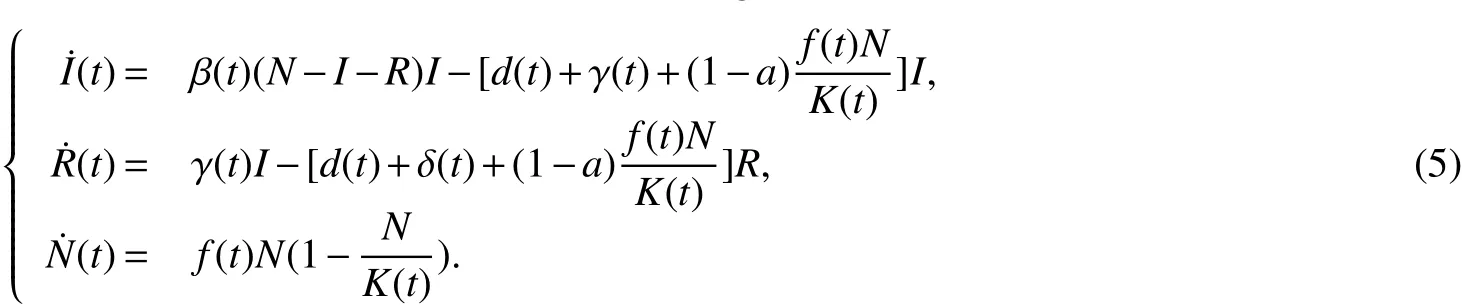
Lemma 4Suppose that(H1),(H2)hold.Then any solution(N(t),I(t),R(t))of model(5)with initial condition(2)is nonnegative and bounded onR+.
The proofs of Lemmas 1-4 are not hard,here we hence omit them.
2 Extinction
In model(1),total populationN(t)satis fies the following equation

From Lemma 1,there are positive constantsmandMsuch that for any positive solutionN(t)of equation(6),m≤liminft→∞N(t) whereN∗(t)be some fixed solution of equation(6)with initial valueN∗(0)>0.We first give the following extinction theorem. Theorem 1Suppose that(H1)and(H2)hold,if there is a constant λ>0 such that then infectiveIin model(1)is extinct. ProofFirstly,we prove thatR∗0is independent of the choice ofN∗(t).In fact,Lemma 1(d)implies that for any ε>0 small enough and any solutionN(t)of equation(6)with initial valueN(0)>0 there exists aT≥0 such that ast≥T,N∗(t)−ε≤N(t)≤N∗(t)+ε.Hence,for allt≥T, and If≤ 0 hold,from the first equation of model(5),we have From(7),by Lemma 1(c),using the comparison theorem we can obtain that limt→∞I(t)=0. From the first equation of model(5),we have Integrating from 0 tot,we have From(8)and(9)we finally have limt→∞I(t)=0.This completes the proof. Theorem 2Suppose that(H1)and(H2)hold,if there is a constant λ>0 such that then infectiveIin model(1)is permanent. LetM1andM2are I(t)and R(t)’s limsup. From(H1),(H2)and Lemma 3,choose constants ε1>0,ε2>0,T1>0 and η2>0 such that for allt≥T1,wherek=1+γΛω2.Firstly,we claim that If it is not true,then there existsT2>T1such thatI(t)<ε1for allt≥T2.Suppose thatR(t)≥ε2fort≥T2,then from the second equation of model(5),we have for allt≥T2.From(10)it follows limt→∞R(t)= −∞,which is a contradiction.Hence,there is a τ1≥T2such thatR(τ1)<ε2.Now,we prove fort≥ τ1.If it is not true,then there is a τ2> τ1satisfyingR(τ2)> ε2+γΛω2ε1.Hence,there is a τ3∈ (τ1,τ2)such thatR(τ3)= ε2andR(t)> ε2fort∈ (τ3,τ2).Choose an integerp≥ 0 such that τ2∈ [τ3+pω2,τ3+(p+1)ω2).Integrating the second equation of model(5)from τ3to τ2,and using(10),we obtain This is a contradiction.Hence,(14)is true. From the first equation of model(5),we have for allt≥ τ1.Integrating from τ1tot,we have From(11),it follows limt→∞I(t)=+∞.This is a contradiction.Hence,(13)is true. Secondly,we prove that there is a constant ν1>0 such that From(10)-(12),Lemma 3 and(H2),there existP>0 and η3>0 such that for any α ≥Pandt≥ 0.Choose an integerC>0 large enough such that for anyt≥ 0 and ξ0∈ [0,P).From(13),there are only two possibilities as follows (1)I(t)≥ ε1for all larget;(2)I(t)oscillates about ε1for all larget. We will show thatI(t)≥ε1exp(−L(C+2)P),ν1astis large sufficiently,whereEvidently,we only need to consider case(2).Lett1andt2be sufficiently large such that Ift2−t1≤(C+2)P,then from the first equation of model(5)and using Lemma 4,we obtain which impliesI(t)≥ε1exp(−L(C+2)P)for allt∈[t1,t2]. Ift2−t1>(C+2)P,then from(19),we haveI(t)≥ε1exp(−L(C+2)P)for allt∈ [t1,t1+(C+2)P].IfR(t)≥ε2for allt∈[t1,t1+P],then integrating the second equation in model(5)fromt1tot1+P,and using(16),we obtain This is a contradiction.Hence,there is at∗∈ [t1,t1+P]such thatR(t∗)< ε2.From(14),we can obtain for allt∈ [t∗,t2].Obviously,ast∈ [t1,t1+2P],by(19),we obtain We claim thatI(t)≥ν1for allt∈[t1+(C+2)P,t2].If it is not true,then there is at0=t1+(C+2)P+T0,such atI(t0)=ν1andI(t)≥ν1on[t1,t0],whereT0=nP+ξ≥0,n≥0 is an integer,ξ∈[0,P). From the first equation of model(5)and(20),we have for allt∈[t1+2P,t2].Integrating fromt1+2Ptot0and using(17),(18),we further have This is a contradiction.So,I(t)≥ ν1for allt∈[t1,t2].Hence,liminft→∞I(t)≥ ν1.From Lemma 4,we finally have that infectiveIis permanent.This completes the proof. As applications of Theorems 1 and 2,we have the following corollaries. Corollary 1Suppose that(H1)and(H2)hold and there is a constant λ>0 such that andN∗(t)is some fixed solution of equation(6)withN∗(0)>0.Then infectiveIis extinct. Corollary 2Suppose that(H1)and(H2)hold and there is a constant λ>0 such that andN∗(t)is some fixed solution of equation(6)withN∗(0)>0.Then infectiveIis permanent. Corollary 4Suppose that model(1)is periodic,(H1)and(H2)hold.Then infectiveIis permanent if and only ifR0>1. Corollary 6Suppose that model(1)is almost periodic,(H1)and(H2)hold.Then infectiveIis permanent if and only ifR0>1. References: [1]Hethcote H W.Oscillations in endemic model for pertussis[J].Canad Appl Math Quart,1998,6:61-88. [2]Brauer F.Backward bifurcations in simple vaccination models[J].J Math Anal Appl,2004,298:418-431. [3]Moghadas S M.Analysis of an epidemic model with bistable equilibria using the poincar index[J].Appl Math Comp,2004,149:689-702. [4]Allen L J S,Burgin A.Comparision of deterministic and stochastic SIS and SIR models in discrete time[J].Math Biosci,2000,163:1-33. [5]Moghadas S M.Modelling the effect of imperfect vaccines on disease epidemiology[J].Discr Cont Dyn Syst,2004,4:999-1012. [6]Thieme H R.Uniform persistence and permanence for nonautonomous semi fl ows in population biology[J].Math Biosci,2000,166(2):173-201. [7]TengZ,LiuY,ZhangL.PersistenceandextinctionofdiseaseinnonautonomousSIRSepidemicmodelswithdisease-inducedmortality[J].Nonlinear Anal,2008,69:2599-2614. [8]LiuJ,ZhangT.Analysisofanonautonomousepidemicmodelwithdensitydependentbirthrate[J].AppliedMathematicalModelling,2010,34:866-877. [9]Yoshida N,Hara T.Global stability of a delayed SIR epidemic model with density dependent birth and death rates[J].J Comput Appl Math,2007,201:339-347. [10]Song M,Ma W,Takeuchi Y.Permanence of a delayed SIR epidemic model with density dependent birth rate[J].J Comput Appl Math,2007,201(2):389-394. [11]TengZ,ChenL.Permanenceandextinctionofperiodicpredator-preysystemsinapatchyenvironmentwithdelay[J].NonlinearAnal.:RWA,2003,4:335-364.
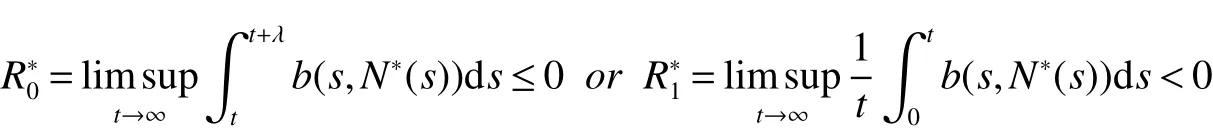




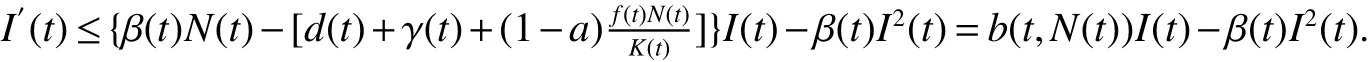


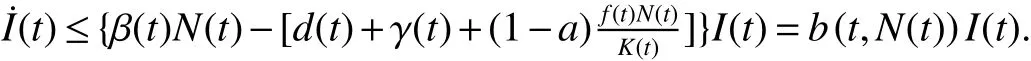

3 Permanence

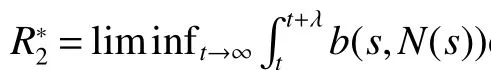
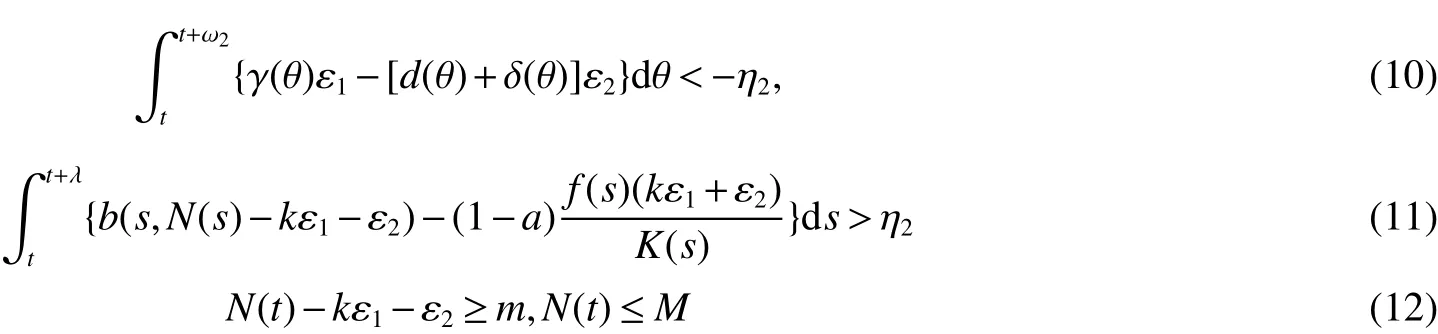

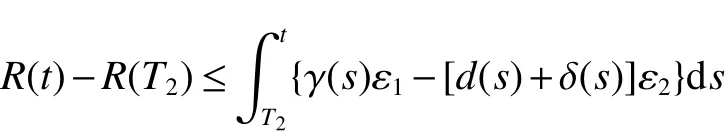

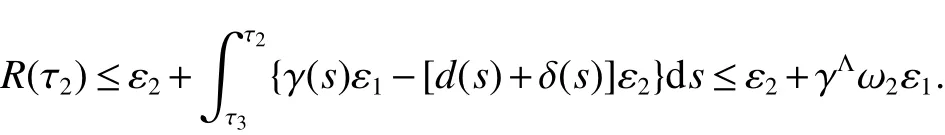
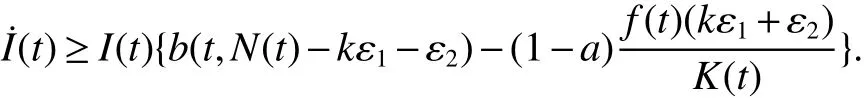
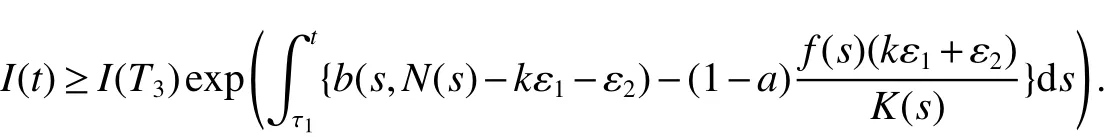


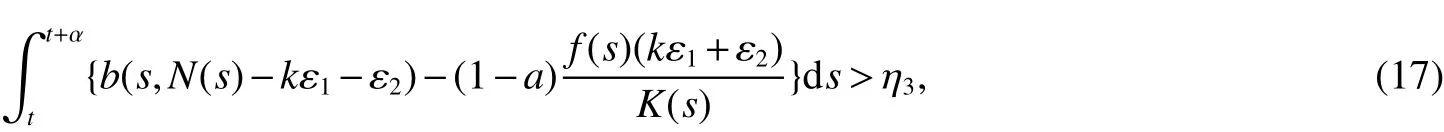
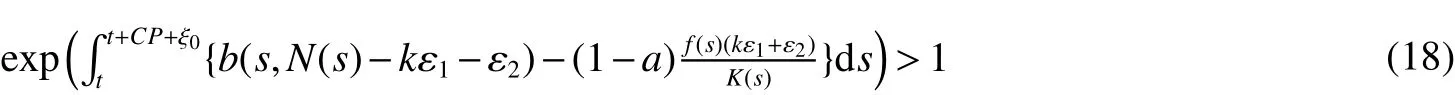
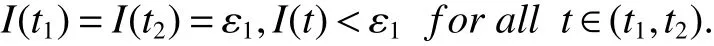





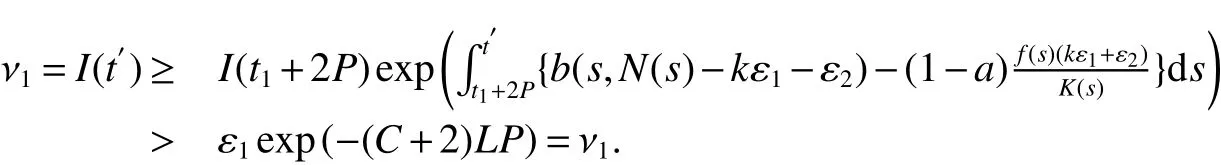
4 Some corollaries