王晓敏，赵喜杨，姚 兵

（西北师范大学 数学与统计学院，甘肃 兰州 730070）

0 引 言

现实世界中的自然、社会和科学系统均以网络的形式存在，而且这些网络大多数具有无标度性或小世界性，或者二者皆有［1－3］.当今的复杂网络理论已成为很多学科发展的新视角和指导思想，如疾病传播［4］.近年来一个活跃的研究课题是试图运用生成树来刻画复杂网络，从生成树这一全新的视角出发，对复杂网络的拓扑结构、物理意义和数学特性进行深入、广泛的研究.新方法已在金融、生理医学、生物等自然科学或社会科学领域得到深入浅出的探讨.

通常，复杂网络中含有很多的叶子，所以在网络的结构研究中自然而然地使用了生成树，使得生成树能够广泛地用于网络研究.例如，无线传感器网络的生成树最大限度地提高了链路的质量度量的总和，并提供了与所有节点对之间的最短的最弱链路的路径［5］.生成树的最典型的应用之一是：Perlman［6］利用生成树与网络间的结构关系发明了广泛用于网桥、交换机上的生成树协议，以及各种使用路由算法的链路状态机制.应用生成树在复杂网络中实现有效的搜索也是研究网络的一个重要的课题.例如：生成树被应用于网络的搜索算法［5］.复杂网络搜索的早期例子：著名的“六度分离”实验在一定程度上揭示了实际网络的可搜索性.Kleinberg［7］首先在理论上研究了复杂网络的搜索能力，即在网络中实现快速搜索的性质；之后Kleinberg、Watts、Adamic等［8］针对各自的特定模型提出了对应的搜索算法.值得注意的是，关于无标度生成树的研究报道很少［9］，理解或给出网络模型的无标度生成树的文章几乎见不到.

为更好地理解和认识复杂网络，学者们经常采用建立动态网络模型来逼近和模拟现实网络.本文借用相似于文献［3］的构造网络模型的方法，采用初始网络为一般的连通网络，并使得新进入网络的节点多于一个，从而构造出本文的研究对象SBEGN 模型.不难观察到，新发表的文章更倾向于引用一些被广泛引用的重要文献，新的个人主页上的超文本链接更有可能指向著名的站点，与强者恒强、弱者恒弱的网络现象相吻合.受这些网络现象的启发，本文设计时间优先层次搜索算法来寻找具有最多叶子的生成树，以期用算法优化研究网络的生成树，提高网络的搜索效率，减少网络的运算量，为寻找实际网络模型的生成树提供理论帮助.本文所考虑的图均为有限、无向简单图，没有定义的术语和符号均源于文献［10］.对于一个图G，它的叶子节点的集合用记号L（G）表示，nd（G）表示图G中度数为d的顶点的个数.记号｜X｜表示集合X的元素个数.

1 SBEGN模型的建立及其基本性质

对任意给定的至少有2 个节点的连通网络N（0），用d1，d2，…，da表示连通网络N（0）不同的度，且 满 足d1＞d2＞… ＞da.初 始 网 络 为N（0），用记号nv（0）和ne（0）分别表示它的节点个数和边数目，记号V（0）和E（0）分别表示初始网络N（0）的节点集合和边集合，使得nv（0）＝｜V（0）｜，ne（0）＝｜E（0）｜.对于初始网络N（0）的每一条边界边uv∈E（0），新增加m个节点，并且将这m个节点与边uv的端点u、v分别相连，产生t＝1时刻的网络N（1），并将最后一个新节点w与节点u、v分别相连所得的2条边wu和wv定义为网络N（1）的边界边.记号X1代表给N（0）新增加的节点集合，Y1代表给N（0）新增加的边集合，则有Y1＝｛wu，wv：uv∈E（0），w∈X1｝，以及V（1）＝V（0）∪X1，E（1）＝E（0）∪Y1，｜Y1｜＝2｜X1｜＝2mne（0）.

类似地，对于网络N（1）的每条边界边xy∈E（1），新增加m个新节点，并且将这m个节点分别与边xy的端点x、y相连，从而得到t＝2时刻的网络N（2），并将最后一个新节点z与节点x、y分别相连所得的2 条边zx和zy定义为网络N（2）的边界边.显然，N（2）的节点集合可表示为V（2）＝V（1）∪X2，它的边集合为E（2）＝E（1）∪Y2.以此类推，按照上述构造方法，从网络N（t－1）可得到网络N（t），简称它为SBEGN 模型.下面给出SBEGN 模型N（t）的一些基本参数.记号Xk和Yk分别表示给N（k－1）新增的节点集合和边集合.当t≥1时，SBEGN 模型N（t）的节点集合V（t）与边集合E（t）可以分别表示为

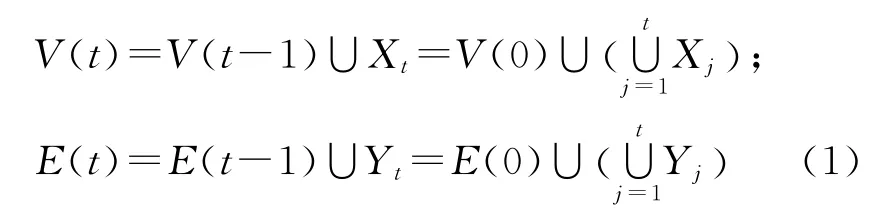
因为

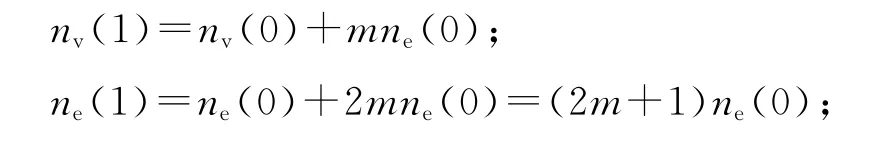
不难得到SBEGN 模型N（t）的节点数目和边数目

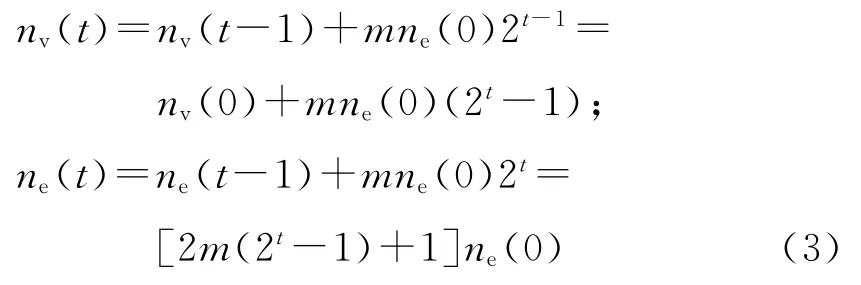
此外，SBEGN 模型N（k）的新增加节点数目为

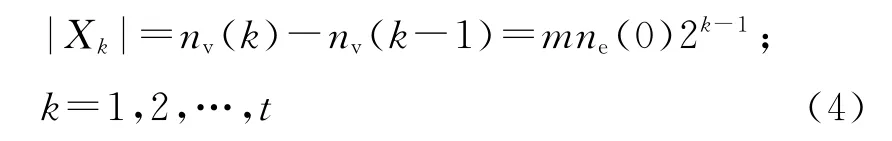
且有ne（0）2k条边界边，在SBEGN 模型N（t）中，最大度Δ（N（t））＝（tm＋1）·Δ（N（0）），最小度δ（N（t））＝2.则SBEGN 模型是一个稀疏网络，因为它的平均度〈k〉满足

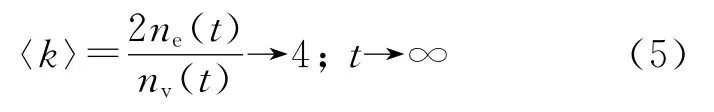
式（3）表明SBEGN 模型N（t）具有优先链接性，即新进入N（t）的节点与初始网络N（0）中的节点相连的概率较大.同时，N（t）的构造表明N（t）具有增长性，说明N（t）属于BA 无标度模型［3－4］.

以 下 用k（u，i）表 示 于 时 刻i节 点u在SBEGN 模型N（i）中所连接的边数目，用kt（u，i）表示节点u在N（i）中的具有最多叶子生成树中所连接的边数目.

为证明SBEGN 模型N（t）是层次网络，下面估算N（t）的每个节点的聚集系数.

（1）对初始网络N（0）的节点u∈V（0），设k（u，0）＝dj，那么，这个节点u在N（t）中的邻点的个数也就是它的度数，且k（u，t）＝（1＋tm）dj.记号Eu表示节点u的邻点之间的边集合，按照SBEGN 模型N（t）的构造，可计算出Eu的元素个数为｜Eu｜＝（1＋tm）dj.按照定义，节点u的聚集系数为

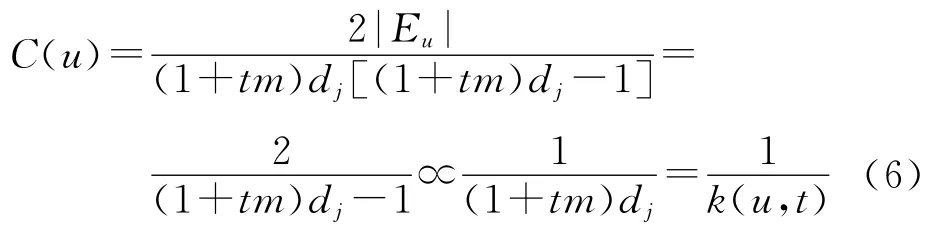
（2）对在i（＜t）时刻进入网络N（i）的节点v，且节点v又是N（i＋1）的一条边界边的端点，那么，在N（t）中，节点v的度数为k（v，t）＝2［（ti）m＋1］，它的邻点之间的边集合Ev有2（t－i）m＋1个元素.节点v的聚集系数为

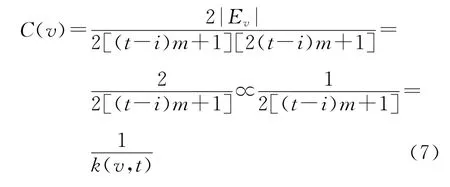
（3）对在j（＜t）时刻进入网络N（j）的节点w，且节点w又不是N（j＋1）的一条边界边的端点，则在N（t）中它的度数为k（w，t）＝2，它的邻点之间的边集合Ew仅有一个元素，所以

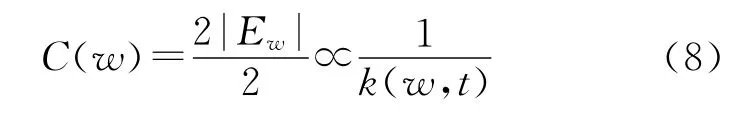
按照文献［11］和［12］的定律，上述式（6）～（8）关于节点聚集系数分布的式子证明SBEGN模型是层次网络，且对任何时刻t成立，即SBEGN 模型与好莱坞的演员网、WWW、代谢网络等属于同一类网络［12］，从而为本文的时间优先层次搜索算法提供了理论依据.图1给出SBEGN 模型的例子.

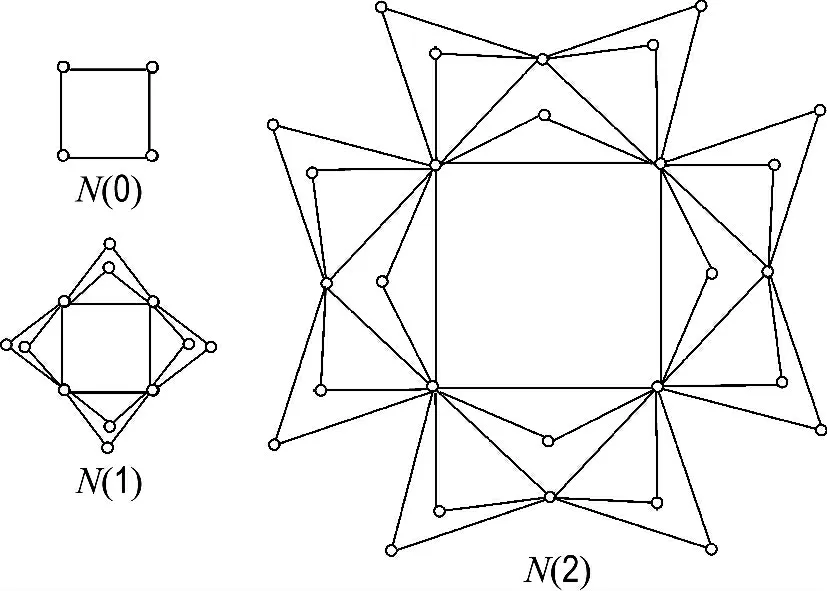
图1 当m＝2时，SBEGN 模型的N（0）、N（1）及N（2）Fig.1 N（0），N（1）and N（2）of SBEGN models when m＝2

2 SBEGN 模型的生成树

SBEGN 模型N（t）的生成树是一个连通且边数目最少的子网络，本章寻找N（t）的具有最多叶子的生成树.一般情形下，N（t）的具有最多叶子的生成树是不唯一的.用L（TM（t））表示N（t）的具有最多叶子的生成树TM（t）的全体叶子的集合.SBEGN 模型N（t）的生成树TM（t）具有如下的性质：

引理1 SBEGN 模型N（t）的任意一棵具有最多叶子的生成树TM（t）的叶子集合完全包含新进入N（t－1）的节点集合Xt.

证明 对任意时刻t≥1，假设存在节点w∈Xt，但wL（TM（t））.根据SBEGN 模型N（t）的构造，节点w的度数为k（w，t）＝2，且节点w与t－1时刻的SBEGN 模型N（t－1）的一条边界边uv的2个端点u和v分别相连.注意到，由于w不是TM（t）的叶子，则节点u和v至少有一个不是TM（t）的叶子，假设节点u不是叶子.则可以构造SBEGN 模型N（t）的另一棵生成树H如下：在TM（t）中删除边wv，连接边uv.显然w，v∈L（H），且生成树H的叶子数目｜L（H）｜≥｜L（TM（t））｜＋1，这违背TM（t）是N（t）的一棵具有最多叶子的生成树.本引理得证.□

引理2 设N（0）是给定的连通初始网络.对SBEGN 模型N（t），有

（Ⅰ）当t≥3 和L（TM（1））∩V（0）≠，则L（TM（t））∩V（0）＝.

（Ⅱ）当t≥2 和L（TM（1））∩V（0）＝，则L（TM（t））∩V（0）＝.

证明 为证结论（Ⅰ），假设存在叶子x∈L（TM（t））∩V（0），即L（TM（t））∩V（0）≠，设xy∈E（0），显然，yL（TM（t））.根据SBEGN 模型N（t）的构造和引理1，存在N（t）的一个2度节点wt，i∈Xt与节点x、wt－1，i∈Xt－1分别相连，则有wt－1，iL（TM（t）），并且wt，i∈L（TM（t））.注意到，节点wt－1，i的度数k（wt－1，i，t）≥3，也就是说，节点wt－1，i与节点x、wt，i、wt－2，i均相连.因为t－2≥3，如果wt－2，i∈L（TM（t）），导致wt，i、wt－1，i与其他节点不连接，这矛盾于TM（t）是树.下面构造N（t）的 另 一 棵 生 成 树H＊：删除边wt，iwt－1，i和wt－1，iwt－2，i；如果节点x在TM（t）中与节点y连接，将节点x与节点wt，i和wt－1，i分别相连；如果节点x在TM（t）中与节点u（≠y）连接，则删除边xu，然后将节点x与节点y连接.此时，｜L（H＊）｜≥｜L（TM（t））｜，矛盾于TM（t）是具有最多叶子生成树的事实.

结论（Ⅱ）的证明相同于结论（Ⅰ）的证明，故不赘述.□

定理1 当t≥3时，SBEGN 模型N（t）的每一棵具有最多叶子的生成树TM（t）的叶子数目为

且它的直径D（TM（t））不超过初始网络N（0）的具有最多叶子生成树TM（0）的直径D（TM（0））加上（2t－1）.

证明 为证明此定理，先给出时间优先层次搜索算法.

时间优先层次搜索算法（time－first levelsearching algorithm），简称为TFLS算法.

输入 一个SBEGN 模型N（t），t≥3.

输出N（t）的全体具有最多叶子的生成树TM（t），且每一棵TM（t）带有一个关于节点的时间序函数p.

步骤1 当k＝1，2时，FM（k）←｛N（k）的全体具有最多叶子的生成树｝.对每一棵具有最多叶子的生成树T0∈FM（k），定义V（T0）节点的一个时间序函数p为：若在V（T0）中，节点x的位置前于节点y的位置，则p（x）＜p（y），且有1＝min｛p（x）｜x∈V（T0）｝，｜V（T0）｜＝max｛p（x）｜x∈V（T0）｝.以下记号Nei（x）为与节点x有连线的节点集合.

步骤2s←1若t为奇数，否则s←2.

步骤3 如果s＜t－2，Gs←，到步骤4.如果s＝t－2，到步骤5.

步骤4 若FM（s）＼Gs＝，s←s＋1，到步骤3.否则，取Ts∈FM（s）＼Gs，V″←V（Ts），E″←E（Ts），T″←（V″，E″），Xs←，到步骤4.1.

步骤4.1 如果V（Ts）＼Xs＝，TM（s＋1）←T″；FM（s＋1）←FM（s＋1）∪｛TM（s＋1）｝，Gs←Gs∪｛Ts｝，到步骤4.如果V（Ts）＼Xs≠，到步骤4.2.

步骤4.2 取x∈V（Ts）＼Xs，使得p（x）＝min｛p（y）｜y∈V（Ts）＼Xs｝.若Nei（x）∩（V（s＋1）＼V″）＝，Xs←Xs∪｛x｝，到步骤4.1；否则，到步骤4.3.

步骤4.3Nei（x）∩（V（s＋1）＼V″）＝｛ux，1，ux，2，…，ux，m｝（m≥1），执行：p（ux，1）←p（u′）＋1，u′是V″的最后一个节点，然后把ux，1放进V″的最后 一 个 位 置 上；从j＝2 到m，p（ux，j）←p（ux，j－1）＋1，把ux，j放进V″的最后一个位置上.E″←E″∪｛xy｜y∈V″｝，T″←（V″，E″）；Xs←Xs∪｛x｝，到步骤4.1.

步骤5FM（t）←，F←.

步骤5.1 如果FM（t－2）＼F≠，取Tt－2∈FM（t－2）＼F，由上面的过程，知V（Tt－2）的节点有 一 个 时 间 序 函 数p；VH←V（Tt－2），EH←E（Tt－2），H←（VH，EH）；Xt←，到步骤5.2.如果FM（t－2）＼F＝，到步骤6.

步骤5.2 如果V（Tt－2）＼Xt≠，到步骤5.3；如果V（Tt－2）＼Xt＝，F←F∪｛Tt－2｝，到步骤5.1.

步骤5.3 取x∈V（Tt－2）＼Xt，使得p（x）＝min｛p（y）｜y∈V（Tt－2）＼Xt｝，若Nei（x）∩（V（t）＼V（t－2））＝，Xt←Xt∪｛x｝，到步骤5.2；否则，到步骤5.4.

步骤5.4Nei（x）∩（V（t）＼V（t－2））＝｛vx，1，vx，2，…，vx，n｝（n≥1）.执 行：p（vx，1）←p（u′）＋1，u′是VH的最后一个节点，然后把vx，1放进VH的最后一个位置上；从j＝2到n，p（vx，j）←p（ux，j－1）＋1，把ux，j放进VH的最后一个位置上.EH←EH∪｛xy｜y∈VH｝，H←（VH，EH）.Xt←Xt∪｛x｝.FM（t）←FM（t）∪｛H｝，到步骤5.2.

步骤6 返回FM（t），且FM（t）的每一棵具有最多叶子的生成树TM（t）带有一个时间序函数p.

根据引理2，TFLS算法的步骤3中s＝t－2成立.因为SBEGN 模型N（k）中的Xk里有个节点成为N（k）的边界边的端点，则在SBEGN 模型N（k＋1）中，这些节点与新增加的节点连线，且当k≥2，它们不可能是TM（k＋1）的叶子.根据TFLS算法，有如下的递归公式：

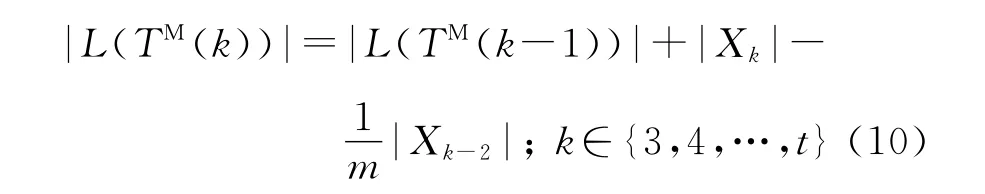
根据｜L（TM（2））｜＝｜X2｜＋｜X1｜，整理得

联立式（4），可求得｜L（TM（t））｜的精确值为

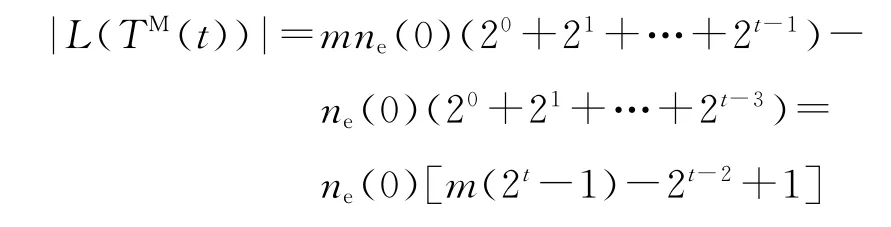
根据TFLS算法找到TM（t）的过程，是每次给TM（t－1）添加叶子得到生成树TM（t），即给TM（t－1）的最长路径增加了2.则当t≥3 时，D（TM（t））不超过初始网络N（0）的具有最多叶子生成树TM（0）的直径加上（2t－1）.□

图2给出用算法找到图1中SBEGN 模型的3个具有最多叶子的生成树.

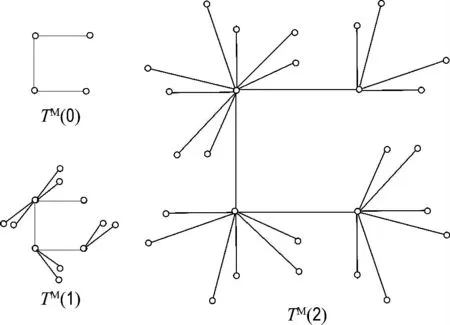
图2 当m ＝2 时，3棵生成树TM （0）、TM（1）和TM（2）Fig.2 Three spanning trees TM（0），TM（1）and TM（2）when m ＝2

3 TFLS算法找到的生成树的性质

由定理1可得出下面2个极限.

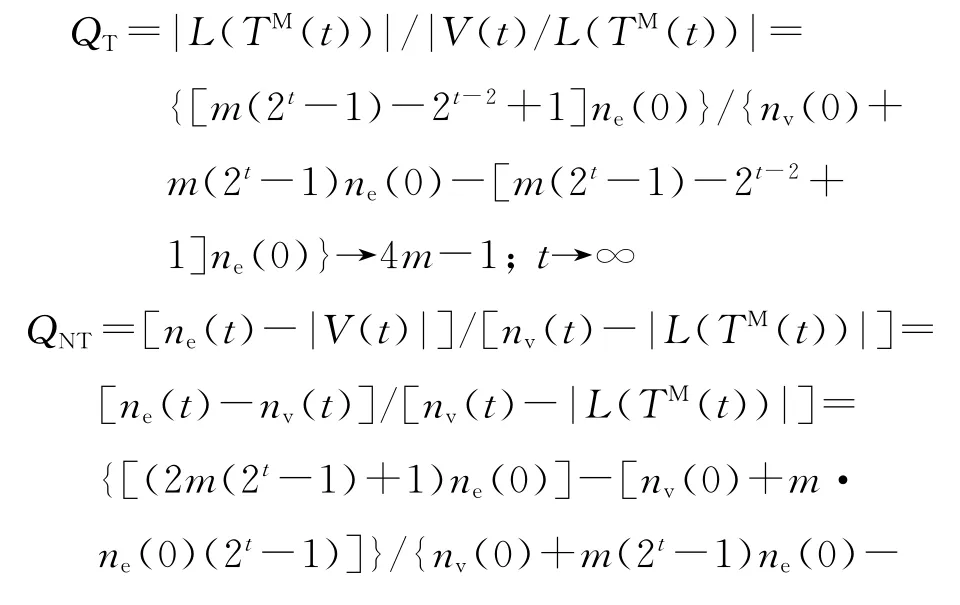
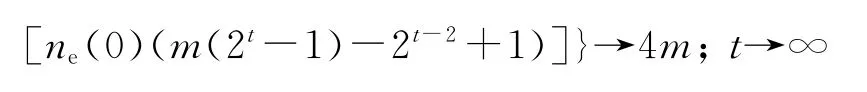
上述两个极限说明，当时间t足够大时，比值QT几乎等价于比值QNT，即QT～QNT.因此可以尝试用生成树TM（t）来解释SBEGN 模型N（t）的一些性质.

下面讨论生成树TM（t）的度谱.前面提到初始网络N（0）节点不同的度数为d1，d2，…，da，且d1＞d2＞…＞da.TFLS算法找到的生成树TM（t）的节点数目与度数的度谱在表1中给出，其中t时刻度数为d的节点个数为nd（t），f（di）＝tm（di

表1 TFLS算法找到的生成树TM（t）的度谱Tab.1 The spectrum of spanning tree TM（t）by applying the TFLS algorithm

由于生成树TM（t）的度谱是离散型，可以计算它的随机选择恰好有k边的节点的概率P（k）.根据文献［3］使用的统计技术和式（4），可得下面的式子：

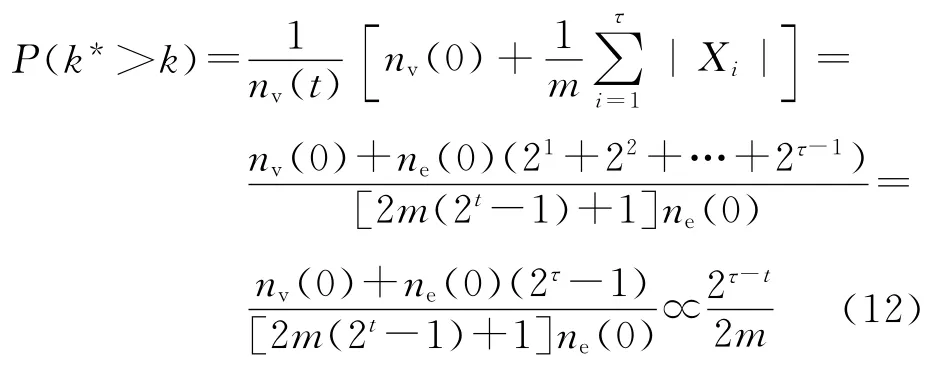
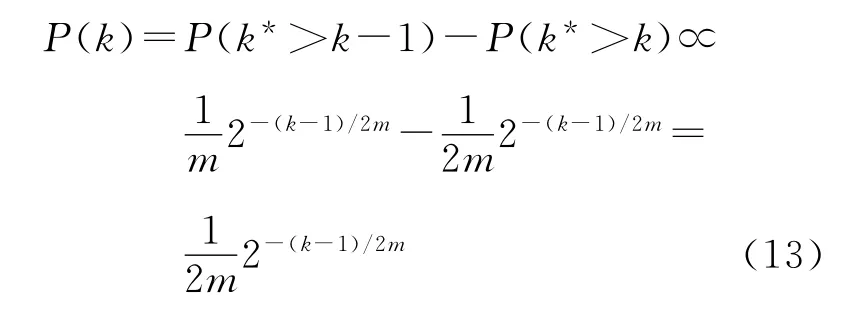
上式说明，最多叶子的生成树TM（t）服从指数分布，TM（t）亦为指数型生成树.

在j（＜t）时刻，最多叶子的生成树TM（j）的顶点数目为｜V（TM（j））｜＝nv（j），则它的累积分布为

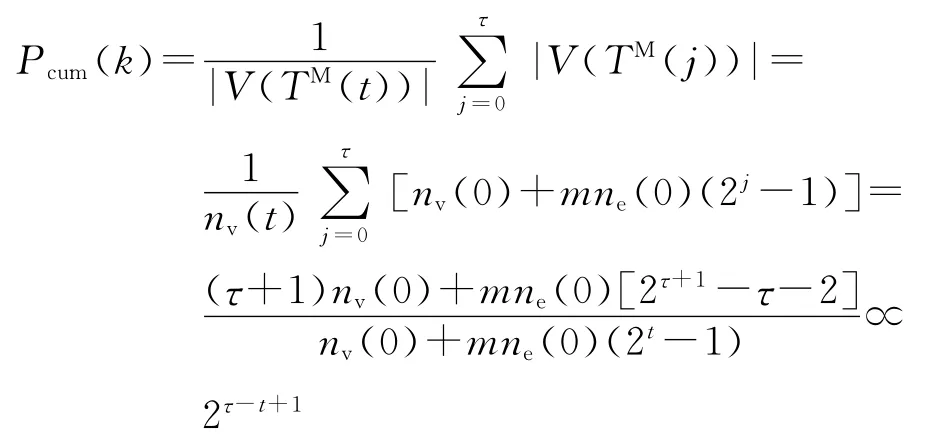
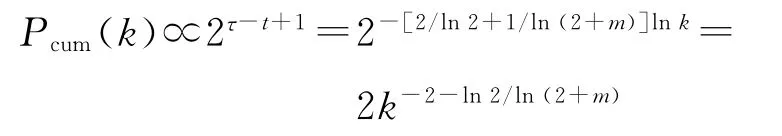
下面再给出关于SBEGN 模型的具有最多叶子的生成树的结论.

定理2 当t≥3时，SBEGN 模型N（t）的任意2棵具有最多叶子的生成树TMi（t）和TMj（t）拥有相同的叶子集合，即L（TMi（t））＝L（TMj（t））.

证明 令Li＝L（TMi（t））和Lj＝L（TMj（t））.注意到t≥3，由引理2，Li∩V（0）＝＝Lj∩V（0）.设有u∈Li，但uLj.由于Li∩N（0）＝，不妨设u是给N（k）的边界边xy添加的m个节点中的一个.它在Lj中的度数kt，j（u，t）满足2［（t－k）m＋1］≥kt，j（u，t）≥2，它在N（t）中的度数k（u，t）＝2或k（u，t）＝2［（t－k）m＋1］.

情形1 如果u不是N（k＋1）的任何边界边的端点，则它在N（t）中的度数k（u，t）＝2，故kt，j（u，t）＝1.构造N（t）的另一棵生成树H＝Lj－uy＋xy，即在Lj中删去边uy，然后将x和y连接.显然，｜L（H）｜＞｜L（TMj（t））｜，矛盾.这是由于u是H的叶子，而Lj的其他节点的属性在H中没有发生变化.

情形2 如果u是N（k＋1）的边界边的端点，那么，度数kt，j（u，t）≥3，且它在N（t）中的度数为k（u，N（t））＝2［（t－k）m＋1］.根据上面节点u∈Li的属性，在N（t）中，节点x和u与节点x1，x2，…，xm均相连，节点y和u与节点y1，y2，…，ym均相连.根据引理1和u∈Li，得xr，yr∈Li，r＝1，2，…，m.因为t≥3，则在N（t）中，有度数k（x，t）≥2和k（y，t）≥2.根据引理2，xLi和yLj.对TMj（t）实施如下运算：删去边uy将x与y连接，然后对r＝1，2，…，m，将xr与x连接，将yr与y连接，得到新的生成树H′.由于u∈L（H′），而且TMj（t）的其余节点的属性在H′中没有发生变化，也就是说｜L（H′）｜＞｜L（TMj（t））｜，这与TMj（t）是最多叶子生成树的假定矛盾.

综合上述2种情形的推证，L（TMi（t））＝L（TMj（t））.□

由于SBEGN 模型是层次网络，运用以上结论不难证明：当t≥3时，SBEGN 模型N（t）的一棵具有最多叶子生成树TM（t）包含次一级SBEGN 模型N（t－1）的一棵具有最多叶子的生成树TM（t－1）.

4 结 语

本文构造了SBEGN 模型N（t），并设计了时间优先层次搜索算法，随后找出SBEGN 模型N（t）的具有最多叶子的生成树TM（t），确定了任何具有最多叶子的生成树的拓扑性质.需要指出的是，本文的SBEGN 模型具有良好的性质：当t≥3时，N（t）的任意2棵具有最多叶子的生成树TMi（t）和TMj（t）拥有相同的叶子集合，且N（t）为层次网络，它的直径小于生成树TM（t）的直径，换句话说，N（t）是小世界网络模型.这些良好的性质不仅为实际网络建设提供了可靠的理论依据，更重要的是为模拟实际网络提供了易于理解和掌握的工具，并不断产生优化型算法.作为进一步研究的方向，将考虑模型的随机增加连线或者随机删除连线，这样的研究对实际网络的模拟会更有价值.显然，确定这种网络模型的拓扑性质以及找到它们的具有最多叶子的生成树将是研究的关键，也是研究的难点.

［3］ ZHANG Zhong－zhi，RONG Li－li，GUO Chong－hui.A deterministic small－world network created by edge iterations［J］.Physica A：Statistical Mechanics and its Applications，2006，363（2）：567－572.

［4］ Pastor－Satorras R，Vespignani A.Epidemic spreading in scale－free networks ［J］.Physical Review Letters，2001，86（14）：3200－3203.

［5］ ZHENG Geng－zhong，LIU San－yang，QI Xiaogang.Scale－free topology evolution for wireless sensor networks with reconstruction mechanism［J］.Computers and Electrical Engineering，2012，38（3）：643－651.

［6］ Perlman R.Hierarchical networks and the subnetwork partition problem ［J］.Computer Networks and ISDN Systems，1985，9（4）：297－303.

［7］ Kleinberg J.The small－world phenomenon：An algorithmic perspective［C］／／Proceedings of the 32nd Annual ACM Symposium on Theory of Computing，STOC 2000.New York：Association for Computing Machinery，2000：163－170.

［8］ Adamic L A，Adar E.How to search a social network［J］.Social Networks，2005，27（3）：187－203.

［9］ Kim Dong－hee，Noh Jae－dong，Jeong Ha－woong.Scale－free trees：The skeletons of complex networks［J］.Physical Review E—Statistical Nonlinear，and Soft Matter Physics，2004，70（42）：046126.

［10］ Bondy J A，Murty U S R.Graph Theory with Applications ［M］.Amsterdam：North Holland，1976.

［11］ Dorogovtsev S N，Goltsev A V，Mendes J F F.Pseudofractal scale－free web ［J］.Physical Review E—Statistical Nonlinear，and Soft Matter Physics，2002，65（6）：066122.