一种求解正交约束问题的投影梯度方法
2015-03-15丁卫平
童 谣, 丁卫平
(1. 福州大学 数学与计算机科学学院, 福州 350108; 2. 湖南理工学院 数学学院, 湖南 岳阳 414006)
一种求解正交约束问题的投影梯度方法
童 谣1, 丁卫平2
(1. 福州大学 数学与计算机科学学院, 福州 350108; 2. 湖南理工学院 数学学院, 湖南 岳阳 414006)
正交约束优化问题在特征值问题、稀疏主成分分析等方面有广泛的应用. 由于正交约束的非凸性, 精确求解该类问题具有一定的困难. 本文提出了一种求解正交约束优化问题的投影梯度算法. 该算法采用施密特标准正交化方法处理正交约束, 其时间复杂度为O(r2n), 比传统SVD分解复杂度低, 且实现简单. 数值实验验证了算法的有效性.
正交约束优化; 投影梯度算法; 邻近点算法; 施密特标准正交化
引言
正交约束优化模型在科学与工程计算相关领域有广泛应用, 譬如: 线性和非线性特征值问题[1,2], 组合优化问题[3,4], 稀疏主成分分析问题[5,6], 人脸识别[7], 基因表达数据分析[8], 保角几何[10,11], 1-比特压缩传感[12~14], p-调和流[15~18], 等等, 都离不开正交约束优化模型.
一般地, 正交约束优化问题有如下形式:

其中F(X)是ℝn×r→ℝ的可微函数,Q是对称正定阵,I是r×r单位阵,n≥r. 由于Q是对称正定的, 可设Q=LT L. 令Y=LX, 则(1)可转化为:
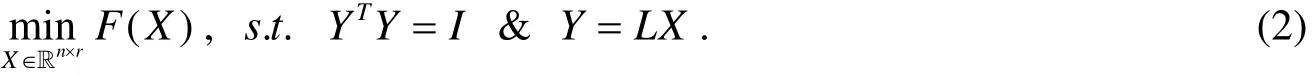
线性约束优化问题的求解技术已经比较成熟, 为了简化问题(2)的形式, 我们主要考虑求解如下正交约束优化问题:

由于正交约束的非凸性, 精确求解问题(1)或(3)具有一定的挑战. 目前为止, 还没有有效的算法可以保证获取这类问题的全局最优解(除了某些特殊情况, 如: 寻找极端特征值). 由于保持正交约束可行性的计算代价太大, 为了避免直接处理非线性约束, 人们提出了很多方法, 将带约束的优化问题转化成无约束的优化问题求解. 这些方法中, 最常用的有罚函数方法[21,22]和增广拉格朗日方法[19,20].
罚函数方法将正交约束违背作为惩罚项添加到目标函数中, 把约束优化问题(3)转化为如下无约束优化问题:

其中ρ>0为罚参数. 当罚参数趋于无穷大时, 罚问题(4)与原问题(3)等价. 为了克服这个缺陷, 人们引入了标准增广拉格朗日方法. Wen和Yang等[23]提出用Lagrange方法求解问题

并证明了算法收敛于问题的可行解(在正则条件下, 收敛到平衡点). 最近, Manton[24,25]等提出了解决正交约束问题的Stiefel manifold 结构方法: Osher[26]等提出一种基于Bregman迭代的SOC算法. SOC算法结合算子分裂与Bregman迭代方法, 将正交约束问题转化为交替求解一个无约束优化问题和一个具有解析解的二次约束优化问题, 该方法获得了不错的数值实验效果. SOC算法在处理矩阵正交约束的子问题时,使用了传统的SVD分解, 其时间复杂度为O(n3).
在本文中, 我们提出一种新的处理正交约束的算法, 该算法计算复杂性比传统的SVD分解要低. 根据问题(3)约束条件的特殊性, 我们将问题求解过程分解为两步: 第一步, 采用邻近点算法求解松弛的无约束优化问题, 得到预测点; 第二步, 将预测点投影到正交约束闭子集上. 基本的数值结果说明了这种正交闭子集投影梯度算法优越于经典增广Lagrange算法.
1 算法描述
本节给出求解正交约束优化问题的正交闭子集上的投影梯度算法(简记为POPGM). 该方法分为两步: 首先, 采用邻近点算法求解松弛的无约束优化问题, 得到预测点; 然后, 将预测点投影到正交闭子集上, 其中投影算子是一个简单的斯密特标准正交化过程. 为此, 我们先简要介绍邻近点算法.
1.1 经典邻近点算法
求解无约束优化问题的方法有很多, 包括: 最速下降法, Barzilai-Borwein method[30], 外梯度方法[31],等等. 这里, 我们介绍一种有效的求解算法, 邻近点算法(Proximal Point Algorithm, 简记为PPA)[27,28]. 最初, Rockafellar等[32]提出了求解变分不等式问题的PPA算法. 对于抽象约束优化问题:

1.2 投影梯度算法
现在给出本文提出的邻近点正交约束投影梯度算法(POPGM):
Step 0. 给定初始参数r0>0,v=0.95, 初始点X0∈Ω, 给定ε>0,ρ>1, 令k=0.

注: 子问题(10)等价于求解如下单调变分不等式

变分不等式(12)可采用下述显示投影来获得逼近解:

由于(11)和(13)均有显示表达式, 可知和Xk都是易于求解的. 另外, 由于r< 本节通过实例来说明POPGM算法的有效性. 实验测试环境为Win7系统, Intel(R)Core i3, CPU .20GHz, RAM 2.0GB, 编程软件为MATLAB R2012b. 测试问题及数据取自Yin0. 给定对称矩阵A∈ℝn×n, 和酉矩阵V∈ℝn×r, 当V是前r个最大特征值所对应特征空间的一组正交基时, 函数Trace(VT AV)达到最大值. 该问题可以考虑为求解如下正交约束优化问题: 其中λ1≥λ2≥…≥λr是我们要提取A的r个最大的特征值,A∈ℝn×n为对称正定矩阵. 初始点:X0=randn(n,r),X0=orth(X0). 下面采用三种算法求解上述问题, 分别是本文的POPGM算法, Yin0的algorithm 2(简记为Yin’s Algo.)与MATLAB工具包中的“eigs”函数. 表中的FP/FY/FE分别表示通过运行POPGM、Yin’s Algo和Eigs所求得的r个最大特征值之和, 即目标函数值; win表示两种算法对比, 所获得的目标函数值之差; err表示可行性误差, 即: e. 表1给出了对于固定r=6,n在500到5000之间变化时, 三种算法在求解问题的迭代次数(iter)与CPU时间(cput)的对比结果. 由表1可知, POPGM迭代次数受矩阵维数影响不大. 随着矩阵维数的增大, POPGM算法与Yin’s Algo.相比, 当n≤2000时, POPGM不仅时间上有优势, 而且提取效果也较好(win>0);n≥3000时, POPGM时间花费略多, 但提取效果有明显优势. POPGM与“eigs”相比, 随着维数n的增大, 时间优势逐渐变大, 但提取变量的解释能力也逐渐减弱. 由实验结果可知, 当矩阵维数n较大时, POPGM有较好的表现. 表2列出了固定n=3000, 提取特征值的个数r在1到23之间变化时POPGM的运行结果. 由表2可以看出, 当r越小, POPGM计算花费时间越少; 随着r增大,FP增大, 时间花费也在增大; 当r取5到7时, 花费时间合适, 且提取效果较好. 表1 固定r = 6时变化矩阵维数的结果对比(CPU以秒为单位) 表2 固定n = 2000, r变化时POPGM的求解结果 表3列出了固定提取r=6, 将POPGM算法框架中的正交化过程替换成SVD分解, 对比两种处理正交约束方法的求解结果. 由表3可知, 在POPGM算法框架下, 在正交约束闭子集上的投影算子比传统的SVD分解在运算时间上要节约很多; 同时, 两种方法所提取的特征之和保持一致, 不随维数变化而变化,时间优势随矩阵维数增大而增大. 可见, 本文提出的处理正交约束的方法非常有效. 表3 固定r = 6, POPGM框架下的投影算子与SVD分解的结果对比 本文研究求解一类正交约束优化问题的快速算法. 结合邻近点算法和施密特标准正交化过程, 本文提出了基于邻近点算法的非精确投影梯度算法, 算法采用邻近点算法求解松弛的无约束优化问题, 得到预测点; 然后, 将预测点投影到正交约束闭子集上. 与传统的增广拉格朗日法、罚函数方法的主要区别在于POPGM在每一步迭代中通过在正交约束集上投影得到迭代解, 并且避免使用SVD分解, 加快了算法的运行速度. 数值实验说明本文提出的POPGM有较好的综合表现. [1] Edelman A., As T., Arias A., Smith T., et al.The geometry of algorithms with orthogonality constraints[J]. SIAM J. Matrix Anal. Appl., 1998, 20 (2): 303~353 [2] Caboussat A., Glowinski R., Pons V.An augmented lagrangian approach to the numerical solution of a non-smooth eigenvalue problem[J]. J. Numer. Math., 2009, 17 (1): 3~26 [3] Burkard R. E., Karisch S. E., Rendl F.Qaplib-a quadratic assignment problem library[J]. J. Glob. Optim., 1997, 10 (4): 291~403 [4] Loiola E. M., de Arbreu N. M. M., Boaventura –Netto P. O., et al.A survey for the quadratic assignment problem[J]. Eur. J. Oper. Res., 2007, 176 (2): 657~690 [5] Lu Z. S., Zhang Y.An augmented lagrangian approach for sparse principal component analysis[J]. Math. Program., Ser. A., 2012, 135: 149~193 [6] Shen H., Huang J. Z.Sparse principal component analysis via regularized low rank matrix approximation[J]. J. Multivar. Anal., 2008, 99 (6): 1015~1034 [7] Hancock P. Burton A., Bruce V.Face processing: human perception and principal components analysis[J]. Memory Cogn., 1996, 24: 26~40 [8] Botstein D.Gene shavingas a method for identifying distinct sets of genes with similar expression patterns[J]. Genme Bil., 2000, 1: 1~21 [9] Wen Z., Yin W. T.A feasible method for optimization with orthogonality constraints[J]. Math. Program., 2013, 143(1-2): 397~434 [10] Gu X., Yau S.Computing conformal structures of surfaces[J]. Commun. Inf. Syst., 2002, 2 (2): 121~146 [11] Gu X., Yau S. T.Global conformal surface parameterization[C]. In Symposium on Geometry Processing, 2003: 127~137 [12] Boufounos P. T., Baraniuk R. G. 1-bit compressive sensing[C]. In Conference on information Sciences and Systems (CISS), IEEE, 2008: 16~21 [13] Yan M., Yang Y., Osher S.Robust 1-bit compressive sensing using adaptive outlier pursuit[J]. IEEE Trans, Signal Process, 2012, 60 (7): 3868~3875 [14] Laska J. N., Wen Z., Yin W., Baraniuk R. G.Trust, but verify: fast and accurate signal recovery from 1-bit compressive measurements[J]. IEEE Trans. Signal Process, 2011, 59 (11): 5289 [15] Chan T. F., Shen J.Variational restoration of nonflat image features: models and algorithms[J]. SIAM J. Appl. Math., 2000, 61: 1338~1361 [16] Tang B., Sapiro G., Caselles V.Diffusion of general data on non-flat manifolds via harmonic maps theory: the direction diffusion case[J]. Int. J. Comput. Vis., 2000, 36: 149~161 [17] Vese L. A., Osher S.Numerical method for p-harmonic flows and applications to image processing[J]. SIAM J. Numer. Anal., 2002, 40 (6): 2085~2104 [18] Goldfarb D., Wen Z., Yin W.A curvilinear search method for the p-harmonic flow on spheres[J]. SIAM J. Imaging Sci., 2009, 2: 84~109 [19] Glowinski R., Le Tallec P.Augmented Lagrangian and operator splitting methods in nonlinear mechanics[J]. SIAM Studies in Applied Mathematics, Society for Industrial and Applied Mathematics(SIAM), Philadelphia, PA, 1989, 9 [20] Fortin M., Glowinski R.Augmented Lagrangian methods: applications to the numerical solution of boundary-value problems[J]. North Holland, 2000, 15 [21] Nocedal J., Wright S. J.Numerical Optimization[M]. Springer, New York, 2006 [22] Brthuel F., Brezis H., Helein F.Asymptotics for the minimization of a ginzburg-landau functional[J]. Calc. Var. Partial. Differ. Equ., 1993, 1 (2): 123~148 [23] Wen Z., Yang C., Liu X.Trace-penalty minimization for large-scale eigenspace computation[J]. J. Scientific Comput., to appear [24] Manton J. H.Optimization algorithms exploiting unitary constraints[J]. IEEE Trans. Signal Process, 2002, 50 (3): 635~650 [25] Absil P. -A., Mahony R., Sepulchre R.Optimization algorithms on matrix manifolds[M]. Princeton University Press, Princeton, 2008 [26] Lai R., Osher S.A splitting method for orthogonality constrained problem[J]. J Sci Comput., 2014, 58 (2): 431~449 [27] He B. S., Fu X. L. and Jiang Z. K.Proximal point algorithm using a linear proximal term[J]. J. Optim. Theory Appl., 2009, 141: 209~239 [28] He B. S., Yuan X. M.Convergence analysis of primal-dual algorithms for a saddle-point problem: From contraction perspective[J]. SIAM J. Imaging Sci., 2012, 5: 1119~149 [29] Barzilai J., Borwein J. M.Two-point step size gradient methods[J]. IMA J. Numer. Anal., 1988, 8: 141~148 [30] Korpelevich G. M.The extragradient method for finding saddle points and other problems[J]. Ekonomika Matematicheskie Metody, 1976, 12: 747~756 [31] Rockafellar R. T.Monotone operators and the proximal point algorithms[J]. SIAM J. Cont. Optim., 1976, 14: 877~898 A Projection Gradient Method for Orthogonality Constrained Optimization Problems TONG Yao1, DING Wei-ping2 The orthogonality constrained problems has wide applications in eigenvalue problems, sparse principal component analysis, etc. However, it is challenging to solve orthogonality constrained problems due to the non-convexity of the equality constraint. This paper proposes a projection gradient method using Gram-Schmidt process to deal with the orthogonality constraint. The time complexity is bounded byO(r2n), which is lower than the classical SVD. Some primary numerical results verified the validity of the proposed method. orthogonal constrained optimization; projection gradient method; proximal point algorithm; gram-schmidt process O224 A 1672-5298(2015)02-0005-05 2015-04-06 童 谣(1991− ), 女, 安徽铜陵人, 福州大学数学与计算机科学学院硕士研究生. 主要研究方向: 优化理论、算法及其应用2 数值实验


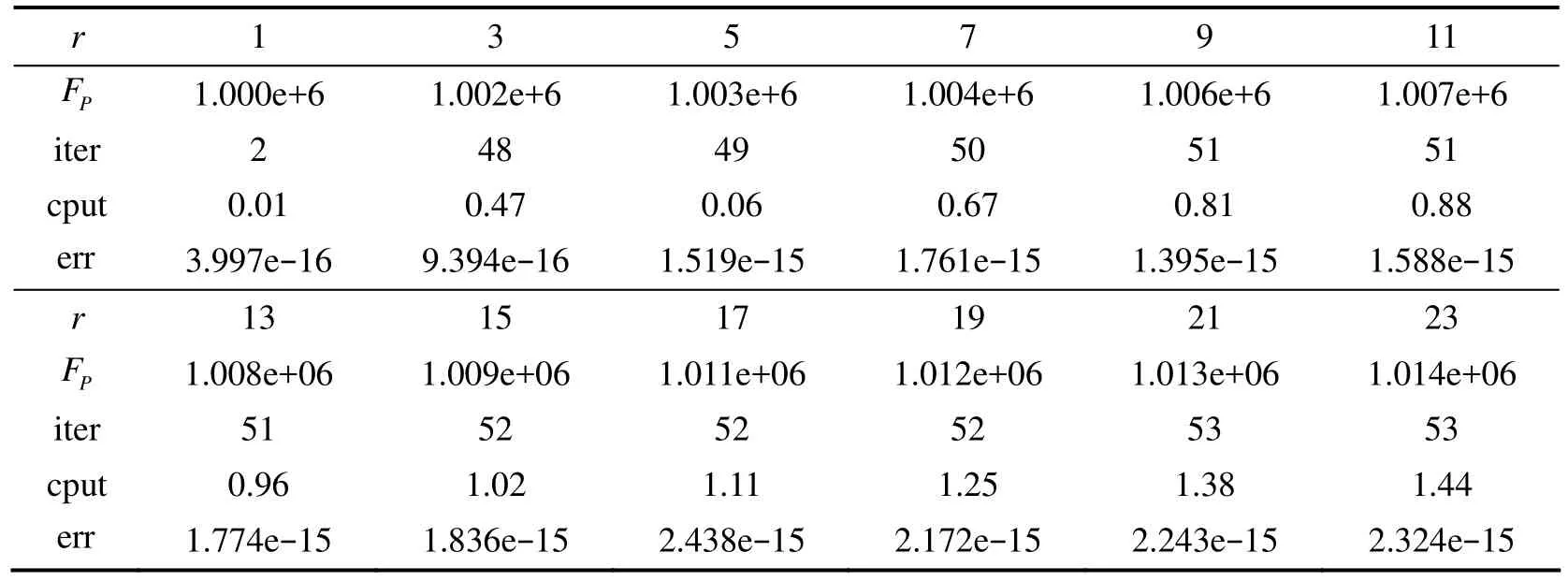
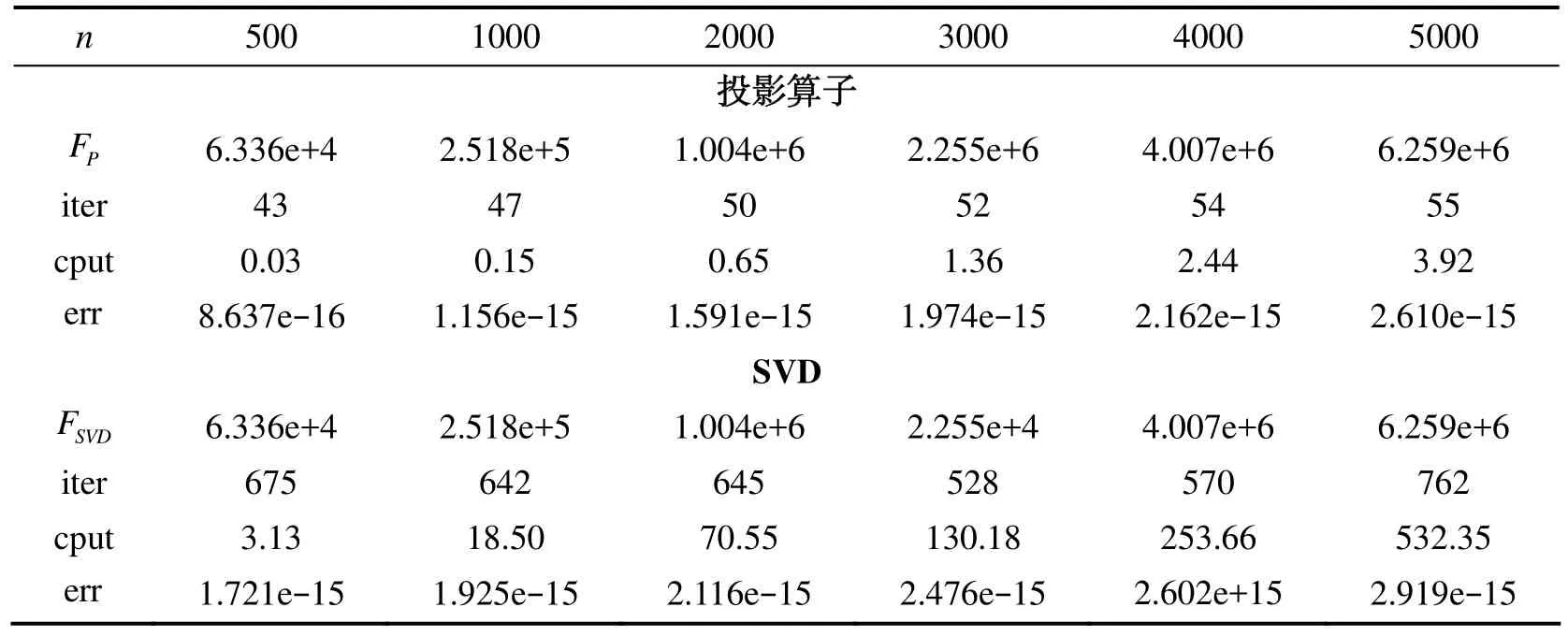
3 结论
(1. College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350108, China; 2. College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)
