Wang Shengxiang　 Wang Shuanhong

(1Department of Mathematics, Southeast University, Nanjing 211189, China)(2School of Mathematics and Statistics, Chuzhou University, Chuzhou 239000, China)



Enveloping algebras of generalizedH-Hom-Lie algebras

Wang Shengxiang1,2Wang Shuanhong1

(1Department of Mathematics, Southeast University, Nanjing 211189, China)(2School of Mathematics and Statistics, Chuzhou University, Chuzhou 239000, China)

Abstract：Let H be a Hopf algebra and YD the Yetter-Drinfeld category over H. First, the enveloping algebra of generalized H-Hom-Lie algebra L, i.e., Hom-Lie algebra L in the category YD, is constructed. Secondly, it is obtained that U(L)=T(L)/I, where I is the Hom-ideal of T(L) generated by {l⊗l′-l(-1)·l′⊗l,l′∈L}, and u:L→T(L)/I is the canonical map. Finally, as the applications of the result, the enveloping algebras of generalized H-Lie algebras, i.e., the Lie algebras in the category YD and the Hom-Lie algebras in the category of left H-comodules are presented, respectively.

Key words：enveloping algebra; generalized H-Hom-Lie algebra; Yetter-Drinfeld category

Received 2013-10-07.

Biographies：Wang Shengxiang (1979—), male, doctor, wangsx-math@163.com; Wang Shuanhong (corresponding author), male, doctor, professor, shuanhwang@seu.edu.cn.

Foundation items：The National Natural Science Foundation of China (No.11371088), the Excellent Young Talents Fund of Anhui Province (No.2013SQRL092ZD), the Natural Science Foundation of Higher Education Institutions of Anhui Province (No.KJ2015A294), China Postdoctoral Science Foundation (No.2015M571725), the Excellent Young Talents Fund of Chuzhou University (No.2013RC001).

Citation：Wang Shengxiang, Wang Shuanhong. Enveloping algebras of generalizedH-Hom-Lie algebras[J]．Journal of Southeast University (English Edition),2015,31(4):588-590．[doi:10.3969/j.issn.1003-7985.2015.04.027]

Hom-Lie algebras were first studied by Hartwig et al. in Ref.[1], where they introduced the structure of the Hom-Lie algebras in the context of the deformations of Witt and Virasoro algebras. The ideal is that the Jacobi identity is replaced by the so-called Hom-Jacobi identity, namely,

[α(x),[y,z]]+[α(y),[z,x]]+[α(z),[x,y]]=0

whereαis an endomorphism of Lie algebras. Hom-algebras were first studied by Makhlouf and Silvestrov in Ref.[2], in which the associativity is replaced by the Hom-associativity, namely,

α(x)(yz)=(xy)α(z)

Dually, Makhlouf et al.[3-4]gave the Hom-coassociativity for Hom-coalgebras. Later, Chen et al.[5]studied Hom-Lie bialgebras as a natural generalization of Lie bialgerbas. Caenepeel and Goyvaerts[6]studied Hom-Hopf algebras from a categorical view point, and Yau[7]introduced the notion of quasitriangular Hom-Hopf algebras. Also, he proved that each quasitriangular Hom-Hopf algebra produces a solution of the Hom-Yang-Baxter equation, and constructed the enveloping algebras of Hom-Lie algebras in Ref.[8].

Motivated by Wang et al.[9], we considered Hom-Lie algebras in Yetter-Drinfeld categories and proved that eachH-Hom-algebra gives rise to a generalizedH-Hom-Lie algebra. It is a natural question whether we can construct enveloping algebras of generalizedH-Hom-Lie algebras or not. This paper will give a positive answer to this question.

Throughout this paper, all algebraic systems are supposed to be over a fieldk. About the Hom-algebras and Hom-Lie algebras, the readers can be referred to Caenepeel and Goyvaerts[6]as general references, about Hopf algebras to Sweedler[10]and Yetter-Drinfeld categories to Radford[11]. IfCis a coalgebra, we use the Sweedler-type notation for the comultiplication:Δ(c)=c1⊗c2, for allc∈C.

1GeneralizedH-Hom-Lie Coalgebras

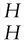
ρ(h·m)=h1m(-1)S(h3)⊗h2·m0

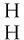
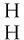
(a(-1)·b)(-1)·a0⊗(a(-1)·b)0=a⊗ba,b∈A

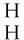
α(a)(bc)=(ab)α(c), α(ab)=α(a)α(b)

a1A=1Aa=α(a), α(1A)=1Aa,b,c∈A

1) H-anti-commutativity

[l, l′]=-[l(-1)·l′, l0]l, l′∈L

2) H-Hom-Jacobiidentity

{l⊗l′⊗l"}+(τ⊗1)(1⊗τ){l⊗l′⊗l"}+

(1⊗τ)(τ⊗1){l⊗l′⊗l"}=0

foralll, l′, l"∈L,where{l⊗l′⊗l"}denotes[α(l), [l′, l"]].

Proposition1[9]Let(A, α)beanH-Hom-algebra.AssumethatthebraidingτissymmetriconA.Thenthetriple(A, [,], α)isageneralizedH-Hom-Liealgebra,wherethebracketproductisdefinedby

[,]:A⊗A→A, [a, b]=ab-(a(-1)·b)a0a, b∈A

α-1(c1)⊗Δ(c2)=Δ(c1)⊗α-1(c2)

Δ(α(c))=α(c1)⊗α(c2)

c1ε(c2)=α-1(c)=ε(c1)c2, ε(α(c))=ε(c)

1) H-anti-cocommutativity

δ=-τδ

2) H-Hom-coJacobiidentity

(1+(τ⊗1)(1⊗τ)+(1⊗τ)(τ⊗1))(α⊗δ)δ=0

Proposition2Let(C, Δ, α)beageneralizedH-Hom-coalgebra.AssumethatthebraidingτissymmetriconC.Thenthetriple(C, δ, α)isageneralizedH-Hom-Liecoalgebra,wherethecobracketisdefinedby

δ:C→C⊗C, δ(c)=c1⊗c2-(c1(-1)·c2)⊗c10c∈C

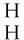
δ(h·c)=(h·c)1⊗(h·c)2-((h·c)1(-1)·(h·c)2)⊗

(h·c)10=h1·c1⊗h2·c2-(h11c1(-1)S(h13))·

(h2·c2)⊗h12·c10=h1·c1⊗h2·c2-

h1c1(-1)·c2⊗h2·c10=h·(c1⊗c2)-

h·(c1(-1)·c2⊗c10)

Soδis leftH-linear. We can also conclude that

(1⊗δ)ρ(c)=c(-1)⊗(c01⊗c02-c01(-1)·c02⊗c010)=

c1(-1)c2(-1)⊗(c10⊗c20-c10(-1)·c20⊗c100)

ρδ(c)=c1(-1)c2(-1)⊗c10⊗c20-(c1(-1)·c2)(-1)c10(-1)⊗

(c1(-1)·c2)0⊗c100=c1(-1)c2(-1)⊗c10⊗c20-c1(-1)1c2(-1)S(c1(-1)3)c10(-1)⊗c1(-1)2·c20⊗c100=

c1(-1)c2(-1)⊗(c10⊗c20-c10(-1)·c20⊗c100)

Hence, (1⊗δ)ρ=ρδ, that is,δis leftH-colinear.

Next, we verify that the cobracketδis compatible withα. In fact, for anyc∈C, we obtain

δα(c)=α(c)1⊗α(c)2-(α(c)1(-1)·α(c)2)⊗α(c)10=

α(c1)⊗α(c2)-(α(c1)(-1)·α(c2))⊗α(c1)0=

α(c1)⊗α(c2)-c1(-1)·α(c2)⊗α(c10)=

α(c1)⊗α(c2)-α(c1(-1)·c2)⊗α(c10)

as required. To show that (C,Δ,α) is a generalizedH-Hom-Lie coalgebra in the sense of Definition 4, we verify theH-anti-cocommutativity andH-Hom-coJacobi identity. However, this is a routine work sinceτis symmetric onC. This completes the proof.

2Enveloping Algebras of GeneralizedH-Hom-Lie Algebras

In this section, we will construct the enveloping algebraU(L) of a generalizedH-Hom-Lie algebraL.

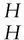
fα1=α2f,f([x,y]L1)=[f(x),f(y)]L2

for allx,y∈L1.

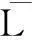
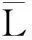
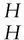
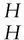
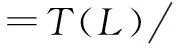
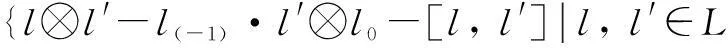
h·(l⊗l′-l(-1)·l′⊗l0-[l,l′])=

h1·l⊗h2·l′-h1l(-1)·l′⊗h2·l0-[h1·l,h2·l′]=h1·l⊗h2·l′-(h1·l)(-1)·(h2·l′)⊗(h1·l)0-[h1·l,h2·l′]=h1·l⊗h2·l′-h1l(-1)S(h3)·

(h4·l′)⊗h2·l0-[h1·l,h2·l′]=h1·l⊗

h2·l′-h1·(l(-1)·l′)⊗h2·l0-[h1·l,h2·l′]∈I

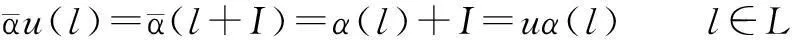
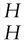
f([l,l′])=[f(l),f(l′)]=

f(l)f(l′)-(f(l)(-1)·f(l′))f(l)0

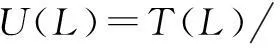
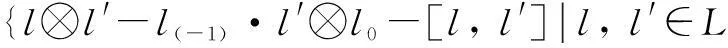
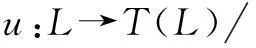
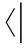
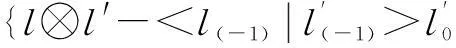
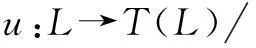
References

[1]Hartwig J T, Larsson D, Silvestrov S D. Deformations of Lie algebras using σ-derivations [J].JAlgebra, 2006, 295(2): 314-361.

[2]Makhlouf A, Silvestrov S D. Hom-algebra structures [J].JGenLieTheory, 2008, 3(2): 51-64.

[3]Makhlouf A, Silvestrov S D. Hom-Lie admissible Hom-coalgebras and Hom-Hopf algebras [C]//GeneralizedLieTheoryinMathematics,PhysicsandBeyond. Berlin:Springer-Verlag, 2009:189-206.

[4]Makhlouf A, Silvestrov S D. Hom-algebras and Hom-coalgebras [J].JAlgebraAppl, 2010, 9(4): 553-589.

[5]Chen Y Y, Wang Z W, Zhang L Y. Quasi-triangular Hom-Lie bialgebras [J].JLieTheory, 2012, 22(4):1075-1089.

[6]Caenepeel S, Goyvaerts I. Monoidal Hom-Hopf algebras [J].CommAlgebra, 2011, 39(6): 2216-2240.

[7]Yau D. The Hom-Yang-Baxter equation, Hom-Lie algebras, and quasi-triangular bialgebras [J].JPhysA, 2009, 42(16): 165202-1-165202-12.

[8]Yau D. Enveloping algebra of Hom-Lie algebras [J].JGenLieTheoryAppl, 2008, 2(2): 95-108.

[9]Wang S X, Wang S H. Hom-Lie algebras in Yetter-Drinfeld categories [J].CommAlgebra, 2014, 42(10): 4540-4561.

[10]Sweedler M E.Hopfalgebras[M]. New York: Benjamin, 1969.

[11]Radford D E. The structure of Hopf algebra with a projection [J].JAlgebra, 1985, 92(2): 322-347.

[12]Wang S H. On the generalizedH-Lie structure of associative algebras in Yetter-Drinfeld categories [J].CommAlgebra, 2002, 30(1): 307-325.

doi:10.3969/j.issn.1003-7985.2015.04.027