面向属性(对象)概念格基于直观图的保并(交)约简
2015-02-27梁新月
梁新月, 万 青, 魏 玲
(西北大学 数学学院,陕西 西安 710127)
·数理科学·
面向属性(对象)概念格基于直观图的保并(交)约简
梁新月, 万 青, 魏 玲
(西北大学 数学学院,陕西 西安 710127)
属性约简是形式概念分析中的一个重要问题, 文中主要研究面向属性概念格和面向对象概念格的保持并(交)不可约元外延不变的约简。给出面向属性概念格和面向对象概念格的保并约简和保交约简的定义; 研究了这两个格的保并约简和保交约简之间的关系; 利用形式背景直观图, 给出获取这两种格的保并约简和保交约简的理论与方法。
面向属性概念格;面向对象概念格;保并约简;保交约简;直观图
形式概念分析理论是由德国数学家Wille于1982年提出来的[1-2], 是一种非常有力的数据分析和知识发现的数学工具, 广泛应用于人工智能和信息检索等领域[3-4]。
粗糙集理论和概念格理论是两种不同的数据分析方法。虽然两种理论有许多不同, 但它们之间存在着诸多相似之处[5], 有很多学者将二者结合起来研究, 以便更好地分析数据和理解数据[5-6]。Duntsch和Gediga 通过定义modal-style算子, 并由粗糙近似算子构造了面向属性概念格[7], Yao Y.Y.借用该思想建立了面向对象概念格, 且证明了面向属性概念格与面向对象概念格的同构[8], 为数据分析提供了新的理论依据。
随着网络的发展, 信息量的增大, 从庞大的数据库中找到我们需要的知识越来越困难, 研究概念格的简化越来越有价值。国内外有关概念格约简的研究已有了一些研究成果。 张文修、魏玲等人研究了形式背景在概念格同构意义下的属性约简理论和方法[9], 王霞等基于概念格的交(并)不可约元分别研究了经典形式背景的概念格、面向对象概念格以及面向属性概念格的属性约简问题[10], 万青、魏玲从对象集的每一个等价类所拥有的属性子集之间的包含关系出发, 构造相应的Hasse图, 直接得到面向属性概念格的并稠密子集[11]。本文从直观图出发, 寻找一种保持面向属性概念格和面向对象概念格的并(交)不可约元外延不变的属性约简, 对概念格结构进行简化, 从而达到简化知识库的目的。
1 理论基础
定义1[1]称三元组(G,M,I)是一个形式背景, 其中G={g1,g2,…,gn}为对象集, 每个gi称为一个对象;M={m1,m2,…,ms}为属性集, 每个mj称为一个属性,I是G和M之间的一个二元关系, 且I⊆G×M。若(g,m)∈I, 则称g具有属性m。
对于形式背景(G,M,I), 在对象子集X⊆G和属性子集B⊆M上分别定义运算*与′[1-2]
X*={m|m∈M,∀g∈X, (g,m)∈I},
B′={g|g∈G,∀m∈B,(g,m)∈I}。
若∀g∈G,g*≠∅,g*≠M, 且∀m∈M,m′≠∅,m′≠G,∀gi,gj,gi*≠gj*,∀mi,mj∈M,mi′≠mj′,则称形式背景(G,M,I)是净化的[2]。本文在有限的净化背景下研究。
设(G,M,I)是形式背景, 在对象集X⊆G及属性集B⊆M上分别定义算子“□”与“”[7-8]
X□={m∈M|m′⊆X},
B□={g∈G|g*⊆B},
X={m∈M|m′∩B≠∅},
B={g∈G|g*∩B≠∅}。
定理1[7-8]设(G,M,I)为形式背景,∀X,X1,X2⊆G及∀B,B1,B2⊆M, 算子“□”与“”有以下性质:
1)X1⊆X2⟹X1□⊆X2□,X1⊆X2;
2)B1⊆B2⟹B1□⊆B2□,B1⊆B2;
3)X⊆X⊆X,B⊆B⊆B;
4)X=X□,X=X,B=B□,B=B;
5) (X1∩X2)□=X1□∩X2□,
(X1∪X2)=X1∪X2,
(B1∩B2)□=B1□∩B2□,
(B1∪B2)=B1∪B2。
Duntsch和Gediga提出了面向属性概念格[7], Yao Y.Y.提出了面向属性概念格[8]。下面给出这两种概念格的定义。
定义2[7]设(G,M,I)为形式背景,∀X⊆G,B⊆M, 满足X=B□且B=X, 则称二元组(X,B)为面向属性概念。其中, 称X为面向属性概念的外延,B为面向属性概念的内涵。通常用LP(G,M,I)表示形式背景(G,M,I)上所有的面向属性概念所组成的集合。
∀(X1,B1),(X2,B2)∈LP(G,M,I), 定义:
(X1,B1)≤(X2,B2)⟺X1⊆X2(⟺B1⊇B2)
则“≤”是LP(G,M,I)上的偏序关系。
在LP(G,M,I)上定义:
(X1,B1)∧(X2,B2)=((X1∩X2), (B1∩B2)),
(X1,B1)∨(X2,B2)=((X1∪X2),B1∪B2),
易知LP(G,M,I)是一个完备格, 称为形式背景(G,M,I)的面向属性概念格。
定义3[8]设(G,M,I)为形式背景, 如果∀X⊆G,B⊆M, 满足X=B且B=X□, 则称二元组(X,B)为面向对象概念。通常用LO(G,M,I)表示形式背景(G,M,I)上所有的面向对象概念所组成的集合。
∀(X1,B1), (X2,B2)∈LO(G,M,I), 定义:
(X1,B1)≤(X2,B2)⟺X1⊆X2(⟺B1⊇B2)
则“≤”是LO(G,M,I)上的偏序关系。
在LO(G,M,I)上定义:
(X1,B1)∧(X2,B2)=((X1∩X2),B1∩B2),
(X1,B1)∨(X2,B2)=((X1∪X2, (B1∪B2)),
易知LO(G,M,I)是一个完备格, 称为形式背景(G,M,I)的面向对象概念格。
设(G,M,I)为形式背景, 称(G,B,IB)为(G,M,I)的子背景,其中IB=I∩G×B。为了叙述简洁, 用“#”统一表示算子*,′,,□。 因此,∀X⊆G,B⊆M,X#B=X#∩B,B#X=B#∩X。
定义4[10]设L是格, 如果x∈L满足以下两个条件:
1)x≠0(L存在0元);
2)∀a,b∈L, 当x=a∨b时, 有x=a或者x=b;
则称元素x∈L是格L的并不可约元。
对偶地, 如果x∈L满足条件:
1)x≠1(L存在单位元1时);
2)∀a,b∈L, 当x=a∧b时, 有x=a或者x=b。
则称元素x是格L的交不可约元。
设(G,M,I)是形式背景,∀B⊆M,记LP(G,B,IB)中所有并不可约元和所有交不可约元分别记为JB(LP)和MB(LP),LO(G,B,IB)中所有并不可约元和所有交不可约元分别记为JB(LO)和MB(LO)。当B=M时, 分别记作J(LP),M(LP),J(LO),M(LO)。记Ext(J(LP))={X|(X,B)∈J(LP)}, Ext(J(LO))={X|(X,B)∈J(LO)};Ext(M(LP))={X|(X,B)∈M(LP)}; Ext(M(LO))={X|(X,B)∈M(LO)}。
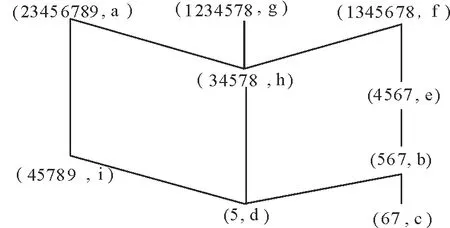
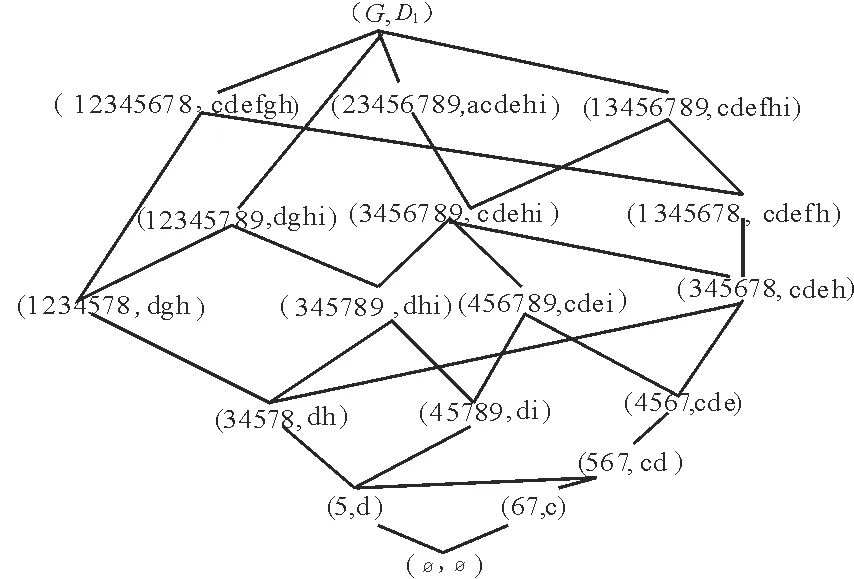
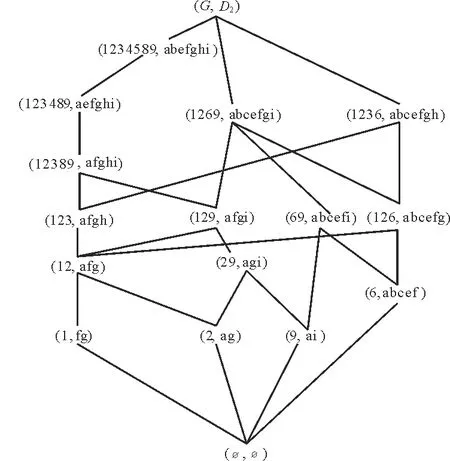
例1 表1是一个形式背景(G,M,I)。对象集G={1, 2, 3, 4, 5, 6, 7, 8, 9}, 属性集M={a, b, c, d, e, f, g, h, i}。该背景的面向属性概念格LP(G,M,I)和面向对象概念格LO(G,M,I)分别如图1和图2所示。
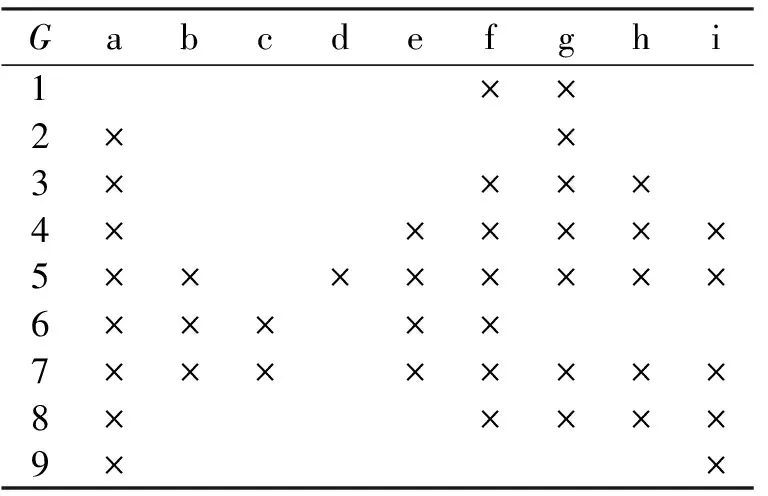
表1 形式背景(G, M, I)Tab.1 (G, M, I)
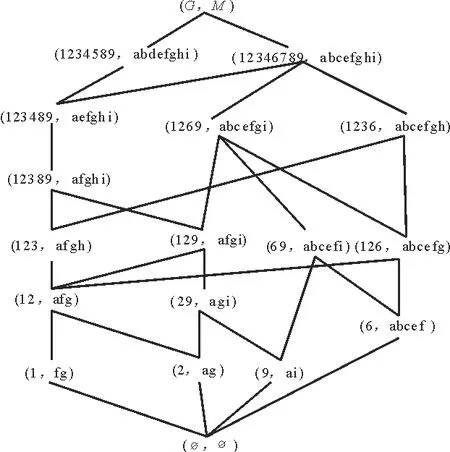
图1 LP(G,M,I)Fig.1 LP(G,M,I)
Ext(J(LP))={{1,2,3,4,5,8,9},{1,2,3,4,8,9},{1,2,3}{1},{2},{6},{9}},
Ext(M(LP))={{1,2,3,4,5,8,9},{1,2,3,4,6,7,8,9},{1,2,3,8,9},{1,2,6,9},{1,2,3,6},{6,9}{2,9},{1}},
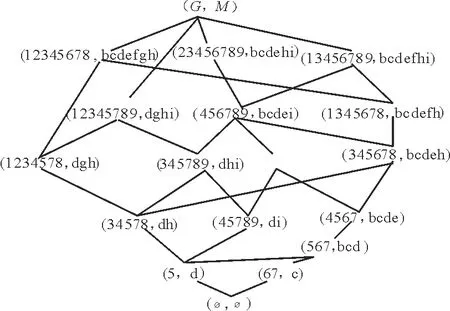
图2 LO(G,M,I)Fig.2 LO(G,M,I)
Ext(J(LO))={{2,3,4,5,6,7,8,9},{1,3,4,5,6,7,8}{1,2,3,4,5,7,8}{3,4,5,7,8}{4,5,7,8,9},{4,5,6,7},{6,7},{5}},
Ext(M(LO))={{1,2,3,4,5,6,7,8},{2,3,4,5,6,7,8,9},{1,3,4,5,6,7,8,9},{1,2,3,4,5,7,8,9},{4,5,6,7,8,9},{5,6,7},{6,7}}。
2 面向属性(对象)概念格的保并(交)约简
2.1 基本定义和相关性质
本节给出面向属性(对象)概念格保并、保交约简定义, 并利用这两种格之间的关系研究保并、保交约简之间的关系。
定义5 设(G,M,I)为形式背景, 若存在属性集B⊆M, 使得Ext(JB(LP))=Ext(J(LP)), 则称B是面向属性概念格LP(G,M,I)的保并协调集; 若∀b∈B,Ext(JB-{b}(LP))≠Ext(J(LP)), 则称B为LP(G,M,I)的保并约简。将LP(G,M,I)的所有保并约简记为Red(JP)。
类似地,可定义面向对象概念格的保并约简。若存在属性集B⊆M, 使得Ext(JB(LO))=Ext(J(LO)), 则称B是面向对象概念格LO(G,M,I)的保并协调集;若∀b∈B, Ext(JB-{b}(LO))≠Ext(J(LO)), 则称B为LO(G,M,I)的保并约简。将LO(G,M,I)的所有保并约简记为Red(JO)。
定义6 设(G,M,I)为形式背景, 若存在属性集B⊆M, 使得Ext(MB(LP))=Ext(M(LP)), 则称B是面向属性概念格LP(G,M,I)的保交协调集; 若∀b∈B, Ext(MB-{b}(LP))≠Ext(M(LP)), 则称B为LP(G,M,I)的保交约简。将LP(G,M,I)的所有保交约简记为Red(MP)。
类似地,可定义面向对象概念格的保交约简。若存在属性集B⊆M, 使得Ext(MB(LO))=Ext(M(LO)), 则称B是面向对象概念格LO(G,M,I)的保交协调集; 若∀b∈B, Ext(MB-{b}(LO))≠Ext(M(LO)) 则称B为LO(G,M,I)的保交约简。将LO(G,M,I)的所有保交约简记为Red(MO)。
定理2 设(G,M,I)为形式背景,则有:
1) Red(MP)=Red(JO);
2) Red(JP)=Red(MO)。
证 明 ∀(X,B)∈LP(G,M,I)
有(XC,BC)∈LO(G,M,I)。
又因为LP(G,M,I)≌LO(G,M,I),∀B⊆M, 有
Ext(M(LP))={Xi|(Xi,Bi)∈M(LP)},
Ext(J(LO))={XiC|(Xi,Bi)∈M(LP)},
Ext(MB(LP))={Xj|(Xj,Bj)∈MB(LP)},
Ext(JB(LO))={XjC|(Xj,Bj)∈MB(LP)}。
若B∈Red(MP), 则Ext(M(LP))=Ext(MB(LP))。故Ext(J(LO))=Ext(JB(LO)), 所以B∈Red(JO)。
类似地,∀B∈Red(JO), 有B∈Red(MP)。
综上得Red(MP)=Red(JO)。
同理可证Red(JP)=Red(MO)。
2.2 基于直观图的面向属性(对象)概念格的保并(交)约简
本节依据文献[11], 定义了直观图, 并给出了寻找面向属性(对象)概念格的保交、保并约简。
定义7[11]设(G,M,I)为形式背景, 记R={(gi,gj)|gi*=gj*,∀gi,gj∈G},HG={([g]R,g*)|g∈G, [g]R∈G/R1}。显然,R1是G上的等价关系,定义([g1]R,g1*)≤([g2]R,g2*)⟺g1*⊂g2*, 则“≤”为HG上的偏序关系, 因此可得到Hasse图(HG,≤), 我们称其为(G,M,I)的对象直观图。
类似地,可定义(G,M,I)的属性直观图(HM, ≤)。 记P={(ms,mt)|(ms′=mt′,∀ms,mt∈M},HM={(m′,[m]P|m∈M, [m]P∈M/P}。显然,P是M上的等价关系, 定义([m1]P,m1′)≤([m2]P,m2′)⟺m1′⊂m2′, “≤”为HM上的偏序关系。
由于本文的形式背景都是净化的, 则HG={(g,g*)|g∈G},HM={(m′,m)|m∈M}。记min(HG)为HG的极小元, min(HM)为HM的极小元。
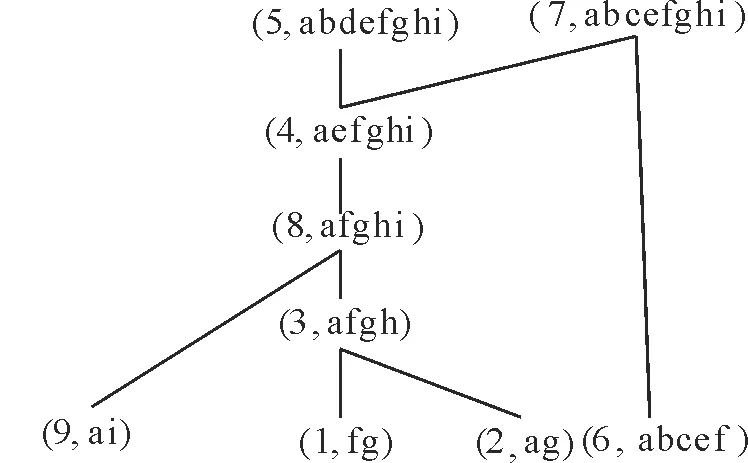
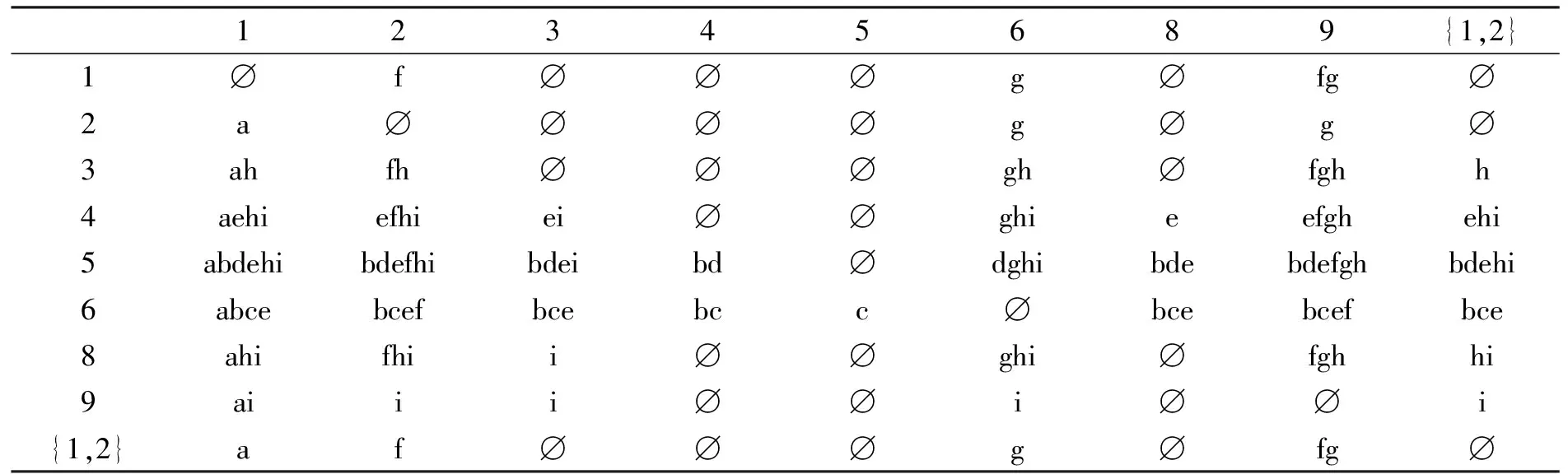
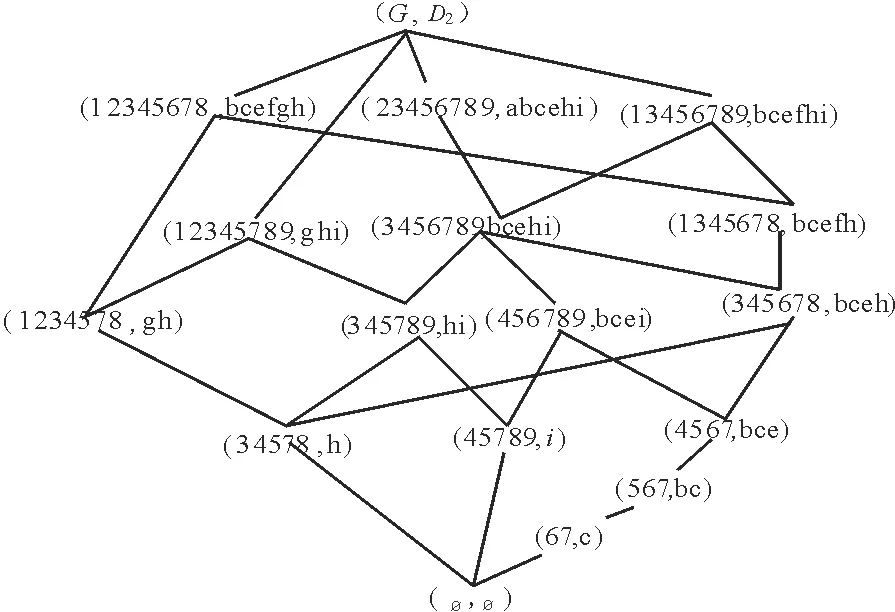
定义8[12]∀a,b, 若a 定理3 设(G,M,I)是形式背景, (HG,≤)为该形式背景的对象直观图,∀g∈G, 有以下结论: 2) min(HG)⊆J(LP); 3) (g,g*)∉min(HG)且满足g*-∪i∈τgi*≠∅, 则(g,g)∈J(LP)。其中(gi,gi*)(g,g*)。 证 明 1)由于(g,g)∈LP(G,M,I), 我们只需要证为单点集, 由算子的定义可得g=g*。由于gi*⊆g*, 则有g={x∈G|x*⊆g=g*}=∪i∈τgi。综上有 2)设(g,g*)∈min(HG), 由1)有(g,g*)∈LP(G,M,I)。由定义8,∀(g,g*)∈min(HG), 不存在gi∈G使得gi*⊂g*。因此,g*≠∪{gi*|gi*⊂g*,∀gi∈G}。因此, min(HG)⊆J(LP)得证。 对偶的, (HM,≤)为该形式背景的属性直观图, 则有以下定理。 定理4 ∀m∈M, 有以下结论 2) min(HM)⊆J(LO); 3) (m′,m)∉min(HM)且满足m′-∪s∈Sms′≠∅, 则(m,m)∈J(LO)。其中(ms′,ms)(m′,m)。 定理5 设(G,M,I)是形式背景, (HM,≤)为其属性直观图, 记D={m∈G|(m′,m)∈min(HM)∨(m′,m) ∉min(HM)⟹m′-∪s∈Sms′≠∅, (ms′,ms)(m′,m)},则Red(JO)={D}。 证 明 若取Ic=G×MI, 称(G,M,Ic)为(G,M,I)的补背景, 相应的格记为Lc, 保持其概念格结构不变的约简记为Red(Lc), 保交约简为Red(Mc)。由文献[13]可得Red(LP)=Red(Lc),∀(X,B)∈LP(G,M,I), 有(X,BC)∈Lc(G,M,I),则LP(G,M,I)和Lc(G,M,I)有相同的偏序关系。因此, Red(MP)=Red(Mc), 而Red(Lc)=Red(Mc), Red(MP)=Red(JO)。所以Red(JO)=Red(Lc)。 结合定理5, 可知Red(MP)=Red(JO)={D}。 即从属性直观图直接可得到面向对象概念格的保并约简和面向属性概念格的保交约简。 例2 对于表1形式背景, 求其面向对象概念格的保并约简和面向属性概念格的保交约简。 图3 (HM≤)Fig.3 LO(G,M,I) 图3是表1对应的属性直观图, 根据D的定义, 逐一验证属性特点可得D={a,c,d,e,f,g,h,i}。则Red(MP)=Red(JO)={D}。其相应的面向属性概念格和面向对象概念格分别如图4, 图5所示。属性集D保持面向属性概念格的交不可约元外延不变, 保持面向对象概念格的并不可约元的外延不变。 图4 LP(G,D,ID)Fig.4 LP(G,D,ID) 图5 LO(G,D,ID)Fig.5 LO(G,D,ID) 记J(HG)={{g}|(g,g)∈J(LP)}。L={Lg|Lg=∪i∈τgi, (gi,gi*)(g,g*)且{g}∈J(HG)min(HG)},F =LJ(HG),E =J(HG)∪F 。 引理1 设(G,M,I)为形式背景(HG,≤)为其属性直观图。若存在{g}∈J(HG), 有Lg∈L且|Lg|>1,则Lg=∪i∈τgi, 其中(gi,gi*)(g,g*)。 证 明 不失一般性,假设Lg={g1,g2}。由算子的定义和性质可得Lg=g1∪g2。Lg={gi|gi*⊆g1*∪g2*}={gi|gi*⊆g1*∪g2*}。由于(gi,gi*)(g,g*), 则不存在gj使得gj≠gi有gj*⊆g1*∪g2*,gj*g1*,gj*g2*。因此Lg=∪i∈τgig□。 引理2 设(G,M,I)为形式背景,B是面向属性概念格的保并协调集,则∀Lg∈L, 有Lg≠g。 证 明 由于B是面向属性概念格的保并协调集,∀{g}∈J(HG), 有g=g且{g}∈JB(HG)。∀Lg∈L,由L的定义知,Lg=∪i∈τgi, 其中(gi,gi*)(g,g*)。因为(gi,gi)∈LP(G,M,I), 所以gi=∪j∈Jgij,其中gij∈J(HG); 当gi∈J(HG)时,gij=gi。由Lg=∪i∈τgi, 则Lg=∪i∈τgi,两边同时交B, 有Lg=∪i∈τgi。由gi=∪j∈Jgij有gi=∪j∈Jgij,故Lg=∪i∈τ(∪j∈Jgij)。假设g=Lg,于是有g=∪i∈τ(∪j∈Jgij), 故g-∪i∈τ(∪j∈Jgij)=∅。由gi=gi*⊂g*=g,gi=∪j∈Jgij,则gij⊆gi⊂g,故gij≠g, 又由gij∈J(HG),g∈J(HG),故gij≠g。因为B是面向属性概念格的保并协调集, 则有gij=gij,g=g,gij≠g。故gij≠g, 又由于gij⊂g,则gij⊆g, 故gij⊂g。于是gij*B⊂g*B。因此对于(gk,gk*B)(g,g*B), 一定有∪i∈τ(∪j∈Jgij*B)⊆∪k∈Kgk*B, 则有g*B-∪k∈Kgk*B⊆g*B-∪i∈τ(∪j∈Jgij*B)=∅, 由定理3知{g}∉JB(HG), 此与{g}∈JB(HG)矛盾。故Lg≠g。 定理6 设(G,M,I)为形式背景,B是面向属性概念格的保并协调集⟺∀E∈E 有E=E。 证 明 必要性。由E∈E , 则E∈J(HG)或E∈F 。 当E∈J(HG)时, 由于B是面向属性概念格的保并协调集, 则E=E。 当E∈F 时, 则存在Lg, 使得E=Lg=∪i∈τgi, (gi,gi*)(g,g*)且g*-∪i∈τgi*≠∅。由引理1可知Lg=∪i∈τgi。由定理3中1)可得gi=∪j∈Jgij, 其中gij*⊆gi*。故Lg=∪i∈τ(∪j∈Jgij)。由算子的定义有Lg={gk|gk*B⊆Lg}={gk|gk*B⊆∪i∈τgi}。对于上述任意的gij, 由于gij*⊆gi*⊂g*。则gij*B⊆g*B=g。 由gij的任意性知,Lg⊆Lg。即E⊆E。假设E≠E, 即Lg≠Lg。则存在gk∈Lg, 且gk∉Lg。由g=g∪(∪i∈τ(∪j∈Jgij))=g∪Lg,则ggg=g∪Lg, 故gk=g或gk∈Lg。由于gk∉Lg, 从而gk=g。所以gk*B=g*B=g。由于gk*B⊆Lg⊆g, 故Lg=g。由引理2知,当B是面向属性概念格的保并协调集时,Lg≠g。故矛盾。从而E=E。综上,∀E∈E 有E=E。 充分性。要证明B是面向属性概念格的保并协调集, 即证∀{g}∈J(HG), 有g=g且{g}∈JB(HG)。由于J(HG)⊆E ,故∀{g}∈J(HG), 有g=g。下证{g}∈JB(HG)。因为∀{g}∈J(HG), 有(g,g*)∈ min(HG)或(g,g*)∉min(HG)且满足g*-∪i∈τgi*≠∅, 其中(gi,gi*)(g,g*)。 当(g,g*)∈min(HG)时, (g,g)=(g,g*)∈J(LP), 由于g=g, 则(g,g)=(g,g*B), 故{g}∈JB(HG)。 当(g,g*)∉min(HG)时,g*-∪i∈τgi*≠∅, 其中(gi,gi*)(g,g*)。由于Lg=∪i∈τgi, 则Lg=∪i∈τgi*。因此g*-Lg≠∅, 故Lg⊂g=g*。由于g=g∪(∪i∈τgi)且{g}∈J(HG), 由引理1可得g=g∪Lg,g∉Lg。又由于g=g,Lg=Lg, 则g=g∪Lg且g∉Lg。即不存在gj, 满足(gj,gj*)≤(g,g*), 使得gj*B=g*B。因此g∉∪k∈Kgk且g=g∪(∪k∈Kgk), 其中(gk,gk*B)(g,g*B)。又g=g∪Lg且g∉Lg, 故Lg=∪k∈Kgk。从而Lg=∪k∈Kgk。故∅≠g-Lg=g-∪k∈Kgk=g*B-∪k∈Kgk*B。由定理3可得{g}∈JB(HG)。 综上,B是面向属性概念格的保并协调集。 定义9 ∀Ei,Ej∈E , 定义D(Ei,Ej)=Ei-Ej,称∧={D(Ei,Ej)|Ei,Ej∈E }为面向属性概念格的保并辨识属性矩阵。 定理7 设(G,M,I)是形式背景∅≠B⊆M,则下列命题等价: 1)B是面向属性概念格的保并协调集; 2)∀D(Ei,Ej)≠∅, 有B∩D(Ei,Ej)≠∅; 3)∀C⊆M,C∩B≠∅, 则C∉L。 证 明 1)⟹2) 若B是面向属性概念格的保并约简, 由定理6知:∀E∈E ,E=E。要证B∩D(Ei,Ej)≠∅, 即证Ei-Ej≠∅。假设Ei-Ej=∅, 则Ei⊆Ej, 于是有Ei⊆Ej。又因为Ei=Ei,Ej=Ej, 所以Ei⊆Ej, 故Ei⊆Ej, 这与D(Ei,Ej)≠∅矛盾。即有B∩D(Ei,Ej)≠∅。 2)⟹1) 假设B不是面向属性概念格的保并协调集, 则存在E∈E ,E≠E,即存在g∈G, 使得g∈E,g∉E或g∉E,g∈E。若g∈Eg∉E, 则有g⊆E,所以B∩D({g},E)=∅, 与已知条件矛盾。若g∉E,g∈E, 则有gE,g⊆EB∩D({g},E)≠∅,D({g},E)=∅。由D({g},E)=∅, 则B∩D({g},E)=∅。这与B∩D({g},E)≠∅矛盾, 故B是面向属性概念格的保并协调集。 2)⟺3) 显然成立。 定义10 设(G,M,I)是形式背景, 定义 M=∧{∨D(Ei,Ej)|D(Ei,Ej)∈L,D(Ei,Ej)≠∅} 称M为面向属性概念格的保并辨识属性函数。这里∧,∨分别表示合取和析取。 定理8 设(G,M,I)是形式背景∅≠D⊆M,则D是面向属性概念格的保并约简, 当且仅当∧aj∈Daj是M的最小析取范式的一个析取支。 证 明 由定理7和差别函数中最小析取范式形成的定义直接得到。 例1 对于表1的形式背景, 图6为其对象直观图。判定其面向属性概念格的保并约简和面向对象概念格的保交约简。 图6 (HG≤)Fig.6 (HG≤) 由图6,逐一验证得到E ={{1}, {2}, {3}, {4}, {5}, {6}, {8}, {9}, {1,2}}。 表2是由定义9得到的面向属性概念格的保并辨识矩阵。 表2 LP(G,M,I)保并辨识矩阵表Tab.2 LP(G,M,I) 通过表2可以得到面向属性概念格的保并辨识属性函数: M=(a∧c∧e∧f∧g∧h∧i∧b)∨(a∧c∧e∧f∧g∧h∧i∧d)。 根据定理8,面向属性概念格的保并约简集:D1={a, c, d, e, f, g, h, i},D2={a, b, c, e, f, g, h, i}。则Red(MO)=Red(JP)={D1,D2},当约简为D1时, 其对应背景的面向属性概念格为图4, 其对应的属性概念格为图5。当约简为D2时, 图7为其对应背景的面向属性概念格, 图8为其面向对象概念格。 图7 LP(G,D2,ID2)Fig.7 LP(G,D2,ID2) 图8 LO(G,D2,ID2)Fig.8 LO(G,D2,ID2) 概念格作为一种概念数据分析和知识处理的数学工具, 已被广泛应用于众多领域。本文主要基于直观图寻找面向属性(对象)概念格的保并(交)约简方法。由于不可约元在概念格中非常重要, 利用直观图减化了求约简的过程, 并最终实现对面向属性(对象)概念格的简化。该方法避免了画出格图, 简化了找约简的过程, 从而也反应了这两种格之间的联系。进一步的, 我们还可以通过直观图找这两种格的粒约简, 并研究这三种约简之间的关系。 [1]WILLER.Restructuringlatticetheory:anapproachbasedonhierarchiesofconcepts[C].RIVALI(Ed.),OrderedSets.Dordrecht:Reidel, 1982:445-470. [2]GANTERB,WILLER.FormalConceptAnalysis[M].NewYork:MathematicalFoundations.Springer-Verlag, 1999. [3]CARPINETOC,ROMANOG.Alatticeconceptualclusteringsystemanditsapplicationtobrowsingretrieval[J].MachineLearning, 1996, 10: 95-122. [4]CHENYH,YAOYY.Amultiviewapproachforintelligentdataanalysisbasedondataoperators[J].InformationSciences,2008, 178(1):1-20. [5]KENTRE.Roughconceptanalysis:asynthesisofroughsetsandformalconceptanalysis[J].FundamentaInformaticae, 1996, 27: 169-181. [6]HUKY,SUIYF,LUYC,etal.Conceptapproximationinconceptlattice[J].LectureNotesinComputerScience, 2001, 20(35):167-173. [7]DUNTSCHI,GEDIGAG.Approximationoperatorsinqualitativedataanalysis[C]//TheoryandApplicationofRelationalStructuresasKnowledgeInstruments.Heidelberg:Springer, 2003. [8]YAOYY.Acomparativestudyofformalconceptanalysisandroughsettheoryindataanalysis[J].LectureNotesinArtificialIntelligence, 2004, 3066: 59-68. [9] 张文修, 魏玲, 祁建军, 概念格的属性约简理论与方法[J].中国科学(E辑信息科学), 2005, 35(6);628-639. [10] 王霞. 概念格约简理论与方法[D].西安:西安交通大学, 2008. [11] 万青, 李涛, 魏玲, 一种基于并不可约元的建格新方法[J].西北大学学报(自然科学版), 2013, 43(1):10-14. [12]DAVEYBA,PRIESTLEYHA.IntroductiontoLatticesandOrder[M].Cambridge:CambridgeUniversityPress, 2002. [13]MEDINAJ.Relatingattributereductioninformal,object-orientedandproperty-orientedconceptlattices[J].ComputersandMathematicswithApplication,2012,64:1990-2002. (编 辑亢小玉) MIE-preserving reduction and JIE-preserving reduction of property(object)-oriented concept lattices based on the pictorial diagram LIANG Xin-yue,WAN Qing, WEI Ling (School of Mathematics, Northwest University, Xi′an 710127, China) Attribute reduction is an important issue in formal concept analysis. This paper mainly studies MIE(meet irreducible element)-preserving reduction and JIE(join irreducible element)-preserving reduction of property-oriented and object-oriented concept lattices. Firstly, the definitions of MIE-preserving reduction and JIE-preserving reduction of property-oriented and object-oriented concept lattices are given. Then, the relationship between MIE(JIE)-preserving reduction in property-oriented and its counterpart in object-oriented concept lattices is presented. Finally, pictorial diagram is used to give the theory and method of finding the MIE-preserving reduction and JIE-preserving reduction. attribute-oriented concept lattices; object-oriented concept lattices; MIE-preserving reduction; JIE-preserving reduction; pictorial diagram 2014-04-17 国家自然科学基金资助项目(11371014,11071281) 梁新月,女,陕西西安人,从事形式概念分析、粗糙集理论研究。 魏玲,女,陕西西安人,教授,博士生导师,从事形式概念分析、粗糙集理论、概率论等研究。 TP18;O29 :ADOI:10.16152/j.cnki.xdxbzr.2015-03-003
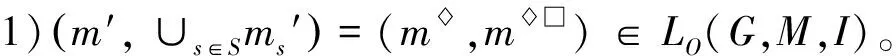


3 结 语
