朴丽莎，葛仁东

(1.云南大学 滇池学院，云南 昆明650228;2.大连民族大学 理学院，辽宁 大连116605)

理解和应用低维低阶的数学结论是较为容易的，但由于处理实际问题的复杂性，往往需要使用高维空间或高阶的数学结论。本文以Bézier 曲线为例，提出合理对称模式直接扩展的新方法，即借助Bézier 曲线低阶对称矩阵形式的方程，通过二项式定理的展开式系数找寻规律，直接扩展到高阶方程情形，进而建立了n 阶Bézier 曲线方程，并对扩展结果予以证明。另外，通过举例说明了数学学科中也存在很多类似的结论。

1 Bézier 曲线的合理扩展

Bézier 曲线是计算机辅助几何设计中最常用的曲线之一，是由法国雷诺汽车公司的工程师Bézier 在上世纪60 年代提出的。该方法采用折线组成的多边形来定义一条曲线，设计者先用折线多边形描绘这条曲线的大致轮廓，再用Bézier 曲线表达式产生一条光滑的曲线［1］。

Bézier 曲线有不同的数学定义形式，如de Casteljau 递归算法、Bernstein 多项式基函数，其中用控制顶点定义的Bernstein 基［2］表示形式容易理解，且应用广泛，本文将针对该参数多项式形式进行方程的建立和结论的证明。

1.1 Bézier 曲线的建立

由两点p0，p1可以确定一条一次Bézier 曲线，方程为p(t)=p0+(p1－p0)t，t∈［0，1］。为了找到比较容易扩展的对称式曲线方程，根据文献［3］可以将方程改写成如下矩阵形式:

式中，B0，1(t)=1 － t，B1，1(t)=t，记M=是对称矩阵。

用此方法继续写出三点二次Bézier 曲线方程，进而扩展n 次方程。由p0，p1，p2确定的二次Bézier 曲线为

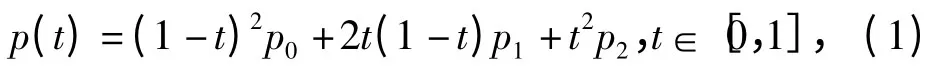
令

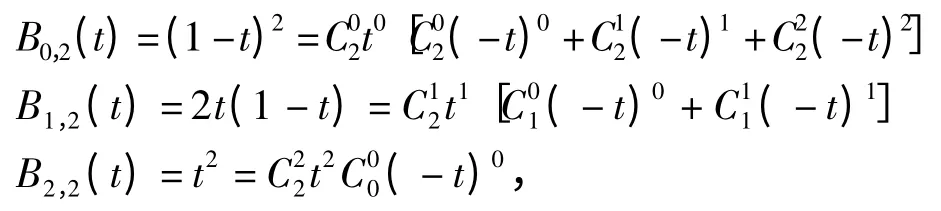
则式(1)可改写成

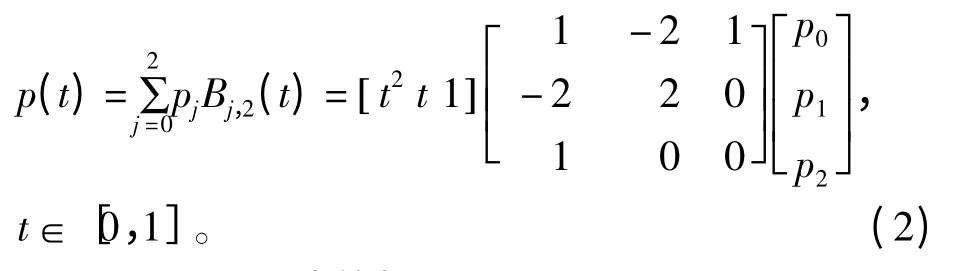
1.2 Bézier 曲线的扩展及证明

由前小节的分析可得如下结论。

定理 式(1)和式(2)对称矩阵中的元素依次为二项式［(1 － t)+ t］n展开式中关于t 的系数，故可直接将对称矩阵扩展进而得到n 次Bézier曲线方程

证明 要证明Bézier 曲线可表示成式(3)，即证明

Mn+1=(bi+1，j+1)n+1是n+1 阶对称方阵

因为

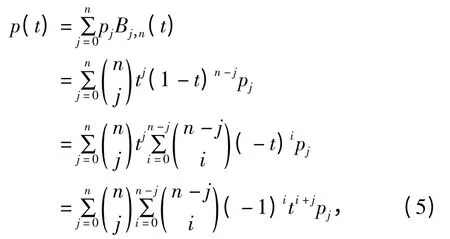
令i+j=s，则式(5)

故有

当0 ≤i + j ≤n 时，bi+1，j+1=(－ 1)n－i－j=(－1)n－i－j。

证毕。

上述分析说明，对于复杂的数学结论，如果可以找到合理的对称形式，就存在向高阶高维扩展的可能性，并且由直接扩展得到的结论从形式上呈现对称性，内容上规律性、紧凑性强，这些优点更有利于数学结论的理解和应用。接下来给出直线方程问题和函数插值问题，说明合理扩展对称式方程这一方法的一般性。

2 举 例

2.1 由平面直线到空间直线

在平面上任取两点(x1，y1)和(x2，y2)，两点所确定的直线斜率k=(x2≠x1)，故点斜式方程y－y1=k(x－x1)。将方程改写为对称式

设想由平面到空间，也就是二维扩展到三维，具体到每一个点，原有的坐标分量由2 个变成3个。那么，根据前文的合理扩展想法，平面对称式方程(4)就可以直接扩展为由空间两点(x1，y1，z1)和(x2，y2，z2)确定的直线方程

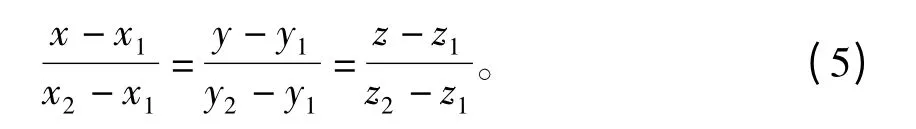
对式(5)的验证详见文献［4］。

2.2 由一阶插值到高阶插值

插值法是在生产实践中提炼而成的方法，主要是通过离散样本点作一条通过这些点的光滑曲线，以便满足设计要求或进行加工。

以Lagrange 插值多项式为例，设两个节点(x0，y0)，(x1，y1)则可以确定一次插值多项L1(x)=a0+a1x，由插值条件

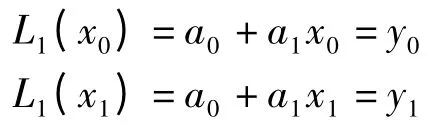
可以联立解出待定参数a0=。

所以，两个节点的一次插值多项式为L1(x)=。

将其改写成如下对称形式:

不难发现两个线性函数满足

也就是li(x)(i=0，1)在对应的插值点xi处取值为1，在其他节点处取值为0。由此，可以设想通过扩展li(x)进而将式(6)扩展成高阶插值。那么n+1 个节点的n 次插值多项式的形式为

由此说明li(x)(i=0，1，...，n)的存在性进而证明式(7)扩展的合理性。n 次多项式li(x)(i=0，1，...，n)满足li(xj)=，有n 个根xj(j=0，1，...，n，j≠i)，且li(xi)=1，故它必定如下形式:

代入式(7)后可以证明Ln(x)满足插值条件［5］。

3 结 语

本文主要通过建立并扩展Bézier 曲线的对称矩阵式方程，提出了复杂数学结论可以借助合理对称形式向高阶高维扩展的方法。另外，通过直线方程和函数插值的举例验证了数学中确实存在一些对称式结论可以直接进行合理扩展，并且扩展得到的结论更有助于理解和应用。相信在数学学科中，还有很多这样的例子。但是，并不是所有的对称式结论都可以扩展，在接下来的研究中对称形式的数学结论可以扩展的条件和适用范围将是亟待解决的问题。

［1］顾兰智，方忆湘. Bézier 曲线绘制程序的开发［J］. 电脑开发应用，2008(9):34 －35.

［2］何援军.几何计算［M］.2 版.北京:高等教育出版社，2013:301 －330.

［3］葛仁东，张艳茹，赵玲玲，等. 体育馆顶部外形设计的数值模拟［J］.大连民族学院学报，2009(1):27 －29.

［4］吕林根，许子道.解析几何［M］.4 版.北京:高等教育出版社，2006:112 －119.

［5］丁丽娟，程杞元.数值计算方法［M］.2 版.北京:北京理工大学出版社，2011:101 －106.