张治海，王善坤，李 阳

(大连理工大学 城市学院，辽宁 大连116024)

在组合学中，组合序列的对数凸性是基本的研究课题之一。设{an}n≥0是非负无限实数序列，若对于任意的n≥1 都有

成立，则称该序列是凸的(凹的)。若对于任意的n≥1 都有

成立，则称该序列是对数凸的(对数凹的)。许多著名的组合序列都是对数凸的。组合序列的对数凸性与组合序列的对数凹性、TP 矩阵、PF 序列等密切相关。本文研究带有参数的组合序列广义中心三项式系数的对数凸性。

1 广义中心三项式系数及相关工具简介

1.1 广义中心三项式系数

中心三项式系数Tn定义为三项式(x2+x +1)n展开式中xn的系数［1］。由多项式定理可以得出它的显式表达式为

中心三项式系数Tn在计数组合学中表示从点(0，0)到点(n，0)仅使用(1，0)，(1，1)，(1，-1)步的格路数。

Sun［2］在研究组合序列的同余性质时引入了广义中心三项式系数Tn(b，c)，其定义为三项式(x2+bx+c)n中xn的系数，即

式中，b，c 为非负整数。由于

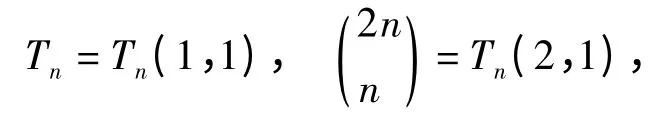
因此广义中心三项式系数Tn(b，c)可以看成是中心三项式系数及中心二项式系数的一般化。Wilf［3］给出了广义中心三项式系数Tn的发生函数

由此可以得到递归关系［4］

1.2 Riordan 矩阵

Riordan 矩阵是无限下三角矩阵，该矩阵可以用一对函数(g(x)，f(x))来表示。Riordan 矩阵第k 列元素的发生函数Ck(x)为

式中，g(0)=1，f(0)≠0。

设R=［rn，k］n，k≥0为Riordan 矩阵，且R=(g(x)，f(x))，则Riordan 矩阵R 可以通过序列A={an}n≥0和Z={zn}n≥0来刻画，即

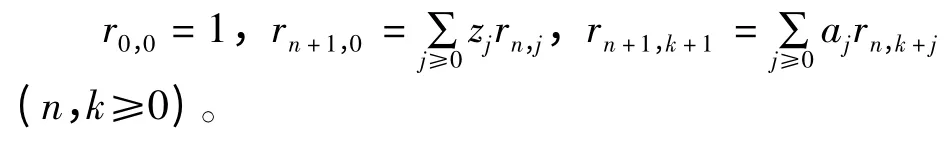
设A 序列的发生函数为A(x)，Z 序列的发生函数为Z(x)，则A(x)和Z(x)与g(x)和f(x)满足关系

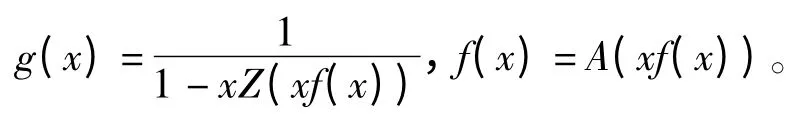
1.3 Aigner-Catalan-Riordan 矩阵

设矩阵

是无限下三角矩阵，其满足递归关系

式中，zj，aj，k为非负整数，且当k ＞j≥0 时aj，k=0。无限下三角矩阵T=［tn，k］n，k≥0称为Aigner -Catalan-Riordan 矩阵。

设矩阵T=［tn，k］n，k≥0为Aigner - Catalan -Riordan 矩阵，则称矩阵

为Aigner-Catalan-Riordan 矩阵T=［tn，k］n，k≥0的系数矩阵。容易看出Aigner-Catalan-Riordan 矩阵是广义的Riordan 矩阵。

2 广义中心三项式系数的对数凸性

定义1 广义中心三项式三角矩阵T(b，c)=［Tn，k(b，c)］n，k≥0是无限下三角矩阵，其递归定义为

式中，b，c 为非负整数。

定理1 广义中心三项式系数Tn(b，c)是广义中心三项式三角矩阵T(b，c)=［Tn，k(b，c)］n，k≥0的第0 列元素。

证明 由Riordan 矩阵的定义可得广义中心三项式三角矩阵T(b，c)=［Tn，k(b，c)］n，k≥0是Riordan 矩阵的特例，且其A 序列与Z 序列分别为

其A 序列与Z 序列的发生函数分别为

设T(b，c)=(g(x)，f(x))，则由A(x)和Z(x)与g(x)和f(x)之间满足的关系可得

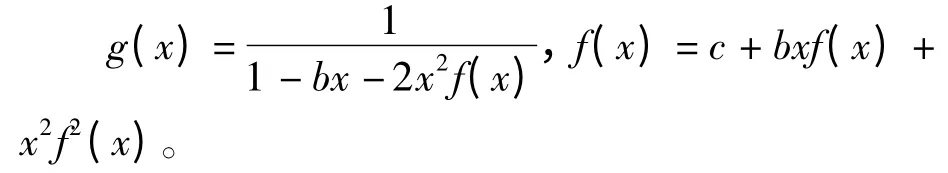
由f(0)=c 可以解得

将式g(x)与广义中心三项式系数的发生函数进行比较，可得广义中心三项式系数Tn(b，c)是广义中心三项式三角矩阵T(b，c)=［Tn，k(b，c)］n，k≥0的第0 列元素，即

证毕。

定理2［5］设矩阵T=［tn，k］n，k≥0为Aigner -Catalan-Riordan 矩阵，若该矩阵的系数矩阵［ζ，A］是TP2矩阵，则矩阵T 的第0 列元素构成对数凸序列。

证明 由广义中心三项式三角矩阵T(b，c)=［Tn，k(b，c)］n，k≥0的定义可得矩阵T(b，c)是Aigner-Catalan-Riordan 矩阵的特例，其系数矩阵为

易见当b2≥2c 时系数矩阵［ζ，A］是TP2矩阵。最后由定理2 可得当b≥时，广义中心三项式系数Tn(b，c)构成对数凸序列。

证毕。

Zhu［6］对广义中心三项式系数的对数凸性进行过研究，并且得出过以下定理。

定理4［6］当b≥时，广义中心三项式系数Tn(b，c)构成对数凸序列。

3 应 用

许多组合计数问题中都会出现中心Delannoy数Dn［7］，其定义为［8］

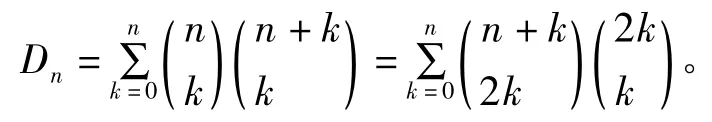
中心Delannoy 数Dn的组合解释为从点(0，0)到点(n，n)仅使用步(1，0)，(0，1)及(1，1)的格路数。中心Delannoy 数Dn还满足递归关系

可以看出，从中心Delannoy 数Dn的定义出发判定该数是否具有对数凸性不是一件容易的事。但是由中心Delannoy 数Dn及广义中心三项式系数Tn(b，c)的定义可得Dn=Tn(3，2)。因此可以立即得到以下推论。

推论1 中心Delannoy 数构成对数凸序列。

在前文中简介过中心二项式系数也是广义中心三项式系数的特例，因此可以立即得到关于中心二项式系数对数凸性的推论。

推论2 中心二项式系数构成对数凸序列。

4 结 语

通过将广义中心三项式系数内嵌于广义中心三项式三角矩阵中，并借助TP 理论对广义中心三项式系数进行研究，加强和推广了Zhu 的结论。作为应用，统一的给出中心Delannoy 数和中心二项式系数各自都构成对数凸序列的结果。

广义中心三项式系数可以表示以中心二项式系数、中心三项式系数及中心Delannoy 数为代表的一类组合序列。而Colored -Motzkin 数可以表示以Catalan 数、Motzkin 数、Hexagonal 数为代表的一类组合序列。或许可以模仿研究广义中心三项式系数对数凸性的方法逆向构造三角矩阵来研究Colored-Motzkin 数的对数凸性。

［1］ANDREWS G E. Euler’s“exemplum memorabile inductionis fallacis”and q - trinomial coefficients［J］. J. Amer. Math. Soc.，1990，3(3):653 -669.

［2］SUN Z W. Congruences involving generalized central trinomial coefficients［J］. Sci. China Math.，2014，57(7):1375 -1400.

［3］WILF H S. Generatingfunctionology［M］. Boston MA :Academic Press，Inc.，1990.

［4］NOE T D. On the divisibility of generalized central trinomial coefficients［J］. J. Integer Seq.，2006，9(2):Article 06.2.7，12.

［5］WANG Y，ZHANG Z H. Log - convexity of Aigner -Catalan -Riordan numbers［J］. Linear Algebra Appl.，2014，463:45 -55.

［6］ZHU B X. Log-convexity and strong q-log-convexity for some triangular arrays［J］. Adv. in Appl. Math.，2013，50(4):595 -606.

［7］SUN Z H. Congruences concerning Legendre polynomials［J］.Proc. Amer. Math. Soc.，2011，139(6):1915-1929.

［8］CAUGHMAN J S，HAITHCOCK C R，VEERMAN J J P.A note on lattice chains and Delannoy numbers［J］. Discrete Math.，2008，308(12):2623 -2628.