林永晖

（永春县教育局，福建泉州 362600）

数学问题的设计与学生创新思维能力的培养①

林永晖

（永春县教育局，福建泉州 362600）

设计新颖且具有挑战性的数学问题，有利于培养学生的创新思维能力。在数学教学中，根据学生的认识水平、教材内容、课型要求，通过设计趣味型问题、开放型问题、互逆型问题、迷惑型问题、联想型问题、探索型问题、应用型问题、延展型问题等，让学生去思考、探索，在思维活动中进行创新，多方面培养学生的创新思维能力。

数学问题;创新思维;能力培养

创新依赖于具有创造力的人才，人才依赖于教育。为了培养学生的创新思维能力，必须设置适当的问题，让学生去思考、探索，在思维活动中得以创新。在数学课堂教学中，应根据学生的认识水平以及教学内容设计有针对性的数学问题［1］，通过问题的解决达到培养学生创新思维能力的目的。

1 利用趣味型问题，激发学生自主学习兴趣

案例（1） 学习《圆的定义》时，提出:车轮为什么要做成圆形的?能做成三角形、方形、椭圆形吗?使学生感到自然、必要和富有趣味，而且引起学生积极思考，自己找到答案:圆上各点到圆心的距离都相等，可以使车辆在阻力比较小的情况下平稳地运动。

2 利用开放型问题，培养学生求异思维能力

适当开放题目的条件或结论，为学生提供自主探索与创新的空间，有利于学生活跃思维，展示创新意识和能力。求异思维就是寻求变异、不墨守成规的一种思维活动。在教学过程中，教师要鼓励学生大胆猜想，通过变换思维角度使解题过程更加简洁、解题方法更佳。通过问题解决的不同方法以及设计一些有针对性的变式问题，从多个维度培养学生探索问题的能力，通过问题的解决达到培养学生求异创新思维能力的目的。

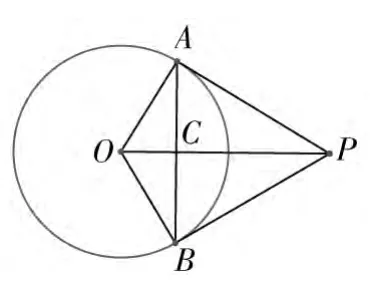
图1

案例（2） 如图1，PA、PB切⊙O于A、B，则可以得到哪些结论?

（PA=PB，OP⊥AB，∠APO=∠BPO，∠AOP=∠BOP ，AC=BC……）

题目只给出条件，学生通过探索不但使问题得到解决，同时拓展了思维，求异思维能力也得到提高。

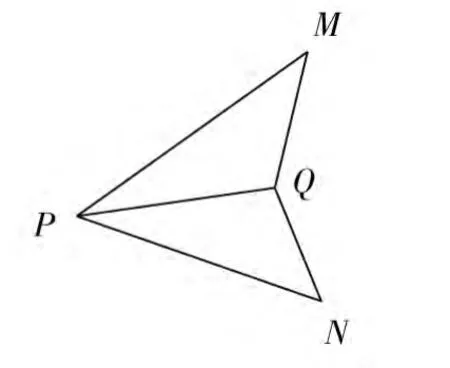
图2

案例（3） 如图2，在△PMQ和△PNQ中，PQ平分∠MPN，为了使这两个三角形全等，你认为应当添加一个什么条件:___________。

学生的解答哪些是成立的?哪些是不成立的?这就要求我们紧扣全等三角形的判定方法，引导学生自主探究，通过辨析起到事半功倍的作用。

3 利用互逆型问题，培养学生逆向思维能力

逆向思维就是对司空见惯的似乎已成定论的事物或观点反过来思考的一种思维方式。在教学过程中，除了对学生进行适当的正向思维训练外，还应当设计一些逆向性问题，让学生学会从问题的不同方向探究解决方法，利用逆向思维与正向思维的相互发展与促进，达到培养学生逆向思维能力的目的。

案例（4） 顺次连结四边形ABCD各边的中点得到的四边形（也称四边形ABCD的中点四边形）是平行四边形。证明上述命题后，可进行如下的变式:

变式一:平行四边形、矩形、菱形、正方形的中点四边形是什么特殊四边形?

变式二:当四边形ABCD必须满足什么条件时，它的中点四边形是平行四边形、菱形、矩形、正方形，从中你能发现什么规律?

其中，变式二就是迫使学生要进行逆向探求，通过上述问题的解决使学生的逆向思维能力得到提高。

4 利用迷惑型问题，培养学生批判思维能力

中学生敢于对书本上的知识或成人的意见提出质疑，是因为他们思考问题时受条条框框的束缚较小，可他们的批判性见解经常是片面的，有时甚至是错误的。教师有必要适时地设计迷惑性较强的问题，让学生展开争论，使他们的批判性思维趋于成熟、准确。

案例（5） 关于x的方程ax2+bx+c=0（a≠0），下列命题正确的是（ ）:

A．若b=0，则两根互为相反数。 B．若a=c，则两根互为倒数。

C．若 ac＞0，则两根同号。 D．若 ac＜0，则两根异号。

对这道题上当受骗的学生很多，教师应及时引导学生进行辩论，帮助学生找出产生错误的原因，使他们的批判性思维趋于全面和正确。

5 利用联想型问题，培养学生联想思维能力

将不同事物联系起来进行思考，是培养创造性思维能力的一种重要方式。在数学思维活动中，比较常见的联想思维有类比联想、数形联想、反向联想和化归联想等。教师在教学设计时，可以根据授课内容设计联想型问题，灵活地运用这些方法。

案例（6） 如果下列方程:x2+（2m－1）x+m2=0，4x2+4mx+（m2+m）=0，x2+（2m－3）x+m2=0至少有一个方程有实根，求m的值。

此题正面解答相当复杂，可引导学生联想它的反面——三个方程都无实根，问题便迎刃而解。

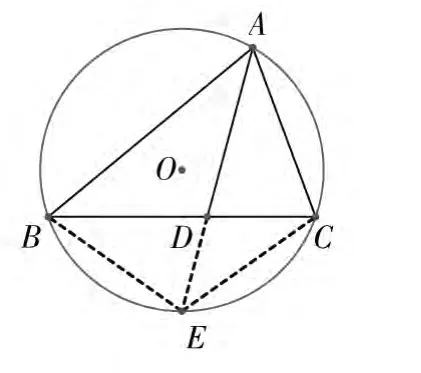
图3

案例（7） 如图3，已知AD为△ABC的角平分线，求证:AB·AC=AD2+DB·DC。

对这道题学生常感不知所措，但当引导学生联想到“相交弦定理”时，问题便迎刃而解。“它山之石，可以攻玉。”设计联想型问题可以让学生开阔思维，考虑问题更全面。

6 利用探索型问题，培养学生探索思维能力

数学问题的解决其核心特征就是探索性。通过设计探索性问题，让学生在探索中发现结论，体验“观察、猜想、抽象、概括、归纳、证实”这一思维过程。

案例（8） 如图4，若P为等腰ΔABC底边BC上的动点，求证:P到两腰的距离之和为定值。

变式一:当P在BC延长线上运动时，P到两腰的距离之和有什么关系?

变式二:当P在等腰ΔABC所在平面上运动时，P到两腰的距离之和有什么关系?

变式三:能否把上述结论推广到任意三角形?

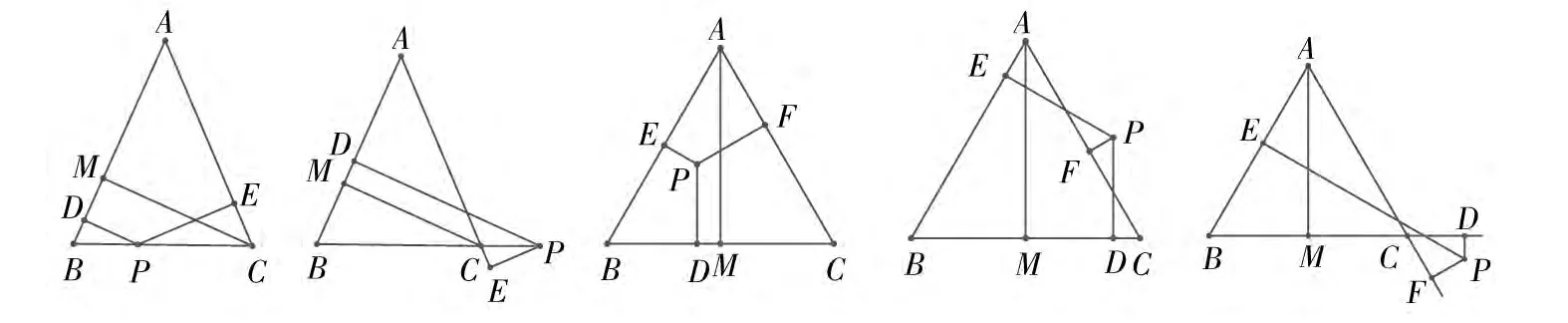
图4

上述问题的解决，需要学生经历观察、猜测、类比和归纳这一“发现”过程，通过问题的解决，使学生形成良好的认知结构，构建数学知识网络。

案例（9） 如图5，在平面上，平行四边形ABCD的顶点A、B、C、D到直线m的距离分别为a，b，c，d。1）求证:a+c=b+d;2）若把直线m向上平行移动，1）中的结论将怎样变化?证明之。

直线m向上平行移动过程中，1）中的结论依然成立。把“运动”思想渗透到数学内容之中，让学生在运动中探究问题的本质。

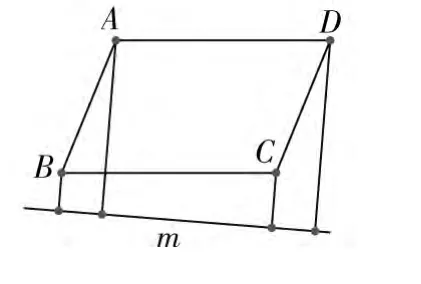
图5

7 利用应用型问题，培养学生应用思维能力

数学是人们生活、劳动和学习必不可少的工具，设计应用型问题，给学生营造一种生动的现实环境和实际需求，让他们利用所学知识解决生活中遇到的数学问题，并自己发现规律和概括数学模型。

案例（10） 把“作△ABC的内切圆”的问题改为:“有一块△ABC木板，今要截出一个最大的圆形材料，应怎样截取?”

对这道题目，学生带着悬念学习，探究意识很浓。设计数学问题，要尽量选择学生熟悉的情境作为背景，让学生了解数学在实际生活中有着广泛的应用，达到强化学生学习动机的目的，在探索实际问题中培养学生的应用意识和创新素质。

案例（11） 把长40米、宽30米的矩形场设计成花园，要求:花坛所占面积为场地面积的一半，整个场地成轴对称和中心对称图形。画出图形，写出方案，列出方程并计算出有关数据。

因所提供的结论与学生所构造的解答之间没有必然唯一确定的联系，学生解答这样的问题不仅需要具有一定的数学推理能力，更需要具有分析问题和解决问题的能力。

8 利用延展型问题，培养学生发散思维能力

延展型问题是指能够进行变化、延伸和拓展的问题。对例习题加以延伸和拓展，不仅能使学生巩固基础知识，而且能提高学生分析问题和解决问题的能力，培养发散创新思维。

案例（12） 如图6，⊙O1与⊙O2的半径分别为R、r，⊙O1与⊙O2外切于点M，过M的直线分别交⊙O1、⊙O2于A、B．你能得到什么结论?

拓展一:如图7，过点M的另一条直线交⊙O1、⊙O2于C、D，你能得到什么结论?

拓展二:如图8，⊙O1与⊙O2内切于点N，上述结论有什么变化?

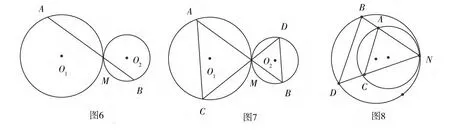
上述问题串有利于激发学生的学习积极性，诱导学生产生解决问题的欲望，通过问题的解决发现它们的一般性规律，对培养学生发散思维能力起到良好的促进作用。设计新颖且具有挑战性的数学问题，有利于培养学生的创新思维能力，教师通过设计恰当的数学问题，能够让学生在解题过程中提高自身的创新思维能力［2］。

［1］李为．初中数学课堂问题设计例谈［J］．中学数学教学参考，2014（8）:19－21．

［2］谢雅礼．论数学开放性问题的教学价值［J］．福建基础教育研究，2011（11）:79－81．

（责任校对 游星雅）

G632

A

1674－5884（2015）07－0017－03

10．13582/j．cnki．1674 － 5884．2015．07．006

20141203

林永晖（1964－），男，福建永春人，中学一级教师，主要从事教育管理研究。