雍龙泉，刘三阳，拓守恒，邓方安，高 凯

（1.西安电子科技大学 数学与统计学院，西安710071；2.陕西理工学院 数学与计算机科学学院，陕西 汉中723001）

线性互补问题（linear complementarity problem，LCP）是一类应用广泛的优化问题，它为线性规划和二次规划提供了统一的研究框架，因此求解线性互补问题的有效算法备受关注［1－2］.对线性互补问题的研究，目前主要集中在理论与算法两方面，前者主要研究其解的存在性、唯一性、稳定性和灵敏度分析，后者主要建立其有效的求解方法和相应的收敛性分析.求解线性互补问题的算法有很多，经典的有Lemke算法；近年来（针对单调线性互补）出现了一些具有多项式复杂性的算法，如投影法、内点法、非光滑牛顿法、光滑牛顿法和迭代法等［3－7］.

绝对值方程（absolute value equation，AVE）等价于一个不可微的NP难优化问题.目前对于绝对值方程的研究主要集中于其解的存在性和唯一性以及建立有效的算法并进行相应的收敛性分析［8－15］.

本文研究线性互补问题与绝对值方程之间的内在关系，给出了二者的等价转化，并进行了证明.本文用I表示单位矩阵，‖·‖表示2范数，⊥表示两个向量正交：即

1 预备知识

定义1 如果对∀z∈ℝn，都有zTMz≥0，则矩阵M∈ℝn×n称为半正定矩阵；如果对∀z∈ℝn，z≠0，都有zTMz＞0，则M称为正定矩阵.这里定义的半正定矩阵与正定矩阵不限制对称性［5，16－17］.

线性互补问题即求向量z∈ℝn，满足Mz＋q≥0，z≥0，zT（Mz＋q）＝0，简记为LCP（M，q）.

当矩阵M是半正定矩阵时，LCP（M，q）称为单调线性互补问题［16］.

引理1［5］设矩阵M∈ℝn×n为一半正定矩阵，对于任意的q∈ℝn，若LCP（M，q）是可行的，则LCP（M，q）必有解，且其解集为凸集.

引理2［5］设矩阵M∈ℝn×n为一正定矩阵，则对于任意的q∈ℝn，LCP（M，q）有唯一解.

上述判定线性互补问题解存在的条件仅是充分条件，而非必要条件［17］.更多关于线性互补问题解存在的条件可参见文献［5］.

引理3［8］绝对值方程

2 线性互补问题到绝对值方程的转化

定理1 线性互补问题Mz＋q≥0，z≥0，zT（Mz＋q）＝0等价于如下绝对值方程：

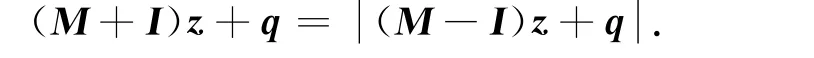
证明：对∀a，b∈ℝ，都有

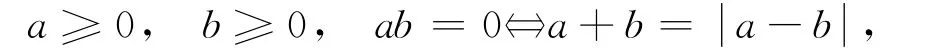
该结论对向量也成立.因此，令a＝Mz＋q，b＝z，则有

即

定理2 若1不是矩阵M的特征值，则LCP（M，q）等价于如下绝对值方程：

这里x＝（M－I）z＋q.

证明：利用定理1可知

由于1不是M 的一个特征值，故（M－I）－1存在.令x＝（M－I）z＋q，即z＝（M－I）－1（x－q），可得

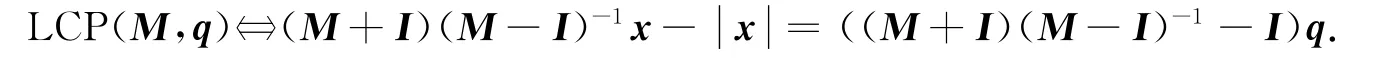
定理3 若1不是矩阵M的特征值，则LCP（M，q）等价于如下绝对值方程：

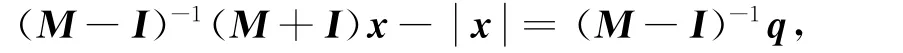
证明：令

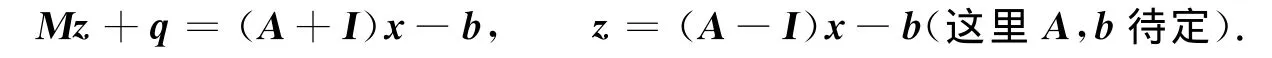
结合引理3，有

下面给出A，b的表达式.

把z＝（A－I）x－b代入Mz＋q＝（A＋I）x－b中，有

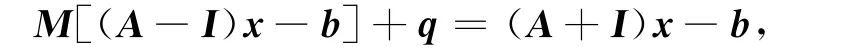
由于1不是M的一个特征值，故（M－I）－1存在.简单计算可得

从而

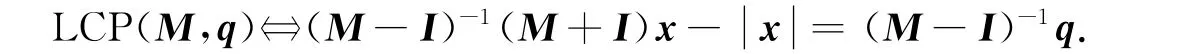
又由z＝（A－I）x－b得

证毕.

当1是矩阵M的特征值时，对线性互补问题中的M和q乘以某个正常数λ，使得1不是矩阵λM的特征值（此时线性互补问题的解不变），再应用定理2或定理3可把线性互补问题转化为绝对值方程.

考虑LCP（M，q），其中：

M的特征值为

对于∀z≠0，由于

因此矩阵M是正定矩阵，易求得该问题的唯一解为z＊＝（2.5，0.5，0，2.5）T.

由于1是矩阵M的特征值，因此定理2和定理3不能直接使用.令λ＝3，则λM 的特征值不为1，且LCP（λM，λq）与LCP（M，q）具有共同的最优解z＊，而LCP（λM，λq）可应用定理2或定理3转化为绝对值方程.

3 绝对值方程到线性互补问题的转化

Prokopyev［21］给出了（在无任何条件下）绝对值方程转化为线性互补问题的一种方法，但该转化增加了问题的维数；胡胜龙等［22］通过重构技巧（在无任何条件下）把绝对值方程转化为线性互补问题，但该方法的实现有一定难度.

定理4（有条件转化）若1不是A的特征值，则AVE等价于LCP（M，q）：

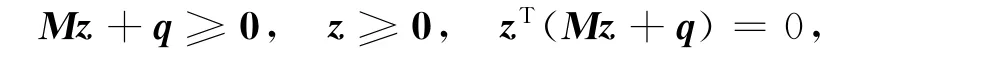
其中：z＝（A－I）x－b；M＝（A＋I）（A－I）－1；q＝（（A＋I）（A－I）－1－I）b.

证明：由于1不是A的一个特征值，故（A－I）－1存在.结合引理3，有

令z＝（A－I）x－b，即x＝（A－I）－1（z＋b），可得

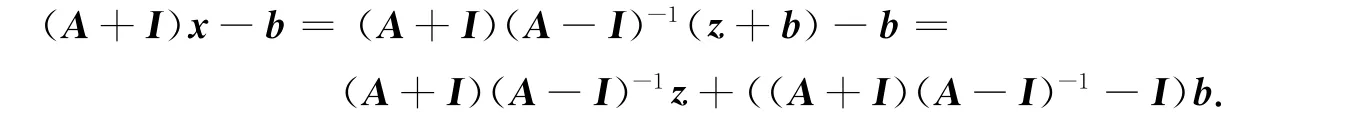
若令

则有

即

其中：z＝（A－I）x－b；M＝（A＋I）（A－I）－1；q＝（（A＋I）（A－I）－1－I）b.

推论1 若矩阵A的奇异值（即矩阵ATA特征值的非负平方根）都大于1，则矩阵M＝（A＋I）（A－I）－1是一个正定矩阵.

证明：若矩阵A的奇异值都大于1，则（A－I）－1存在（否则，∃ξ≠0，使得（A－I）ξ＝0，即Aξ＝ξ，表明1是A的特征值，从而1也是A的奇异值，矛盾），且ATA的所有特征值都大于1，因此，对任意的z≠0都成立zT（ATA－I）z＞0.而

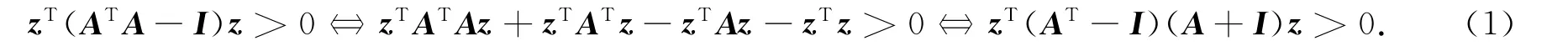
由于（A－I）－1存在，令z＝（A－I）－1v（z≠0，故v≠0），代入式（1）并整理得

即

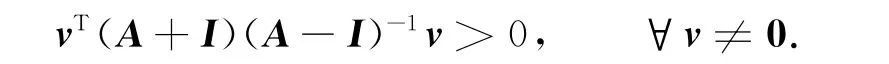
表明矩阵M＝（A＋I）（A－I）－1是一个正定矩阵.

矩阵A的奇异值都大于1⇒矩阵M＝（A＋I）（A－I）－1是一个正定矩阵⇒对应的LCP（M，q）具有唯一解⇒相应的AVE具有唯一解.

综上可见，线性互补与绝对值方程具有密切的内在联系.基于上述对两类问题的转化，在求解任意绝对值方程时，都可以通过求解如下无约束优化问题

获得绝对值方程的解；在求解任意线性互补问题时，都可以通过求解如下无约束优化问题

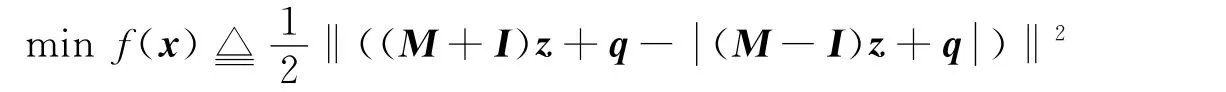
获得线性互补问题的解.该方法对矩阵A或M 可以没有任何限制，当目标函数值收敛到零，则达到最优解；当目标函数值收敛不到零，则原问题可能无解；因此该方法具有较强的实用性.

［1］Billups S C，Murty K G.Complementarity Problems［J］.Journal of Computational and Applied Mathematics，2000，124：303－318.

［2］Cottle R W，PANG Jong－shi，Stone R E.The Linear Complementarity Problems［M］.San Diego：Academic Press，1992.

［3］Kojima M，Megiddo N，Noma T，et al.A Unified Approach to Interior Point Algorithms for Linear Complementary Problems：A Summary［J］.Operations Research Letters，1991，10（5）：247－254.

［4］Murty K G.Linear Complementarity，Linear and Nonlinear Programming［M］.Berlin：Heldermann Verlag，1988.

［5］韩继业，修乃华，戚厚铎.非线性互补理论与算法 ［M］.上海：上海科学技术出版社，2006：31－250.（HAN Jiye，XIU Naihua，QI Houduo.Theory and Algorithm for the Nonlinear Complementarity ［M］.Shanghai：Shanghai Science and Technology Press，2006：31－250.）

［6］YONG Longquan.Interior Point Algorithms for Monotone Linear Complementarity Problem ［J］.ICIC Express Letters，2011，5（3）：775－781.

［7］YONG Longquan.Research on Linear Complementarity Problem and Related Application ［J］.Engineering Technology Press，2010（2）：287－290.

［8］Mangasarian O L，Meyer R R.Absolute Value Equations［J］.Linear Algebra Appl，2006，419（2／3）：359－367.

［9］Rohn J.An Algorithm for Solving the Absolute Value Equation［J］.Electronic Journal of Linear Algebra，2009，18：589－599.

［10］YONG Longquan，LIU Sanyang，ZHANG Shemin，et al.A New Method for Absolute Value Equations Based on Harmony Search Algorithm ［J］.ICIC Express Letters，Part B：Applications，2011，2（6）：1231－1236.

［11］雍龙泉，拓守恒.基于凝聚函数的拟牛顿算法求解绝对值方程 ［J］.系统科学与数学，2012，32（11）：1427－1436.（YONG Longquan，TUO Shouheng.Quasi－Newton Method to Absolute Value Equations Based on Aggregate Function［J］.Journal of Systems Science and Mathematical Sciences，2012，32（11）：1427－1436.）

［12］YONG Longquan.An Iterative Method for Absolute Value Equations Problem ［J］.Information，2013，16（1）：7－12.

［13］雍龙泉，刘三阳，拓守恒，等.具有2n个解的绝对值方程问题 ［J］.吉林大学学报：理学版，2013，51（3）：383－388.（YONG Longquan，LIU Sanyang，TUO Shouheng，et al.Absolute Value Equations with 2n－Solutions［J］.Journal of Jilin University：Science Edition，2013，51（3）：383－388.）

［14］Caccetta L，BIAO Qu，ZHOU Guanglu.A Globally and Quadratically Convergent Method for Absolute Value Equations［J］.Computational Optimization and Applications，2011，48（1）：45－58.

［15］雍龙泉，张社民，张建科，等.绝对值方程研究进展 ［J］.陕西理工学院学报：自然科学版，2012，28（1）：33－38.（YONG Longquan，ZHANG Shemin，ZHANG Jianke，et al.Advance in the Study of Absolute Value Equations［J］.Journal of Shaanxi University of Technology：Natural Science Edition，2012，28（1）：33－38.）

［16］雍龙泉，邓方安，陈涛.单调线性互补问题的一种内点算法 ［J］.数学杂志，2009，29（5）：681－686.（YONG Longquan，DENG Fang’an，CHEN Tao.An Interior Point Method for Solving Monotone Linear Complementarity Problems［J］.Journal of Math，2009，29（5）：681－686.）

［17］雍龙泉，邓方安.线性互补问题中矩阵正定性判别的2点注记 ［J］.吉首大学学报：自然科学版，2009，30（1）：33－35.（YONG Longquan，DENG Fang’an.Two Notes on Positiveness Judgement of Matrix in Linear Complementarity Problem ［J］.Journal of Jishou University：Natural Science Edition，2009，30（1）：33－35.）

［19］魏庆举.绝对值方程的广义牛顿算法及其收敛性 ［D］.北京：北京交通大学，2009.（WEI Qingju.A Generalized Newton Method and Its Convergence for Absolute Value Equations［D］.Beijing：Beijing Jiaotong University，2009.）

［20］雍龙泉.绝对值方程研究综述 ［J］.陕西理工学院学报：自然科学版，2013，29（6）：25－30.（YONG Longquan.Review of Absolute Value Equation［J］.Journal of Shaanxi University of Technology：Natural Science Edition，2013，29（6）：25－30.）

［21］Prokopyev O.On Equivalent Reformulations for Absolute Value Equations［J］.Computational Optimization and Applications，2009，44（3）：363－372.

［22］HU Shenglong，HUANG Zhenghai.A Note on Absolute Value Equations ［J］.Optimization Letters，2010，4（3）：417－424.