●杨 平 胡 芳 杨海兰 (日坛中学 北京 100025)

2014年高考复习中空间几何体的关注点

●杨 平 胡 芳 杨海兰 (日坛中学 北京 100025)

高考中的多面体考什么?《普通高中数学课程标准》指出，几何学是研究现实世界中物体的形状、大小与位置关系的学科.人们通常采用直观感知、操作确认、思辨论证、度量计算等方法认识和探索几何图形及其性质.三维空间是人类生存的现实空间，认识空间图形，并培养和发展学生的空间想像能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力，是高中阶段数学课程的基本要求.影响几何体形状的垂直与平行及其大小的面积与体积、角与距离是必考的内容.

1 影响几何体形状的元素——垂直与平行

在空间点、线、面位置关系问题中，涉及到的垂直与平行元素很多，如线线垂直(有相交线垂直，还有异面直线垂直)、线面垂直、面面垂直;有线线平行、线面平行和面面平行，这些垂直与平行元素又导致几何体的形状特征很特殊，因此，在几何体中研究垂直与平行的价值也就显得更有意义了.

在历年数学高考中，垂直与平行元素是必考的内容之一.

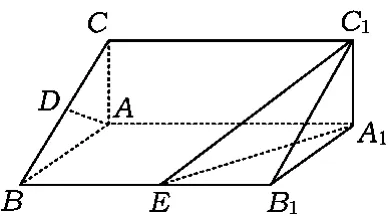
图1

例1如图1，在直棱柱ABC-A1B1C1中，是BC的中点，点 E在棱BB1上运动.证明：AD⊥C1E.

(2013年湖南省数学高考文科试题改编)

解因为 E为动点，所以需证 AD⊥平面CBB1C1.因为 ABC-A1B1C1是直棱柱，所以 BB1⊥平面ABC，且AD⊂平面ABC，得BB1⊥AD.又因为△ABC是等腰直角三角形且D为BC的中点，所以BC⊥AD，从而 AD⊥平面 CBB1C1，又 C1E⊂面CBB1C1，得 AD⊥C1E.

评注此题背景是直三棱柱，直接问题是直线与直线垂直问题，一般通过直线与平面垂直来解决，尤其是异面直线的垂直问题.另外，此题有个隐含条件，即点E在棱BB1上运动，说明C1E是动直线，若要AD与动直线C1E垂直，则AD就需与C1E扫过的平面BCC1B1垂直.

例2如图2，在四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD都是边长为2的等边三角形.证明：PB⊥CD.

(2013年全国数学高考大纲卷文科试题改编)

证明取BC的中点E，联结DE，则ABED为正方形.过点P作PO⊥平面ABCD，垂足为O.

联结OA，OB，OD，OE，因为△PAB 和△PAD 都是等边三角形，知PA=PB=PD，所以OA=OB=OD，即点 O为正方形 ABED对角线的交点，故OE⊥BD，从而PB⊥OE.因为O是BD的中点，E是BC的中点，所以OE∥CD，从而PB⊥CD.

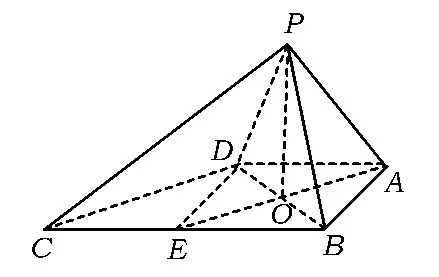
图2

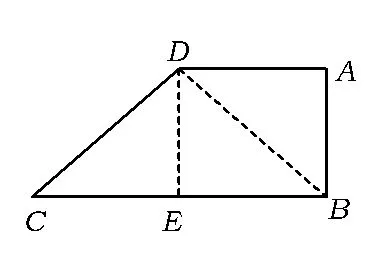
图3

评注这个几何体看似不规则，也没有一条侧棱垂直于底面的特征.我们先研究一下底面(如图3)，这是一个特殊的直角梯形，有垂直、平行的元素，还有正方形、等腰直角三角形等信息;另外，由题意可得，PA=PB=PD，说明点P在平面ABD上的射影落在△ABD的外心，即Rt△ABD的斜边的中点O.

这个四棱锥P-ABCD也可以是由一个正四棱锥P-ABED和一个三棱锥P-CDE组合而成.

例3如图4，在等腰直角三角形ABC中，∠A=90°，BC=6，D，E 分别是 AC，AB 上的点，，O为BC的中点.将△ADE沿DE折起，得到如图5所示的四棱锥A'-BCDE，其中A'O=.证明：A'O⊥平面 BCDE.

(2013年广东省数学高考理科试题改编)

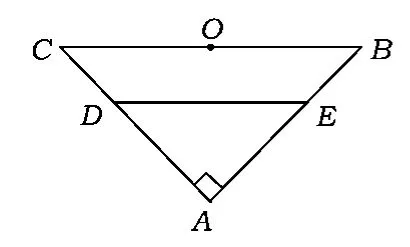
图4

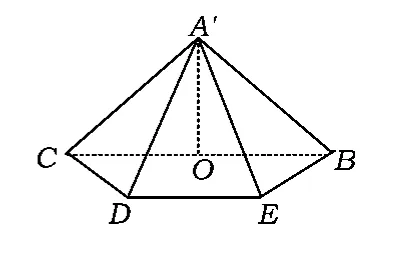
图5

分析这是一个翻折问题，翻折后得到四棱锥A'-BCDE，翻折后的最终结果是侧面 A'CB⊥面BCDE，怎样才能保证平面与平面垂直呢?这里隐含着A'O⊥平面BCDE，也就是点A'在平面BCDE上的射影落在BC的中点O上.

在翻折前后的不变量有：

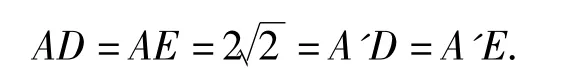
因为O是BC的中点，故等腰直角三角形△ABC中，OE=OD，所以△A'OD≌△A'OE.如图 4，在，由余弦定理可得所以

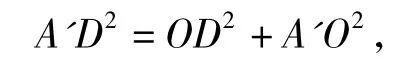
得A'O⊥OD，同理可得 A'O⊥OE，故 A'O⊥平面BCDE.

不难发现，考题中给出的几何体中有三棱锥、四棱锥、三棱柱、四棱柱，有的棱锥有一条侧棱垂直于底面，有的棱锥是正棱锥与其他棱锥的组合体;柱体中有直棱柱，还有斜棱柱;几何体的底面也是形形色色的.这些都只是载体而已，在内涵丰富的几何体中，巧妙地把影响空间几何体形状的垂直和平行元素蕴含其中，既能考查空间想象能力，又能考查推理论证能力.

2 几何体大小的研究对象——面积与体积、角与距离

除了关心几何体的形状外，我们还关心其大小，常见的大小就是面积与体积、角与距离，涉及到的几何体均为柱、锥、台体或其简单的组合体.

2.1 面积与体积

准确记忆体积公式并观察几何体的特征(形状)，进而找到相应的数量关系，是准确求解面积与体积问题的关键.

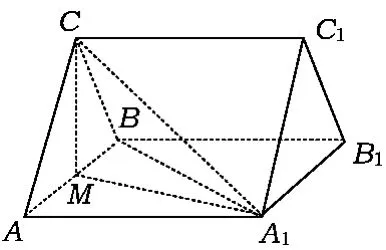
图6

例4如图6，在三棱柱 ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°.

(1)证明：AB⊥A1C;

(2013年数学高考课标卷文科试题)

(1)略.

(2)解取 AB的中点 M，联结 MC，MA1，△ABC与△A1AB都是边长为2的等边三角形，故

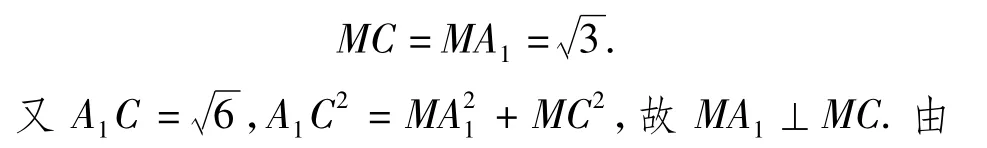
评注此题的背景为斜三棱柱，由于有第(1)小题的铺垫，即垂直的元素很多，故找此三棱柱的高相对容易一些.而三棱锥C-ABA1是一个常见的空间四边形模型，即共底等腰三角形，CA=CB，A1A=A1B，常见的处理方法是取底边AB的中点M，联结 MC，MA1，进而证明 AB⊥平面 MCA1.

2.2 角与距离

由于向量的引入，使得空间的角(线线角、线面角、面面角)，以及距离就显得轻松了.

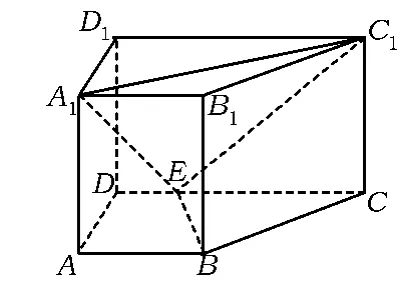
图7

例5如图7，在直四棱柱 ABCD-A1B1C1D1中，AB∥CD，AD⊥AB，AB=2，AD=，AA1=3，E 为 CD 上一点，DE=1，EC=3.求点 B1到平面EA1C1的距离.

(2013年江西省数学高考文科试题改编)

评注这是一个空间点到平面的距离问题，通常的方法为等体积法或向量法，因为此三棱锥恰好在直三棱柱中，且一个面A1B1C1恰位于棱柱的底面，顶点E在另一个底面上，故易求体积，可以考虑用等体积方法;另外，这个几何体为直四棱柱，且，适合建立空间直角坐标系，用向量法求解亦很简单.

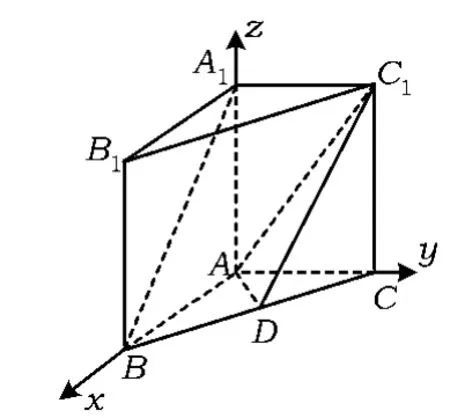
图8

例6如图8，在直三棱柱 A1B1C1-ABC中，AB⊥AC，AB=AC=2，AA1=4，点D是BC的中点.

(1)求异面直线 A1B与C1D所成角的余弦值;

(2)求平面ADC1与平面ABA1所成二面角的正弦值.

(2013年江苏省数学高考试题)

分析此几何体为直三棱柱，且 AB⊥AC，AB=AC=2，AA1=4，适合建立空间直角坐标系，并且图中各点均易得到坐标.

解(1)以A为原点、AB所在直线为x轴、AC所在直线为y轴、AA1所在直线为z轴建立空间直角坐标系，则 A1(0，0，4)，C1(0，2，4)，A(0，0，0)，B(2，0，0)，C(0，2，0)，D(1，1，0)，故

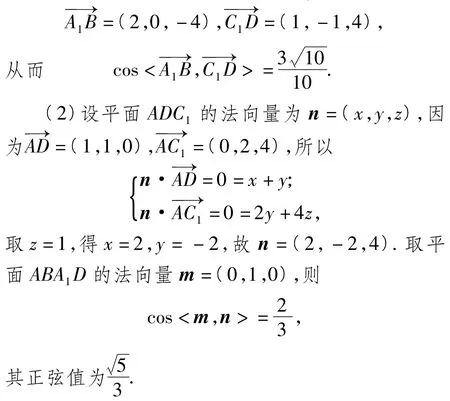
评注向量法是求解立体几何中的角的问题、距离问题的好方法，思路简洁清晰，建立恰当的空间直角坐标系是关键.

3 空间直角坐标系中几何体的点的坐标与法向量

用向量法求解固然简单，但建立空间直角坐标系后，有些运算需要用到的点却不易求出，导致相应的向量求不出，影响了解题，怎么办?其实解决起来很简单，即利用向量相等的定义，找到与所求向量相等且易求的向量坐标，而有些动点的坐标可利用向量共线的充要条件求解.

例 7如图 9，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形，平面 ABC⊥平面AA1C1C，AB=3，BC=5.

(1)求证：AA1⊥平面ABC;

(2)求二面角A1-BC1-B1的余弦值;

(3)证明：在线段BC1上存在点D，使得AD⊥A1B，并求的值.

(2013年北京市数学高考理科试题)

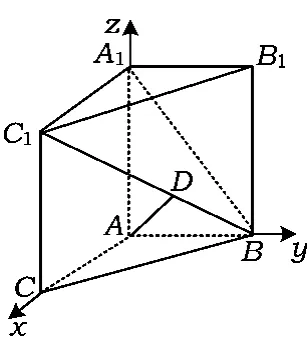
图9

(1)(2)略.

(3)证明以A为原点、AC所在直线为x轴、AB所在直线为y轴、AA1所在直线为z轴建立空间直角坐标系，则B(0，3，0)，C1(4，0，4)，A1(0，0，4).设D(x，y，z)是直线 BC1上的一点，

如何找空间一点的坐标呢?点 A1，C1，B，B1均在坐标平面上，其坐标相对容易找到，而点D不在坐标平面上，就不易找了.注意到一个重要条件：即点D是线段BC1上的动点，由此确定求点D的方案.

方案1求出BC1的方程，进而表示出点D的坐标，但不易实施，因为空间直线方程不好求，需找平面的交线.

方案2利用点D在BC1上，利用三点共线的充要条件，以向量法求解.

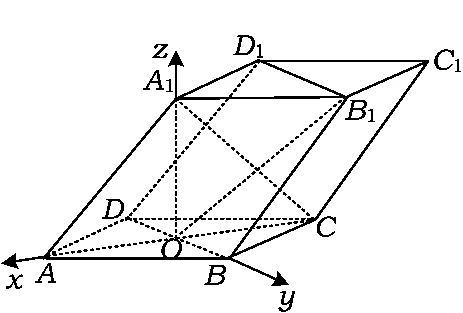
图10

例8如图10，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面

(1)证明：A1C⊥平面BB1D1D;

(2)求平面OCB1与平面BB1D1D的夹角θ的大小.

(2013年陕西省数学高考理科试题)

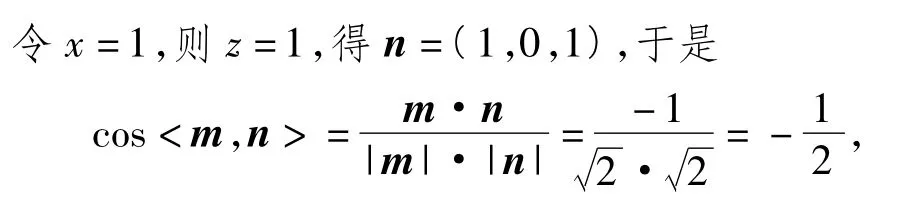
易知平面OCB1与平面BB1D1D的夹角θ为锐角，因此 θ=60°.

评注此几何体中，点 O，A，B，C，D，A1的坐标易求，但点B1的坐标不易求，而在找平面OCB1的法向量时，必须用到点B1的坐标，这个问题是好解决的，因为求法向量时真正用的是向量而不是点B1的坐标，我们发现的坐标易求，同理可得可以用来求.

为了准确快速求解几何体问题，笔者建议：(1)要对形形色色的底面多边形注意研究，如常见的梯形、菱形、等腰三角形，解题时可以将此多边形移出几何体，画出平面图形，找到涉及的平行与垂直元素、数量关系;(2)熟练掌握常见几何体的性质，如正棱锥、直棱柱、正方体、正四面体以及4个面都是直角三角形的四面体;(3)理解概念本质，才能以不变的知识应对百变的试题.