非奇异H-矩阵判定准则
2014-08-25韩贵春高会双肖丽霞
韩贵春,高会双,肖丽霞
(内蒙古民族大学 数学学院,内蒙古 通辽 028000)
非奇异H-矩阵判定准则
韩贵春,高会双,肖丽霞
(内蒙古民族大学 数学学院,内蒙古 通辽 028000)
利用矩阵双对角占优理论给出了含有非零元链、不可约矩阵为非奇异H-矩阵的两个判别方法, 推广了已有的相关结果.
a-双对角占优矩阵;非奇异H-矩阵;不可约矩阵;非零元素链
非奇异H-矩阵是在数值代数、数学物理、经济学、神经网络等领域中具有广泛应用的重要矩阵类, 其判定条件一直是人们研究的热点. 近几年来, 诸学者得到一些新的结论[1-7].本文以文献[1]中关于非奇异H-矩阵判定条件的结论为基础, 给出了含有非零元链、不可约矩阵为非奇异H-矩阵的判别方法.
1 记号与定义
令Cn×n表示n阶复方阵的集合,设A=(aij)∈Cn×n,记:


为行文方便,Ri(A)、Ci(A)(i∈N)分别简记为Ri、Ci(i∈N).
若|aii|≥(>)Ri(∀i∈N), 则称A为(严格)对角占优矩阵, 记为A∈D0(A∈D); 若|aiiajj|≥(>)RiRj(∀(i,j)∈M), 则称A为(严格)双对角占优矩阵,记为A∈DD0(A∈DD);若存在正对角阵X=diag(x1,x2,….xn)使得AX∈D, 则称A为广义严格对角占优矩阵, 记为A∈D*(等价定义为非奇异H-矩阵[2]. 所以非奇异H-矩阵主对角元素aii≠0(i∈N), 本文中总假定所涉及矩阵主对角元素aii≠0(i∈N).
定义1[8]设A=(aij)∈Cn×n, 若存在α∈[0,1], 使:
|aiiajj|≥(>)(RiRj)α(CiCj)1-α,∀(i,j)∈M.
则称A为(严格)α-双对角占优矩阵,记为A∈DD(α0)(A∈DD(α));
引理1[8]设A=(aij)∈Cn×n, 若A∈DD(α),则A为非奇异H-矩阵.
引理2[9]设A=(aij)∈Cn×n, 且A∈DD(α0), 若对于每一满足|aiiajj|=(RiRj)α(CiCj)1-α的 (i,j)∈M都有A的一个非零元素链ai0i1,ai1i2, …,airj0或aj0j1,aj1j2, …,ajtj0,使得i0=i,j0∈J(A) 或i0=j,j0∈J(A), 其中:
J(A)={i||aiiajj|>(RiRj)α(CiCj)1-α,(i,j)∈N}≠∅,
则A为非奇异H-矩阵.
令Γ(A)表示A的有向图;E(A)表示Γ(A)的边集;S(A)表示Γ(A)的回路集合;i∈υ∈S(A)表示i为回路υ的一个顶点.
引理3[10]设A=(aij)∈Cn×n不可约,A∈DD1(α0).若有ei*j*∈E(A)((i*,j*)∈M), 使得|ai*i*aj*j*|>(Ri*Rj*)α(Ci*Cj*)1-α成立,则A为非奇异H-矩阵.
2 有关的主要结论
在本文中,记号同文献[1].下面引入文献[1]中的主要结论:
M1={(i,j)|RiRj<|aiiajj| M2={(i,j)|CiCj<|aiiajj| M3={(i,j)||aiiajj|≥CiCj>RiRj} ; M4={(i,j)||aiiajj|≥RiRj>CiCj}; M5={(i,j)||aiiajj|>RiRj=CiCj} ; M6={(i,j)||aiiajj|≤RiRj,|aiiajj|≤CiCj}. 显然有M=M1∪M2∪M3∪M4∪M5∪M6. 令: 则γij>αij>1,γij>βij>1;zij>xij>1,zij>yij>1. 定理1[1]设A=(aij)∈Cn×n,M6=∅, 如果A满足不等式: 则A为非奇异H-矩阵. 将文献[1]的结果推广到非零元链、不可约矩阵类型中. 定理2 设A=(aij)∈Cn×n,M6=∅, 若对任意的(s,t)∈M1, (i,j)∈M2,A满足不等式: logγstβst≤logzijxij, (1) 且对于满足: logγstβst=logzijxij, (2) 的(s,t)∈M1, (i,j)∈M2都在非零元素链as0s1,as1s2, …,asht0或at0t1,at1t2,…,atks0和ai0i1,ai1i2, …,aipj0或aj0j1,aj1j2,…,ajqi0使得:s0=s,t0∈G(A)或s0=t,t0∈G(A) 和i0=i,j0∈G(A)或i0=j,j0∈G(A), 其中: G(A)={i|logγstβj0j1,st (3) 则A为非奇异H-矩阵. 证明由指标集M1、M2的取法知, 对于任意的(s,t)∈M1, (i,j)∈M2有: 0 0 由式(1)知,必存在常数α∈(0,1),满足: 0 (4) 由式(4)中的logγstβst≤α, 对任意的(s,t)∈M1,γst=αstβst, 有: |assatt|≥(RsRt)α(CsCt)1-α. 由式(4)中的α≤logzijxij, 对任意的(i,j)∈M2,zij=xijyij>1,有: |aiiajj|≥(RiRj)α(CiCj)1-α. 对任意的(k,l)∈M3∪M4∪M5, 及任意的α∈(0,1), 显然有: |akkall|>(RkRl)α(CkCl)1-α. 综上可得,对任意的(i,j)∈M1∪M2∪M3∪M4∪M5=M, 存在α∈(0,1)使得: |aiiajj|≥(RiRj)α(CiCj)1-α. 由式(2)及定理条件可得,对于满足条件: |assatt|=(RsRt)α(CsCt)1-α; |aiiajj|=(RiRj)α(CiCj)1-α, 的(s,t)∈M1, (i,j)∈M2存在非零元素链as0s1,as1s2, …,askt0或at0t1,at1t2,…,atks0和ai0i1,ai1i2, …,aipj0或aj0j1,aj1j2,…,ajqi0使得s0=s,t0∈J(A)或s0=t,t0∈J(A)和i0=i,j0∈J(A)或i0=j,j0∈J(A).而由式(4)可得J(A)≠∅, 故根据引理2知,A为非奇异H-矩阵. 定理3 设A=(aij)∈Cn×n不可约,M6=∅,且对任意的(s,t)∈M1, (i,j)∈M2,A满足不等式: logγstβst≤logzijxij. 若有ei*j*∈E(A)((i*,j*)∈M2)使得: logγstβst (5) 则A为非奇异H-矩阵. 证明类似于定理2的证明可得,对任意的(i,j)∈M1∪M2∪M3∪M4∪M5=M, 存在α∈(0,1)使得: |aiiajj|≥(RiRj)α(CiCj)1-α. 即A∈DD1(α0), 且由条件知A不可约.又由式(5)可得存在某一ei*j*∈E(A)((i*,j*)∈M2⊂M)满足: |ai*i*aj*j*|>(Ri*Rj*)α(Ci*Cj*)1-α. 综上,由引理3可得,A为非奇异H-矩阵. [1]李敏,孙玉祥.α-对角占矩阵的讨论及其应用[J].工程数学学报,2009,26(5):941-945. [2]Bru R,Corral C,Gimenez I,et al.Classes of general H-matrices[J]. Linear Algebra and Applications,2008,429:2358-2366. [3]Yao-tang Li,Yan-yan Li.Some new bounds on eigenvalues of the Hadamard product and Fan product of matrices[J]. Linear Algebra and Appl,2010,432:536-545. [4]GUO Zhijun,YAN Jianguang. A new criteria for a matrix is not generalized strictly diagonally dominant matrix[J]. Applied Mathematical Sciences,2011,5:273-278. [5]Hadjidimos A,Lapidakis M,Tzoumas M.On iterative solution for linear complementarity problem with an H+-matrix [J]. SIAM J MATRIX ANAL APLL,2012,33(1):97-100. [6]李敏,李庆春.非奇异H-矩阵的新判定准则[J].工程数学学报,2012,29(5):715-719. [7]高慧敏,陆全,徐仲,等.非奇异H-矩阵的一组细分迭代判定条件[J].数学杂志,2013,33(2):329-337. [8]黄庭祝.Ostrowski定理的推广与非奇异H-矩阵的条件[J].计算数学,1994,16(1):19-24 [9]李庆春.广义严格对角占优矩阵的判定[J].高等学校计算数学学报,1999(1):87-92. [10]李阳,宋岱山,路永洁.α-双对角占优与非奇异H-矩阵的判定[J].合肥工业大学学报,2005,28(12):1624-1626. 责任编辑:时凌 CriteriaforNonsingularH-Matrices HAN Gui-chun,GAO Hui-shuang,XIAO Li-xiao (School of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028000,China) In this paper, two criteria for nonsingularH-matrices for nonzero elements chains and irreducible matrices are given by using the theory of double diagonally dominant matrices.The known result is generalized. α-double diagonally dominant matrices; nonsingularH-matrices; chain of nonzero elements; irreducible matrices 2013-12-30. 内蒙古民族大学科学研究基金项目(NMD1226). 韩贵春(1978- ), 女,硕士,讲师,主要从事数值代数与矩阵的研究. O151.21 A 1008-8423(2014)01-0068-03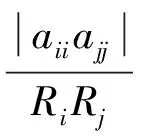
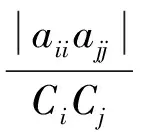
3 定理1的推广
