荣俊杰,尤军峰,文立华,校金友

(1.西北工业大学航天学院, 710072, 西安; 2.中国航天科技集团公司四院四十一所固体火箭发动机燃烧、热结构与内流场国防科技重点实验室, 710025, 西安)

弹性动力学瞬态问题的频域边界元快速解法

荣俊杰1,尤军峰2,文立华1,校金友1

(1.西北工业大学航天学院, 710072, 西安; 2.中国航天科技集团公司四院四十一所固体火箭发动机燃烧、热结构与内流场国防科技重点实验室, 710025, 西安)

为解决常规基于离散傅里叶变换的频域边界元法难以解决无阻尼和低阻尼系统瞬态分析的问题,将指数窗口法与频域边界元法相结合,并采用预校正快速傅里叶变换(pFFT)方法加速边界元求解。为进一步提高分析效率,针对频域边界元法所形成的系列线性方程组,提出了一种最小二乘外推法以获得较高精度的迭代初值,可使初始解残差小于10-2,从而显著减少了迭代次数;将新型的子空间回收算法用于频域系列线性方程组的求解,加快了方程组的迭代收敛速度。算例表明,所提出的方法可显著减少频域边界元法的迭代次数,从而提高了计算效率,并有效降低了迭代解法的内存消耗。

弹性动力学;边界元法;迭代解法;子空间回收

弹性动力学的波动方程是研究固体中机械波传播的理论基础,它的数值求解是力学、材料学、岩土工程学、地震学等众多学科和工程领域的关键问题。边界元方法是一种重要的工程数值方法,它在弹性动力学波动方程的数值求解中也得到了广泛的应用[1]。

弹性动力学问题的边界元分析有3种基本途径[2]:一是时域边界元法,它采用时域基本解,同时在时间域和空间域进行离散求解;二是边界-区域积分方程法,它采用差分法离散时间导数项,再利用弹性静力学基本解获得原问题对应的边界-区域积分方程;三是频域边界元法,它通过拉普拉斯或傅里叶变换将时域问题转化为频域中的椭圆边值问题,采用边界元法来求解,再通过逆变换获得时域解。前2种方法存在时域积分的稳定性问题,目前仍是国际研究的热点。最近,时域卷积求积法被用于时域边界元分析中,可以改善时间积分稳定性问题,但其求解效率仍需进一步研究改进[3]。边界-区域积分方程法需要计算体积分,可以采用对偶互易法、径向积分法等,但计算量远比边界积分的大。

频域边界元法是一种较为简便的动力学边界元分析方法,它将时域问题转化为若干个相互独立的频域问题来求解,编程实现简便,适合于并行计算,并可以同时满足动力学系统频域和时域分析的需要,因此受到研究者的广泛关注[4]。但是,当频域边界元法用于无阻尼或低阻尼系统的分析时,时域响应的误差很大甚至得不到正确的结果,这是由离散傅里叶变换的周期性引起的。文献[5]采用指数窗口法(EWM)有效地解决了上述问题,并采用预校正快速傅里叶变换(pre-corrected FFT,简称pFFT)方法对频域边界元法进行了加速,大大提高了弹性动力学边界元分析的效率。

本文旨在进一步提高频域边界元法求解弹性动力学波动问题的计算效率。在频域边界元法中,对于每个采样频率ωk求解一个线性方程组A(ωk)·x(ωk)=b(ωk),目前这些方程组是采用迭代方法独立求解的。由于频域边界元法形成的系数矩阵A(ω)和右端向量b(ω)都是频率ω的光滑函数,所以解向量x(ω)可以用关于ω的有理函数较好地逼近。据此,在解得xk-1,…,xk-M,xk=x(ωk)之后,可以利用这些结果通过插值获得对xk的迭代初值猜测,以减少求解迭代次数,节省求解时间。GCRO-DR[6]是最近提出的一种求解系列线性方程组的算法,它利用子空间回收的思想重用上个线性方程组的求解信息,因此特别适用于求解系数矩阵光滑变化的序列方程组。本文在文献[5]的基础上,提出了解向量x(ω)的有理插值函数外插方法,并将GCRO-DR算法用于频域边界元线性方程组的求解,算例证明本文方法可以显著减少迭代次数。

1 改进的动力学频域边界元法

设弹性区域为Ω,其边界为Γ。弹性动力学问题的频域边界积分方程为

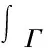
(1)

式中:ω为角频率;cij为自由项;uj和σj分别为边界位移和力;Uij和Tij分别为频域弹性动力学基本解;左边的积分为Cauchy主值积分。设畸变波和膨胀波速度分别为cp和cs,波数为kp和ks。Uij和Tij的表达式以及与积分方程(1)相对应的边界条件可参见文献[2]。

将边界Γ划分为Ne个三角形单元,采用常元离散边界积分方程(1)并考虑边界条件,可得线性方程组

A(ω)x(ω)=b(ω)

(2)

式中:A(ω)为N×N的系数矩阵,N=3Ne;b(ω)为已知的N维列向量;x(ω)为包含未知位移和边界力的待求向量。

为解决上述问题,文献[7]将数字信号处理领域中的指数窗口法(EWM)引入到结构动力学分析中。文献[5]将该方法与频域边界元法相结合,有效地解决了常规频域边界元法存在的上述问题。

(3)

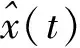
(4)

图1 指数窗口法示意图

设频率和时间分辨率分别为Δω和Δt,则有

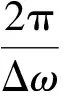
(5)

改进的频域边界元法的基本求解过程如下。

(6)

式中:ωk=kΔω-iη;k=0,1,…,Nω-1。

(2)分别对前(Nω/2+1)个频率ωk(k=0,1,…,Nω/2)求解边界积分方程(1),获得频域响应xew(ωk),并由频域响应的共轭对称性获得后(Nω/2-1)个频率上的响应

式中:xew(k)=xew(kΔω-iη);x*表示x的复共轭。

(7)

(8)

2 线性方程组的加速求解

频域边界元法的主要计算量是对采样频率ωk=kΔω-iη求解系列方程组(2),或写成

Akx=bk,k=0,1,…,Nω/2

(9)

式中:Ak=A(ωk);bk=b(ωk)。本文采用pFFT快速边界元法进行频域求解。下面将首先阐述快速边界元法与方程组迭代解法相结合的思想;然后,为进一步降低求解系列方程组(9)的计算量,提出一种通过最小二乘外推得到迭代初值的方法;最后,采用一种新型系列方程组解法来加速迭代收敛速度。

2.1 迭代解法及pFFT加速方法

当方程组(9)的阶数N较大时,通常采用迭代解法求解(详见2.3节)。迭代解法的核心是计算矩阵-向量积Ax。直接计算Ax的计算量与N2成正比,即计算量为O(N2),不适合大规模计算。近20多年来,人们采用快速边界元法进行Ax的加速计算,取得了巨大成功。快速边界元法按照单元之间的距离,将系数矩阵A分解为近场和远场部分

A=Anear+Afar

(10)

2.2 外推法产生初始解

由式(2)可知,解向量x是频率ω的函数。可进一步假设x是ω的光滑函数。一般地,x关于ω并不是处处光滑的,但多数采样点附近的x仍是光滑的,因此该假设对多数采样频率ωk仍是成立的,这将在第3节通过数值算例予以证明。

由于x是ω的光滑函数,当ω变化不大(即Δω较小)时,临近的若干解xk=x(ωk)几乎是线性相关的。于是,第k个方程组的解xk可以由前面K个解xk-i(i=1,2,…,K)的线性组合来获得,即

(11)

式中:yi为待定系数,可以通过将式(11)代入方程组Akxk=bk,由最小二乘法求得。令X为以前面K个解向量为列的矩阵

并令y=(y1,y2,…,yK)T,则式(11)可写成

xk=Xy

(12)

分别用xk-i(i=1,2,…,K)和矩阵Ak相乘,可得矩阵S=AkX。于是,y是最小二乘问题

的解。采用QR分解方法,令QR=S,则y=R-1Qbk。于是

xk=XR-1Qbk

(13)

实际上,由于Δω不满足足够小的条件,而且x不一定是光滑函数,按式(13)得到的解xk可能存在较大误差,但却可以作为一个较好的迭代初值,即令

(14)

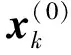
上述产生迭代初值的方法与所采用的迭代解法无关。该方法在电磁场分析领域已有应用,但在边界元动力学分析中还未见采用。已有算例证明,用该方法获得的初始解残差在10-2以下,可以显著减少总迭代次数。

2.3 系列线性方程组的高效解法

由以上基于系列方程组(9)的解向量之间的相关性,通过外推可以获得较好的初始解,从而有效减少迭代次数。实际上,方程组(9)的系数矩阵Ak(k=0,1,…,Nω/2)之间也存在某种相关性(或相似性)。本文采用的GCRO-DR算法[6]是一种基于子空间回收思想的系列线性方程组解法,它利用系列方程组中相邻系数矩阵Ak之间的相似性,每求解一个方程组,就从当前搜索空间中选择一个近似不变子空间作为“回收”子空间,将其继承到下一个方程组的解空间中。回收子空间中包含了与收敛相关的信息,可以加快下一个方程组的迭代收敛速度。

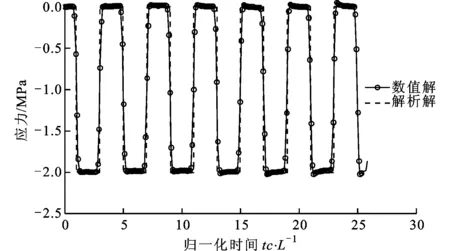
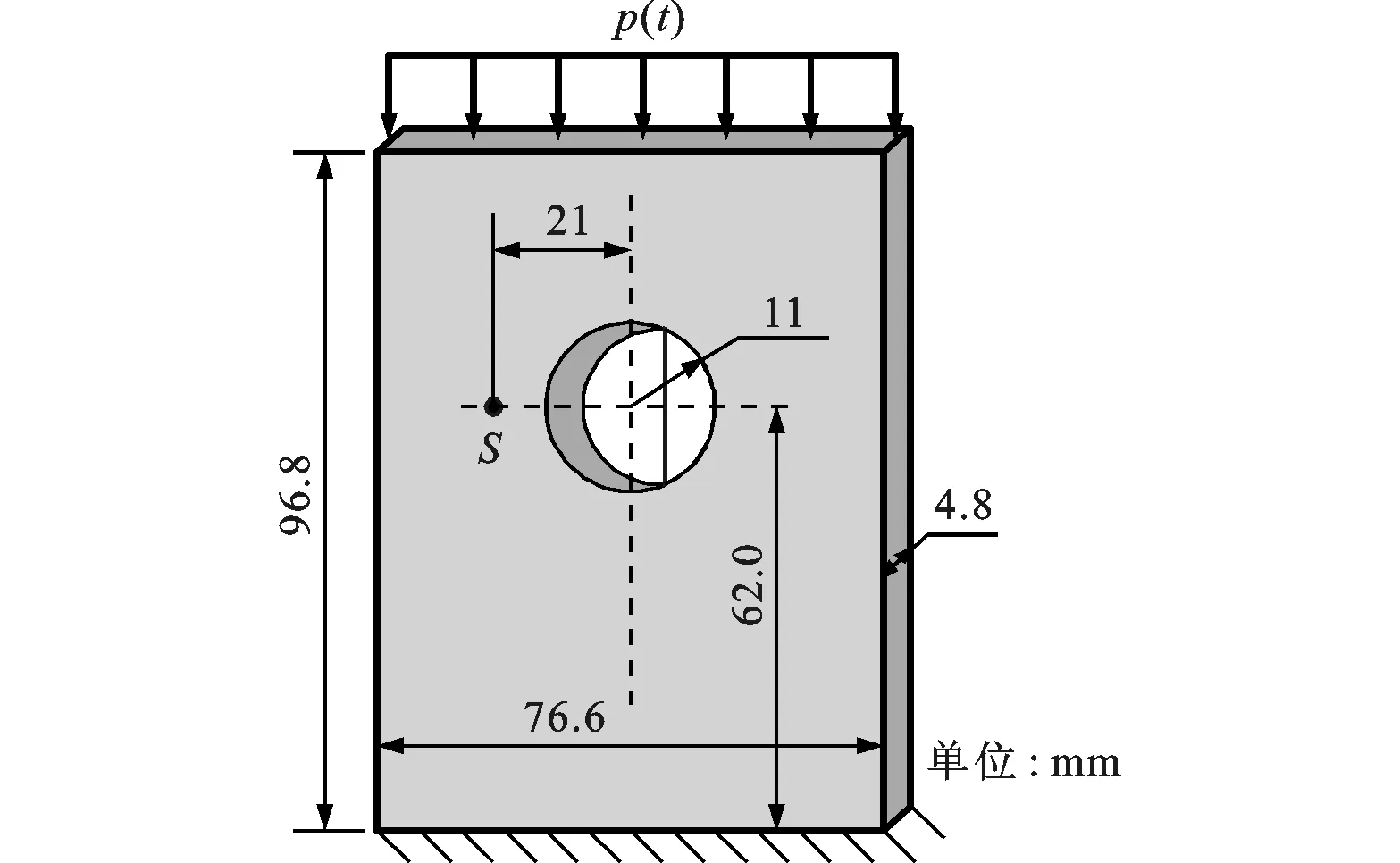
设m为解的搜索空间最大维数。解第k个方程时,GCRO-DR首先在回收空间range(Us)(s

在频域边界元法中,随着频率的增大,解方程组(9)所需的迭代次数也会增加。在GCRO-DR算法中,从第(i-1)个方程继承的回收子空间Us在用于求解第i个方程时,要计算AiUs,导致额外的s次矩阵向量乘法运算,限制了回收子空间的维数s。尤其当频率较小、总迭代次数不大时,AiUs的额外计算量可能抵消子空间回收的优势。如果选择较小的s,则在高频时不能回收足够的信息,会影响子空间回收的效率。为此,本文提出根据总迭代次数来动态调整s的大小,即选取s为当前方程组总迭代次数的β倍。大量数值算例表明,β的取值大致在0.15～0.25之间时,子空间回收的效率较高。s过大会使内存和每步迭代的计算量增大,因此应限定其上限sm。

3 算 例

采用文献[5]中的算例1和算例2来验证本文方法的计算精度和效率。分别采用3种线性方程组迭代解法:①全局GMRES算法[8](使用外推法求初值);②GCRO-DR算法(初值为零向量);③本文算法(采用GCRO-DR算法,用外推法求初值)。

将GCRO-DR算法和本文算法进行对比,可体现外推法的效率。全局GMRES算法是求解单个线性方程组时收敛速度最快的算法,将它与GCRO-DR算法进行比较,可进一步验证子空间回收的优势。所有计算中均使用对角块矩阵对系数矩阵进行预处理。

算例1阶跃载荷下的棱柱

如图2所示,棱柱长度L=3 m,左端固定,用阶跃载荷p(t)加载,p0=-1 MN/m2。令泊松比为0,弹性模量E=211 GPa,密度ρ=7.85Mg/m3。计算中,将柱体表面划分为3 200个单元。采样周期T=0.0155s,采样点数Nω=120,κ=3.0。GCRO-DR算法的参数m=70,sm=20,外推法的参数K=4,收敛误差为1×10-7。

图2 阶跃载荷下的棱柱棒

首先考察本文算法的精度。在设定泊松比为0的条件下,此问题具有解析解[5]。图3给出了固定端应力随时间的变化关系。与解析解对比,本文方法得到的数值解与之基本一致。

t:实验时间; c:波速; L:棱柱长度

为验证本文提出的参数k选取方法的合理性,分别取s=5,25和β=0.2,使用本文算法进行计算,得到迭代次数随频率的变化曲线,如图4所示。当s取5时,在高频范围内迭代次数较多,而当s取20时,在低频范围内迭代次数较多。只有当β=0.2时,在全部频域范围内迭代次数都基本处于最低水平。

图4 本文算法的迭代次数随频率的变化曲线

为验证本文算法的效率,分别用上述3种算法对算例进行计算,表1给出了3种算法的总迭代次数。与全局GMRES算法相比,本文算法的迭代次数有所减少,但减少量有限,这是由于本文算法所使用的GCRO-DR算法在本质上是对重启型GMRES的改进。随着迭代次数的增加,全局GMRES算法的内存消耗及每步迭代的计算量都会增大。表1列出的内存使用情况表明,本文算法的内存消耗小于全局GMRES算法的消耗。与GCRO-DR算法相比,本文算法由于使用了本文提出的外推法计算迭代初值,明显减少了迭代次数。

表1 3种算法计算算例1的总迭代次数和 内存占用量

算法求解所有方程的总迭代次数占用内存/MB全局GMRES算法551524 8GCRO⁃DR算法648717 8本文算法480218 6

算例2冲击载荷作用下的带孔平板

图5 冲击载荷下的带孔平板

通过一个更实际的问题来验证本文算法的精度和效率。图5给出了一铝制平板结构的尺寸、载荷分布以及约束情况。铝板的材料参数分别为:E=69 GPa,ρ=2.7 Mg/m3,ν=0.3。假定冲击载荷均匀施加在平板的顶部,平板的底部固定,如图5所示。试样表面被划分为14 072个三角单元。频域边界元法的参数为:T=0.003,Nω=128,κ=2.0。分别使用上述3种算法进行计算。GCRO-DR算法的参数选择为m=40,sm=20,β=0.25,外推法参数K=4,收敛误差为1×10-4。对于图5中S点的应变,本文算法的计算结果如图6所示,可见除去一些不确定因素外,本文算法所得的结果与试验结果相符。表2给出了3种算法的总迭代次数和内存占用量,从中可以看出,本文算法与其他算法相比迭代次数显著减少,与全局GMRES算法相比,总迭代次数减少了57%,占用内存减少了56%。

图6 S点应变随时间变化图

表2 3种算法计算算例2的总迭代次数和 内存占用量

算法求解所有方程的总迭代次数占用内存/MB全局GMRES算法8122132 4GCRO⁃DR算法659657 4本文算法350861 3

4 结 论

本文将指数窗口法与频域边界元法相结合,有效地解决了常规频域边界元法存在的难以求解无阻尼、低阻尼系统以及求解效率低的问题。频域边界元分析采用pFFT方法进行加速,实现简便,加速效率高。为了进一步提高频域边界元法的计算效率,针对频域边界元法所形成的系列线性方程组,本文提出了一种最小二乘外推法,用于获得较高精度的迭代初值,同时将文献[6]提出的子空间回收算法用于频域系列方程组的快速求解,并给出了其控制参数的取值方法。数值算例表明,本文算法可以显著降低频域边界元分析的迭代次数,并有效降低迭代解法的内存占用量。

[1] 姚振汉, 王海涛.边界元法 [M].北京: 高等教育出版社, 2010: 162-189.

[2] 稽醒, 臧跃龙, 程玉民.边界元法进展及通用程序 [M].上海: 同济大学出版社, 1997: 51-101.

[3] BANJAI L, SAUTER S.Rapid solution of the wave equation in unbounded domains [J].SIAM Journal on Numerical Analysis, 2008, 47(1): 227-249.

[4] CHAILLAT S, BONNET M, SEMBLAT J F.A multi-level fast multipole BEM for 3-D elastodynamics in the frequency domain [J].Computer Methods in Applied Mechanics and Engineering, 2008, 197(49): 4233-4249.

[5] XIAO Jinyou, YE Wenjing, CAI Yaxiong, et al.Precorrected FFT accelerated BEM for large-scale transient elastodynamic analysis using frequency-domain approach [J].International Journal for Numerical Methods in Engineering, 2012, 90(1): 116-134.

[6] PARKS M L, STURLER E, MACKEY G, et al.Recycling Krylov subspaces for sequences of linear systems [J].SIAM Journal on Scientific Computing, 2006, 28(5): 1651-1674.

[7] KAUSEL E, ROESSET J M.Frequency domain analysis of undamped systems [J].Journal of Engineering Mechanics, 1992, 118(4): 721-734.

[8] SAAD Y, MARTIN H S.GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems [J].SIAM Journal on Scientific Computing, 1986, 7(3): 856-869.

[本刊相关文献链接]

李应刚,陈天宁,王小鹏,等.外部动态激励作用下齿轮系统非线性动力学特性.2014,48(1):101-105.[doi:10.7652/xjtuxb201401017]

周生喜,曹军义,Alper ERTURK,等.压电磁耦合振动能量俘获系统的非线性模型研究.2014,48(1):106-111.[doi:10.7652/xjtuxb201401018]

张静,郭宏伟,刘荣强,等.空间含铰可展桁架结构的非线性动力学建模与分析.2013,47(11):113-119.[doi:10.7652/xjtuxb201311020]

刘俊俏,苗福生,李星.二维各向异性功能梯度材料热传导的边界元分析.2013,47(5):77-81.[doi:10.7652/xjtuxb2013 05014]

王焘,校金友,曹衍闯,等.采用Galerkin离散方法的T-小波边界元法.2010,44(12):99-104.[doi:10.7652/xjtuxb2010 12019]

(编辑 葛赵青)

AFastFrequencyDomainBoundaryElementMethodforTransientElastodynamicAnalysis

RONG Junjie1,YOU Junfeng2,WEN Lihua1,XIAO Jinyou1

(1.College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China; 2.National Key Laboratory of Combustion, Flow and Thermo-Structure, The 41st Institute of the Forth Academy of CASC, Xi’an 710025, China)

The conventional frequency-domain boundary element method (BEM) based on discrete Fourier transform is difficult to complete transient analysis of low damped and undamped systems.To solve this problem, the exponential window method is combined with the frequency-domain BEM, and the precorrected fast Fourier transform (pFFT) is used to accelerate the frequency-domain BEM analysis.For solving the sequence of linear systems corresponding to the sampling frequencies with higher efficiency, an extrapolation method is proposed to obtain good initial guesses.In addition, a newly developed Krylov subspace recycling method is employed to solve this sequence of linear systems.Numerical examples demonstrate a dramatic reduction of iterations, which leads to higher efficiency and smaller memory consuming.

elastodynamics; boundary element method; iterative method; Krylov subspace recycling

10.7652/xjtuxb201403021

2013-05-07。

荣俊杰(1990—),男,硕士生;校金友(通信作者),男,副教授。

国家自然科学基金资助项目(11102154, 11074201);教育部高等学校博士学科点专项科研基金资助项目(2010610212009, 2011610211006)。

时间: 2013-12-25

O353.2

:A

:0253-987X(2014)03-0115-06

网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20131225.1701.004.html