王 清

(华北科技学院基础部，北京东燕郊 101601)

0 引言

在非线性偏微分方程的研究中，特别是在孤子理论中，一定会提及KdV方程［1］。它可以通过反散射变换化为线性问题，是完全可积的方程。对于可积方程来说，可以考虑它们的Lax对、贝克隆变换、无穷多守恒律及哈密尔顿结构等［2－8］;可以通过对称分析导出KdV方程族，得出方程族的一些相关性质。对称与守恒律之间存在密切的关系，有了守恒律，可以进一步考虑系统的其它重要性质，例如系统的精确解等。

到目前为止，围绕精确解发展了许多方法，然而非线性偏微分方程的求解仍然非常困难，没有统一而普适的方法，需要继续深入研究。论文主要考虑基于李对称［8－9］的精确解的求解，考虑如下广义的KdV方程

其中u=u(x，t)是未知实函数。方程(1)也可以写成形式Δ=0，其中

注意到，在方程中，令α=0就得到KdV方程。事实上，方程(1)可以通过 Lax 方程［7，10］Lt=［W，L］导出，L和 W 分别满足 Lφ =(－∂2+u+iα∂)φ =λφ 和 φt=Wφ =(－2iαλ +4λ∂ －ux－ iαu+2u∂)φ，其中，α 为常数，λ，φ 分别是特征值和对应的特征函数。

1 方程的对称和优化系统

考虑如下的单参数李群的无穷小变换

相应的群变换的向量场为:

对于方程(1)，延拓向量场写为如下形式:

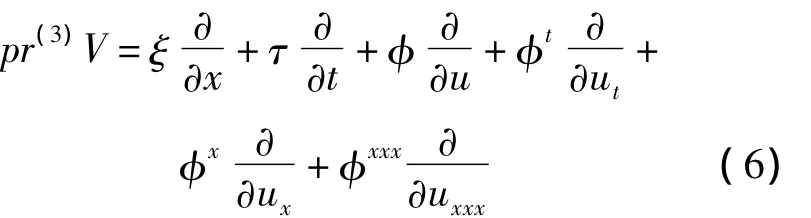
其中 ξ(x，t，u)，τ(x，t，u)，φ(x，t，u)分别用 ξ，τ，φ表示，并且

其中 Dx，Dt为全导数。ξ，τ，φ 满足 pr(3)V(Δ)Δ=0=0，得

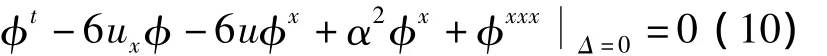
将(7)–(9)代入 (10)，得到决定方程，此决定方程对任意的 x，t，u，ux，uxx，uxxx都成立。因此决定方程中 x，t，u，ux，uxx，uxxx的系数为 0，可求得ξ，τ，φ的表达式，进而得到方程(1)对应的有限维无穷小生成元。

其中 V1，V2，V3，V4在李括号运算是封闭的，列表如下。

表1 李括号

单参变换群 Gi由 Vi(i=1，2，3，4)生成，代入(，，)=exp(εVi)(x，t，u)，结果如下。

向量场的伴随表示［9］为

结合Vi(i=1，2，3，4)的对合关系不难得到关于向量场的伴随表示，如表2所示。

表2 伴随表示

给定非零向量V=a1V1+a2V2+a3V3+a4V4，通过伴随映射在V上的作用尽可能化简a1，a2，a3，a4，利用文献［9］［11］的分析，求得向量场的优化系统为:

2 方程的行波解和级数解

考虑到 Gi(i=1，2，3，4)是对称群，因此若 u=f(x，t)方程(1)的解，则下面的 u(1)，u(2)，u(3)，u(4)也是方程(1)的解。

对时间变换的生成元V1和空间变换的生成元V2，它们的线性组合可以得到偏微分方程的行波解。令 μ =x+kt，则有 u=u(x，t)=f(μ)，可得到下面的常微分方程

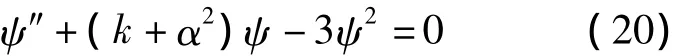
因此只要求得方程(20)中ψ，方程(1)的解u(x，t)通过ψ关于μ求导即可得到。而对于ψ的求解，可采用简单函数［12］的方法求解，由平衡方程可令

当c＞0和d＜0时，

当c＜0和d＞0时，

其中C为积分常数。

对变量变换的生成元V3，有如下的相似变换

和群不变解 w=f(ζ)，即

将上式代入方程(1)，即可将方程(1)约化为如下的常微分方程

对变量变换的生成元V4，有下面的相似变换

和群不变解 w=f(η)，即

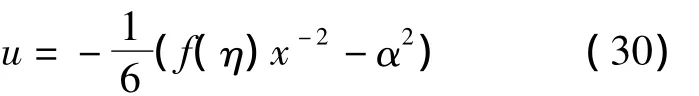
将(30)代入方程(1)，即可将方程(1)约化为如下的常微分方程

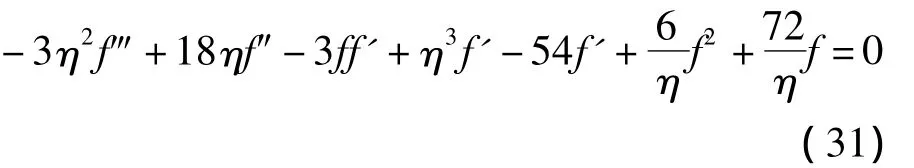
另一方面，又有如下的相似变换

和群不变解 w=f(ρ)，即

将(33)代入方程(1)，即可将方程(1)约化为下面的常微分方程

于是方程(1)的级数解写为如下形式

其中 c0，c1，c2是任意常数，cn(n≥3)由式(36)和式(37)决定。

3 结论

文中将经典李群法应用到广义的KdV方程，得到其对称群，构造了此方程的优化系统，将其转化为低阶的常微分方程，结合简单函数等方法得到了行波解和幂级数解，扩展了李对称理论。李对称理论不仅在解析解方面应用广泛，而且在数值算法方面也在发展，有待进一步研究。

［1］ C.S.Gardner， J.M.Greene， M.D.Kruskal， R.M.Miura.Method for solving the Korteweg－de Vries equation.Physical Review Letters，1967，19:1095－1097.

［2］ 谷超豪，曹策问，李翊神，等.孤立子理论与应用［M］.杭州:浙江科学技术出版社，1990.

［3］ R.Hirota，J.Satsuma.A variety of nonlinear network equations generated from the Backlund transformation for the Tota lattice.Progress of Theoretical Physics，1976，59:64－100.

［4］ E.Misirli，Y.Gurefe.Exact solutions of the Drinfel＇d－Sokolov－Wilson equation using the Exp－function method.Applied Mathematics and Computation，2010，216:2623－2627.

［5］ Geng Xianguo，Wu Lihua.Darboux Transformation and Explicit Solutions for Drinfel＇d－Sokolov－Wilson equation.Communications in Theoretical Physics，2010，6:1090－1096.

［6］ M.Craddock.Fundamental solutions，transition densities and the integration of Lie symmetries［J］.Journal of Differential Equations，2009，246(6):2538－2560.

［7］ Gu Zhuquan.The Neumann system for the 3rd－order eigenvalue problems related to the Boussinesq equation［J］.IL NUOVO CIMENTO，2002，117(6):615－632.

［8］ Peter，J.Olver.Application of Lie Groups to Differential Equations.New York:Springer－Verlag，1986.

［9］ Liu Hanze，Li Jibin，Zhang Quanxin.Lie symmetry analysis and exact explicit solutions for general Burgers equation.Journal of Computational and Applied Mathematics，2009，228(1):1－9.

［10］ 孙海珍，刘亚峰.与广义KdV方程族相关的谱问题及其完全可积性.石家庄铁道大学学报(自然科学版).2013，26(1):106－110.

［11］ Dong Zhouzhou，Chen Yong，Kong Dexing，Wang Zenggui.symmetry reduction and exact solutions of a Hyperbolic Monge－ Ampere Equation.Chinese Annals of Mathematics，Series B，2012，33B(2):309－316.

［12］ 和玲超，庞晶，赵忠龙.应用Bernoulli型简单方程求(2+1)维KP方程的精确行波解.湖南师范大学自然科学学报，2014，37(4):82 －86.