＊

1. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China

2. Departamento de Engenharia Mecânica, UNESP, Ilha Solteira 03001-000, Brizal

An Investigation into the Isolation Performance of Mono-and Bi-stable Systems

Zeqi Lu1, Tiejun Yang1＊, Michael J. Brennan2, Xinhui Li1and Zhigang Liu1

1. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China

2. Departamento de Engenharia Mecânica, UNESP, Ilha Solteira 03001-000, Brizal

Motivated by the need for improving the isolation performance, many research studies have been performed on isolators with nonlinear characteristics. Based on the shape of their phase portrait, such devices can be configured as either a mono- or bi-stable isolator. This paper focuses on investigating the relative performance of these two classes under the same excitations. Force transmissibility is used to measure the isolation performance, which is defined in terms of the RMS of the ratio of the transmitted force to the excitation force. When the system is subjected to harmonic excitation, it is found that the maximum reduction of the force transmissibility in the isolation range using Quasi-Zero stiffness is achieved. When the system is subjected to random excitation, it has the same effect of Quasi-Zero stiffness. Further, optimum damping can be changed with stiffness and has minimum value.

nonlinear isolation; bi-stable system; force transmissibility; random excitation; mono-and bi-stable systems; Quasi-Zero stiffness

1 Introduction

Linear vibration isolators are useful if their natural frequencies are less than 1/2 × excitation frequency (Rivin, 2003; Mead, 1998; Piersol and Paez, 2009). But to achieve low natural frequency vibration isolation, a large static deflection is undesirable. To overcome this problem, a nonlinear isolator can be used which has a large static but low dynamic stiffness (Carrellaet al., 2007, 2009; Le and Ahh, 2011; Shawet al., 2013; Lu and Bai, 2011). Such systems can be modeled by a combination of springs which are arranged geometrically to achieve a low dynamic stiffness and hence a low natural frequency, but at the same time have a low static deflection (Carrellaet al., 2012; Alabuzhevet al., 1989; Robertsonet al., 2009). The review paper (Ibrahim, 2008) compares many nonlinear isolators and shows that research into nonlinear isolators is very active (Tang and Brennan, 2013; Xiaoet al., 2013). Yanget al., (2014) studied the steady-state performance of atwo-stage vibration isolator, which is configured by a bistable oscillator and a linear oscillator, it is found that the single periodic valley and intral-well responses for isolation purposes can be increased by greater bistable stage damping. The paper (Luet al., 2013) incorporates geometric stiffness nonlinearity into a two-stage isolator to overcome the problems of high static deflection and low roll-off rates at high frequency. It has been found that nonlinearity in the lower stage has a profound effect, and significantly improves the effectiveness of the isolation system. So the force transmissibility in the isolation range is reduced as horizontal stiffness increases. However, determining if the isolation performance of the nonlinear isolation system with linear negative stiffness is improved is difficult.

The aim of this paper is to explore the advantages of using linear negative stiffness that can be gained by incorporating geometrical stiffness nonlinearity. After the isolation performance of the system subjected to harmonic excitation is investigated, the force transmissibility under random excitation is determined to show whether the benefit of linear negative stiffness incorporating geometrical stiffness nonlinearity in this case can be achieved.

The positioning of the auxiliary springs with a larger value so that the system becomes bi-stable in the single stage isolator is considered. Although the force transmissibility is defined as in the Luet al. (2013), the RMS of the ratio of the transmitted force to the excitation force is used, as the authors’ intention is to investigate the basic dynamics of the system when it has a response at harmonic excitation and random excitation. Numerical simulation is a simple and appropriate method for this type of analysis.

2 Description of the bi-stable isolation system

Fig. 1 shows a simple lumped parameter model of a nonlinear vibration isolator with linear negative stiffness. The system is the nonlinear isolator which is a particular configuration of three linear springs because of the geometrical configuration (Carrelaet al., 2009). The horizontal springs have critical valueck. If the horizontal stiffness of the system is smaller than the critical value, it is a mono-stable system; otherwise, it becomes bi-stable,which has more complicated dynamic behaviors compared with the mono-stable system (Pellegriniet al., 2012; Mann and Owens, 2013).

The force-deflection curve for the isolator is given by:

which can be written in non-dimensional form as:

Fig. 1 Model of a non-linear isolator that can behave as amono- or double-well system

By choosing appropriate values for the two parametersand ˆlfor the oblique springs, zero dynamic stiffness can be achieved, i.e. Quasi-Zero stiffness can be realized when the critical stiffnessneeds to satisfy:

As shown in Fig. 2, it is found that the phase trajectory presents a single or double well shape whenis smaller or larger thanrespectively. Whenis less than 1, the effect of the horizontal springs is to soften the isolator so that its stiffness is less than the vertical springvk. Whenis larger than 1, it has a detrimental effect that the linear stiffness is increased and the amplitude-frequency curve bends to the right. When the stiffness and initial length of the horizontal spring are fixed, it is found that the bi-stable configuration has a shorter installation length than the mono-stable configuration.

For 0.2xl≤ Eq. (1) can be approximated byin whichand the equation of the motion of the system in Fig. 1 under both harmonic excitationFecos(ωt) and random excitation(Dis the noise intensity) can be approximated by the Duffing equation, which can be written in non-dimensional form as:

Fig. 2 Kinds of phase portraits in a parameter space

It should be noted thatαis the non-dimensional natural frequency of the system when the amplitude of the oscillation is small enough so that the nonlinear termγxˆ3has a negligible effect.

Written as a stochastic differential equation, Eq. (4) becomes:

This equation can be written as the system of integral equations:

Eq. (6) written as the Euler-Maruyama scheme (Kloeden and Platen, 1995; Vanden-Eijnden and Ciccotti, 2006) is given by:

The force transmissibilityFTof the system is the measure used in the investigation. It is defined in terms of the RMS of the ratio of the transmitted forcetfto the excitation forceef.

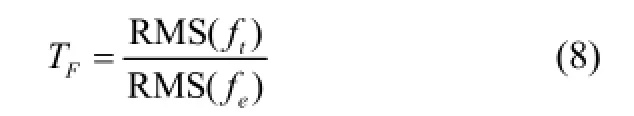
where,ft= 2ζxˆ′+αxˆ+γxˆ3.

3 Harmonic excitation

This section investigates the response behavior of the bi-stable isolation system only subjected to the harmonic excitation which hasfe=cos(Ωτ)and the force transmissibility to the base.

The maximum amplitude of the excitation force that can be applied to the peak in the transmissibility to occur at frequencies lower than non-dimensional frequencyΩ=1 is given by (Carrellaet al(2012)).

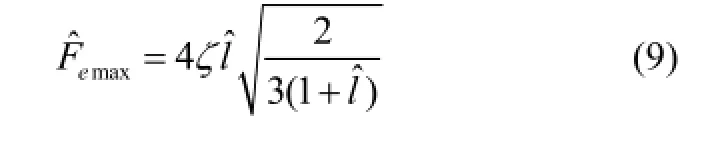
3.1 Frequency response

Fig. 3 The displacement amplitude-frequency responses of the bi-stable isolator at different excitation amplitudes, with increasing frequency; ζ= 0.05,=0.088

Reduction of the force transmissibility using a bi-stable system is of considerable interest in vibration isolation. To provide insight into the isolation performance, numericalsimulations were performed on Eq. (4) for linearly increasing excitation frequencies. The graphs of 3(a-f) show an array of frequency responses that were predicted for different excitation levels. Blue shadow, black points and red line reprent the continuous sampling of the displacement, amplitude of the displacement and equilibrium points of the system respectively. More specifically, when the excitation amplitudeis very small, the response is almost the linear one and the peak is near the linear natural frequency as shown in Fig 3(a). Asis increased, the jump-up phenomenon occurs as the system develops a softening nonlinearity, as shown in Fig. 3(b) and 3(c). Here, the system is constrained to vibrate in one of the wells. Whenhas a moderate level it reveals chaotic motion, reducing the peak resonance and jumping between the two wells around the linear natural frequency, as shown in Fig. 3(d). Fig. 3e and 3f show the dynamic behavior whenhas a large level. It is clear that the system develops the hardening nonlinearity which has a jump-down phenomenon, and the range of the jumping between the two wells extends to lower frequencies. At the highest excitation, the harmonic response is so low at high frequency that the system is constrained to vibrate in one of the wells. There it is seen to have a jump-up phenomenon as shown in Fig. 3(f). The system being constrained to vibrate in which specific well depends on the state of the previous moment. As shown in Fig. 3(d,e,f), the system begins to randomly jump between the two wells around the non-dimensional frequency 1Ω= , so at the next higher excitation frequency, the system is randomly constrained to vibrate in one of the wells.

3.2 Force transmissibility

Fig. 4 shows the force transmissibility of the bi-stable system changing with excitation amplitudefor the cases. And the parameters are the same as those in Fig.3, black points:red points:green points:lue points: It is found thatthe peak of the force transmissibility is reduced and bends to the left with the increasing excitation amplitude; Another observation is that all the curves gather together into one line at low and high frequencies.

Fig. 5 shows the comparison of the force transmissibility between the mono-and the bi-stableconfigurations, with parameters used in Fig. 4, and critical stiffness= 1.17. Red line:= 0, blue line:ˆ= 0.7,black line:, brown line:kˆ= 1.6, green line:ˆ= 2. As shown in Fig. 5(a) with the small excitation amplitude, it is clear that the isolation range is extended to lower frequencies asincreases in the range of the mono-stable system until ˆ 1.17= , then narrows in the range of the bi-stable system. As a bi-stable system, a softening nonlinearity is observed and the peak moves to the right. As shown in Fig. 5(b) with the large excitation amplitude, which may vibrate between the two wells, the same effect of the stiffness ratioon the force transmissibility of the mono- and bi-stable systems at high frequency is indicated.

Fig. 4 The magnitude of force transmissibility of the bi-stable isolator at different excitation amplitudes

Fig. 5 The force transmissibility of the isolator at different ˆk

4 Random excitation

The response and force transmissibility of the bi-stable system subjected to the random excitationwith the parametervarying from 0 to 4, are investigated in this section. The same isolation performance between the harmonic and the random excitation is found for the linear system, but not for the bi-stable system. The degenerative equation of motion of the bi-stable system only subjected to random excitation in Fig. 1 can be approximated by:

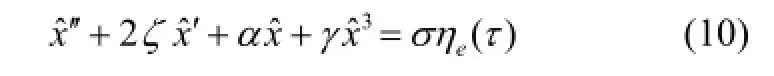
4.1 Time response

When the system is excited by a force which has Gaussian random characteristics, the responses of the mass and the phase portrait are shown in Fig. 6. It can be seen that for lower excitation forces, the system is constrained to vibrate in one of the wells (see Fig. 6(a)). For moderate force levels, the system will jump between the two wells and the displacement response shows some regularity (see Fig. 6(b)). For large force levels, the regular motion is disrupted and the response becomes stochastic again (see Fig. 6(c)).

4.2 Force transmissibility

The definition of force transmissibility for the bi-stable isolation system subjected to random excitation is the same as the previous section, but the noise intensity domain is used. Fig. 7(a) shows the effect of changingon the magnitude of force transmissibility. And the parameters are the same as in Fig. 6. Red line:, black line:green line1.5, light green line:kˆ= 1.8, blue line:kˆ= 2.Whenis fixed at a chosen value, it is found that the force transmissibility of the bi-stable isolation system is decreased asis increased, until, then increased. The optimum force transmissibility at eachis shown as the brown dashed line. Interestingly, both the optimum intensity of noiseand the suppression bandwidth of the valley are increased asincreases. Fig. 7(b) shows the force transmissibility compared with that of the mono-stable isolation system configured by. When the noise intensityis fixed at 0.01, it is found that the minimum magnitude of force transmissibility occurs at the Quasi-zero stiffness. Fig. 7c shows the escaping area in theplane. Shadow area in theplane indicates the escaping area, red crossed points are the same with the brown dashed line in Fig. 7(a) and indicates the optimum points for isolation. It is clear that the optimum noise intensityfor isolation is in very good agreement with the upDˆ-limitation boundary for escaping.

A parametric study was carried out to illustrate how the parameters affect the dynamic behaviour and the results are shown in Fig. 8. Fig. 8(a) shows the effects ofζandon the magnitude of the force transmissibility. It is found that an oblique bowl occurs. Fig. 8(b) shows the optimum dampingζoptvariation withFor the linear isolator, the optimum dampingζoptis the constant which hasζopt= 0.5. For the bi-stable isolator, it is clear that the optimum damping is decreased asincreases, untilthen it increases, as shown in Fig. 8(b). Fig. 9(a) shows the effects ofandon the magnitude of the force transmissibility. It is found that an arc-trench occurs in the3D surfance chart. Fig. 9(b) shows the optimum stiffness ratiochanging withRed cross points reprent numerical results, blue solid line reprents theory reslut predicted by Eq. (2), they are in very good agreement.

Fig. 6 Responses of the system when it is subjected to random excitation, atˆ 0.7= ,ˆ 2= , 0.5ζ=

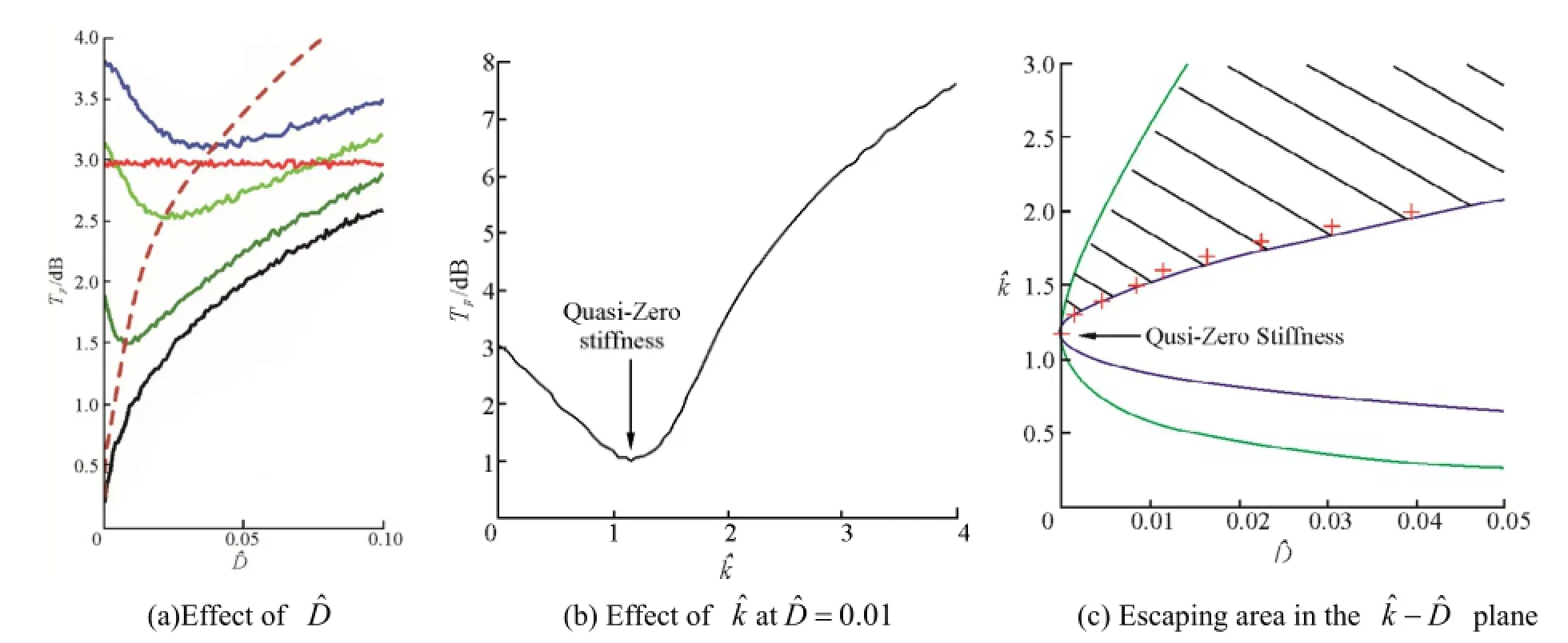
Fig. 7 The magnitude of force transmissibility at differentand

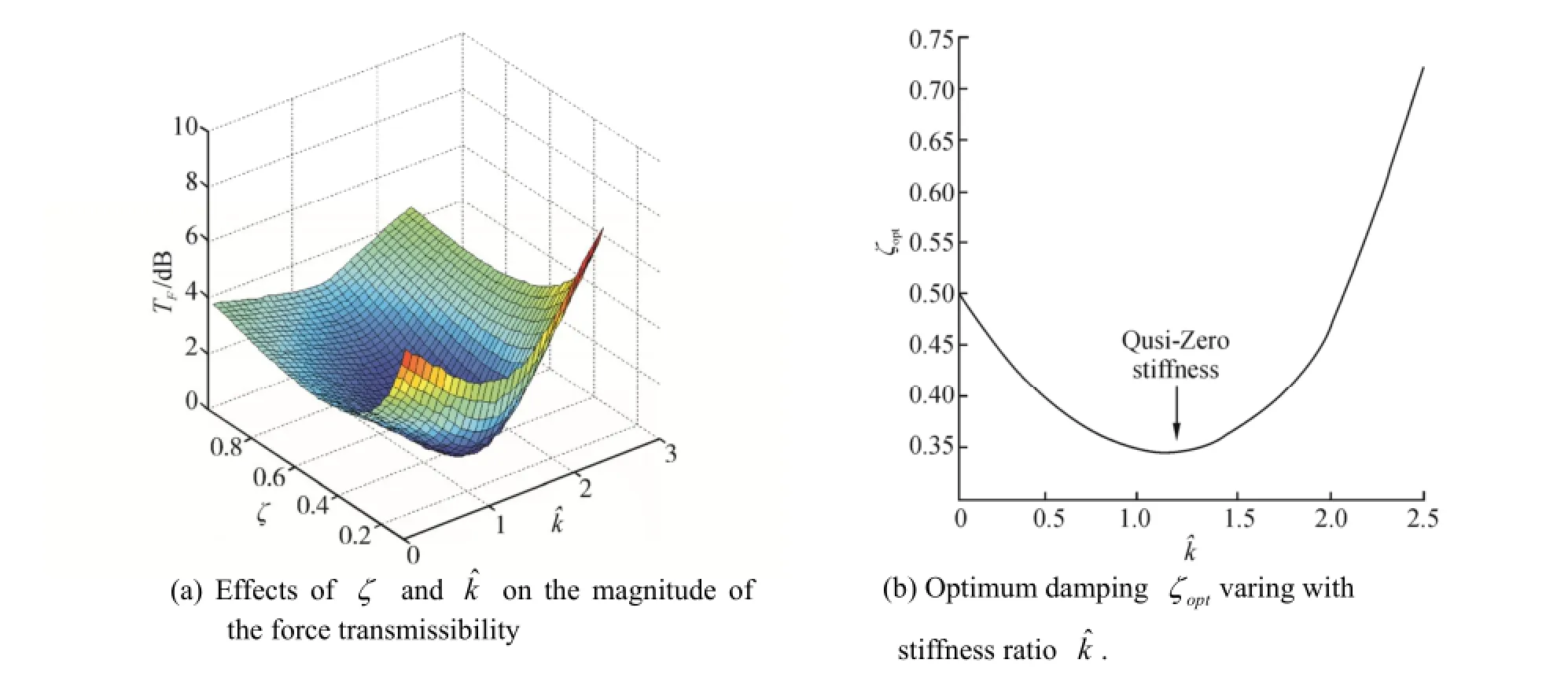
Fig. 8 The magnitude of force transmissibility at differentandζat0.7= ,0.01= .

5 Conclusions

This paper investigates the usage of a nonlinear system with linear negative stiffness to improve isolation performance with the additional benefit of a small installation length as compared with the linear positive stiffness. Force transmissibility is used to measure the isolation performance, which is defined in terms of the RMS of the transmitted force. It is found that the Quasi-Zero stiffness is the optimum stiffness for both isolation of harmonic and random excitation. Three phenomena regarding the nonlinear isolator with linear negative stiffness subjected to random excitation are particularly interesting. First the magnitude of the force transmissibility is decreased asincreases, untilthen it is increased. Second, the optimum damping is changed withand has minimum value. Third, the optimum magnitude of force transmissibility occurs along the arc-trench in theplane.

Alabuzhev P, Gritchin A, Kim L, Migirenko G, Chon V, Stepanov P (1989).Vibration protecting and measuring systems with quasi-zero stiffness. Hemisphere Publishing, New York.

Carrella A, Brennan MJ, Waters TP (2007). Static analysis of a passive vibration isolator with quasi-zero stiffness characteristic.Journal of Sound and Vibration, 301(3-5), 678-689.

Carrella A, Brennan MJ, Kovacic I, Waters TP (2009). On the force transmissibility of a vibration isolator with quasi-zero-stiffness.Journal of Sound and Vibration, 322(4-5), 707-717.

Carrella A, Brennan MJ, Waters TP, Lopes Jr. V (2012). Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness.International Journal of Mechanical Sciences, 55(1), 22-29.

Ibrahim RA (2008). Recent advances in nonlinear passive vibration isolators.Journal of Sound and Vibration, 314(3-5), 371-452.

Kloeden PE, Platen E (1992).numerical solutions of stochastic differential equations. Springer, Berlin.

Le TD, Ahh KK (2011). A viration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat.Journal of Sound and Vibration, 330(26), 6311-6335.

Lu C, Bai H (2011). A new type nonlinear ultra-low frequency passive vibration isolation system.Journal of Vibration and Shock, 30(1), 234-236.

Lu Z, Brennan MJ, Yang T, Li X, Liu Z (2013). An investigation of a two-stage nonlinear vibration isolation system.Journal of Sound and Vibration, 322(4-5), 1456-1464.

Mann BP, Owens BA (2013). Investigations of a nonlinear energy harvester with a bistable potential well.Journal of Sound and Vibration, 329(9), 1215-1226.

Mead DJ (1998).Passive vibration control. Wiley, NY.

Pellegrini SP, Tolou N, Schenk M, Herder JL (2012). Bistable vibration energy harvesrers: A review.Journal of Intelligent Material Systems and Structures, 24(11), 1303-1312.

Piersol AG, Paez TL (2009).Harris′ Shock and vibration handbook 6th edition. McGraw-Hill, New York.

Rivin EI (2003).Passive vibration isolation. American Society of Mechanical Engineers Press, New York.

Robertson WS, Kidner MRF, Cazzolato BS, Zander AC (2009). Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation.Journal of Sound and Vibration, 326(1), 88-103.

Shaw A, Neild S, Wagg D, Weaver P, Carrella A (2013). A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation.Journal of Sound and Vibration, 332(24), 6265-6275.

Tang B, Brennan MJ (2013). A comparison of two nonlinear damping mechanisms in a vibration isolator.Journal of Sound and Vibration, 332(2), 510-520.

Vanden-Eijnden E, Ciccotti G (2006). Second-order integrators for Langevin equations with holonomic constraints.Chemical Physics Letters, 429, 310-316.

Xiao Z, Jing X, Cheng L (2013). The transmissibility of vibration isolators with cubic nonlinear damping under both force and base excitations.Journal of Sound and Vibration, 332(5), 1335-1354.

Yang K, Harne RL, Wang KW, Huang H (2014). Investigation of a bistable dual-stage vibration isolator under harmonic excitation.Smart Materials and Structures, 23(4), 045033.

Author biographies

Zeqi Luwas born in 1985. He is a PhD candidate at Harbin Engineering University. He has presented one paper at an international conference and has one paper published in the Journal of Sound and Vibration. His current research interest is improved passive vibration isolation using nonlinear mechanisms.

Tiejun Yangwas born in Hunan, China in 1972. He received a BSc, MSc in Diesel Engineering and a PhD in Marine Engineering from Harbin Engineering University in 1994, 1997 and 2001, respectively, and then became a postdoctoral researcher at the National Key Laboratory of Rotorcraft and Aeromechanics, Nanjing University of Aeronautics and Astronautics. From 2006 through 2007, he worked at the Dynamic Group of the Institute of Sound and Vibration Research at Southampton University in UK. Now he is a professor at the Power and Energy Engineering College, Harbin Engineering University. He is a member of the Acoustic Society of America, International Institute of Acoustics and Vibration, American Society of Mechanical Engineers. He has published over 70 journal and conference papers regarding vibration and noise control. His research interests include noise and vibration control, active vibration and noise control, and nonlinear vibration.

Michael J. Brennangraduated from the Open University while he was serving in the Royal Navy. He received an MSc in Sound and Vibration Studies and a PhD in the active control of vibration, both from the University of Southampton, United Kingdom. He is a retired Professor of Engineering Dynamics at the Institute of Sound and Vibration Research (ISVR), the University of Southampton, UK, and is currently a Visiting Professor at UNESP, Ilha Solteira in Brazil. He is a past President of the European Association of Structural Dynamics, Associate Editor of the Transactions of the ASME Journal of Vibration and Acoustics and Guest Professor at Harbin Engineering University in China. He has a wide range of research interests, encompassing active and passive control of vibration, acoustics, vibroacoustics and rotor dynamics.

Zhigang Liuwas born in Shandong, China in 1956. He received his BS and MS degrees from Harbin Ship Engineering Institute in 1981 and 1987 respectively, and then received a PhD degree from Harbin Engineering University in 2000. Now he is the president of Harbin Engineering University and a professor and supervisor for PhD students. He is the vice-chairman of the Shipbuilding Industry Association of China, the Chinese Society of Naval Architects and Marine Engineers, the Science and Technology Association of Heilongjiang Province. He is also the executive director of Nuclear Industry Association of China and the Internal Combustion Engine Institute of China. He has authored and co-authored more than 100 journal and conference papers, one monograph on active vibration control of marine diesel. His main research interests include vibration and noise control, diesel dynamics,etc.

1671-9433(2014)03-0291-08

Received date: 2013-11-28.

Accepted date: 2014-06-04.

Foundation item: Supported by the National Natural Science Foundation of China (No. 51375103).

＊Corresponding author Email: yangtiejun@hrbeu.edu.cn

© Harbin Engineering University and Springer-Verlag Berlin Heidelberg 2014