王永恒

（上海中侨职业技术学院，上海，201316）

标量乘算法属于椭圆曲线运算中最耗时同时也是最为重要的运算之一，现阶段应用较为广泛的标量乘算法实现快速算法的方式包括二进制法、m-ary 方法以及NAF 编码等，其他还有窗口法和滑动窗口法等。本文对上述算法做了细致的阐释和讨论，并基于并行运算的理念，对于混合坐标下点加点倍中的运算序列进行了改进，以期能够给使运算序列高效实现并行运算。

1 椭圆曲线密码的研究意义

早在四千多年前，人们就已经开始在军事及外交通信中应用密码技术，然而其真正成为一门独立的学科则是在1949 年，由学者Shannon 在其撰写的“保密通信的信息理论”中被首次提出。在Shannon 提出之后，由于当时人们的大数分解能力，只需要使用不太大的模数，如RSA 算法就已经可以很安全，所以学界并没有立即将椭圆曲线密码当作一种理论上的选择，也未能引起人们的高度重视。但是即使如此，学界对于椭圆曲线密码的研究却一直再继续，随着研究的持续深入，人们开始总结出了一般的标量乘法，也就是IEEEPl363，该种算法无论是在速度上，还是在安全性方面均取得了重大突破。然而，随着攻击能力的逐渐增强，基域也越来越多，标量乘法的效率始终是椭圆曲线密码得以顺利应用的一个关键条件，人们对密码以及基于GAP 群的密码的研究和应用必须以高效的标量乘法作为基础。

新阶段，人们始终未停止过对安全高效的标量乘法的研究。不断加大对于椭圆曲线密码的研究力度，不仅具有重要的学术价值，也具有一定的现实意义。

2 椭圆曲线密码体制的优势

和RSA 体制和EIGamal 类体制体制比较，本文所探讨的椭圆曲线密码的优势主要包括以下几个方面：

第一，和所述其他两种体制相比，其具有最强的单比特安全性。

第二，假设基域完全相同的条件下，其能够拥有更多的可选择性。

第三，能够主动选取基域中的素数，从而能够有效选取更加有利于计算机处理的素数。

第四，其密钥和系统参数均相对较小。

第五，对于带宽的要求较低，适用性强。

3 椭圆曲线密码体制中标量乘算法的研究现状

椭圆曲线上点的标量乘法是椭圆曲线密码体制得以顺利实现的一个重要因素。所谓标量乘法，实际上就是在椭圆曲线上点P 以及一个大整数k 一定的条件下，计算kp 的大小，话句话说，就是通过椭圆曲线上加法来对P 和自身进行连续相加，相加次数为k 次。在实现椭圆曲线公钥密码体制的过程中，无论是加密环节，还是验证环节，其中均必须应用标量乘法。我们从近年来研究出的基于双线性对的密码体制来看，标量乘法也在其中充当了快速实现的基础。现阶段，计算标量乘算法的算法主要包括以下几种：常用的如二进制展开法、窗口法以及带符号的二进制法，其他还有m 进制法以及带符号的m 进制法等。而其中又以IEEE P1363 标准中所推荐使用的投影坐标条件下完全不连接形式的二进制法应用最为广泛，同时也是最快的算法。

作为一种经典且应用较为广泛的数学工具，椭圆曲线在密码学界的应用领域也较多，除了椭圆曲线公钥密码体系之外，在其他多种领域椭也同样发挥着重要作用。当前，椭圆曲线上的代数运算，无论是在硬件还是在软件上均得到了越来越高效的实现，也正是因为如此，人们对于利用椭圆曲线来构造伪随机序列的课题研究也越来越重视，并将其命名为椭圆曲线序列。

4 快速标量乘算法在椭圆曲线密码体制中的应用

4.1 攻击标量乘算法

实际上，椭圆曲线密码中最为基本的一个算法就是二进制算法，同时其也是近年来改进标量乘算法的一个最为基本的算法，其所遭受到的边信道攻击也成为影响改进成果的一个关键问题，而之所以造成这种攻击的主要原因，就在于标量乘的实现和密钥k 之间存在着密切的关系。在该算法中，倍点运算与点加运算二者实现所需要的计算量存在着很大的差异，因此也就导致不同能量曲线的存在。对于标量乘运算的能量曲线，采用运算的密钥就可以将其破解。

用k 可来代表唯一的二进制：

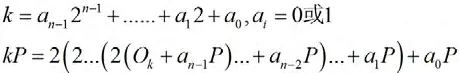
采取二进制算法

由此可以推测出标量乘运算的AD 序列：DAIDAIDIDAIDI...

最终可以计算出密钥为11010…

定义：如果攻击者可以借助一个单独的标量乘来计算出能量曲线区分点加和倍点，那么我们就可以认为攻击者具有了点加与倍点可区分，又可以称之为AD 可区分。

定理：分析二进制算法对于能量曲线实现的过程，可以得出AD 可区分的攻击者可以独立实现私钥k 的推出。

证明：通常情况下，点加与私钥的非零位之间存在着密切的关系。举例来说，在二进制算法中，(1101)2P=13P 所对应AD 序列是：ADADDA。其中，DA 和1 二者互为对应，独立的D 则和0 之间存在着对应关系：这个序列完成表明了私钥k=13。为了可以得到明确的私钥中非零位的具体区域，攻击者可以有效识别点加的能量信号，话句话说即：在能量曲线上可以有效分辨出点加与倍点所表现出来的不同形状。

4.2 标量乘算法的马尔科夫模型

关于攻击者的能力，可以做出一些假定，具体如下：

(1)假设标量乘运算的所有执行的边信道轨迹均能够获得：

(2)假设在轨迹中，可以清楚的分辨出点加运算与倍点运算；

(3)假设标量乘算法为已知。

首先，攻击者需要结合边信道轨迹而对出倍点以及点加序列做出较为准确的推测。可以使用{A，D)所构成的字母序列来进行表示，其中最左边的字母对应的运算应当是最先运行的。对于攻击者来说，其根本目标是利用在得到的AD 序列基础上而推测出私钥k。需要注意的是，由于相同的AD 序列所对应的私钥实际上是存在差异的，所以，其次就应当是确定出所有可能的密钥，形成密钥集合。再次，通过对密钥集合的观察和分析，来找到正确的密钥。

在这一过程中，对于条件概率的计算存在着较大的难度，其较为复杂。不过可以通过计算X 以及Y 的子序列来进行实现，其中还需应用到标量乘算法特殊状态中的概率问题。而对于这些概率的计算则可以利用马尔科夫链来进行。

计算中可以将标量乘算法视为马尔科夫链。

定义：假设T 表示的是k×k 矩阵，其中的元素用pij 来表示，同时满足1 ≤i，j ≤k 的条件。一个有限状态空间为｛s1，s2，......，sk｝的随机过程｛X0，X1，......｝，可以将其命名成转变矩阵为T 的马尔科夫链。

从中我们能够推出公式：

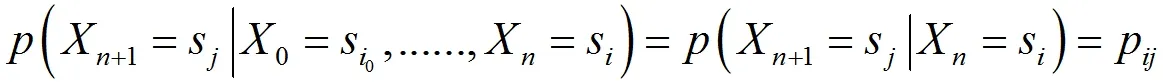
马尔科夫链状态间所进行的转变被随机变量决定，同时会以一定的概率的形式来出现，而这个概率可以是已知的，也可以是需要通过计算而得出的。马尔科夫链具有两个关键特征，一个是不可约性，一个是非周期性。前者表明了每个状态都能够在有限步在之内通过其他状态来实现。后者则表明所有状态实际上均没有周期。我们假设一个状态的周期是l，也就意味着这个状态属于非周期的，两者共同构成了马尔科夫链基本原理的重要条件。在对于这个基本原理进行描述之前，首先需要确定固定分布的概念：

定 义：令｛X0，X1，......｝是｛s1，s2，......，sk｝与T 之间的马尔科夫链。那么满足

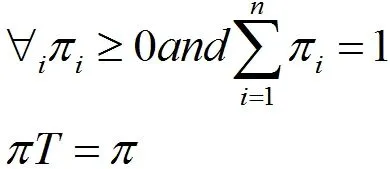
定理：所有不可约以及非周期马尔科夫链，均具有唯一的固定分布π 以及链的任意分布，如果n 趋近无穷时接近π，那么我们就可以判定这个与初始分布和之间不存在任何关系。从中我们可以看出马尔科夫过程带有不可约性以及非周期性两种性质。需要注意的是，该算法的初始条件应当满足马尔科夫过程的初始状态为（1，0，0）。

基于此，我们认为稳定状态仅为两个状态后达到，而马尔科夫过程则属于不可约的，究其原因，主要在于状态转变图中并不存在不连接的区域。由于其回到状态的概率都是正的，所以我们可以得出马尔科夫过程为非周期的。

4.3 马尔科夫链增强

(1)预计算阶段

首先，我们需要找到马尔科夫模型，接着再找到转变矩阵以及稳定状态向量，然而找到给定的标量乘算法。最后对于全部的X 和Y 组合的条件概率来进行分析和计算.

(2)数据收集阶段

主要是根据边信道轨迹情况来分析得出AD 序列.

(3)数据分析阶段

从已经得到的AD 序列中分成一些子序列，也就是我们通常所说的比特样品.

(4)密钥测试阶段

根据已知明文以及密文对，来对于前面所得出的全部比特样品的组合来进行测试。最后计算出短密钥。

由此可以得到以下定理:

定理：如果处于最坏的情况，那么我们就只需要关注非零条件概率。这种条件下，研究者至多测试的密钥数量为，测试的平均密钥数量为

定理：如果处于平均情况，那么就只需要关注条件概率。

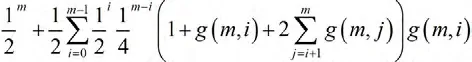
5 结语

ECC 是基于椭圆曲线上离散对数难题的一种公钥密码系统，然而从本质上来看，其只是已有密码体制的一个翻版，其单比特安全性远远超出其他密码体制。处于同样的安全强度条件下，和其他密码体制相比，其具有密钥长度短、计算量小以及存储量小等优势，其对于带宽需求不过。因而，当前ECC 在全球范围内均得到了广泛应用，被认为是本世纪最重要的一种公钥密码体制。

总之，ECC 的高比特安全性以及低内存、低带宽要求等优势满足了当代社会对便携设备安全性的需要，今后随着人们对其物理安全性关注度的日益提高，对于边信道攻击中的能量攻击对标量乘法所构成的安全性威胁也越来越重视，能量攻击能够避开算法数学层的安全性，而直接通过硬件本身的能量消耗发挥作用，进而对设备内部的密码系统构成不同程度的攻击。在这种情况喜爱，研究ECC 的快速实现以及抵抗边信道攻击中的能量攻击，对进一步促进ECC 的推广应用具有十分重要的作用。

[1] Katsuyuki Okeya and Tsuyoshi Takagi.The width-W NAF method provides small memory and fast Elliptic Scalar multiplications secure against side channel attacks[J].CT-RSA2003，LNCS 2612,pp 328～343.Springer-Verlag,2003.

[2] Chae Hoon Lim ANew Method for Securing Elliptic Scalar Multiplication Against Side-Channel Attacks[J].ACISP 2004，LNCS 3108,pp 89-300. Springer-Verlag Berlin Heidelberg,2004.

[3] 郝林,罗平.椭圆曲线密码体制中点的数乘的一种快速算法[J].电子与信息学报,2003,25(2)：275～278.

[4] 韩军,曾晓洋,汤庭鳌.RSA 密码算法的功耗轨迹分析及其防御措施[J].计算机学报,2006,29(4)：590～596.

[5] 刘铎,戴一奇,王道顺.平稳与平衡一椭圆曲线密码体制抗旁信道攻击的策略与手段[J].计算机研究与发展,2005,42(10)：1667～1672.