江小霞，王颂生，毛 渝，许 娣

(江西师范大学数学与信息科学学院，江西 南昌330022)

1 引言和预备知识

在半模范畴，半模的正合列的定义一般有2种，一种是利用元素的观点，另一种是利用同余的观点。文献［2，3］采用了同余观点定义的半模正合列。这里采用另一定义，即文献［1］中半模正合列的定义，得到比文献［2，3］更完善的结论，如定理1。同时，将文献［4，5］中模的正合列的性质推广到半模中。文中半环和半模的定义均出自文献［6］。

定义1:设M为左R-半模，且a∈M。若对于任意b，c∈M，由a+b=a+c可推出b=c，则称a为M中的可消元。如果M中所有的元素都是可消的，则称M为可消半模。

定义2:设A是半模，且B是A的一个子半模。若对于任意x∈A以及任意y∈B，由x+y∈B可推出x∈B，则称B是A的可减子半模。

设A和B是R-半模，f∶A→B是半模同态，给出记号

定义3:记号如上，若ρkerf是A上最小同余，则称f为单同态;若对于任意b∈B，∃ai∈A(i=1，2)和x∈B，使得b+f(a1)+x=f(a2)+x，则称f为epic;若对于任意b∈B，∃a∈A，使得f(a)=b，称f是满同态;若f既是单同态又是epic，则称f是equivalance;若f既是单同态又是满同态，则称f是同构;若f(A)=Im f，则称f是i-正则的;对于任意a，a'∈A，如果由f(a)=f(a')可以推出存在k，k'∈Kerf，使得a+k=a'+k'，则称f是k-正则的;若f既是i-正则的，又是k-正则的，则称f是正则的。

定义4［1］:设有非零R-半模Mi及半模同态fi组成的一个序列

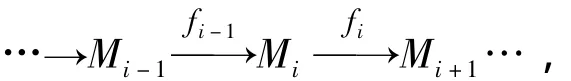
若对所有的 i，均有≡fi－1(Mi－1)=ρkerfi，则称这个序列为正合列。

命题5［1］:设A、B和C是R-半模，f和g是半模同态，则

命题8(因子定理［7］):设M，M'，N'，N是左R-半模，且设f∶M→N是R-半模同态:

(1)设g∶M→M'是k-正则满同态且满足Kerg⊆Kerf，则存在唯一的半模同态h∶M'→N，使得f=gh。

(2)设g∶N'→N是i-正则单同态且满足Im f⊆Im g，则存在唯一的半模同态h∶M→N'，使得f =gh。

2 半模正合列的性质

定理1:设A，Ai(i=1，2)，A'i(i=1，2)均为左R-半模。若下列图表交换，且水平和垂直方向的序列均为短正合列，则

(1)α，β均为零同态;

(2)f为equivalance;

(3)g为同构。

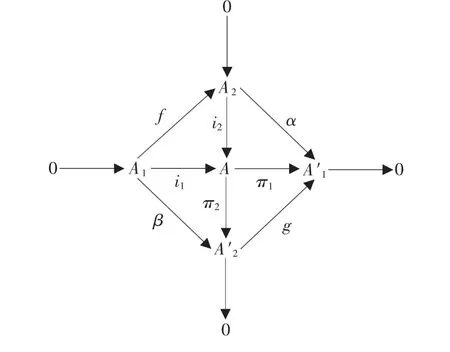
证明:(1)设a2∈A2是任意元。显然π2i2(a2)=0。又由于α=gπ2i2，所以α(a2)=gπ2i2(a2)=0，即有α=0。

同理可证β也是零同态。

(2)先证f是单同态。设a1，a2∈A1是任意元。若f(a1)=f(a2)，从而有i2f(a1)=i2f(a2)。由于i1=i2f，所以i1(a1)=i1(a2)。又由于i1是单同态，从而有a1=a2。由定义3知，f为单同态。

再证f为epic。设a2∈A2是任意元。由于α为零同态，从而α(a2)=0。又由于α=π1i2，所以π1i2(a2)=0。由此推出(i2(a2)，0)∈ρkerπ1=≡i1(A1)。因此，∃b1，b2∈A1，使得i2(a2)+i1(b1) =i1(b2)。由于i1=i2f，从而有i2(a2)+i2f(b1) =i2f(b2)，即i2(a2+f(b1))=i2f(b2)。又由于i2是单同态，从而有a2+f(b1)=f(b2)。由定义3知，f为epic。

(3)先证g为单同态。设a'1，a'2∈A'2是任意元。若g(a'1)=g(a'2)∈A'1，又由于π2是满同态，因此，∃a1，a2∈A，使得a'1=π2(a1)，a'2= π2(a2)。由此推出gπ2(a1)=gπ2(a2)。由于π1=gπ2，从而有π1(a1)=π1(a2)。由此推出(a1，a2)∈ρkerπ1=≡i1(A1)。因此，∃a3，a4∈A1，使得a1+i1(a3)=a2+i1(a4)。由此推出π2(a1)+π2i1(a3)=π2(a2)+π2i1(a4)。又由于π2i1=β=0，从而有π2(a1)=π2(a2)，即a'1=a'2。

再证g满同态。设a'1∈A'1是任意元。由于π1是满同态，因此，∃a1∈A，使得a'1=π1(a1)。又由于π1=gπ2，从而有a'1=g［π2(a1)］。由定义3知，g为满同态。

推论2:给定R-半模和R-同态的交换图表。

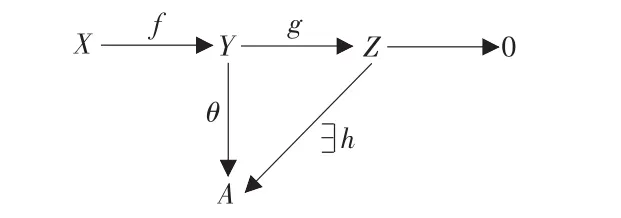
若行是正合的，并且θf=0，g(Y)是Z的可减子半模，则存在唯一R-的同态h∶Z→A，使得hg=θ。

证明:由命题5易知，g为满同态。现只要证g是k-正则的和Kerg⊆Kerθ。先证g是k-正则的。设y1、y2∈Y是任意元。若g(y1)=g(y2)，从而有(y1，y2)∈ρKerg=≡f(X)。因此，∃x1，x2∈X，使得y1+f(x1)=y2+f(x2)。又由于gf(x1)=gf(x2) =0，从而有f(x1)、f(x2)∈Kerg。由定义3知，g是k-正则的。再证Kerg⊆Kerθ。设y∈Kerg是任意元。显然g(y)=0，从而有(y，0)∈ρKerg=≡f(X)。因此，∃x1，x2∈X，使得y+f(x1)=f(x2)，θ(y)+θf(x1)=θf(x2)。又由于θf=0，所以θ(y) =0，从而有y∈Kerθ，即Kerg⊆Kerθ。由因子定理知，存在唯一的R-同态h∶Z→A，使得hg=θ。

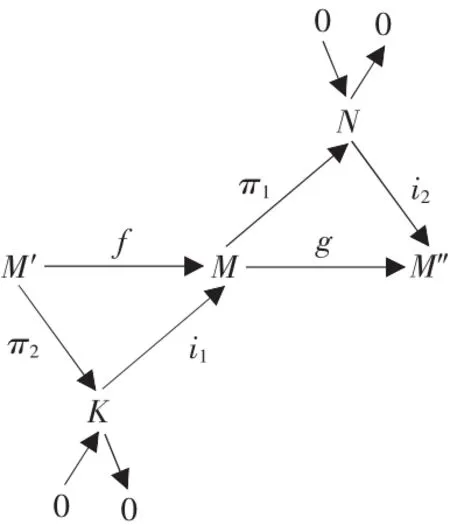
因为π2是epic，所以∃bi(i=1，…，4)∈M'，使得k1+π2(b1)=π2(b2)，k2+π2(b3)=π2(b4)。因此，i1(k1)+i1π2(b1)=i1π2(b2)，i1(k2)+i1π2(b3)=i1π2(b4)。又由于f=i1π2，从而有i1(k1) +f(b1)=f(b2)，i1(k2)+f(b3)=f(b4)，所以i1(k1)+f(b1)+f(b4)=i1(k2)+f(b2)+f(b3)。联合式(1)及半模M可消，从而有m1+f(b2+b3)= m2+f(b1+b4)，即(m1，m2)∈≡f(M')。

定理4:设下列R-半模和R-同态的图表可交换，并且上下行正合，B'，C，C'是可消半模。

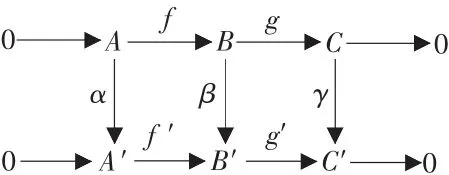
若β是同构，则有

(1)α是单同态;

(2)γ是epic;

(3)α是epic当且仅当γ是单同态。

证明:(1)设x，y∈A是任意元。若α(x)=α (y)，由于f'α=βf，从而有βf(x)=βf(y)。又由于β是同构，所以f(x)=f(y)。又因为f是单同态，从而有x=y。由定义3知，α是单同态。

(2)设c'∈C'是任意元。由于g'是epic，因此，∃b'1，b'2∈B'，使得

又因为β是同构，所以，∃bi(i=1，2)∈B，使得b'1=β(b1)，b'2=β(b2)。由此推出g(b'1)=g'β (b1)，g(b'2)=g'β(b2)。代入式(2)，有g'β(b2) =g'β(b1)+c'，又由于g'β=γg，所以γg(b2)= γg(b1)+c'。由定义3知，γ是epic。

(3)设x，y∈C是任意元。若γ(x)=γ(y)，由于g是epic，因此，∃bi(i=1，…，4)∈B，使得x +g(b1)=g(b2)，y+g(b3)=g(b4)。由此推出

将两式相加有γ(x)+γg(b1+b4)=γg(b2+b3) +γ(y)。由于γ(x)=γ(y)式，及半模C'可消，从而有γg(b1+b4)=γg(b2+b3)。又因为g'β= γg，所以g'β(b1+b4)=g'β(b2+b3)。由此推出(β(b1+b4)，β(b2+b3))∈ρkerg'=≡f'(A')，因此，∃a'i(i=1，2)∈A'，使得

由于α是epic，因此，∃ai(i=1，…，4)∈A，使得a'1+α(a1)=α(a2)，a'2+α(a3)=α(a4)。所以f'(a'1)+f'α(a1)=f'α(a2)，f'(a'2)+f'α(a3)= f'α(a4)。因为f'α=βf，所以

将式(4)、(5)相加得到f'(a'1)+βf(a1+a4)=βf (a2+a3)+f'(a'2)再联合式(2)得β(b1+b4)+f' (a'1)+f'(a'2)+βf(a2+a3)=β(b2+b3)+f' (a'1)+f'(a'2)+βf(a1+a4)。由于半模B'可消，因此βf(a2+a3)+β(b1+b4)=βf(a1+a4)+β (b2+b3)。又由于β是同构，从而有f(a2+a3)+ b1+b4=f(a1+a4)+b2+b3。由此推出gf(a2+ a3)+g(b1+b4)=g(b2+b3)+gf(a1+a4)。由于gf=0，从而有g(b1+b4)=g(b2+b3)。又由于x+g(b1+b4)=g(b2+b3)+y，及半模C可消，所以x=y。

反之，设a'∈A'是任意元。显然f'(a')∈B'。由于β是同构，因此，∃b1∈B，使得f'(a')=β (b1)。所以g'f'(a')=g'β(b1)。又由于g'f'=0，所以g'β(b1)=0。因为g'β=γg，所以γg(b1)= 0。由于γ是单同态，从而有g(b1)=0。由此推出(b1，0)∈ρkerg=≡f(A)，因此，∃ai(i=1，2)∈A，使得b1+f(a1)=f(a2)，从而有β(b1)+βf(a1)= βf(a2)。又由于βf=f'α，从而有β(b1)+f'α(a1) =f'α(a2)。又因为β(b1)=f'(a')，所以f'(a') +f'α(a1)=f'α(a2)。由于f'是单同态，从而有α (a2)=α(a1)+a'。由定义3知，α是epic。

［1］ 甘爱萍，黄福生.半模正合列［J］.江西师范大学学报，2003，27(2):131－134.

［2］ 敖忠平，蔡述平，宋海燕.半模的Z-同态与正合列［J］.新疆师范大学学报(自然科学版)，2007，26 (4):18－21.

［3］ 敖忠平，蔡述平，宋海燕.可消半模的五引理［J］.新疆师范大学学报(自然科学版)，2008，27(2):12－14.

［4］ Blyth T S.模论-对线性代数的一种处理［M］.广州:广东民族学院，1976:5.

［5］ Anderson F W，Fuller K R.Rings and categories of Modules［M］.New York:Springer-Verlag，1973.

［6］ Golan J S.The Theory of Semirings with Applications in Mathematics and Theoretical Computer Science［M］.Exxes，England:Longman Scientific＆Technical，1999.

［7］ Al-Thani H M J，k-projective semimodules［J］.Kobe J.Math.，1996，13(1):49－59.