齐 鹏，孙建国

(吉林大学地球探测科学与技术学院，吉林长春130026)

近年来，随着计算机硬件水平的不断提高，地震波数值模拟进入高精度时代，三维数值模拟已逐渐成为常规的地震波场数值模拟技术。但是，在处理大尺度数值模拟或是快速计算时，由于计算效率的限制，三维数值模拟的高效实现仍存在一些困难。而传统的二维数值模拟由于未考虑三维几何扩散，导致模拟的地震波振幅信息存在较大误差，只能较准确地反映地震波的运动学特性，模拟精度较低。为了在保证计算效率的同时又能保证模拟的准确性，2.5维数值模拟得到了很大的发展[1]。2.5维数值模拟假设三维介质沿走向方向不变，使用三维震源在计算平面内研究地震波的传播，可以得到较精确的地震波动力学信息，特别是针对具有沿走向方向稳定变化特点的沉积岩层褶皱、断层或其它含油气地质构造，作为三维问题的一种特殊情况，2.5维模拟是一种很好的折中手段[3]。

鉴于声波模型是反射地震偏移成像理论和应用研究中的基本数据模型，所以对2.5维声波方程数值模拟的研究具有重要意义。目前，2.5维声波方程数值模拟主要采用两种方法：Fourier变换法[2]和近似方程法[3-6]。其中，Fourier变换法是对于三维声波方程的沿走向方向做Fourier变换，得到关于波数k的二维声波方程，对不同波数k的二维方程进行数值模拟，再通过叠加得到2.5维数值模拟的结果，相当于进行多次二维数值模拟，计算量较大；而近似方程法是通过某些近似条件推导出不同形式的2.5维的声波近似方程，再求解近似方程，相当于一次“二维数值模拟”，相对于Fourier变换法具有更高的计算效率。考虑到近似方程法在计算速度上的优越性，本文中采用近似方程法。

针对2.5维声波近似方程的推导，人们利用不同的近似条件得到了不同形式的近似方程。Liner[3]将匀速介质中的三维Green函数带入二维声波方程，得到常密度条件下L型2.5维声波近似方程。Williamson等[4]对二维波场施加一个滤波器，获得与L型方程末项不同的W型2.5维声波近似方程。Narayan[5]通过对比L型方程和W型方程的数值模拟结果，得出两个方程末项可缺省的结论，得到DL型方程。我们选用Liner提出的L型近似方程进行起伏地表条件下2.5维声波数值模拟。

此外，在实际的地震勘探工作中，经常会遇到复杂条件的起伏地表问题，起伏地表下地震波传播问题的研究在地震学和勘探地震学领域具有重要意义[7-9]。起伏地表的地震波数值模拟方法很多，其中处理效果较好的有限元法[10]存在计算效率不高、网格生成复杂的缺点，边界元法不适合模拟复杂地质模型；而Tessmer等[11]提出了坐标变换法可以将有限差分法应用于起伏地表的数值模拟，具有很高的计算效率，而且能保证精度；Hestholm等[12-13]利用坐标变换法实现了基于应力-速度一阶弹性波方程的起伏地表二维和三维数值模拟；唐文等[14]实现了基于二阶弹性波方程的起伏地表数值模拟；王祥春等[15]采用类似的坐标变换实现了二维声波方程的起伏地表数值模拟。

相对于应力-速度一阶弹性波方程和二阶弹性波方程可以模拟起伏地表产生的散射波、转换波等各种复杂现象，起伏地表问题对声波数值模拟的动力学特征会产生很大影响，值得研究探索。同时，作为现阶段地震数据采集和处理的基本数据模型，针对起伏地表问题的声波方程数值模拟同样具有现实意义。考虑到2.5维数值模拟具有兼顾模拟精度和计算效率的优势，我们将坐标变换法引入到起伏地表2.5维声波方程数值模拟中，推导出映射坐标系下的2.5维L型声波近似方程；采用有限差分法，实现起伏地表条件下2.5维声波方程的数值模拟；并通过与起伏地表二维声波方程数值模拟结果的对比，来验证起伏地表2.5维声波方程有限差分数值模拟方法的有效性。

1 时间域2.5维声波近似方程

如图1所示，2.5维问题是三维问题的一种特殊情况。2.5维问题假设介质条件沿走向(图1中y方向)不变，震源使用三维震源，且与检波点位于垂直于走向的同一条直线上(图1中y=0的x-z平面内)时，就可以把三维数值模拟问题近似为一个2.5维数值模拟问题。这样，2.5维地震波数值模拟既保留了三维地震波的传播特点，又具有二维地震波数值模拟有较高计算效率的优点，可以说是三维数值模拟的一种很好的折中手段。

图1 2.5维地质模型示意图解

2.5维波动方程数值模拟的基础是采用什么形式的2.5维波动方程，关于该问题Liner[3]假设在常密度介质条件下，2.5维Green函数是某一空间方向延伸为0(例如y轴方向)的三维Green函数，即2.5维Green函数相当于是三维Green函数的一个空间“切片”，表达式为

(1)

(2)

(3)

从左到右各项依次表示平面内的二维波动方程、平面外振幅随时间衰减的散射方程及平面内的保幅谐振子方程。方程(3)即为本文要求解的L型2.5维声波方程。

2 坐标变换法

坐标变换法的基本思想如图2所示，通过坐标变换将物理空间(x-z)域内的起伏地表问题，转化为计算空间(ξ-η)域内的水平地表问题[15]。即对起伏地表条件下的L型2.5维声波近似方程进行坐标变换，利用有限差分法求解坐标变换后的方程，再将计算结果映射回起伏地表条件，实现起伏地表条件下2.5维声波方程有限差分法数值模拟。

图2 物理空间(x-z)域内的起伏地表(a)及计算空间(ξ-η)域内的水平地表(b)

坐标变换法的关键是选取合理的映射函数，我们选取的映射函数为[12]

(4)

式中：(x,z)为物理空间内的起伏地表坐标系；(ξ,η)为计算空间内的水平地表坐标系；z0(ξ)为描述地表起伏的函数；ηmax为(ξ,η)坐标系内垂直方向的最大坐标；zmax为(x,z)坐标系内垂直方向的最大坐标。

为推导计算空间内的2.5维声波方程，首先对物理空间内起伏地表条件下的波场p关于x(或z)的一、二阶偏导作如下变换。

求取波场p对x方向的一、二阶偏导：

(5)

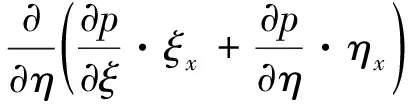
(6)

求取波场p对z方向的一、二阶偏导：

(7)

(8)

式中：ξx，ηx，ξz和ηz是方程变换过程中的变换系数。由坐标映射式(4)得

(9)

将(6)式、(8)式和(9)式代入(x-z)坐标系下的2.5维L型方程(3)，得到映射坐标系(ξ-η)下的2.5维L型声波近似方程：

(10)

此外，由于2.5维声波近似方程法是通过对二维声波方程添加校正项，修改振幅、波形和波前等来模拟三维地震波场的，所以本文中采用二维起伏地表声波方程的单程波动方程边界条件[15]。由于4个方向的边界条件及4个角点边界条件相似，这里只给出左边界条件及左上角点边界条件。

左边界条件：

(11)

左上角边界条件：

(12)

其中，c1=1.05086，c2=0.75147。

至此，给出了映射坐标系下的2.5维L型声波近似方程(10)，边界条件(11)和(12)，下面我们将详细阐述如何采用有限差分格式来离散这些方程和边界条件。

3 数值实现

通过以上的坐标变换得到了计算空间内的2.5维L型声波近似方程及边界条件，即水平地表条件下的规则网格2.5维问题。本文中采用有限差分法，以“差分代替微分”，建立并求解差分方程，来实现数值模拟。如图3所示，根据网格点位置建立差分方程。

图3 2.5维声波方程及边界条件的离散示意图解

在网格内部非边界上的网格点(如图3中的点1)，对时间和空间的二阶导数采用二阶中心差分格式，对空间的一阶导数采用一阶中心差分格式，对时间的一阶导数采用一阶向前差分格式即：

(13)

式中：x，z方向的网格间距均为h；Δt为时间步长；l，m是水平和垂直方向的网格指数；n是时间指数。然后将(13)式代入方程(10)，得到内部网格点的差分方程：

(14)

式中：Ex,z=vx,z·Δt/h；vx,z代表声波速度，是网格位置x，z的函数；T=Δt/t，t为旅行时。

在网格边界及角点处(如图3中的点2或点3)，同理利用边界条件和角点条件得到差分方程[15](此处只给出左边界条件及左上角点边界条件)。

左边界条件:

(15)

左上角点条件：

[p(l,m+1,n)-p(l,m+1,n-1)-

p(l,m,n)+p(l,m,n-1)]+E(l,m)·

n-1)-p(l,m,n)+p(l,m,n-1)]-

p(l,m+1,n)-p(l+1,m,n)+p(l,m,n)]-

[p(l,m,n-1)-2p(l,m,n)]

(16)

通过以上的差分方程可以得到计算空间内的各网格点的声压值。最后，通过映射函数((4)式)将计算空间内(ξ-η)坐标系下得到的声压值逆映射到物理空间内(x-z)坐标系下的声压值，完成起伏地表条件下2.5维声波方程的有限差分数值模拟。

4 数值算例及分析

4.1 均匀介质模型

为了验证起伏地表对直达波的影响，选取一个起伏地表的均匀介质模型，如图4所示。地表函数为正弦函数z0=50sin(πx/125+π/2)+50。模型大小为1000m×1100m，网格间距为5m，采样时间为0.4s，时间步长为0.1ms，震源为主频30Hz的雷克子波，震源位于模型中间地表以下50m处。

图4 起伏地表均匀介质模型

对起伏地表均匀介质模型应用2.5维声波方程有限差分数值模拟给出的直达波示于图5，可以看出，起伏地表对直达波场具有很大影响，检波器接收到的直达波场呈现出与地表条件吻合的形状。

4.2 层状介质模型

为进一步考察起伏地表条件下2.5维反射波场的传播，建立了一个3层的起伏地表层状介质模型(图6)，与起伏地表均匀介质模型具有相同的地表函数，3层介质的速度参数分别为1500，2000，2500m/s。除了采样时间为1s外，其它模拟参数均与上述均匀介质模型的数值模拟相同。

图5 起伏地表均匀模型模拟的直达波

应用起伏地表条件下2.5维声波方程有限差分数值模拟方法对起伏地表层状介质模型模拟出的反射波场如图7所示。从图7中可以发现，检波器在0.4s左右接收到第1个反射界面的反射波，在0.7s左右接收到第2个反射界面的反射波；反射波场的形状与起伏地表正弦函数的形状吻合；存在少量频散。

图6 起伏地表层状介质模型

图7 起伏地表层状模型模拟的直达波

4.3 与二维模拟结果的对比

为了验证2.5维数值模拟较二维数值模拟在模拟地震波动力学特征(振幅)方面的优势，对起伏地表条件下2.5维声波近似方程数值模拟与起伏地表条件下二维声波方程数值模拟的结果进行对比分析。选取起伏地表双层介质模型如图8所示。

起伏地表条件下2.5维声波方程和二维声波方程模拟出的反射地震波场如图9所示。对比可见，2.5维(图9a)与二维(图9b)模拟地震记录的反射波接收时间基本一致。为了更精确的对比，选取两张记录中的第50道(横坐标250m处，炮检距为250m)叠合放大如图10a所示。分析图10a可以得到几点认识：①2.5维与二维单道模拟记录只是在振幅上存在差异，在时间上完全吻合，这就证明了本文中2.5维声波方程数值模拟方法的正确性；②二维模拟的反射波振幅(虚线)明显大于2.5维模拟的反射波振幅(实线)，这是因为二维声波方程数值模拟没有考虑三维球面几何扩散，使得二维数值模拟的地震波动力学特征(振幅)数值偏大，偏离了实际的地震-地质情况；③2.5维数值模拟得到地震波传播时间特性与二维模拟结果具有相同的精度，模拟的地震波振幅特性比二维数值模拟更接近地震波的空间传播特性，可见2.5维数值模拟相较于二维数值模拟更具优势。

图8 起伏地表双层介质模型

为进一步验证起伏地表条件下2.5维声波方程数值模拟的衰减特性，选取位于炮点右侧第40道(横坐标200m处，炮检距为300m)的2.5维与二维模拟单道记录叠合放大示于图10b。与图10a

图9 起伏地表双层模型的2.5维(a)和二维(b)模拟地震记录

图10 起伏地表双层模型2.5维(实线)与二维(虚线)模拟结果的第50道(a)和第40道(b)记录

对比可以发现，随着炮检距增大，2.5维与二维模拟响应的振幅都逐渐减小，但2.5维声波模拟响应振幅的降低幅度明显大于2维模拟响应振幅降低的幅度，这就验证了2.5维声波方程数值模拟在时间和空间上的衰减特性。

5 结论与认识

基于Liner提出的2.5维L型声波方程，采用坐标变换的方法，实现了起伏地表条件下2.5维声波近似方程的有限差分法数值模拟。通过理论模型试算，将该方法与二维起伏地表条件下声波方程数值模拟方法作对比，发现两者的模拟结果在地震波运动学特征上基本一致，而在地震波动力学特征上存在差异，证实了本文给出的起伏地表2.5维声波方程数值模拟方法相较于二维声波方程数值模拟方法在模拟地震波动力学特征上更有优势。同时，通过不同炮检距模拟记录的振幅对比，验证了2.5维声波方程数值模拟在时间和空间上的衰减特性。研究结果表明，2.5维声波方程数值模拟可以很好地处理起伏地表问题，在模拟精度和计算效率方面都是三维数值模拟的一种很好的折中方法。

参 考 文 献

[1] 孙建国.2.5维地震波数值模拟评述:声波模型[J].地球物理学进展,2009,24(1):20-34

Sun J G.A review of 2.5 dimensional seismic modeling methods:acoustic case[J].Progress in Geophysics,2009,24(1):20-34

[2] Novais A,Santos L T.2.5-D finite-difference solution of the acoustic wave equation[J].Geophysical Prospecting,2005,53(4):523-531

[3] Liner C L.Theory of a 2.5-D acoustic wave equation for constant density media[J].Geophysics,1991,56(12):2114-2117

[4] Williamson P R，Pratt P R.A critical review of acoustic wave modeling procedures in 2.5 dimensions[J].Geophysics,1995,60(2):591-595

[5] Narayan J P.2.5-D numerical simulation of acoustic wave propagation[J].Pure and Applied Geophysics,1998,151:47-81

[6] 李芳，孙建国，王雪秋,等.2.5维声波数值模拟[J].吉林大学学报(地球科学版),2006,36(增刊):177-181

Li F,Sun J G,Wang X Q.Numerical simulation of 2.5D acoustic waves[J].Journal of Jilin University(Earth Science Edition),2006,36(S1):177-181

[7] 孙建国.复杂地表条件下地球物理场数值模拟方法评述[J].世界地质,2007,26(3):345-362

Sun J G.Methods for numerical modeling of geophysical fields under complex topographical conditions:a critical review[J].Global Geology,2007,26(3):345-362

[8] 杨海生.起伏地表波动方程波场延拓起始面研究[J].石油物探,2009,48(1)：66-71

Yang H S.Study on staring datum of wave equation wave field continuation for rolling surfaces[J].Geophysical Prospecting for Petroleum,2009,48(1):66-71

[9] 孙章庆,孙建国.2.5维起伏地表条件下坐标变换法直流电场数值模拟[J].吉林大学学报(地球科学版),2010,40(2):425-431

Sun Z Q,Sun J G.2.5-D DC electric field numerical modeling including surface topography based on coordinate transformation method[J].Journal of Jilin University(Earth Science Edition),2010,40(2):425-431

[10] 郭宏伟,王尚旭，孙文博.基于非均质体的波动方程有限元正演模拟[J].石油物探，2012,51(4):319-326

Guo H W,Wang S X,Sun W B.Wave equation modeling by finite-element method for heterogeneous body[J].Geophysical Prospecting for Petroleum,2012,51(4):319-216

[11] Tessmer E,Kosloff D.3-D elastic modeling with surface topography by a chebychev spectral method[J].Geophysics,1994,59(3):464-473

[12] Hestholm S,Ruud B.2-D finite-difference elastic wave modeling including surface topography[J].Geophysical Prospecting,1994,42(5):371-390

[13] Hestholm S,Ruud B.3-D finite-difference elastic wave modeling including surface topography[J].Geophysics,1998,63(2):613-622

[14] 唐文，王尚旭，袁三一.起伏地表二阶弹性波方程差分策略稳定性分析[J].石油物探，2013,52(5)：457-463

Tang W,Wang S X,Yuan S Y.Stability analysis of differential strategy for rugged by second-order elastic wave equation based on coordinate transformation[J].Geophysical Prospecting for Petroleum,2013,52(5):457-463

[15] 王祥春，刘学伟.起伏地表二维声波方程地震波场模拟与分析[J].石油地球物理勘探,2007,42(3):268-276

Wang X C,Liu X W.Simulation an analysis of seismic wavefield in relief surface by 2D acoustic wave equation[J].Oil Geophysical Prospecting,2007,42(3):268-276