王鑫, 袁晓光, 杨星

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.西安电子科技大学 电子工程学院, 陕西 西安 710071

主要符号定义

飞行器携带特种分离载荷的飞行任务模式目前成为航空航天领域一个研究的热点。此类飞行器在大气层内飞行,在大纵深预定的目标区域上空将有效载荷分离释放,以完成侦查、打击、预警、数据通讯、热点区域监视等任务[1]。此类任务中有效载荷作为分离体从运载平台脱离的过程中,由于仍在大气层中,因此其多体分离过程与传统航天器在真空环境下的抛罩分离过程显著不同[2]，分离过程的气动和姿态动力学特性将直接影响到分离体后续的飞行态势。

在此类飞行器分离体的气动仿真工作中,需要涉及到多体动力学微分方程的求取与计算,可以应用拉格朗日力学方法来建立飞行器运动过程的状态方程,并进行多体动力学模型的简化和求解[3]。拉格朗日力学是分析力学的一种,是对经典力学的一种新的数学表述,其引入了广义坐标的概念,并运用达朗贝尔原理得到与牛顿第二定律等价的拉格朗日方程。拉格朗日方程在多体系统领域具有更普遍的意义和更广泛的适用范围;并且在选取恰当的广义坐标后,可以使多体动力学方程得到简化,其微分方程形式规范,物理意义明确[4]。

本文研究的飞行器在近空间大气层内抛离头部的有效载荷，飞行器本体和有效载荷分离体将作为一个多体系统来考虑。在整个分离过程中,忽略瞬时分离火工品的作用(相比分离过程而言,时间很短),则分离体仅受分离过程前后的重力和气动力的作用。由于在气动环境下分离体的姿态特性将对飞行器的飞行态势产生重要影响,本文重点研究如何使用拉格朗日力学方法计算出分离体的姿态参数变化情况。

1 分离体模型建立

1.1 建立动力学模型

分离体与飞行器分离之后,没有自主的动力,只受气动力和重力的作用，其中气动力为外力,重力是与势能相关的力。以分离体作为研究对象的动力学系统可视为非保守系统,并假设分离体运动过程中不受约束,或认为受到常值的定常约束。分离方式及坐标系定义见图1。

图1 有效载荷分离方式及坐标系示意图

1.2 坐标系选取

1) 惯性参考系

如图1所示,取分离体与飞行器初始分离时刻为t=0时刻。选取惯性参考系AX0Y0Z0,与地球固联。原点A取t=0时刻分离体质心O在地面投影。AX0轴在水平面内,取t=0时刻分离体速度在水平面内投影为正;AY0轴与地面垂直,向上为正;AZ0轴按右手定则确定。

2) 本体动坐标系

取本体坐标系OXYZ固联于分离体本体,原点O与分离体质心重合;初始时刻t=0各轴方向规定如下:AX轴在水平面内,取初始速度在水平面内投影方向为正;AY轴垂直于水平面,向上为正;AZ轴按右手定则确定。本体坐标系随分离体的位置和姿态的变化而变化。

2 拉格朗日广义坐标与广义力的选取

广义坐标是用以确定系统位形的一组独立参变数,坐标的选择通常是直观的并决定于系统的特征,所以可选择合适的系统变量构建广义坐标。拉格朗日方程采用广义坐标来描述完整约束系统,对于简化方程的求解有很大帮助,本文所研究的情况虽没约束存在,但引入广义坐标概念,可方便采用不同参数、更好地运用拉格朗日方程。

根据广义坐标的性质,一个系统需要设定的广义坐标数目,等于该系统的自由度数目。针对本文中研究的分离体拥有6个自由度,对应地需要定义6个适当的广义坐标来描述该系统。

6个广义坐标设为q(q1,q2,q3,q4,q5,q6),其中r(q1,q2,q3)亦表示为r(x,y,z),分别表示本体坐标系相对于惯性参考系AX0Y0Z0轴上的位置坐标值;θ(q4,q5,q6)亦表示为θ(α,β,γ),分别表示本体坐标系相对于惯性参考系的3个姿态角是由本体系依次绕OX、OY、OZ轴旋转相应角度得到。

此外定义与广义坐标相对应的广义力,记为Qj;根据拉格朗日力学分析,广义力的数目等于广义坐标的数目。当qj的量纲是长度时,Qj的量纲就是力的量纲;当qj的量纲是角度时,Qj的量纲就是力矩的量纲,于是Q1～Q3为系统所受力F的广义形式,Q4～Q6为力矩M的广义形式。

3 建立分离体姿态动力学方程组

3.1 广义坐标简化

对分离体姿态动力学推导之前,有必要先引入拉格朗日方程的有关结论及公式。拉格朗日方程如下:

(1)

式中：

(2)

系统实速度的广义坐标表示式:

(3)

式中：

ri=ri(q1,…,q6,t)

(4)

根据拉格朗日力学理论,当系统只有定常约束的情况下,(4)式将不显含t。本文假设分离后的有效载荷仅受重力和气动力,故分离过程可视为只有恒为零的定常约束动力学过程,故(3)式可简化成为:

(5)

3.2 分离体的拉格朗日动力学方程

分离体动力学方程需要选取合适的广义坐标来表示系统动能T,本文分离动力学模型的系统动能T可表示为:

(6)

代入(5)式及角速度的广义坐标表达式,即:

式中：

需要注意到由于存在坐标系转换,本文分离体的姿态角是指机体坐标系相对惯性系的角度,其导数也是相对惯性系而言[5];而分离体的角速度则是绕机体坐标系3个坐标轴旋转的速度,是相对于机体坐标系而言的,这点不等同于姿态角的单纯导数。

根据本文广义坐标的选取规则可得出,表示位置关系的矢径r可用广义坐标标记为:

(7)

在(6)式系统动能表达式中,可将动能分为两部分,即Tv和Tω,分别表示为分离体质心平动和绕质心转动的动能,分别由(8)式和(9)式表示:

(8)

(9)

至此系统动能T已变为由广义坐标qj表示的形式,再将T的广义坐标表达式代入(1)式后可得:

(10)

分离体的姿态角和角速度解算采用如下方程：

(11)

式中：

(12)

经过上述方程的变换,可化为分离体所受力和力矩与广义坐标的方程。最终可得包含6个广义坐标的力和力矩的方程组形式如下:

(13)

4 数值求解及仿真结果分析

4.1 分离姿态信息的数值求解

上节中得出了微分方程形式的分离体姿态动力学方程组,建立了分离体所受力和力矩与分离体的速度、角速度关系的模型,可以用于分离体由所受力和力矩来计算和估计自身的位置信息和姿态信息。实际仿真实验中,由于获得的数据都是随时间离散的,求取微分方程(13)的解析解比较困难,故在进行数据处理之前,需要将(13)式化为以qj为状态变量的状态方程组,然后进行编程并进行离散化数值仿真。本文仿真程序使用ODE45求解器来求取微分方程的数值解。ODE45表示采用四阶、五阶Runge-Kutta单步算法,算法的截断误差为(Δx)3。

本文研究的关注点在于分离体的姿态角度和姿态角速度信息,以广义坐标(q4,q5,q6)为例重点分析(13)式的姿态变化规律。多体分离过程中,作用在飞行器头部分离体的气动力矩随分离时间变化的实验值如图2所示,为仿真提供了数据输入。上方的实线表示分离过程中作用在分离体上的俯仰力矩,下方虚线表示偏航力矩的值。

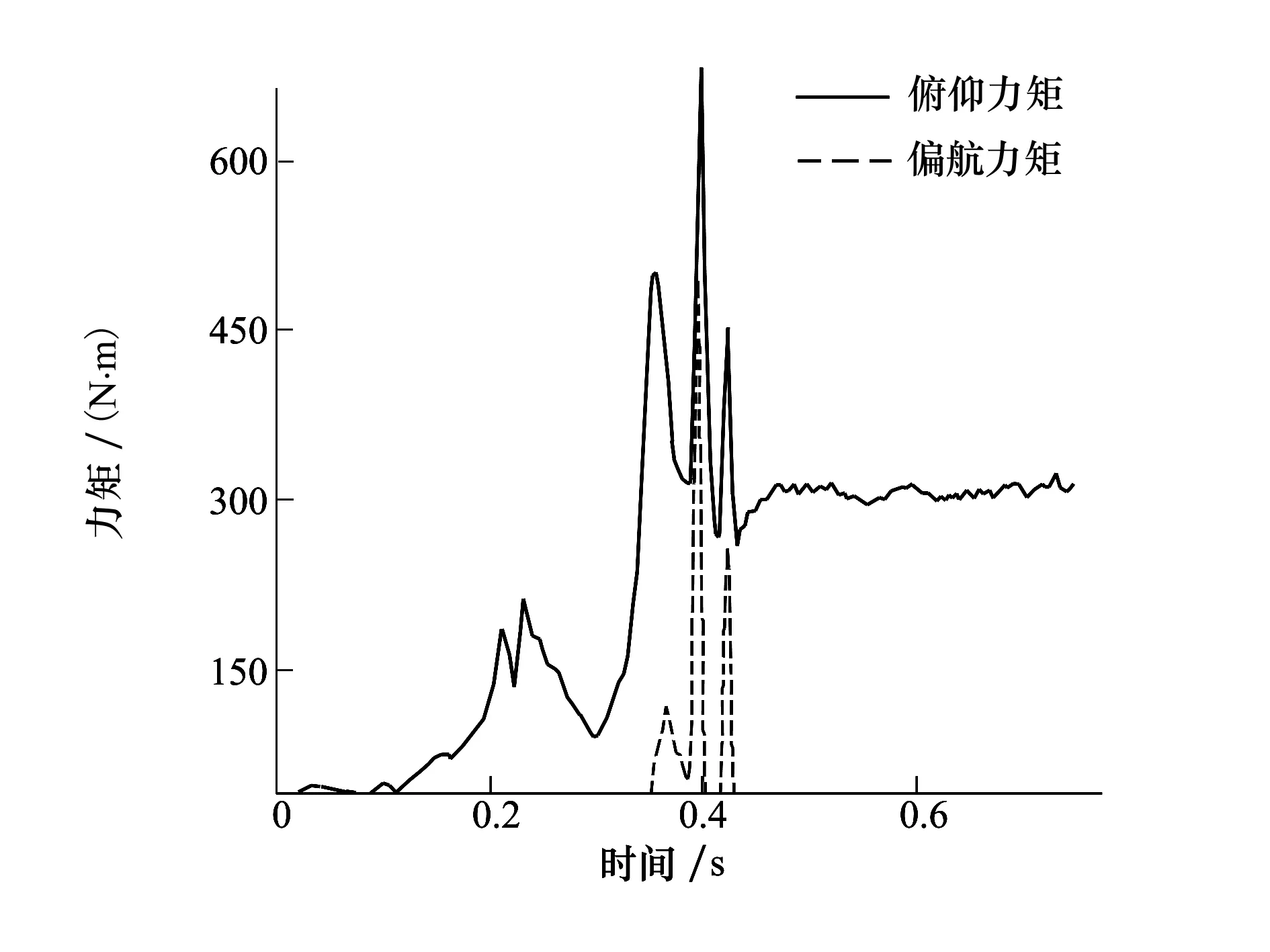
图2 分离过程中作用在分离体上的气动力矩

编写仿真程序带入上述实验数据,并设定仿真步长为1 ms,对待求的微分方程组进行迭代求解。最终得到的结果包含了分离过程中分离体的姿态信息。(13)式的位置广义坐标(q1,q2,q3)分析方法与此类似,是以气动力数据为输入的,其仿真从略。

4.2 仿真及结果分析

设定在每个仿真步长内,分离过程的力矩值为连续变化值,在单个仿真步长内不存在力矩的突变。采用ODE45编写仿真计算程序。姿态角相关的广义坐标(q4,q5,q6)初值均设为0,对分离体在气动力矩作用下姿态角度及角速度的求解进行仿真。具体仿真结果如图3和图4所示。

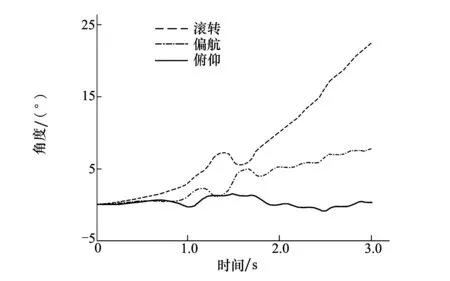
图3 惯性系下姿态角变化曲线

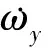
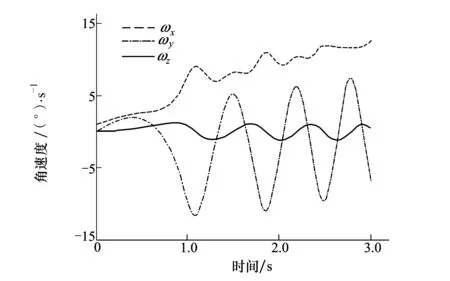
图4 机体坐标系下角速度变化曲线

5 结 论

对于飞行器多体分离过程中有效载荷分离体的运动过程,本文采用拉格朗日力学方法进行分析,选取了广义坐标,建立了分离体的姿态动力学方程,探索了分离体姿态动力学方程组的数值求解方法。本文对推导得出的分离体姿态动力学模型进行了编程仿真,获得了惯性系下姿态角和机体坐标系下角速度的数值仿真结果。最后总结了分离体姿态角及角速度参数的变化规律,为相关的多体分离系统设计提供了参考。

参考文献：

[1] 张科南,李鹏飞,陈万春,吴颂平. 某飞行器级间分离气动力/约束力/飞力综合建模与仿真[J]. 系统仿真学报, 2012, 24(10): 2227-2232

Zhang Kenan, Li Pengfei, Chen Wanchun, Wu Songping. Modeling and Simulation Coupled Aerodynamics, Constraint Force and Flight Dynamics for Stage Separation of Aircraft[J]. Journal of System Simulation, 2012, 24(10): 2227-2232 (in Chinese)

[2] Vera V A. On the Dynamics of a Gyrostat on Lagrangian Equilibria in the Three Body Problem[J]. Multibody Syst Dyn, 2010, 23: 263-291

[3] 张军,张尚强,刘志林. 多星发射上面级的姿态解耦控制[J]. 电机与控制学报,2009, 13(1):40-43

Zhang Jun, Zhang Shangqiang, Liu Zhilin. Decoupling Attitude Control of Upper Stage[J]. Electric Machines and Control, 2009, 13(1): 40-43 (in Chinese)

[4] 洪嘉振. 计算多体系统动力学[M]. 北京:高等教育出版社,1999

Hong Jiazhen. Computational Dynamics of Multibody Systems[M]. Beijing: Higher Education Press,1999 (in Chinese)

[5] 郭俊华. 处理两体问题的拉格朗日方法实例分析[J]. 长春师范学院学报, 2013, 32(2):26-28

Guo Junhua．An Analysis of Actual Example to Deal with Two-Particle System by Lagrange Method[J]. Journal of Changchun Normal University, 2013, 32(2): 26-28 (in Chinese)