杨文茵，张德丰，王传胜

(1.佛山科学技术学院计算机系，广东 佛山 528000；2.暨南大学计算机科学系，广东 广州 510000)

本文将模糊逻辑和神经网络相结合，利用神经网络实现模糊化、模糊规则表达、模糊逻辑推理和反模糊化过程，提出了自适应学习方法，克服了基于先验知识确定模糊规则及网络结构的困难[1]。模糊逻辑、神经网络和模糊神经网络是智能计算这门交叉科学的基本内容，近年来他们都得到了飞速的发展并获得了广泛的应用。多学科算法的相互交叉、相互渗透可以进一步促进现代科学技术的发展[2]。

1 RBF神经网络的学习算法

1.1 模糊神经网络的结构

D-FNN(动态模糊神经网络)的结构是基于扩展的RBF(径向基)神经网络。RBF神经网络具有单隐层的三层前馈网络，RBF结构如图1所示。由于它模拟人脑中局部调整、相互覆盖接收域的神经网络，RBF网络是一种局部逼近网络，已经证明它能以任意精度逼近任一连续函数[3]。

设网络输入n维向量u，输出m维向量y，输入/输出样本对长度为L。

RBF网络隐层第i个节点的输出为

qi=R(‖u-ci‖)

(1)

式中：

u为n维输入向量；ci为第i个隐节点的中心，i=1,2,…,s；‖·‖通常为欧氏范数；R(·)为RBF函数，具有局部感受的特性。它有多种形式，体现了RBF网络非线性映射能力[4]。

网络输出层第k个节点的输出为隐节点输出的线性组合，即

(2)

式中，wk i为qi→yk的连接权；θk为第k个输出节点的阈值[5]。

图1 RBF网络结构

设有p组输入/输出样本up/dd，p=1,2,…,L定义目标函数(L2范数)为

(3)

学习的目的是使

J≤ε

(4)

式中，yp是在up输入下网络的输出向量[6]。

高斯径向基函数网络隐节点的输出为

(5)

式中，[·]表示向量u与ci间的马氏距离。

当∑i为对角阵时，式(5)为

(6)

当∑i为单位阵时，式(5)为

(7)

作用函数是高斯径向基函数(RBF)，是非线性的，即

R(h)=exp(-h)

(8)

(9)

式中，u为n维输入向量，j=1～n；ci为第i个隐节点的中心；σi为第i个隐节点的标准化参数；σij为第i个隐节点第j分量的标准化参数。RBF神经网络被广泛用于函数逼近以及模式识别中，在这些应用中，样本的维数通常很小[7]。正如Moody和Darken在文献[8]中所指出的，“RBF神经网络是最合适用于学习逼近连续的或分段连续的实值映射，其中该映射的输入维数充分的小”。

本文提出了一种动态模糊神经网络D-FNN结构及其学习算法，该模糊神经网络的结构基于扩展的径向基神经网络。其学习算法的最大特点是参数的调整和结构的辨识同时进行，且学习速度快，可用于实时建模与控制。动态模糊神经网络的结构如图2所示，共5层。在图2中，x1,x2,…,xr是输入的语言变量，y是系统的输出，MFij是第i个输入变量的第j个隶属函数，Rj表示第j条模糊规则，Nj是第j个归一化节点，wj是第j个规则的结果参数或者连接权，u指系统总的规则数。

图2 D-FNN结构

1.2 神经网络用于系统辨识

如果实际系统的输出只是依赖于其当前时刻的输入，而与历史输入无关，就称这个系统是静态系统。如果系统的输出不仅依赖于以前的输出而且依赖于当前的输入，则称这类系统为动态系统。n阶动态系统通常可以用如下方程描述[9]：

y(t)=f[y(n)(t),…,y′(t),x(t)]

(10)

其中，y(t)和x(t)分别为对象的输出和输入信号，y(n)(t)为y(t)的n阶微分，它是y(t)的以前信息。如果函数f(·)非线性的，则系统(10)称为非线性动态系统。本文将研究这一类型的系统。

文献[10]指出，在较弱的假设下，任何一个非线性离散时间系统都可用如下的NARMAX(Nonlinear AutoRegressive Moving Average with eXogenous inputs)模型来描述：

y(t)=f[y(t-1),…,y(t-ny),x(t-1),…,

x(t-nx),e(t-1),…,e(t-ne)]+e(t)

(11)

其中y(t)、x(t)、e(t)分别是系统的输出、系统的输入和噪声，f是待辨识的未知函数，ny、nx、ne分别是输出、输入和噪声的最大延迟，e(t)是独立的零均值序列。作为NARMAX的一个特例，实际中经常用到如下的NARX(Nonlinear AutoRegressive with eXogenous inputs)模型：

y(t)=f[y(t-1),…,y(t-ny),

x(t-1),…,x(t-nx)]+e(t)

(12)

基于NARX模型，文献[9]对此作了进一步简化，并提出如下几个没有干扰情况下的模型。

模型Ⅰ

(13)

模型Ⅱ

(14)

模型Ⅲ

y(t)=f[y(t-1),…,y(t-ny)]+

g[x(t-1),…,x(t-nx)]

(15)

基于上述模型，文献[9]提出了如何利用神经网络来进行系统辨识。

用神经网络来进行系统辨识，一个显而易见的方法就是使神经网络或模糊神经网络的输入-输出结构选择和被辨识的系统一模一样。在实际操作上，可以有如下两种模型。

1)并行模型

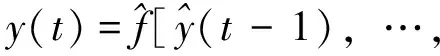
(16)

2)串-并行模型

y(t-ny),x(t-1),…,x(t-nx)]

(17)

2 实验结果与分析

被辨识的对象描述如下：

(18)

这个模型广为研究人员使用，比如，文献[11]和文献[12]，该对象给出的无外力系统的平衡状态分别为(0,0)和(2，2)。如果串-并行辨识模型用来辨识该对象，则这个模型可以用如下方程来表示：

其中，f是三输入单输出的D-FNN。使用同文献[13]和文献[14]相同的输入u(t)=sin(2πt/25)，其结果如图3所示。其中图3(a)表示产生的模糊规则，图3(b)表示训练时的实际输出误差，图3(c)表示均方根误差。与文献[11]、文献[12]及文献[13]结果比较如表1所示。

由表1可以看到，要达到相同的训练误差，只有结构自适应的OLS方法需要65条规则，远大于D-FNN所需要的规则数。文献[11]和文献[12]也采用了修剪计算[15]，其所用的规则数虽然比OLS方法少，但还是比D-FNN的方法多多了，而且训练误差比D-FNN大得多。由图3(d)可以看到，尽管D-FNN的结构很小，但其泛化能力很强。结果表明：与其它算法相比，D-FNN无论在结构上还是性能上都具有明显的优势。

图3 非动态线性系统的辨识

表1 不同算法的性能和结构比较

Table 1 Comparison of performance and structure with different algorithms

D⁃FNNOLS[13]RBF⁃AFS[11]FNS[12]规则数7653522参数数4732628084均方根误差0 02820 02880 1384未列出

为了检验D-FNN的泛化能力，设p=6，n=500。其中p为前6步预测结果，n为500个样本对。选择不同参数，将得到两种不同的神经网络结构，其训练和测试结构列于表2中。

表2 n=500,p=6时训练数据的仿真结构

当p等于6，模糊规则数为10时，图4说明了D-FNN泛化性的测试，其中，前500个点用于训练，后500个点用于预测。由图4及表2可以看出，无论是采样5条规则还是10条规范，所构建的模糊神经网络都具有很强的泛化能力，因为测试误差几乎等同训练误差[16]。表3列出了D-FNN与ANFIS(基于自适应神经网络的模糊推理系统)、OLS(正交最小二乘网络)和RBF-AFS(径向基自适应模糊系统)的比较结果。

图4 D-FNN预测的测试结果

表3不同的结构和性能比较(训练条件：n=500,p=6)

Table 3 Structure and performance comparision(Training condition:n=500,p=6)

方法规则数参数的数量训练的均方根误差测试的均方根误差D⁃FNN101000 00820 0083ANFIS161040 00160 0015OLS352110 00870 0089RBF⁃AFS212100 01070 0128

比较结果显示，即使D-FNN有更多的可调参数，它的性能也并没有ANFIS好。原因是ANFIS通过迭代学习的方式训练，从而可以达到整体的最优解。而D-FNN只能获得次优的结果。然而，与RAN、RANEKF及M-RAN(它们也只能得到次优解)相比，D-FNN结构小而泛化能力更强。

3 结 论

D-FNN算法中，非线性参数是由训练样本和启发方法直接决定的，而没有用优化算法来确定，虽然高斯宽度在学习时可以自适应地调整，但学习规则却很简单。D-FNN算法中，由于分级学习策略的使用可以缓解学习过程中的震荡问题；修剪技术的应用，使得网络的结构不会持续增长。为检验D-FNN的有效性，把D-FNN与其它的学习算法进行了比较，并深入探讨这些算法与其它算法的相互关系，研究表明D-FNN具有简洁的结构和优良的性能。

参考文献：

[1]JANG J-S R.ANFIS:Adaptive-network-based fuzzy inference system[J].IEEE Transactions on Systems,Man,and Cybernetics ,2013,23(3):665-684.

[2]KADIRKAMANATHAN V,NIRANJAN M.A function estimation approach to sequential learning with neural networks[J].neural computation,2012，16(4):954-975.

[3]HONG Z Q.Algebraic feature extraction of image for recognition[J].Pattern Recognition,2011,24(3):211-219.

[4]徐丽娜.神经网络控制[M].北京:电子工业出版社,2009.

[5]WU S Q,ER M J.Dynamic fuzzy neural networks:a novel approach to function approximation[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B,2000,30(2):358-364.

[6]ER M J.WU S Q.A fast learning algorithm for parsimonious fuzzy neural systems[J].Fuzzy Sets and Systems,2002,126:337-351.

[7]任爱红.模糊随机过程函数列均方差一致Henstock积分的可积性[J].中山大学学报:自然科学版,2010,51(4):41-44.

[8]MOODY J,DARKEN C J.fast leaning in network of locally-tuned processing units[J].Neural Computation,2009,1:281-294.

[9]NARENDRA K S,PARTHASARATHY K.Identification and control of dynamical system using neural networks[J].IEEE Transactions on Neural Networks,1990,1(1) :4-27.

[10]LEONTARITIS I J,BILLINGS S A.Input-output parametric models for nonlinear systems,part 1:deterministic nonlinear systems[J].International Journal of Control,2006,41(2):303-344.

[11]CHO K B,CHEN B H.Radial basic fuction based adaptive fuzzy systems and their applications to system identification and prediction[J].Fuzzy Sets and Systems,2006,83(3):325-339.

[12]CHAO C T,CHEN Y J,TENG C C.Simplification of fuzzy neural systems using similarity analysis[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2008,26(2):344-354.

[13]CHEN S,COWAN C N,GRANT P M.Orthogonal least squares learning algorithm for radial basis function network[J].IEEE Transactions on Neural Networks,2009,2(2):302-309.

[14]何正风,张德丰,孙亚民.高斯激活函数特征值分解修剪技术的D-FNN算法研究[J].中山大学学报:自然科学版,2013,52(1):34-39.

[15]伍世虔,徐军.动态模糊神经网络：设计与应用[M].北京：清华大学出版社,2008.