刘素娟，卿光辉

（中国民航大学航空工程学院，天津 300300）

改进后的动力学方程精细积分法

刘素娟，卿光辉

（中国民航大学航空工程学院，天津 300300）

对于结构动力学方程，在分块增维精细积分法的基础上，使各个子块产生共同项，即子块相似化。这样精细积分每次循环的结果，多个子块可以同时利用，同时也减少了计算量和存储量。在非齐次项的处理问题上，取每个步长的中间值，简化了计算，也保留了精度。数值例题显示研究方法的高效性和可行性。

动力学方程；增维分块；精细积分法；子块矩阵；相似化

精细积分问世以来，结构动力学方程求解的过程大为简化。Moler and Van Loan[1]提到了十九种计算方法，并就多种方法的稳定性、适应性和计算精度等问题作了较详细的分析和讨论。钟万勰院士等人提出的精细积分法[2]，在应用于求解线性定常结构动力方程时，能够在数值上得到逼近于机器精度的结果，在相关领域[3～6]得到了广泛应用。而对于非齐次的结构动力方程，顾元宪、陈飚松、张洪武等人提出的增维精细积分法[7]避免了矩阵求逆，同时提高了数值计算的稳定性。但是增维精细积分方法一般要求每一个时间步都要重新通过20次矩阵加、乘迭代来计算T矩阵，所需的计算量和计算时间将很大，特别是在处理大型问题时。张继锋，邓子辰提出的结构动力方程的增维分块精细积分法[9]，在增维精细积分法的基础上，对矩阵进行分块计算，考虑非齐次项的特点，减小了矩阵的维数，实现简化计算，但是在计算速度和非齐次项处理上都不是很理想。张庆云、滕圣刚提出的一种提高增维精细积分法计算精度的方法[10]，在每一个时间步长内，仍然将非齐次项当成常数，但是该常数的值取为该时间段内不同时刻值的平均值，或者取为中间时刻的值，计算精度得到了一定的改善，但是整体计算量的减少并不理想。

本文在前人所做工作的基础上，借鉴已有增维分块精细积分法的思想，对不同子块进行化简处理，使各个子块产生共同项，或者产生每次循环结果项，即子块结构相似化处理。这样不仅可以使相同的项一次性计算，还能使精细积分每次循环的结果，多个子块可以同时利用，同时也减少了计算量和存储量，提高了计算速度。另外，在非齐次项常数化处理时，本文采用最新的张庆云、滕圣刚[10]的非齐次项取值为该时间段内不同时刻值的平均值，或者中间时刻的值，使计算精度大为提高。因而本文在计算速度和计算精度上都有很大的优势，尤其是计算步数较大的问题时优势更加明显。

1 结构动力方程的增维分块精细积分法

1.1 指数矩阵的精细积分法[2]

按常微分方程理论，对于一个齐次方程：

H为定常矩阵，其通解可以表示为:

其中，τ为步长。

精细积分法主要是将注意力放在增量上，而不是全量。假设A为n×n阶矩阵，为了避免舍入误差，利用指数函数的加法定理：

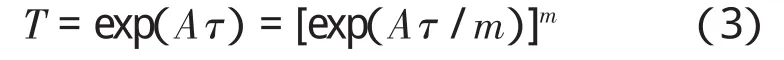
其中，m为任意正整数，且m=2N（例如N=20，则m=1 048 576)。

由于τ是一个小的时间区段，则η=τ/m是一个非常小的时间区段。因此，对于η，有

文献[5]指出指数截断阶数L=4，迭代次数N=20时精细积分法中指数矩阵计算可以认为很接近其精确解答。此时指数矩阵T与单位矩阵In相差不远，因此可写为：

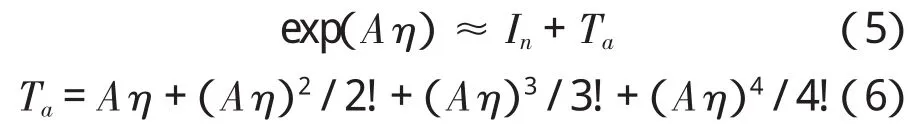
其中，Ta阵是一个小量矩阵。

因为Ta很小，当它与单位阵In相加时，就会成为尾数，在计算机的舍入操作中会被舍去，影响计算精度[8]。所以，至关重要的一点是指数矩阵的存储是式(3)中的 Ta，而不是 Ta+In。

为了计算T，有:

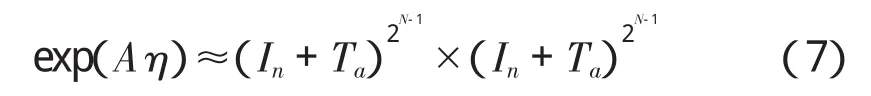
这种分解一直做下去，共N次。其次应注意，对任意矩阵Tb和Tc有:

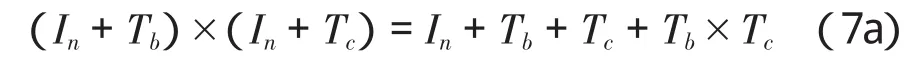
将Tb和Tc都看成为Ta，因此式（4）的 N次乘法在计算机中相当于以下的语句：

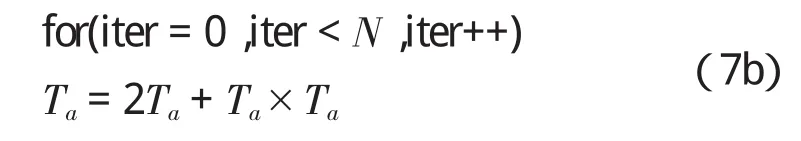
当该语句循环结束后，再执行：

执行N次乘法后，Ta已不再是很小的矩阵了，这个加法已没有严重的舍入误差。

1.2 增维分块精细积分法[7]

一般n维线性定常结构的动力方程可以表示为：

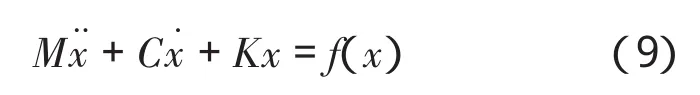
对（9）式进行增维处理可得：

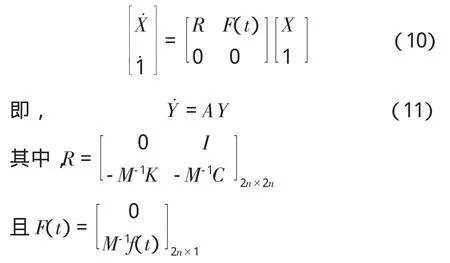
η 为时间步长，在区间[tk，tk+1]内，式（11）可视为常系数微分方程：

再利用迭代求解：

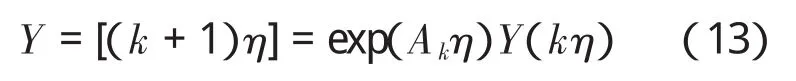
其中，exp（Akη）采用精细积分计算。

2 改进后的动力学方程精细积分方法

对方程（12）进行精细积分，其中N=20，对方程（17）进行精细积分计算时，取N=20，每一个时间步都要重新通过20次矩阵加、乘迭代来计算矩阵,所需的计算量和计算时间将很大。借鉴文献[5]的思想,对矩阵进行分块计算。

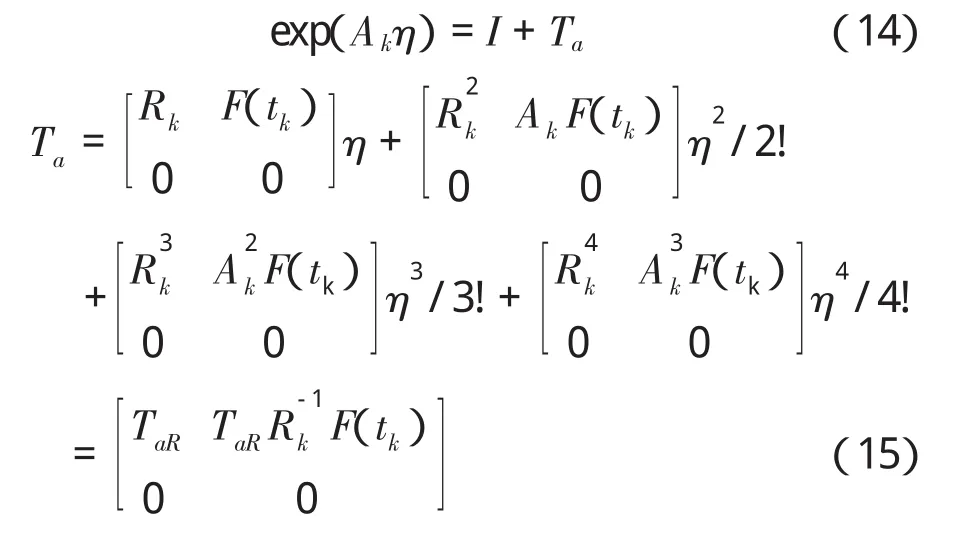
简单检验可知矩阵Rk必为可逆的，其中

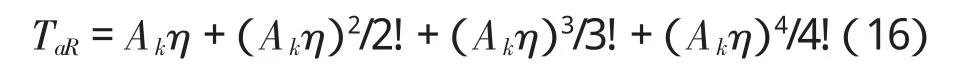
式中的两个子块都含有TaR，相似度很高，这是本文第一次成功的实现了子块的相似处理。

将上式根据（7）式的思想可得出:

联合（18）式和（19）式，可以看出矩阵T的子块T11和 T12中都存在（I+TaR）2i，这使得两个子块存在很高的相似度，这是本文第二次成功的实现了子块的相似化处理。尤其，当T11采用精细积分求解，T11执（7b）式时，T11从第1次到第N-1次，每一次环的结果，刚好可以被子块T12中的（I+TaR）2i项完全利用。根据文献[9]可知：增维后齐次方程的解的迭代表达式为：

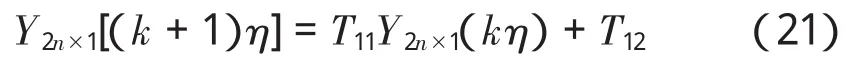
因此，所求线性定常结构的动力学方程的解的迭代表达式为:

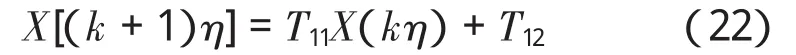
结合以上精细积分的全过程，只要确定初始值，就能很简单的计算出不同步长和不同步数的方程的解。

非齐次项的处理采用文献[10]的方法，将其值取为该时间段内几个不同时刻值的平均值，或者取为中间时刻的值，经过计算分析发现，取中间时刻值满足计算精度的同时，计算量较小。因此，本文取一个时间步长[tk，tk+1]内的中间时刻值，其表达式如下:

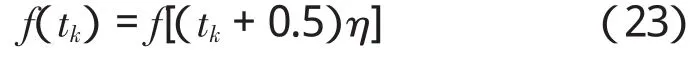
3 实例分析

取自文献[7]，求解的结构动力学方程为：

初始值为：

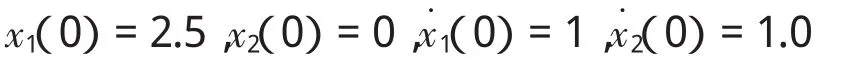
解析解为：

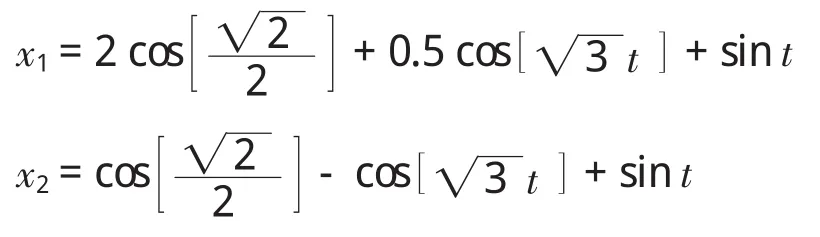
选择步数为1（第1步）的情况，步长由0.01 s增加至0.50 s，每次增加0.01 s，用Mathematica语言编程得到x1，x2的解分别都是50组，并且将其与x1，x2的准确解进行对比，表1将列举出50组数据中的8组数据。

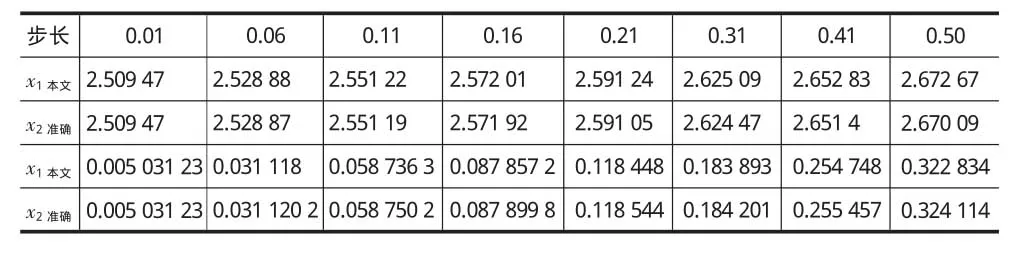
表1 x1，x2新算法的解与准确解其中8组数据的比较

比较分析这8组数据可知，本方方法跟准确值相比，误差很小，即使步长增加至0.50，其结果也能精确至0.01位。再将这50组数据，用Mathematica软件制成图，横轴为变化的步长，纵轴为计算的结果，如图1、图2所示。

据图1和图2显示并分析可知，在步长由0.01增至0.50的整个过程，本文算法x1、x2的解与准确解所代表的每组图形几乎完全重合，再次证明了本文方法的准确性与高精度。

图1 新算法的x1与其准确解比较

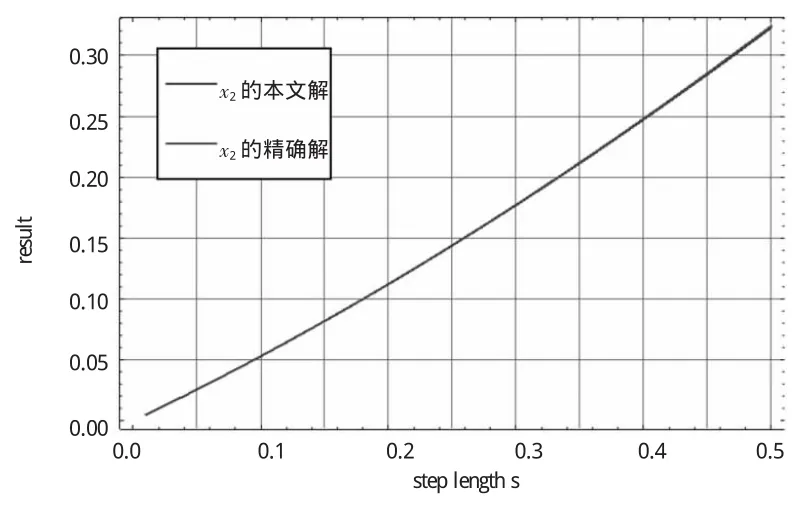
图2 新算法的x2与其准确解比较

在此之前，计算结构动力学方程较快的方法是文[5]的增维分块法，现在将本文方法与文[5]的方法的计算速度进行对比。继续分析上述算例，在步长为0.02的条件下，当步数分别为50 000、100 000、500 000、1 000 000、5 000 000、10 000 000，本文方法与文[5]增维分块法计算时间对比，结果如表2所示。

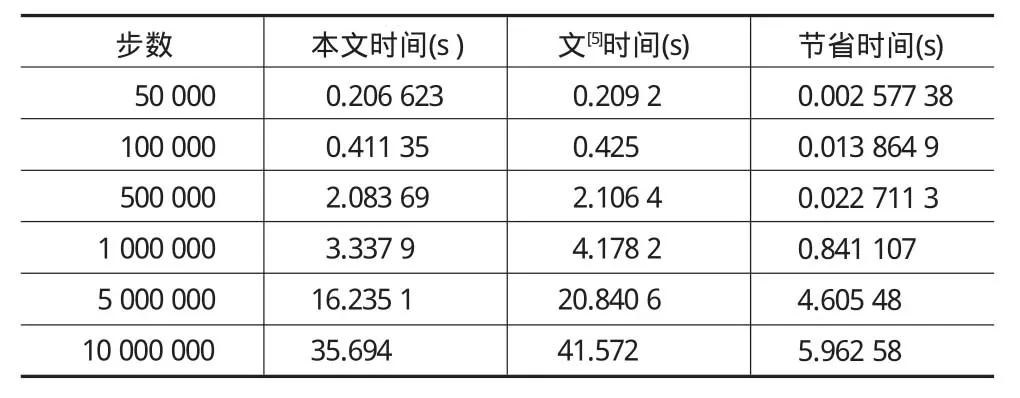
表2 相同步长下，不同步数的时间比较

由表2可以看出，这六组数据中本文方法的时间都比对对应的文[5]的时间要短，当计算的步数增加时，本文方法节省的时间就越多，因此计算的优越性就越明显，这对于解决大步数以及超大步数的结构动力学微分方程是有利的。

4 结束语

本文在增维分块的基础上，结合对子块矩阵使各个子块产生共同项，或者产生每次循环结果项，进行结构相似化处理的核心思想，提出了一种精确快速的，且程序上易实现解决结构动力学问题的快速精细积分方法。在步数很大时，不但能保证计算精度，而且计算速度更快，更能让人满意。

[1]MOLER C,LOAN C V.Nineteen dubiousways to compute the exponentialofamatrix[J].SIAM Rev，1978，20(4):801-836.

[2]钟万勰.结构动力方程的精细时程积分[J].大连理工大学学报，1994，34(2):131-136.

[3]顾元宪，陈飚松.瞬态热传导方程精细积分方法中对称性的利用[J].力学与实践，2000，22(5):19-22.

[4]陈飚松，顾元宪.瞬态热传导方程的子结构精细积分方法[J].应用力学学报，2001，18(1):14-19.

[5]汪梦甫，区达光.精细积分方法的评估与改进[J].计算力学学报，2004，21(6):728-733.

[6]候秀慧，邓子辰，黄立新.桥梁结构移动荷载识别的辛精细积分算法[J].动力学与控制学报，2008，6(1):66-72.

[7]顾元宪，陈飚松，张洪武.结构动力方程的增维精细积分法[J].力学学报，2000，32（4）：447-456.

[8]任 伟，杜铁钧.定常结构动力方程增维精细积分法求解的注记[J].杭州电子科技大学学报，2005，25(1):41-43.

[9]张继锋，邓子辰.结构动力方程的增维分块精细积分法[J].振动与冲击，2008，27(12):88-90.

[10]张庆云，滕圣刚.一种提高增维精细积分法计算精度的方法[J].科学技术与工程，2010，10(31):7627-7630.

The Kinetic Equation of Precise Integration Method Im proved

LIU Su-juan，QINGGuang-hui
(CivilAviation University ofChina College of Aeronautical Engineering，Tianjin 300300，China)

The structure equations,based on the block of increment dimensional precise integration method,so that each sub block into the common items,namely sub blocksimilarity.The precise integration of each cycle results,multiple sub blocks can beused at the same time,butalso reduce the computation and storage.To dealwith problems in nonhomogeneous term,intermediate values of each step,and simplifies the calculation,but also retains the accuracy.Numericalexamples show the efficiency and feasibility of researchmethods.

dynamic equation；incrementdimensionalprecise integrationmethod；block;blockmatrix；similarity

TU311.3

A

1672-545X（2014）04-0004-04

2014-01-07

中国民航大学校级科研基金项目(编号：2012kye07)

刘素娟(1987—)，女，湖北黄冈人，硕士，研究方向：复合材料力学。

book=7,ebook=138