王国勋 王宛山 王 军 舒启林

1.东北大学，沈阳，110819 2.沈阳理工大学，沈阳，110159

0 引言

传统数控系统只支持直线插补和圆弧插补，在加工复杂曲线时，先将曲线用很多段小直线段或圆弧段近似，然后再进行直线插补或圆弧插补，这种方法在高速加工中会带来许多问题：①刀具进给方向快速突变，加速度及加加速度过大，容易导致过冲和振动，从而影响表面质量和加工精度，为了保证表面质量和加工精度，必须降低进给速度［1］；②只针对小线段进行速度规划，在小线段的起点和终点频繁进行加减速，严重影响加工效率，不易实现高速加工；③程序文件庞大，增加了CAD／CAM与CNC之间的数据传输负担。

为了克服传统插补方法的缺点，许多现代CAD／CAM系统开始使用曲线参数描述方法和参数曲线插补技术。非均匀有理B样条曲线（NURBS）由于具有诸多优点而获得广泛应用。另外，NURBS已成为STEP-NC标准中自由曲线曲面唯一的表示形式，即NURBS的应用扩展至CNC领域，CAD／CAM与CNC的数据描述实现了统一。因此，研究直接NURBS插补技术，有利于更有效地利用CAD系统的数据。研究表明，相比直线、圆弧插补技术，直接NURBS插补技术可获得更高的表面质量和效率［2］。

许多研究人员对NURBS插补技术进行了深入的研究。大多数直接插补算法试图用泰勒展开法近似表示进给步长和参数增量之间的关系，Yeh等［3］用一阶泰勒展开式研究了插补算法，提出了自适应插补算法，在保证轮廓误差的前提下根据曲率调节速度；赵国勇等［4］基于二阶泰勒展开式提出了插补算法，以获得更高的精度。但应用泰勒展开式研究插补算法时忽略了高阶项，因此存在累积截断误差，造成实际进给速度与给定速度不一致，存在速度波动。为了解决这个问题，必须对下一插补点的参数值进行误差补偿，Tsai等［5］设计了一种参数曲面曲线“预测-修正”插补器，根据给定的速度误差迭代修正下一插补点参数值，直到满足误差要求为止。此方法能有效地减小速度波动，但是插补过程中需要进行迭代计算，影响插补实时性，如果某次迭代时间超过插补周期，将打乱插补过程。

本文根据插补原理，运用NURBS直接插补思想，研究了NURBS快速直接插补算法。为了满足插补精度的要求，插补速度可根据弓高误差限定值自适应调整。

1 NURBS曲线描述

一条k次NURBS曲线可以表示为一分段有理多项式矢函数［6］：

其中，ωi（i＝0，1，…，n）称为权因子，分别与控制顶点di相联系；Ni，k（u）是k次规范B样条基，由节点矢量U ＝ （u0，u1，…，un＋k＋1）决定，通常由De Boor-Cox递推公式定义。

2 目前的NURBS曲线插补方法

目前大多数NURBS插补方法都是基于泰勒展开式的，即用泰勒展开式近似求取下一插补点的参数值，常用的有一阶泰勒展开式和二阶泰勒展开式。插补计算公式如下。

一阶泰勒展开式：

二阶泰勒展开式：

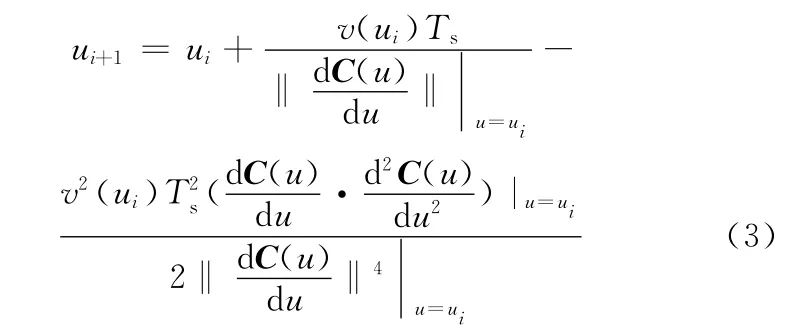
由式（2）、式（3）可发现，泰勒公式展开法插补计算忽略了高阶项，致使进给速度发生变化，增大了弓高误差［7］。如图1所示，下一个插补点参数理论值为ui＋1，对应的弦长为ΔLi，而利用泰勒公式法计算得到的下一插补点参数值为u′i＋1，对应的弦长为ΔL′i，由于u′i＋1＜ui＋1，所以ΔL′i＜ΔLi，而插补周期为定值，所以实际插补进给速度小于给定速度，产生速度波动。另外，计算插补速度时是按照曲线弧长对时间导数求取的，而根据插补原理，刀具实际路径为弦长，而非弧长，如图2所示，插补时刀具实际走过的路径为弦长ΔLi，而不是弧长ΔSi，因此，使用泰勒公式展开法进行插补计算，存在速度波动问题。本文根据插补原理，基于进给速度求取下一插补点插补参数增量Δui来解决这一问题。

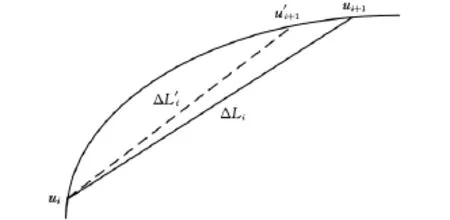
图1 泰勒展开式插补算法

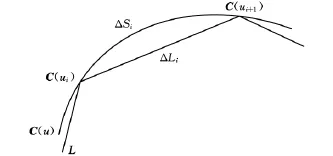
图2 NURBS曲线插补原理图

3 插补算法

3.1 插补计算过程

假设NURBS曲线C（u）在定义域中连续并且二阶可导，曲率半径ρ（u）存在并连续，且曲线上任意插补点满足max｜ΔLi｜≪ρi。根据插补原理，可求得插补计算公式［8］：

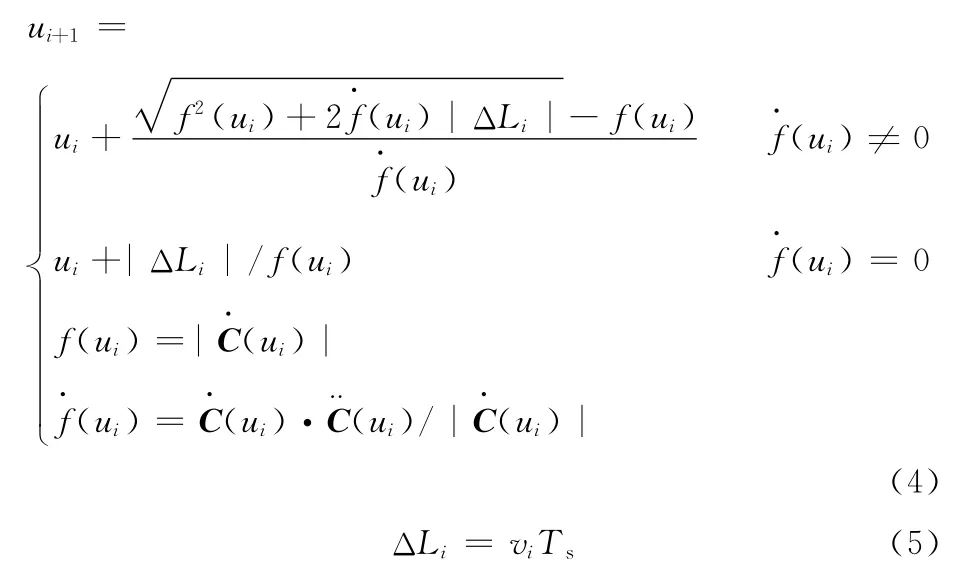
其中，ΔLi为插补弦长（步长），vi为给定进给速度，由式（4）、式（5）可知，下一插补点参数值ui＋1由进给速度vi决定，有效地减小了进给速度的波动。

3.2 特殊点处理

如果k次NURBS曲线内节点重复度为k，则曲线在该点处形成一个尖点，如图3所示。

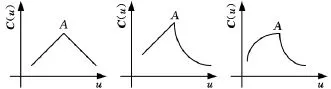
图3 NURBS曲线上的尖点

通常，在尖点区域加速度和加加速度容易超过机床最大允许值，不利于高速、高精度加工，为了解决这个问题，Shen等［9］提出了一种二维NURBS曲线的插补算法，将曲线在尖点处分段，然后在每个分段上进行插补，在加工尖点区域前必须进行减速，在每个尖点处速度都要减到零，下一段曲线插补速度从零开始加速，这样避免了尖点处的加速度和加加速度突变，但却降低了加工效率。又因为曲线在尖点处不存在二阶导数，因此本文的插补算法在尖点处不适用，为了保持整条曲线插补的连续性，提高加工效率，必须对尖点处曲线进行处理。本文将尖点处曲线在允许的误差范围内进行近似插值，使其变光滑，且二阶可导，保持插补的连续性，提高加工效率。具体方法如下。

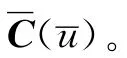
4 NURBS快速计算方法

由以上分析可知，在NURBS插补计算过程中，需要进行NURBS求值、求导的计算。对于NURBS曲线的计算主要是对非均匀B样条基的计算，一般采用de Boor递推算法［10］进行计算，但是每一次计算都要重复算法中的递归调用过程和计算过程，影响效率。对于求导计算，NURBS曲线的定义式（1）是有理分式，对NURBS曲线直接求导非常复杂，分母会出现高次幂，因此，研究NURBS的快速计算法对于插补算法具有重要意义。NURBS曲线是以非均匀B样条为基础的样条曲线，因此可以转换为矩阵表示，与常规表示方法比较，矩阵表示法求值求导效率高。

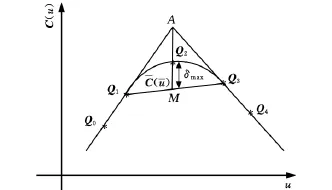
图4 尖点处的NURBS插值

4.1 NURBS快速求值算法

根据B样条基函数性质得到，当u∈ ［ui，ui＋1］时，NURBS曲线可表示成矩阵形式：

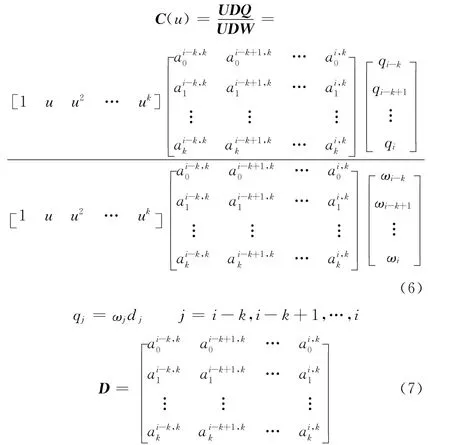
只需求出系数矩阵D，即可计算曲线C（u），因此，研究系数矩阵D的直接递推法对于NURBS的计算具有实际意义。de Boor［11］给出了B样条的导数公式：

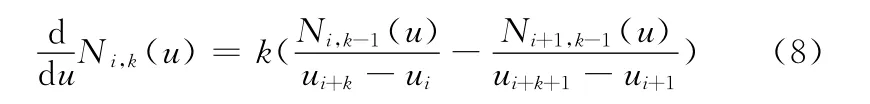
在递推过程中还要满足函数的连续条件：

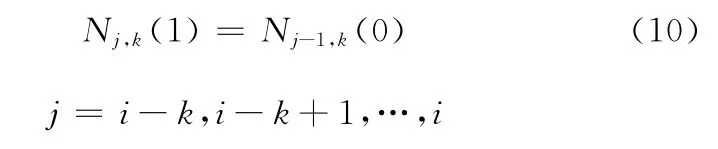
于是，每积分递推式（9）中第二式一次，可得到高一次的非均匀B样条基函数，经过逐次积分便可递推出任意次非均匀B样条基函数。式（9）中第二式左端积分后的结果为Nj，k（u），其多项式表示为

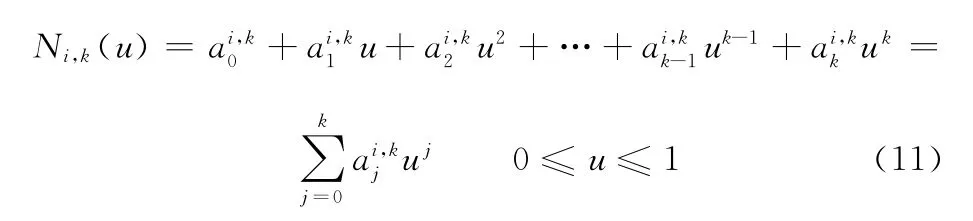
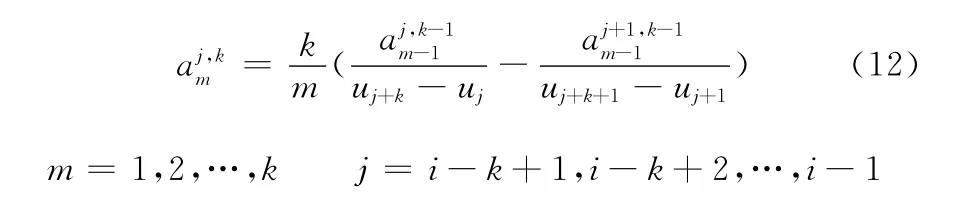
根据非均匀B样条的性质，当u∈ ［ui，ui＋1］时，有

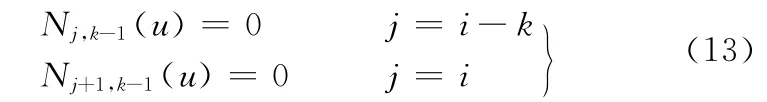
因此

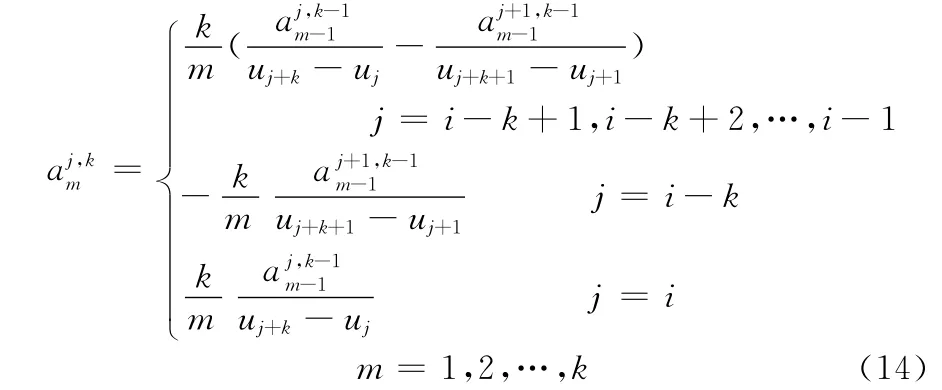
由式（10）得

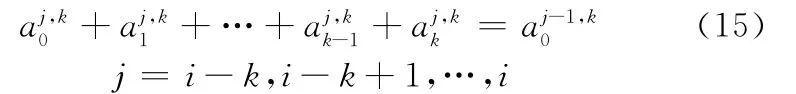
由非均匀B样条的性质，可得j＝i-k时有

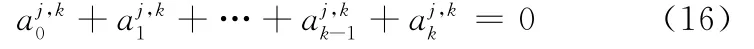
因此得

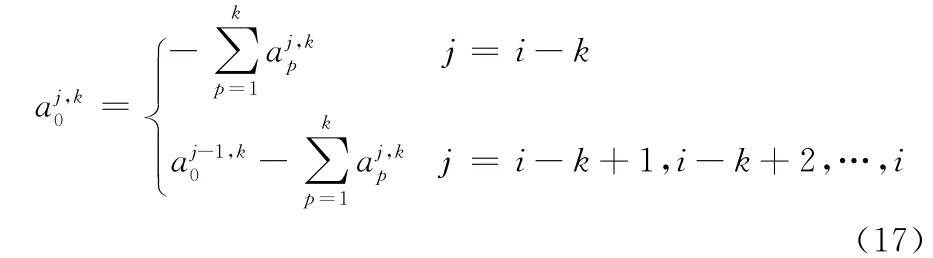
综合式（14）和式（17）可得，系数矩阵D全部元素的递推公式为

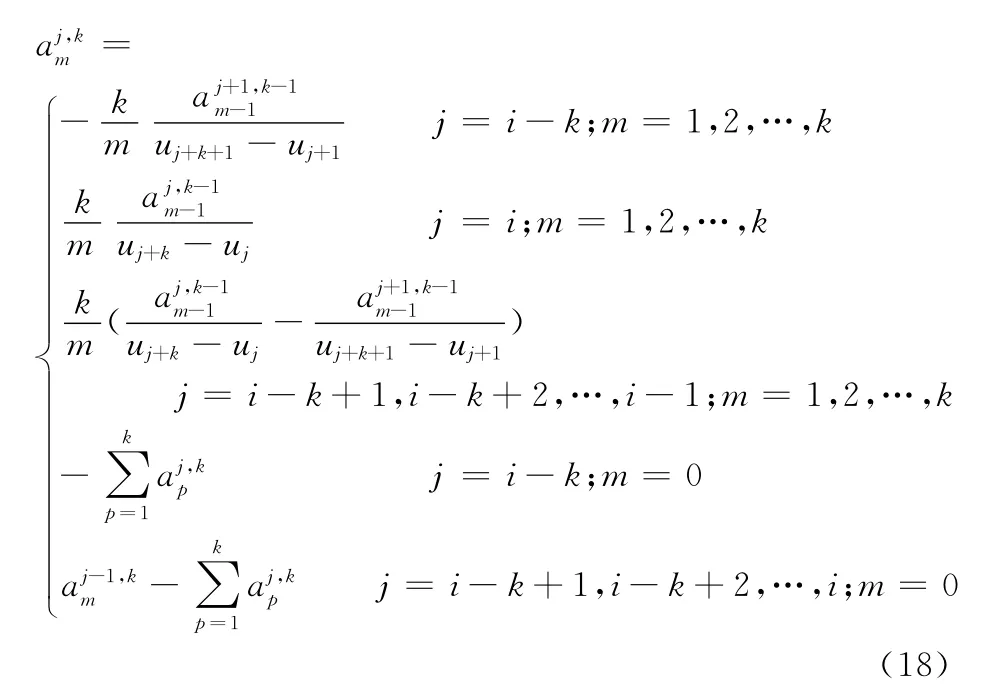
4.2 NURBS快速求导算法

由于NURBS曲线是有理分式形式，求导计算复杂，因此，可将式（1）写成非有理形式：

即

对式（20）两端求r阶导数得

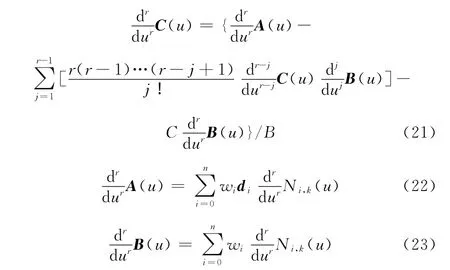
根据文献［6］，Ni，k（u）的r阶导数可由基函数Ni，k-r，Ni＋1，k-r，…，Ni＋r，k-r来计算，即

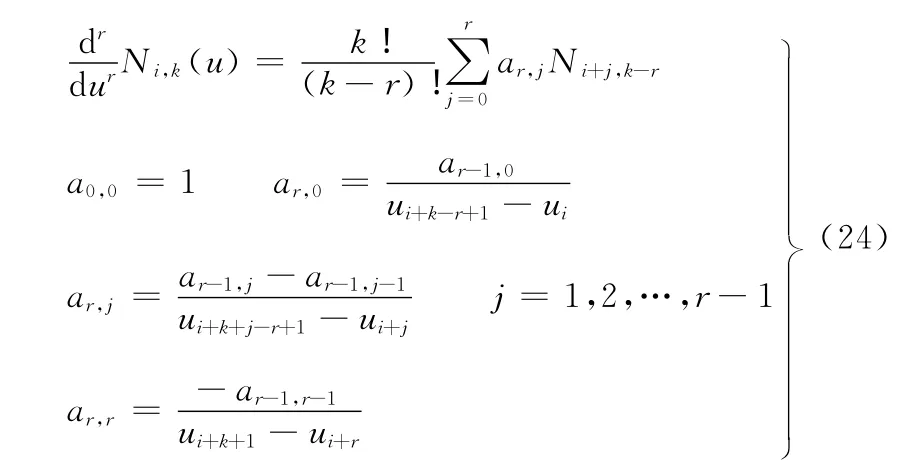
而基函 数 Ni，k-r，Ni＋1，k-r，…，Ni＋r，k-r已 经 在 上 节求值过程中得出，因此可直接调用。可见求导过程不需要递推，只需进行四则运算即可，大大提高了运算效率。

4.3 快速算法效率分析

由以上分析可看出，NURBS的求值求导运算就是对非均匀B样条基函数的运算，因此，本文针对计算NURBS曲线中的非均匀B样条基函数所需计算次数来衡量算法时间复杂度，见表1。

表1 算法复杂度

Tmul、Tadd、Ttotal分别为乘除运算、加减运算、总运算次数。由表1可看出本文方法运算速度比传统的de Boor-Cox方法快一倍多，具有更高的运算效率。

5 插补误差处理

NURBS插补过程中存在两种误差，一种是轨迹误差，一种是弓高误差，如图5所示，εi为轨迹误差，δi为弓高误差。为了达到较高的加工精度，插补过程中必须控制插补误差。由以上分析可知，NURBS插补的每一插补点都在NURBS曲线上，因此不存在轨迹误差，插补过程中误差主要由弓高误差引起，必须对弓高误差进行控制。弓高误差的计算是NURBS插补算法的主要任务之一，直接计算弓高误差，计算复杂，计算量大，且影响插补的实时性，因此可采用近似算法。计算过程如下：以插补点C（ui）处的曲率半径为半径，以插补步长ΔLi为弦长，作圆弧ΔS′i，代替插补曲线弧ΔSi，如图6所示，ρi为曲率半径，δi为弓高误差，可求得弓高误差为

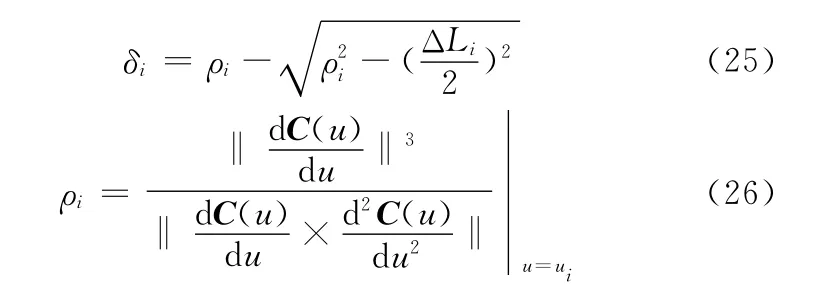
图5 NURBS插补过程中的误差

图6 NURBS插补弓高误差近似描述

由式（5）和式（25）可以看出，弓高误差受进给速度和曲率半径影响，进给速度越大，弓高误差越大；反之，弓高误差越小。在实际加工过程中，总是希望进给速度尽可能保持恒定，以获得尽可能高的表面加工质量，但是，随着曲线曲率的变化，弓高误差可能会超出限定值，为了解决这个问题，本文采用自适应方法规划进给速度，即当误差未超过限定值时，以恒定的进给速度进行插补；当误差超过限定值时，根据插补点的曲率半径自适应调节进给速度。假定弓高误差限定值为δmax，进给速度按下式进行自适应调节［3］：

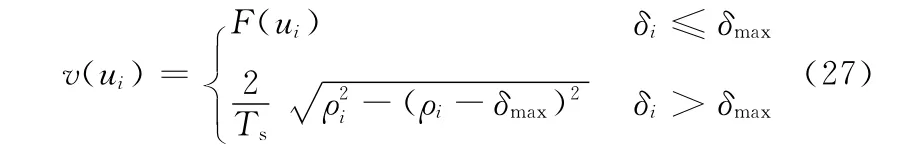
式中，F（ui）为ui处给定的进给速度。

6 仿真分析

为了验证本文方法的可行性和有效性，采用MATLAB进行仿真验证。分别对本文方法、一阶泰勒展开法、二阶泰勒展开法的速度波动率进行仿真，速度波动率按下式计算：

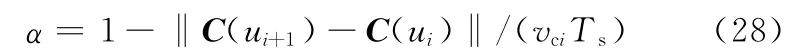
式中，vci为给定的进给速度。

仿真计算机 CPU 频率为2.2GHz，内存2GB。NURBS曲线参数如表2所示，仿真曲线图形如图7所示。

表2 NURBS曲线参数表

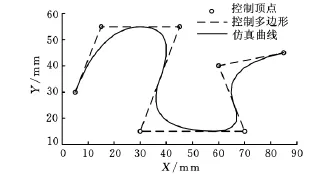
图7 NURBS曲线图

本文方法、一阶泰勒展开法、二阶泰勒展开法的速度波动率仿真图形分别如图8～图10所示。

图8 本文方法速度波动率

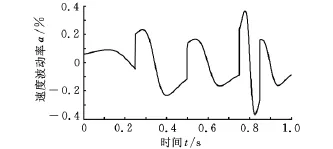
图9 一阶泰勒展开法速度波动率

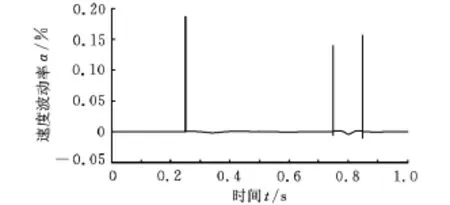
图10 二阶泰勒展开法速度波动率

由图8～图10可得出三种方法的平均速度波动率（表3），可以看出，本文方法的平均速度波动率最小。

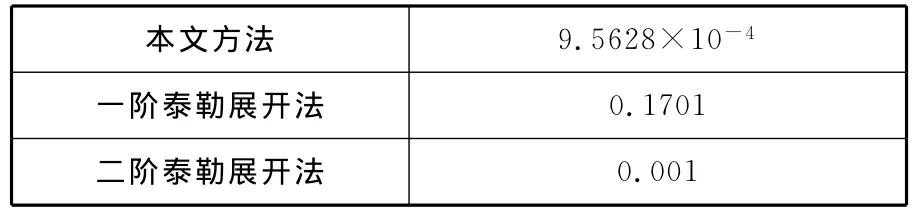
表3 平均速度波动率 %

7 结论

（1）本文方法能够有效地减小速度波动，并保持进给速度的连续性，提高加工效率和表面质量。

（2）推导出NURBS快速求值、求导算法，提高了计算速度和插补实时性。

（3）插补速度随弓高误差限制自适应调节，提高了插补精度。

（4）仿真实例表明，本文方法可行、有效，为高性能NURBS插补器的开发提供了理论基础。

［1］Emami M M，Arezoo B.A Look-ahead Command Generator with Control Over Trajectory and Chord Error for NURBS Curve with Unknown Arc Length［J］.Computer-aided Design，2010，42：625-632.

［2］Wang Junbin，Yau Hong-Tzong.Real-time NURBS Interpolator：Application to Short Linear Segments［J］.Int.J.Adv.Manuf.Technol.，2009，41（11／12）：1169-1185.

［3］Yeh S S，Hsu P L.Adaptive-feedrate Interpolation for Parametric Curves with a Confined Chord Error［J］.Computer-aided Design，2002，34（3）：229-237.

［4］赵国勇，徐志祥，赵福令.高速高精度数控加工中NURBS曲线插补的研究［J］.中国机械工程，2006，17（3）：291-294.Zhao Guoyong，Xu Zhixiang，Zhao Fuling.Study on NURBS Curve Interpolator in the High Speed and High Accuracy CNC Machining［J］.China Mechanical Engineering，2006，17（3）：291-294.

［5］Tsai M C，Cheng C W.A Real-Time Predictor-Corrector Interpolator for CNC Machining［J］.Journal of Manufacturing Science and Engineering，2003，125（3）：449-460.

［6］Piegl L，Tiller W.The NURBS Book［M］.2nd ed.Berlin：Springer，1997.

［7］Yan Cunliang，Du Daoshan，Li Congxin.Design of a Real-time Adaptive Interpolator with Parameter Compensation［J］.Int.J.Adv.Manuf.Technol.，2007，35（1／2）：169-178.

［8］金建新.机床CNC系统中任意空间曲线的可控步长插补方法［J］.机械工程学报，2000，36（4）：95-97.Jin jianxin.Prearranged Step Interpolation Method for Random-space-curve in CNC Machine Tool System［J］.Chinese Journal of Mechanical Engineering，2000，36（4）：95-97.

［9］Shen Hongyao，Fu Jianzhong，Fan Yongqiang.A New Adaptive Interpolation Scheme of NURBS Based on Axis Dynamics［J］.Int.J.Adv.Manuf.Technol.，2011，56（1／4）：215-221.

［10］王田苗，曹宇男，陈友东，等.基于de Boor算法的NURBS曲线插补和自适应速度控制研究［J］.中国机械工程，2007，18（21）：2608-2613.Wang Tianmiao，Cao Yunan，Chen Youdong，et al.NURBS Interpolation and Feedrate Adaptive Control Based on de Boor Algorithm［J］.China Mechanical Engineering，2007，18（21）：2608-2613.

［11］de Boor Carl.A Practical Guide to Splines［M］.New York：Springer-Verlag，2001.