石学军，穆静静，杨 丛

(中国矿业大学理学院，中国 徐州 221116)

考虑下面的反射倒向随机微分方程(简记为RBSDE)：

(1)

所对应的障碍问题.文献[1]在生成元g满足Lipschitz条件下得到了方程的适应解，并说明了此类方程的解与最优停时问题的值函数及偏微分方程障碍问题的联系.随后，文献[2]运用该理论解决了金融市场上的美式期权定价问题.由于RBSDE在经济金融、随机控制等领域的重要应用，它的基本理论及与之相关问题也引起了众多学者的关注.特别地，人们在减弱关于生成元g满足Lipschitz连续条件的存在唯一性及比较定理方面做了很多工作.例如，Matoussi[3]在生成元g关于(y,z)连续、线性增长且g(t,0,0)有界的条件下，证明了极大和极小解的存在性.文献[4]证明了g关于y连续、超线性增长，且关于z连续、平方增长的条件下得到了解的存在性.Xu[5]在生成元g关于y满足单调条件、具有一般增长性，且关于z满足Lipschitz连续的条件下得到了解的存在唯一性.文献[6]在生成元g关于(y,z)广义Lipschitz的条件下，给出了无穷区间的RBSDE存在唯一解的结果.最近，Fan[7]研究了无穷区间的无障碍BSDE，又在一类更弱的条件下获得了解的存在唯一性及比较定理等相关结果.其他研究成果请见文献[8～15].那么，在RBSDE理论中是否也有类似的结论呢？

本文通过BSDE构造惩罚方程列，把BSDE的解不断推向障碍之上而得到相应的RBSDE的解的办法，得到了生成元广义线性增长且关于(y,z)连续的RBSDE解的存在性.其次，在此基础上证明了RBSDE解的比较定理；进一步，可将解的唯一性作为其推论.

1 预备知识

设(Ω,F,P)为一概念空间，T是一个取值有限或无限的广义实值常数.(Bt)t≥0是此空间上的d维标准Brown运动，(Ft)t≥0是该Brown运动生成的完备σ域流：

Ft

其中，N是所得P-可略集全体.

RBSDE的生成元g是一个定义在[0，T]×Ω×R×Rd上的实值函数，并且对任意给定的y,z∈R×Rd,(g(t,ω,y,z))0≤t≤T是一个Ft-循序可测过程；下障碍(Lt)t∈[0,T]是一个连续的Ft-适应过程.如果存在Ft-适应过程形成的三元组(Yt,Zt,Kt)t∈[0,T],其中(Yt,Kt)t∈[0,T]连续且(Kt)t∈[0,T]是初值为0的增过程，使得RBSDE(1)成立，则称此三元组(Yt,Zt,Kt)t∈[0,T]为RBSDE(1)的一个解.

在本文中，我们只讨论如下意义的具有平方可积特征的解.为此引入如下记号：

L2(Ω,FT,P){ξ是FT可测的实值随机变量：E()<+∞};

H2{(φt)t∈[0,T]是Rn值循序可测过程：

P2{(φt)t∈[0,T]是Rn值连续，循序可测过程：

定义1(RBSDE的L2-解) 我们称适应过程构成的三元组(Yt,Zt,Kt)t∈[0,T]为关于终端变量ξ,终端时刻T，生成元g和下障碍L的RBSDE(ξ,T,g,L)的一个L2-解，若它是此方程的解，且满足(Yt,Zt)t∈[0,T]属于空间P2×H2;KT∈L2(Ω,FT,P).

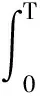
文献[6]在下述的(A1)～(A2)条件下，得到了无穷区间RBSDE的存在唯一性结果.

(A1)生成元关于(y,z)满足广义Lipschitz条件，即dP×dt-a.e.,

∀y1,y2,z1,z2,|g(t,ω,y1,z1)-g(t,ω,y2,z2)|≤u(t)|y1-y2|+v(t)|z1-z2|.

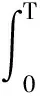
进而，如果BSDE的生成元g满足如下2个假设：

(H1)生成元g关于(y,z)广义线性增长，即

dP×dt-a.e.,∀y,z,|g(t,ω,y,z)|≤ft(ω)+u(t)|y|+v(t)|z|.

(H2)生成元g关于(y,z)连续，即dP×dt-a.e.,g(t,ω,·,·):R×Rd→R为一个连续函数.

注2这是文献[9]结果的无穷时间区间的版本，其证明与有限时间区间相仿.

进一步，记H{φ(t)|φ(·):R+→R+为确定性非减函数且φ(0)=0},若生成元g满足如下条件：

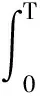
则在BSDE中，亦会有比较定理成立；从而结合前面的存在性条件易知这样的BSDE存在唯一解.

本文的主要结果就是在生成元满足(H1)～(H2)，(H3)～(H4)的条件下，分别得到了RBSDE的解的存在性、比较定理和唯一性定理.

2 主要结果

2.1 存在性

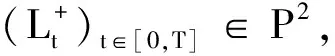
(2)

的一个极小L2-解，并定义

(3)

取α(s)=2u(s)+2v2(s),对(3)式两边取期望，则

(4)

对(3)式两边分别取sup和期望运算，令C为一变动常数(下文亦然)并用Davis-Burkholder-Gundy不等式，可知

(5)

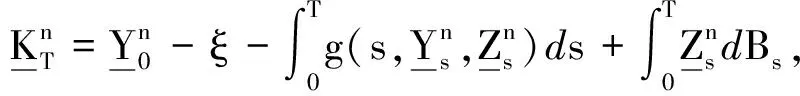
(6)

结合式(4)～(6)可得

(7)

则由(4)，(5)，(7)式可得

(8)

由于

(9)

结合(7)～(9)可得∀n∈N*,

则引理2得证.

令τ是一个满足0≤τ≤T的停时，那么

通过分部积分公式和Lebesgue控制收敛定理，易得

由于生成元满足假设(H1),我们可得

且

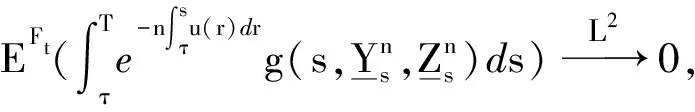
(10)

注意到随机积分部分为一致可积鞅，因此

(11)

由引理2和3可知，(11)式右边第2，3项收敛到0.对于第1项，由于生成元g满足(H1)，由Hölder不等式，引理2，可得

再由基本不等式2yz≤εy2+1/εz2(ε>0取值待定)，并结合Davis-Burkholder-Gundy不等式可知

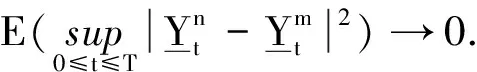
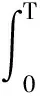
对方程(2)两边取极限，则可知(Yt，Zt，Kt)t∈[0,T]是方程RBSDE的解.

2.2 比较定理与唯一性

按文献[7]证明BSDE解的比较定理的办法，可以得到如下RBSDE的比较定理.

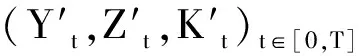
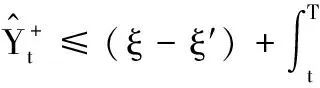
注3对生成元假设条件(H3)中的函数ρ(·)的凹性假设可去掉.

通过前述结果并验证生成元g的条件，可以得到如下结果.

从定理1的证明可知

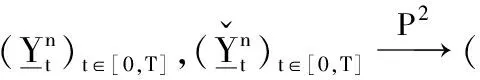
另外，由无障碍BSDE的极小解比较定理(引理1)可知

参考文献：

[1] KAROUI N, KAPOUDJIAN C, PARDOUX E,etal. Reflected solutions of backward SDE’s and related obstacle problems for PDE’s[J]. Ann Probab, 1997,25(2):702-737.

[2] KAROUI N, PARDOUX E, QUENEZ M. Reflected backward SDE’s and American options[C]//ROGERS L C G, TALAY D. Numerical method in finance[M]. Cambridge: Cambridge University Press, 1997:215-231.

[3] MATOUSSI A. Reflected solutions of backward stochastic differential equations with continuous coefficient[J]. Statist Probab Lett, 1997,34(4):347-354.

[4] KOBYLANSKI M, LEPELTIER J P, QUENEZ M C,etal. Reflected BSDE with superlinear quadratic coefficient[J]. Probab Math Statist, 2002,22(1):51-83.

[5] XU M Y. Backward stochastic differential equations with reflection and weak assumptions on the coefficients[J]. Stoch Proc Appl, 2008,118(6):968-980.

[6] HAMADENEN S, LEPELTIER J P, WU Z. Innite horizon reflected backward stochastic dirential equations and apllications in mixed control and game problems[J]. Probab Math Statist, 1999,19(2):211-234.

[7] FAN S, JIANG L, TIAN D J. One-dimensional BSDEs with nite and innite time horizons[J]. Stoch Proc Appl, 2011,121(3):427-440.

[8] CHEN Z, WANG B. Innite time interval BSDEs and the convergence ofg-martingale[J].J Austral Math Soc, 2000,69(2):187-211.

[9] LIU J, REN J. Comparison theorem for solutions of backward stochastic dierential equations with continuous coefficient[J]. Statist Probab Lett, 2002,56(1):93-100.

[10] KOBYLANSKI M. Backward stochastic dierential equations and partial dierential equations with quadratic growth[J]. Ann Probab, 2000,28(2):558-602.

[11] BRIAND P, COQUET F, HU Y,etal. A converse comparison theorem for BSDE and related properties ofg-expectation[J]. Electron Comm Probab, 2000,5:101-117.

[12] BENDER C, KOHLMANN M. BSDEs with stochastic Lipschitz condition[EB/OL]. 2000, http://cofe.uni-konstanz.de/Papers/dp00-08.pdf.

[13] LÜ W. Reflected BSDE with stochastic Lipschitz coefficient[EB/OL]. 2009, arXiv: 0912.2162v3 [math. PR].

[14] HAMADENE S, LEPELTIER J P, MATOUSSI A. Double barrier reflected backward SDE’s with continuous coefficient[EB/OL]. 1997, http://perso.univ-lemans.fr/～amatou/HLMBSDE-97.pdf.

[15] CHEN S.Lpsolutions of one-dimensional backward stochastic dierential equations with continuous coefficients[J]. Stoch Anal Appl, 2010,28(5):820-841.