从高考三角问题看正弦、余弦定理的辩证统一
2013-10-27孙郁娥吕峰波
●孙郁娥 ●吕峰波
(嘉兴市秀州中学 浙江嘉兴 314033) (嘉兴市第一中学 浙江嘉兴 314000)
从高考三角问题看正弦、余弦定理的辩证统一
●孙郁娥 ●吕峰波
(嘉兴市秀州中学 浙江嘉兴 314033) (嘉兴市第一中学 浙江嘉兴 314000)
解三角形是高考中的常见试题,纵观2012年全国各地的高考数学卷,其中不乏各类解三角形的题,归纳起来有以下4种类型:
(1)已知两角和任一边,解三角形;
(2)已知两边和其中一边的对角,解三角形;
(3)已知两边及其夹角,解三角形;
(4)已知三边,解三角形.
事实上,这4类解三角形问题在教科书上已给出了明确的解法,而且很多教学参考书上把它们的解法归纳为:利用正弦定理可以解决类型(1)和类型(2);利用余弦定理可以解决类型(3)和类型(4).笔者发现这样的归纳很容易把学生带入一个误区,学生会认为类型(1)和类型(2)必须用正弦定理来做,而类型(3)和类型(4)则只能用余弦定理去解决.
而正弦、余弦定理作为揭示一般三角形边角关系的重要定理,它们之间不是相互独立的,而是辩证统一的关系.从证明方法上看,两者可以有各自独立的证明方法,也可以互推,因此用正弦定理能解的三角形,用余弦定理也可以解,反之亦然,只是不同的方法计算繁简不一.下面笔者以2012年的数学高考题为例,来阐述这一问题.
1 已知两角和任一边,解三角形
例1

( )

(2012年广东省数学高考文科试题)

而事实上,设角A,B,C所对的边分别为a,b,c,也可以用余弦定理得
将a,A,B的值代入解方程组即可得到b,c,C.只是这个方程组解起来有点麻烦,尝试后有意外发现.3个式相加得
0=a2+b2+c2-2bccosA-2accosB-2abcosC,
即 0=a2cos2B+b2cos2A+c2-2bccosA-2accosB+
2abcosBcosA+a2sin2B+b2sin2A-2abcosBcosA+
2abcos(A+B),
亦即0=(acosB+bcosA-c)2+(asinB-bsinA)2,
因此
asinB=bsinA,c=acosB+bcosA,
即csinB=acosBsinB+bcosAsinB=
bsinAcosB+bcosAsinB=bsinC,

评注由此可见,已知两角和任一边时,用正弦定理求解比用余弦定理求解在计算上更简单,因此我们常说用正弦定理解决此类问题.而用余弦定理去求解也是可行的,只不过求解方程组的过程要复杂一些,但最后殊途同归.
2 已知两边和其中一边的对角,解三角形
例2

(2012年北京市数学高考文科试题)

而事实上,也可以用余弦定理
a2=b2+c2-2bccosA,
将a,b,A的值代入整理,得

解得


但此处涉及到一个问题就是所得的一元二次方程的根可以有2个,2个根是否都满足条件呢?如果有增根,又该如何取舍?笔者经过仔细推敲,发现只要是正根,必定均满足条件,无需检验能否构成三角形.简单证明如下:
由余弦定理知
a2=b2+c2-2bccosA,
将a,b,A的值代入整理得关于c的一元二次方程
c2-(2bcosA)c+(b2-a2)=0,
从而
Δ=(-2bcosA)2-4(b2-a2)=4(a2-b2sin2A).

同理,当A为锐角时,分a
评注由此可见,类型(2)也是2个定理均可以用.一般来说,求角用正弦定理更快捷,若求第三边,则用余弦定理只需解一个方程即可完成,比用正弦定理更直接.
3 已知两边及其夹角,解三角形
例3

(2012年重庆市数学高考文科试题)
分析此题一般考虑先用余弦定理求出边


若不是特殊三角形,则可用余弦定理求出cosB,再求sinB,也可以先求sinC,再用正弦定理求出sinB.不管用哪一种方法,这里都要先用余弦定理求出第三边c.
同样来思考一个问题,可不可以先用正弦定理来计算呢?

化简得
bsinBcosC+bcosBsinC=asinB,
即

解得

于是

评注由此可见,类型(3)也是既可以用余弦定理也可以用正弦定理来解决.我们发现先用正弦定理计算相对复杂,因此大多数教学参考书上常将此类问题归纳为用余弦定理可以解决的问题.
4 已知三边,解三角形
例4如图1,正方形ABCD的边长为1,延长BA至E,使AE=1.联结EC,ED,则
( )

(2012年四川省数学高考文科试题)
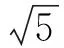
那么已知三边求角是否只能用余弦定理解决呢?当然不是,它同样也可以用正弦定理.不妨设△ABC中角A,B,C的对边分别是a,b,c,且a (2) (3) 根据式(1)还可以得到 asin(A+B)=csinA, 即 asinAcosB+acosAsinB=csinA. 将式(2),式(3)代入,整理得 即 又因为B是锐角,所以 继续代入,得 两边平方后整理,得 即 b2=c2+a2-2accosB. 从而可得角B的值,同理可得角A的值,最后得到角C. 评注类型(4)用余弦定理比用正弦定理简单很多,因此类型(4)通常采用余弦定理求解,用正弦定理也是可行的,只是路途曲折很多.在用正弦定理求解的过程中,最后推得的结果刚好就是余弦定理的结论. 正因为正弦、余弦定理是互通的、辩证统一的,所以解三角形的4类问题,其实都既可以用正弦定理去做,又可以用余弦定理去做.只是类型(1)和类型(2)用正弦定理做、类型(3)和类型(4)用余弦定理做,在计算过程上相对来说可略胜一筹,计算更便捷. [1] 刘清源.构建高效教学 探求数学本质——如何解好三角形[J].数学教学与研究,2011(36):78-79. [2] 覃埋基.一类解三角形问题的另一解法[J].数学通讯,2003(12):9.






