陶叶青 张 生 杨 娟

1)宿州学院煤矿勘探工程技术研究中心，宿州 234000

2)中国矿业大学环境与测绘学院，徐州 221008

顾及大地高误差的空间三维坐标系统转换*

陶叶青1，2)张 生1)杨 娟1)

1)宿州学院煤矿勘探工程技术研究中心，宿州 234000

2)中国矿业大学环境与测绘学院，徐州 221008

在参心坐标系向地心坐标系转换的过程中，由于控制点在参心坐标系中缺乏高精度的大地高，使得控制点在参心坐标系中的空间三维直角坐标存在误差，对转换结果有一定的影响，而应用最小二乘准则建立的空间转换模型没有顾及这一影响。对应用总体最小二乘建立空间转换模型实现坐标系统转换的方法进行了探讨，并用已知数据分别对总体最小二乘(TLS)与最小二乘(LS)算法实现坐标系统转换做出比较，结果显示，前者计算精度高、求解更合理。

大地高;总体最小二乘;最小二乘;坐标系统转换;高斯-马尔科夫模型

1 引言

目前，我国使用的坐标系有参心坐标系(北京54、西安80)与地心坐标系(CGCS2000)，坐标系统转换主要面对的是应用传统光学观测方法建立的二维参心坐标系向用GNSS方法建立的三维地心坐标系间的转换。为实现坐标系统之间的转换，通常借助平面转换模型［1］或三维空间转换模型［2］。转换模型参数通过控制点在两套坐标系统中的坐标值进行求解，当控制点数目大于必要观测数时，则应用最小二乘方法(LS)建立高斯-马尔科夫模型(G-M，Gauss-Markov)求解模型参数。

G-M模型求解转换参数的前提是控制点在原坐标系统中的坐标没有观测误差，将控制点在目标坐标系统中的坐标作为观测量，求解模型参数。应用空间三维转换模型时，由于控制点在参心坐标系中的大地高数值精度不高，导致控制点的空间三维直角坐标无法精确获得［3］，控制点在原坐标系统中不可避免地含有误差。根据最小二乘准则建立G-M模型无法顾及已知数据中含有的大地高误差，获得的模型参数精度不高。

总体最小二乘(TLS)能够顾及变量中含有误差(EIV，Error-In-Variables)的模型估计问题［4－7］，应用TLS准则实现坐标系的转换，能够同时对控制点在原坐标系统中大地高含有的误差以及目标坐标系中的观测误差进行最小化的约束。与假设控制点在原坐标系坐标没有误差的最小二乘相比，根据总体最小二乘建立的模型能够顾及控制点在目标坐标系与原坐标系中均含有的误差对转换结果的影响。

2 坐标转换数学模型与方法

2.1 坐标转换模型

空间三维坐标转换常用七参数转换模型［2］:

式中(X1，Y1，Z1)T与(X2，Y2，Z2)T分别为控制点在原坐标系与目标坐标系中的空间三维直角坐标，(X0，Y0，Z0)T为三个平移参数，(εX，εY，εZ)为三个旋转参数，δμ为尺度参数。应用GNSS技术进行坐标系统的转换，通常是在目标坐标系中的控制点上进行控制测量，获得控制点在目标坐标系中的空间三维直角坐标(X2，Y2，Z2)T。

当控制点数目多于两个时，将式(1)模型可表示为线性模型:

式(2)左边为控制点在目标坐标系统中的坐标向量l，右边第一项是以控制点在原坐标系中坐标做为参数的系数矩阵A，第二项为待求转换参数变量矩阵x。

2.2 最小二乘(LS)求解模型参数

当观测数目大于必要观测数时，最小二乘求解转换参数的前提是假设系数矩阵A没有观测误差，即控制点在原坐标系统中的坐标没有误差。观测向量l中含有偶然误差V，V服从正态分布。利用最小二乘法，建立G-M模型求解转换参数［8］:

式中σ20为变量的方差，P为观测向量的权阵。以最小二乘准则

求得转换参数，即变量矩阵x的解为:

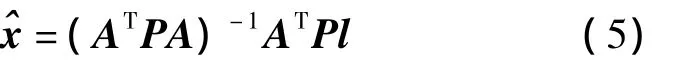
进一步可获得单位权方差与参数的协方差矩阵为:

式(6)中的r为多余观测量。应用G-M模型求解转换参数的前提是模型中的系数矩阵A没有误差。

2.3 总体最小二乘(TLS)求解模型参数

总体最小二乘能够顾及式(3)中系数矩阵A含有的观测误差，求解待估参数。设系数矩阵A含有的误差矩阵为b，建立模型:

式中vecb代表将系数矩阵的观测A误差矩阵b按列向量化，等权总体最小二乘的估计准则为:

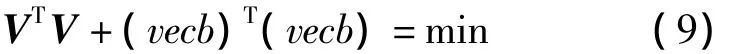
应用TLS求解转换参数时，通常采用奇异值分解(SVD，Singular Value Decomposition)的方法求解［9］。对增广矩阵［A，l］进行奇异值分解:

式中 U=［u1，u2，…，un］∈Rn×n是n×n阶正交矩阵，由［A，l］×［A，l］T的特征向量组成;V=［v1，v2，…，vn］∈R(m+1)×(m+1)是(m+1)× (m+1)阶正交矩阵，由［A，l］T×［A，l］的特征向量组成;∑ =diag［σ1，σ2，…，σm+1］为n× (m+1)阶的对角矩阵，对角线上的元素为奇异值，非对角线上的元素为0［10］。

为了应用TLS求得的转换参数x使目标函数式(9)最小，将式(8)改写成:

3 转换步骤与算例

3.1 转换步骤

应用GNSS技术改造、建设国家或地方参心坐标系控制网时，将参心坐标系的控制点坐标转换为地心坐标系的三维空间直角坐标，应用总体最小二乘(TLS)，结合转换模型式(1)进行坐标系的转换。转换步骤如下:

1)首先将参心坐标系的二维坐标(平面坐标或大地坐标)转换为空间三维直角坐标［11］;

2)应用GNSS技术进行控制测量，获得控制点在地心坐标系中的空间三维直角坐标或者控制点间的基线向量;

3)结合式(2)、(8)建立误差方程，根据式(10)～(12)求得转换参数的TLS解，实现坐标系转换;

4)根据式(14)与式(15)对转换结果进行精度评定。

3.2 算例

利用已知数据分别在最小二乘与总体最小二乘准则下建立G-M模型，已知点在WGS-84坐标系下的空间三维直角坐标与北京54坐标系下的大地坐标见表1［11］，LS与TLS求解模型转换参数的结果与精度见表2。

由表2可得，用最小二乘与总体最小二乘求解模型参数的数值相差不大，TLS计算得到的单位权中误差数值较小。这说明与无法顾及控制点在原坐标系统中的坐标误差的最小二乘算法建立的G-M模型相比，根据TLS建立的模型求解转换参数更加科学、合理。

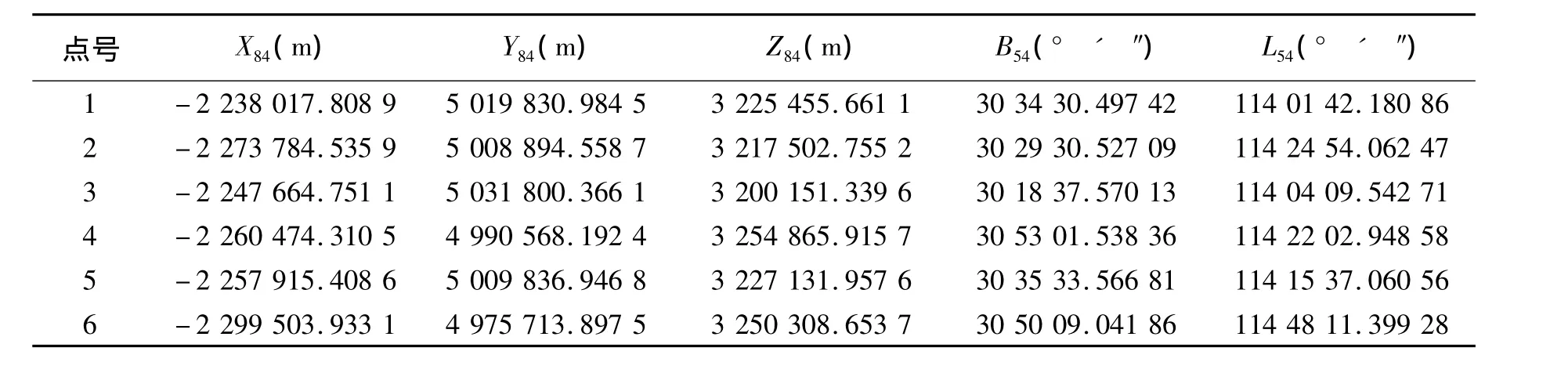
表1 控制点在不同坐标系下的坐标Tab.1 Coordinates of control points in different coordinate systems

表2 LS与TLS求解转换参数与精度评定Tab.2 Solving parameters and the accuracy estimation of LS and TLS

4 结论

1)结合LS、TLS，给出适合我国参心坐标系与地心坐标系间转换的空间三维直角坐标转换方法。

2)应用TLS建立的模型由于顾及了控制点在参心坐标系中的大地高误差，求解转换模型的参数以及中误差比应用LS方法计算结果精度高，求解更合理。

3)在求解模型参数时，将控制点在原坐标系统与目标坐标系统中的坐标当作等精度处理，没有顾及控制点间的坐标精度也是不等的现实，这需要在以后的研究工作中解决。

1 姚宜斌.平面坐标系统相互转换的一种简便算法［J］.测绘信息与工程，2001，(1):1 －3.(Yao Yibin.A simple and convenient arithmetic for the transformation of plane coordinate system［J］.Journal of Geomatics，2001，(1):1 －3)

2 刘大杰、施一民、过静珺.全球定位系统的原理与数据处理［M］.上海:同济大学出版社，1996.(Liu Dajie，Shi Yiming and Guo Jingjun.Principle and data processing of GPS［M］.Shanghai:Tongji University Press，1996)

3 施一民.现代大地控制测量［M］.北京:测绘出版社，2003.(Shi Yiming.Geodesy and control survey［M］.Beijing:Surveying and Mapping Press，2003)

4 Felus Y A and Schaffrin B.Performinng similarity transformations using the error-in-variables model［R］.ASPRS 2005 Annual Conference Baltimore，Maryland，2005.

5 De Groen P.An introduction to total least squares［M］.Niew Archiefvoor Wiskunde，Vierde serie deel，14，1996.

6 Van Huffel S and V andeualle J.The total least squares problem［J］.Computational Aspects and Analysis，Frontiers in Applied，Mathematics，SIAM，Philadelphia，1991，9:34 －35.

7 Schaffrin B.A note on constrained total least-squares estimation［J］.Linear A lgebra and Its Applications，2006，65(3):141－168.

8 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2003.(Surveying Adjustment Research Group of Wuhan University.Basis of error theory and measurement adjustment［M］.Wuhan:Wuhan U-niversity Press，2003)

9 Golub H G and Van Loan F C.An analysis ofthe total least squares problem［J］.SIAM Journal on Numerical Analysis，1980，17(6):883 －893.

10 程云鹏.矩阵论［M］.西安:西北工业大学出版社，2000.(Cheng Yunpeng.Matrix theory［M］.Xi’an:Northwestern Polytechnical University Press，2000)

11 谢鸣宇、姚宜斌.三维空间与二维空间七参数转换参数求解新方法［J］.大地测量与地球动力学，2008，(2):104－109.(Xie Mingyu and Yao Yibin.A new method for solution of seven-parameter transformation between 3D and 2D spaces［J］.Journal of Geodesy and Geodynamics，2008，(2):104－109)

3D SPACE COORDINATE SYSTEM TRANSFORMATION CONSIDERING GEODETIC ELEVATION ERROR

Tao Yeqing1，2)，Zhang Sheng1)and Yang Juan1)
1)Engineering Research Center of Coal Mining Exploration，Suzhou University，Suzhou230000
2)School of Environment Science and Spatial Informatics，China University of Mining
and Technology，Xuzhou221008

In the transformation from national reference-ellipsoid-centric coordinate to national geocentric coordinate，the lack of precise geodetic elevation of control points in reference-ellipsoid-centric coordinate makes the rectangular space coordinates of control points contain error.And this factor has an impact on final conversion accuracy.Up to late the 3D space coordinate model based on least squares has not taken into account the influence.In this paper，we discuss the method of 3D space coordinate transformation based on total least squares，besides，compare the methods of coordinate transformation based on total least squares and least squares used known data.The result shows that the accuracy of the former is better than the later.

geodetic elevation;total least squares(TLS);least squares(LS);coordinate system transformation;Gauss-Markov model

P221

A

1671-5942(2013)04-0096-04

2012-11-18

国家自然科学基金(41074010);安徽省煤矿勘探工程技术研究中心开题课题(2012YKF11;2013YKF03)

陶叶青，男，1984年生，助教，博士研究生，主要研究方向:GNSS导航与测量数据处理.E－mail:yenneytao@163.com