苏锦钿 余珊珊

(1．华南理工大学计算机科学与工程学院，广东广州510006;2．中山大学信息科学与技术学院，广东广州510275)

范畴数据类型(CDT)研究是指以范畴论为数学理论基础研究数据类型的描述、计算语义、构造或行为特征、数学性质及其在计算机科学中的应用等．CDT主要包括归纳数据类型［1］(如自然数、有限分支树、链表和队列等)和共归纳数据类型［2-3］(如无限的流、链表、堆栈和树等)．归纳数据类型研究是指利用代数研究递归类型中有限数据类型的构造语义及其递归性质．共归纳数据类型研究是指利用共代数研究共递归类型中无限数据类型的行为语义及其共递归性质．

作为类型理论研究的一个核心概念，代数子类型描述了两个归纳数据类型在构造操作下的一种结构保持关系，而共代数子类型则描述了两个共归纳数据类型在观察操作下的一种行为保持关系．Poll［4］对归纳数据类型上的子类型进行了研究，并将代数子类型引入到范畴数据类型中，给出了共归纳数据类型间的共代数子类型定义及相应的终结共代数语义解释．

对许多CDT来说，除了包含构造操作外，还包含观察操作，即同时具有归纳和共归纳数据类型的典型特征．Erwig［5］指出，每个抽象数据类型都可描述成一个双代数，并探讨了以共代数函子为参数的递归操作．Nogueira等［6］利用双代数对抽象数据类型进行描述，并探讨了它们的双代数结构在多态编程中的应用．笔者在前期研究中发现:双代数可以给出数据类型上构造操作和观察操作的统一描述，并结合分配律探讨了归纳与共归纳数据类型、fold与unfold之间的关系［7-8］．上述研究均没有分析包含构造和观察操作的数据类型间的子类型关系及其性质，也没有给出双代数结构中的子类型定义及语义解释．

为此，文中分析了归纳数据类型上的代数子类型和共归纳数据类型上的共代数子类型的范畴论定义及其语义，并利用双代数给出了CDT上构造操作和观察操作的一种抽象描述;然后，将代数子类型和共代数子类型扩展到基于双代数的CDT上，给出了它们在双代数中的定义及其语义解释．

1 范畴数据类型及子类型

为便于描述，文中用F、G和H表示代数函子，B、D和E表示共代数函子，α、φ和δ分别表示函子F、G和H的基调，β、φ、σ分别表示函子B、D和E的基调，αX和αY分别表示同一函子F在不同载体集X和Y上的基调．

1．1 归纳数据类型及代数子类型

归纳数据类型可以表示为代数，其中代数函子给出了数据类型上各种构造操作的抽象描述．

定义1 给定范畴 和函子F: ，F-代数定义为二元组(X，αX:FX X)，其中X是 中的对象，称为该F-代数的载体;αX是 中的射，称为该F-代数的基调．任意两个 F-代数(X，αX)和(Y，αY)间的同态射 f:(X，αX)(Y，αY)是 中的射 f:XY，且满足f◦αX= αY◦Ff．

在范畴论视角下，每个归纳数据类型恰好是某个代数函子的初始代数，且为递归类型等式的最小不动点．

定义2 给定函子 F: ，称(μF，inF:FμF μF)为初始F-代数，当且仅当对于任意一个F-代数(X，αX)，存在唯一射 foldF(αX):μF X，使得图 1 中的图表满足交换条件．其中，foldF(αX)是由基调αX所确定的迭代射，在函数式程序语言中也称为fold射［9］或 catamorphism［1］．

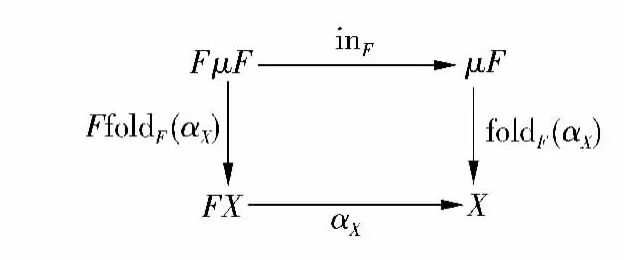
图1 初始代数及唯一射Fig．1 Initial algebras and the unique morphism

例1 参数化数组AList上的初始化操作(nil:1AList)和插入操作(cons:A×AListAList)可抽象地描述为代数函子ListF(X)=1+A×X，且AList为初始 ListF-代数，记为 ListAlg=(AList，inListF=［nil，cons］)，其中 A为某个已知的数据类型，如整型、字符串或布尔类型．

对归纳数据类型来说，代数子类型是指子数据类型上的构造操作在父数据类型中得到保持，可理解为两个归纳数据类型间存在一个满足合适条件的射，将每个子数据类型的元素映射为父数据类型的元素．例如，若类型A是类型A'的代数子类型，记为A≤AlgA'，则意味着A的元素同时也是A'的元素．一方面，子数据类型A上的所有构造操作都包含在父数据类型A'中;另一方面，由A中的构造操作所得到的元素，均可以由A'中的对应构造操作得到．在集合范畴中，可理解为A的元素构成了A'的元素的子集，即看成是类型间的一个自然包含关系．

定理1［4］给定两个函子 F，G: ，(μF，inF)和(μG，inG)分别为相应函子的初始F-代数和初始G-代数．若存在自然转换 η:F⇒G，则有唯一射foldF(inG◦ημG):μF μG，使得图 2 中的图表满足交换条件．

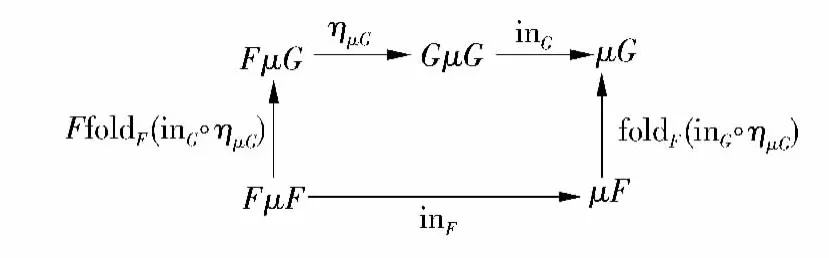
图2 初始代数间的射Fig．2 Morphism between initial algebras

定理1给出了归纳数据类型上代数子类型的初始代数语义解释，其中foldF(inG◦ημG)就是从子数据类型到父数据类型的唯一射coerce:μF μG．在子类型研究中，射coerce通常称为隐式抑制射［10-12］．

例2 参数化数组AZList上的初始化操作(znil:1AZList)、插入操作(zcons:A×AZListAZList)和合并操作(zip:AZList×AZListAZList)可抽象地描述为代数函子 ListG(X)=1+A×X+X×X，且AZList为初始 ListG-代数，记为 ZListAlg=(AZList，inListG=［znil，zcons，zip］)，其中 znil和 zcons与 AList上的nil和cons相同，zip表示依次将两个链表中的头元素取出并构成一个新的链表．

图3 ListAlg到ZListAlg的映射Fig．3 Mapping from ListAlg to ZListAlg

对于初始ListF-代数ListAlg和初始ListG-代数ZListAlg，存在自然转换［in1，in2］:ListF ListG．再由定理1可得到唯一射coerce:AListAZList，使得图3中的图表均满足交换条件，即ListAlg≤AlgZListAlg成立．其中，ini:XiX1+X2+… +Xn是第 i(1≤i≤n)个分量到其共积的注入射XnXi为ini的逆，用于取出共积中的第i个分量，且满足 in-1i◦ini=IdXi．由于射 coerce:AListAZList满足coerce◦nil=znil和 coerce◦cons=zcons◦IdA×coerce，因此有ListAlg≤AlgZListAlg．这意味着 ListAlg中所有由nil和cons所构造出来的元素，均可由ZListAlg中的对应znil和zcons构造而成．

1．2 共归纳数据类型及共代数子类型

对偶地，共归纳数据类型可表示为共代数，其中共代数函子给出了数据类型上各种观察操作的抽象描述．

定义3 给定范畴 和函子B: ，B-共代数定义为二元组(X，βX:X BX)，其中 X∈ 称为该B-共代数的载体或状态空间，射βX称为该B-共代数的基调或变迁射．任意两个B-共代数(X，βX)和(Y，βY)间的同态射f:(X，βX)(Y，βY)是 中的射f:X Y，且满足 Bf◦βX=βY◦f．

在范畴论视角下，每个共归纳数据类型恰好是某个共代数函子的终结共代数，且为共递归类型等式的最大不动点．

定义4 给定函子 B: ，称(νB，outB:νB BνB)为终结B-共代数，当且仅当对任意一个B-共代数(X，βX)，存在唯一射 unfoldB(βX):X νB，使得图4中的图表满足交换条件．其中，unfoldB(βX)是由基调βX所确定的共迭代射，也称为unfold射［9］或anamorphism［1］．

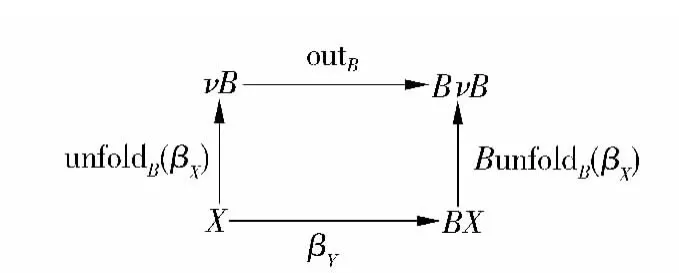
图4 终结共代数及其唯一射Fig．4 Final coalgebras and its unique morphism

例3 参数化数组CList上的观察操作包括isnil:CList1+1(用于判断数组是否为空)、head:CListA(用于给出数组的当前元素)、tail:CListCList(用于给出数组的剩余部分)、reverse:CListCList(用于对数组CList进行逆转)．这些操作可抽象地描述为共代数函子ListD(X)=1+A×X+X，且CList为终结 ListD-共代数，ListCoalg=(CList，outListD=〈isnil，〈head，tail〉，reverse〉)，其中 outListD=(1+(〈head，tail〉+reverse))◦isnil?．

对共归纳数据类型来说，共代数子类型是指父数据类型上的行为在子数据类型中得到保持，即可理解为两个共归纳数据类型间存在一个满足合适条件的抑制射．例如，若A是B的共代数子类型，记为A≤CoalgB，则父数据类型B上的可观察行为在子数据类型A中得到保持．一方面，B上的所有观察操作均包含在A中;另一方面，B中元素的可观察行为均可以由A中对应元素上的观察操作得到．即共代数子类型体现了共归纳数据类型在观察操作下的一种行为保持关系．

定理2［4］给定两个函子 B和 D: ，(νB，outB)和(νD，outD)分别为相应函子的终结B-共代数和D-共代数．若存在自然转换ρ:D⇒B，则有唯一射unfoldB(ρνD◦outD):νD νB，使得图 5 中的图表满足交换条件．

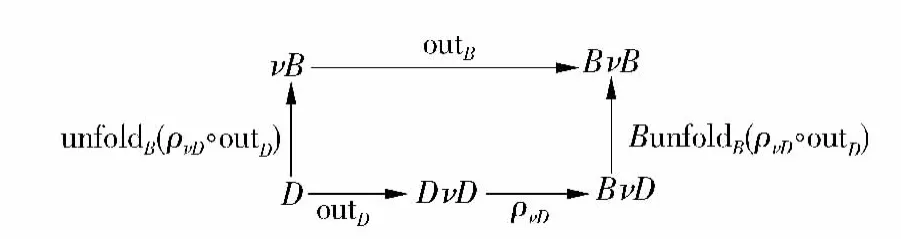
图5 终结共代数间的射Fig．5 Morphism between final coalgebras

定理2给出了共归纳数据类型上共代数子类型的终结共代数语义解释，其中 unfoldB(ρνD◦outD)就是从子数据类型到父数据类型的抑制射．

给定两个共归纳数据类型 C1=(νB，outB)和C2=(νD，outD)，若只存在自然转换 ρ:D⇒B，则称C1是C2的基调子类型，强调方法的重用;若存在自然转换ρ:D⇒B及抑制射coerce:νD νB，使得图5中的图表满足交换条件，则称C1是C2的行为子类型［13］，强调行为的保持及客户端代码的重用．在面向对象设计原则中，行为子类型构成了Liskov替换原则的基础．

例4 参数化数组CZList上的观察操作zisnil:CZList1+1、zhead:CZListA 和 ztail:CZListCList可表示为共代数函子 ListB(X)=1+A×X，且CZList为对应的ListB-终结共代数，记为ZListCoalg=(CZList，outListB= 〈zisnil，〈zhead，ztail〉〉)，其 中outListB=(1+〈zhead，ztail〉)◦zisnil?．

显然，对于终结ListD-共代数ListCoalg和终结ListB-共代数 ZListCoalg，存在自然转换〈1，2〉:ListD ListB．再由定理2可得到唯一射 coerce:CListCZList，使图6中的所有图表满足交换条件，即满足 zisnil◦coerce=isnil，zhead ◦coerce=head 和ztail◦coerce=coerce ◦tail，因此ListCoalg≤CoalgZListCoalg成立．即 ZListCoalg中所有由 zisnil和〈zhead，ztail〉操作所观察得到的行为，均可以由ListCoalg中对应元素上的观察操作 isnil和〈head，tail〉得到．其中，i:X1×X2×…×XnXi是积到第 i个分量的投影射:XiX1×X2×… ×Xn为 i的逆，用于将第i个分量映射到积中的对应位置，且满足i=

图6 ListCoalg到ZListCoalg间的映射关系Fig．6 Mapping relationship between ListCoalg and ZListCoalg

1．3 范畴数据类型的双代数结构

各种归纳或共归纳数据类型通常既包含了可由代数描述的构造操作，也包含了可由共代数描述的观察操作，因此文中利用双代数给出一种统一的和抽象的描述．

定义5 给定范畴 上的两个函子F和B: ，〈F，B〉-双代数定义为三元组(X，αX:FX X，βX:X

BX)，其中 αX和 βX分别为同一载体集 X∈ 上的F-代数和 B-共代数．任意两个〈F，B〉-双代数(X，αX，βX)和(Y，αY，βY)间的同态射是范畴 中的射f:X Y，且满足 f◦αX=αY◦Ff和 Bf◦βX=βY◦f．

在完全偏序范畴中，初始代数和终结共代数上的载体恰好相同，且均为有限的，因此可用一个载体集同时表示有限及无限元素．即若范畴 为完全偏序范畴，则函子F: 的初始F-代数(μF，inF)和终结 F-共代数(νF，outF)满足 μF=νF，而 inF和 outF均为同构射且互逆．例如，参数化数组 AList和CZList上的函子ListF和ListB相同，因此其载体集AList和CZList相同，且 inListF与 outListB互逆，并可构成双代数(AList，inListF，outListB)或(CZList，inListF，outListB)．

由 Lambek 定理［14］可知，初始代数(μF，inF)上的基调inF是同构射，其逆in-1F:μF FμF给出了初始代数载体集上的观察操作，并构成一个共代数(μF，in-1F)，即(μF，inF，in-1F)为一个〈F，F〉-双代数．对偶地，由文献［15］中的定理9．1可知，终结共代数(νB，outB)上的基调outB是同构射，其逆out-1B:BνB νB给出了终结共代数载体集上的构造操作，并构成一个代数(νB，out-1B)，即(νB，out-1B，outB)为一个〈B，B〉-双代数．任意的归纳或共归纳数据类型均可通过上述方式扩展为双代数．

例5 利用共代数函子ListD和ListB可分别将AList和AZList扩展为相应的〈ListF，ListD〉、〈ListG，ListD〉和〈ListG，ListB〉-双代数:

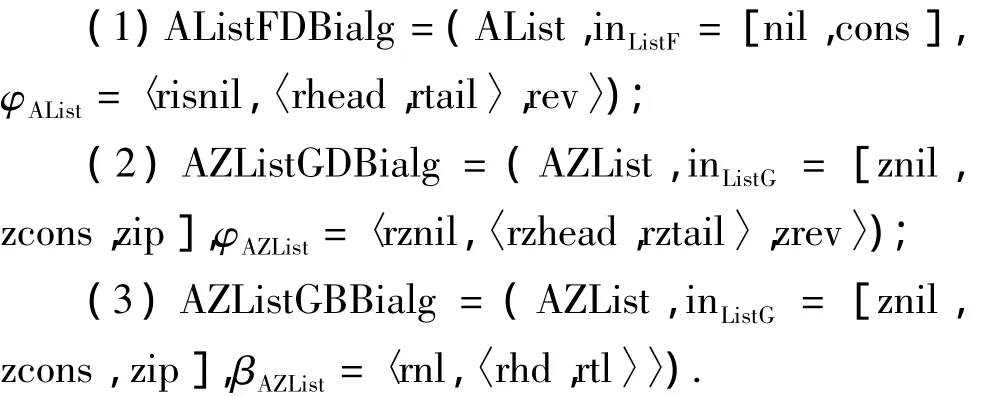
类似地，利用代数函子ListF或ListG可将CList和 CZList扩展为相应的〈ListF，ListD〉和〈ListF，ListB〉-双代数:

定义6 范畴数据类型T1=(X，αX，βX)和T2=(Y，αY，βY)之间的共积和积合并算子分别定义为

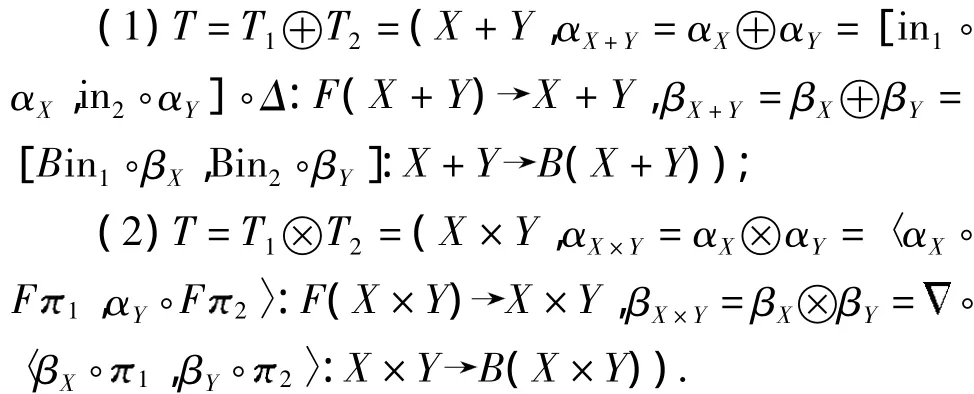
IdF(X+Y)］:F(X+Y)FX+FY，用于分离两个代数构造操作中的参数．例如，对于代数函子FX=1+A×X+X ×X，Δ 定义为:Δ(*)=*+* ，Δ(a，x+y)=(a，x)+(a，y)，Δ(x1+y1，x2+y2)=(x1，x2)+(y1，y2)．操作符 :BX×BYB(X×Y)用于合并两个观察结果．例如，对于函子BX=1+A×X+X，定义为:(* ，*)=* ，(〈a，x〉，〈a，y〉)=〈a，(x，y)〉，(x，y)=(x，y)．

2 双代数中的子类型

2．1 双代数中的代数子类型

定义7 给定两个不同的CDT，即T1=(X，φX:GXX，βX:X BX)和 T2=(Y，αY:FY Y，βY:YBY)，若存在自然转换η:F⇒G和唯一射coerce:X Y，使得图7中的图表满足交换条件，即coerce:X Y 是从(X，αX，βX)到(Y，φY◦ηY，βY)的双代数同态射，则称T1是T2在双代数中的代数子类型，记为T1≤Bia，AlgT2．

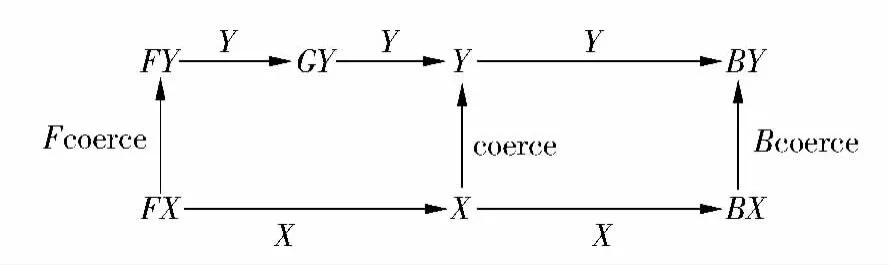
图7 双代数中的代数子类型Fig．7 Algebraic subtype in bialgebras

双代数中的代数子类型是指其中的代数结构存在子类型关系，且从子类型到父类型的抑制射为共代数同态射．换句话说，子类型中的构造在父类型中得到保持，且这些构造操作在共代数观察操作下不可区分．

定理3 给定初始〈F，B〉-双代数(μF，inF，βμF:μF BμF)和初始〈G，B〉-双代数(μG，inG，βμG:μG BμG)，若存在自然转换 η:F⇒G，则有唯一射f=foldF，B(inG◦ημG，βμG):μF μG，使得图 8 中的图表满足交换条件．

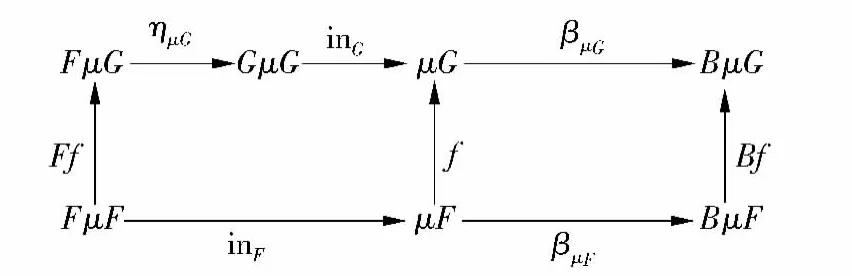
图8 初始双代数间的射Fig．8 Morphism between initial bialgebras

证明 由初始双代数的初始性可得到唯一射

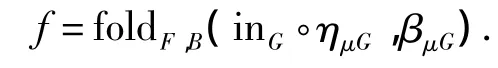
证毕．

定理3给出了归纳数据类型的双代数结构中代数子类型的初始双代数语义解释，其中foldF，B(inG◦ημG，βμG)就是从子类型到父类型的抑制射．

例如，对于AListFDBialg和AZListGDBialg，存在自然转换［in1，in2］:ListF ListG和唯一射 coerce:AListAZList，使得 coerce是从〈ListF，ListD〉-双代数(List，inListF，φAList)到(AZList，inListG◦［in1，in2］，φAZList)的双代数同态射，且满足:①isnil◦nil=rznil◦znil;②head ◦cons(a，x)=rzhead ◦zcons(a，coerce(x));③coerce ◦tail◦cons(a，x)=rztail◦zcons(a，coerce(x));④coerce ◦rev ◦cons(a，x)=zrev ◦zcons(a，coerce(x))．因此，AListFDBialg≤Bia，AlgAZListGDBialg 成立．

定理4 双代数中的代数子类型≤Bia，Alg关系满足自反性和传递性:

(1)T≤Bia，AlgT(自反性);

(2)T1≤Bia，AlgT2∧T2≤Bia，AlgT3⇒T1≤Bia，AlgT3(传递性)．

证明 (1)对任意的范畴数据类型T=(X，αX，βX)，均存在标识射IdX:X X和标识自然转换IdF:F⇒F，且 IdX是从(X，αX，βX)到(X，αX◦IdFX，βX)的双代数同态射．

(2)对任意的范畴数据类型 T1=(X，αX，βX)、T2=(Y，φY，βY)和 T3=(Z，δZ，βZ)，由前提可知，存在射f:XY、g:YZ及自然转换η:F⇒G和 :G⇒H．由射之间的组合性及自然转换保持射组合的性质可知:g ◦f:XZ 和 ◦η:F H，且 g ◦f是从(X，αX，βX)到(Z，δZ◦Z◦ηZ，βZ)的双代数同态射．再由定义 7可知 T1≤Bia，AlgT3成立．证毕．

定理5 对于范畴数据类型T1=(X，αX，βX)、T2=(Y，αY，βY)和 T3=(Z，φZ，βZ)，若满足T1≤Bia，AlgT3和 T2≤Bia，AlgT3，则有 T1⊕T2≤Bia，AlgT3．

证明 由前提可知，存在射f:X Z、g:Y Z和自然转换η:F⇒G．利用共积可得到唯一射［f，g］:X+Y Z．再由自然转换保持射的性质可知，［f，g］是从(X+Y，αX⊕Y，βX⊕Y)到(Z，φZ◦ηZ，βY)的双代数同态射．因此，由定义 7 可知 T1⊕T2≤Bia，AlgT3成立．证毕．

2．2 共代数子类型

定义8 给定两个 CDT，即 T1=(X，αX，φX)和T2=(Y，αY，βY)，若存在自然转换 ρ:D⇒B 和唯一射coerce:X Y，使得图9中的图表满足交换条件，即coerce:X Y 是从(X，αX，ρX◦φX)到(Y，αY，βY)的双代数同态射，则称T1是T2在双代数中的共代数子类型，记为 T1≤Bia，CoalgT2．

双代数中的共代数子类型是指其中的共代数结构存在子类型关系，并且从子类型到父类型的抑制射为代数同态射．换句话说，双代数中的共代数子类型是指在保持数据类型上的构造操作不变的前提下，父类型中的行为在子类型中得到保持．

定理 6 给定终结〈F，B〉-双代数(νB，ανB，outB)和终结〈F，D〉-双代数(νD，ανD，outD)，若存在自然转换 ρ:D⇒B，则有射 f=unfoldF，B(ανD，ρνD◦outνD):νD νB，使得图10中的图表满足交换条件．

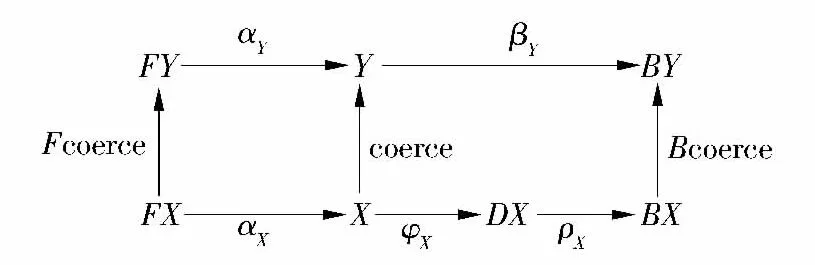
图9 双代数中的共代数子类型Fig．9 Coalgebraic subtype in bialgebras

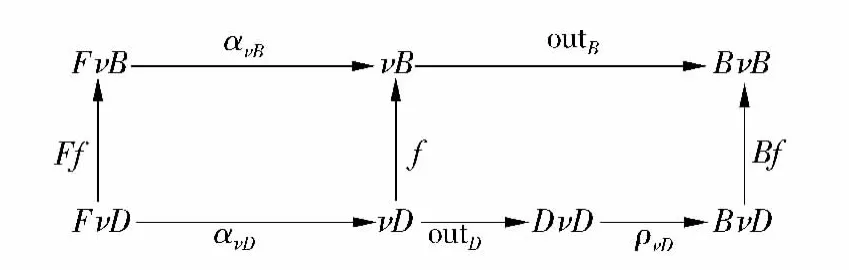
图10 终结双代数间的射Fig．10 Morphism between final bialgebras

证明 由终结双代数的终结性可得到

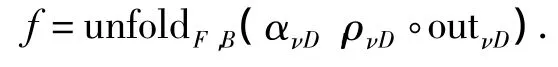
证毕．

定理6给出了共归纳数据类型的双代数结构中共代数子类型的终结双代数语义解释，unfoldF，B(ανD，ρνD◦outνD)就是从子数据类型到父数据类型的抑制射．

例如，对于CListFDBialg和CZListFBBialg，存在自然转换〈1，2〉:ListD ListB和唯一射 coerce:CZListCList，使得 coerce 是从〈ListF，ListB〉-双代数(CList，αCList，〈1，2〉◦outListD)到(CZList，αCZList，outListB)的双代数同态射，且满足:①isnil◦rnil=zisnil◦rznil;②head ◦rcons(a，x)=zhead ◦rzcons(a，coerce(x));③coerce ◦tail◦rcons(a，x)=ztail◦rzcons(a，coerce(x))．因此，CListFDBialg≤Bia，CoalgCZListBialg 成立．

定理7 双代数中的共代数子类型满足自反性和传递性:

(1)T≤Bia，CoalgT(自反性);

(2)T1≤Bia，CoalgT2∧T2≤Bia，CoalgT3⇒T1≤Bia，CoalgT3(传递性)．

证明 (1)由标识射为双代数同态射及标识自然转换的性质可得T≤Bia，CoalgT．

(2)对于任意的范畴数据类型T1=(X，αX，βX)、T2=(Y，αY，φY)和 T3=(Z，αZ，σZ)，由前提可知，存在射f:XY和g:YZ，以及自然转换 ρ:E⇒D和θ:D⇒B．由射之间的组合性及自然转换保持射组合的性质可知，g◦f:X Z 和 θ◦ρ:E⇒B，且 g ◦f是从(X，αX，θX◦ρX◦βX)到(Z，αZ，βZ)的双代数同态射．再由定义8可知 T1≤Bia，CoalgT3成立．证毕．

定理8 对于范畴数据类型T1=(X，αX，φX:X DX)、T2=(Y，αY，βY:Y BY)和 T3=(Z，αZ，βZ:Z

BZ)，若 满 足 T1≤Bia，CoalgT2和 T1≤Bia，CoalgT3，则 有T1≤Bia，CoalgT2⊗T3．

证明 由前提可知，存在射f:X Y、g:X Z和自然转换 ρ:D⇒B．利用积可得到唯一射〈f，g〉:X Y×Z．再由射之间的组合性及自然转换保持射组合的性质可知，〈f，g〉是从(X，αX，ρX◦σX)到(Y ×Z，αY⊗Z，βY⊗Z)的双代数同态射．因此，T1≤Bia，CoalgT2⊗T3成立．证毕．

3 结语

将子类型引入到基于双代数的CDT中，一方面可以为研究归纳数据类型间的代数子类型和共归纳数据类型间的共代数子类型提供一个统一的数学理论框架，更好地探讨包含构造操作和观察操作的数据类型之间的关系及性质，从而促进CDT在函数式程序语言和泛化编程等领域中的应用;另一方面可以从范畴论的角度给出子类型的数学定义和语义解释．今后将研究如何将子类型扩展到其他各种CDT(如嵌套或依赖数据类型)上，并探讨子类型与继承之间的关系及性质．

［1］Meijer E，Fokkinga M，Paterson R．Functional programming with bananas，lenses，envelopes and barbed wire［C］∥Hughes J．Functional Programming Languages and Computer Architecture．New York:Springer-Verlag，1991:124-144．

［2］苏锦钿，余珊珊．程序语言中的共归纳数据类型及其应用 ［J］．计算机科学，2011，38(11):114-118．Su Jin-dian，Yu Shan-shan．Coinductive data types and their applications in programming languages［J］．Computer Science，2011，38(11):114-118．

［3］苏锦钿，余珊珊．共归纳数据类型上的共递归操作及其计算定律［J］．华南理工大学学报:自然科学版，2011，39(10):90-95．Su Jin-dian，Yu Shan-shan．Corecursion operations and its calculation laws on coinductive data types［J］．Journal of South China University of Technology:Natural Science Edition，2011，39(10):90-95．

［4］Poll E．Subtyping and inheritance for inductive types［C］∥Proceedings of TYPES＇97 Workshop on Subtyping，Inheritance and Modular Development of Proofs．Durham:University of Durham，1997:1-10．

［5］Erwig M．Metamorphic programming:structured recursion for abstract data types［R］．Hagen:Computer Science Department，Fern University，1998:20-30．

［6］Nogueira P，Moreno-Navarro J J．Bialgebra views:a way for polytypic programming to cohabit with data abstraction［C］∥Proceedings of the ACM SIGPLAN Workshop on Generic Programming．New York:ACM，2008:61-73．

［7］苏锦钿，余珊珊．抽象数据类型的双代数结构［J］．华南理工大学学报:自然科学版，2011，39(12):1-7．Su Jin-dian，Yu Shan-shan．Bialgebraic structure of abstract data types［J］．Journal of South China University of Technology:Natural Science Edition，2011，39(12):1-7．

［8］苏锦钿，余珊珊．抽象数据类型的双代数结构及其计算定律［J］．计算机研究与发展，2012，49(8):1787-1803．Su Jin-dian，Yu Shan-shan．Bialgebraic structures for abstract data types and their computations［J］．Journal of Computer Research and Development，2012，49(8):1787-1803．

［9］Gibbons J，Hutton G，Altenkirch T．When is a function a fold or an unfold?［J］．Electronic Notes in Theoretical Computer Science，2001，44(1):146-160．

［10］Luo Z．Coercive subtyping ［J］．Journal of Logic and Computation，1999，9(1):105-130．

［11］Luo Z．Coercive subtyping in type theory［C］∥Proceedings of the 1996 Annual Conference of the European Association for Computer Science Logic．London:Springer-Verlag，1996:276-296．

［12］Xue T．Theory and implementation of coercive subtyping［D］．Royal Holloway:Department of Computer Science，University of London，2013．

［13］Poll E．A coalgebraic semantics of subtyping［J］．Theoretical Informatics and Applications，2001，35(11):61-81．

［14］Lambek J．A fixpoint theorem for complete categories［J］．Mathematische Zeitschrift，1968，103:151-161．

［15］Rutten J J M M．Universal coalgebra:a theory of systems［J］．Theoretical Computer Science，2000，249(1):56-58．