邹 磊，郑林华，林嘉宇，丁 宏

(国防科学技术大学电子科学与工程学院，长沙 410073)

1 引言

跳频序列是跳频通信系统的基础和核心，它保证了跳频通信系统的高抗干扰和低截获概率性能，故而对跳频序列的研究至关重要。传统的跳频序列分析方法，主要分析跳频序列的Hamming相关、平衡特性、宽间隔特性和线性复杂度等跳频特性［1－2］。而对于来自不同生成方法的跳频序列却不应局限于这些分析方法。混沌跳频序列［3］来自于确定性系统，却表现出很强的随机性，这正是混沌信号的特征［4］。混沌跳频序列产生于混沌系统，若其具有混沌性，则可以利用相空间重构理论［5］对其重构，并可得到与原系统等价的系统，进一步，可通过分析该等价系统得到原系统的一些特性信息。

2 混沌性判别

混沌信号具有对初始值的敏感性、有界性、非周期性以及确定性等要求，这是构成混沌信号生成系统的必要条件。而在实际应用中，通常将这些判别方法适当的放松，即可足够满足实际工程要求［6］。

初始值的敏感性，可由Lyapunov 指数描述，表示不同初值的混沌信号在一段时间的演化后其轨迹的收敛与发散程度，一般为正值，说明系统产生混沌信号的可能性较大;信号的有界性，实际系统通常可以满足，不需要再进行判断;信号的非周期性，混沌信号的吸引子一般具有自相似性，可用分形维来描述，而且一般情况下分形维是非整数;信号的确定性，确定性信号的维数通常是有限的，其分形维也应当是有限的，另外，确定性的系统是可以实现局部预测的，混沌信号由于其初值敏感性和现实环境中的噪声等因素影响，不可能对其进行长期预测，但可以进行局部预测，这样，有限的分形维和局部可预测性可以区分确定信号与随机信号，而在实际工程中产生的信号一般均可满足局部可预测性。

由此得到，从工程实用上来说，分析信号具有正的Lyapunov 指数和有限且为非整数的分形维即可认为该信号具有混沌性。

2.1 Lyapunov 指数的小数据量法

混沌系统对初值具有高度的敏感性，可用Lyapunov 指数表征，它描述两个相近初值所产生的轨道，随着时间演化按指数方式分离的量，一般分析最大Lyapunov 指数为正值即可。此处分析选择小数据量法，小数据量法［7］计算方便、操作简单，对相空间的嵌入维数、时间延迟、观测噪声等表现了较好的鲁棒性，对小数据量也比较可靠，具体描述如下。

设混沌序列为{x1，x2，...，xN}，嵌入维数m，延迟时间τ，则经重构后得到相空间如下:

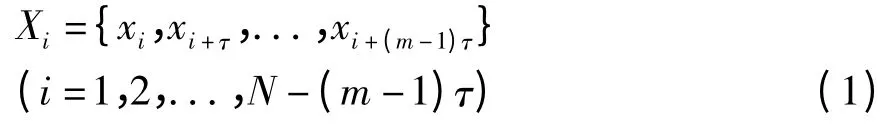
重构相空间后，寻找给定轨道上每个点的最近邻近点，即:

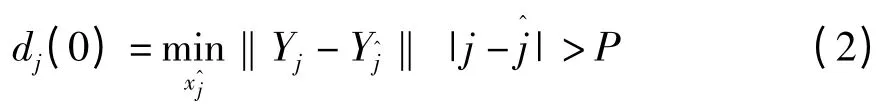
其中，P为序列的平均周期，它可以利用能量谱的平均频率的倒数估算出来。最大Lyapunov 指数则可通过基本轨道上每个点的最近邻点的平均发散速率估算得到。估算最大Lyapunov 指数式为:

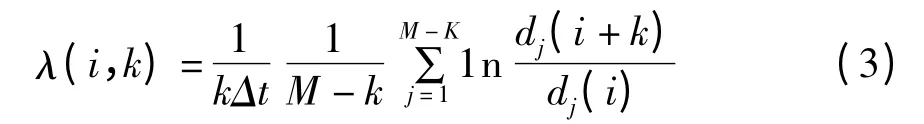
其中Δt为信号采样周期，k为常数，dj(i)是基本轨道上第j 对最近邻近点对经过i个离散时间步长后的距离:

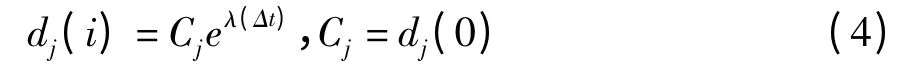
将式(4)两边取对数得到:

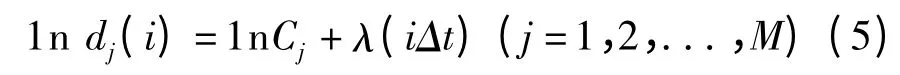
式(5)中函数的斜率即为所求的最大Lyapunov指数，可以通过最小二乘法拟合这条曲线得到，即:

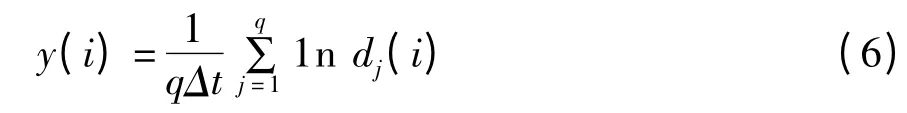
其中，q为非零dj(i)的数目。考虑f=y(i)的一阶导数:

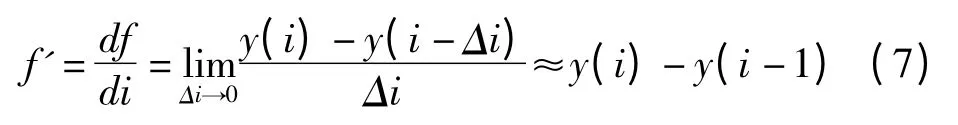
理想情况下，如果i～y(i)满足线性关系，f'应当为一常数。在i～y(i)达到饱和之前，选i～y(i)－y(i－1)曲线图中变化较小的一段区域为线性区域，此段区域的斜率即是最大Lyapunov 指数。

2.2 分形维的G－P 算法

由于混沌系统的吸引子具有自相似性，它在空间的演化过程中不断的靠拢分离，形成和前一轨迹相似的结构，而且每一个轨迹都和整体有相似性。混沌信号的相空间图一般都是分形体，描述混沌系统吸引子的自相似一般使用分形维，分形维有多种定义，有Hausdoff 维、关联维、自相似维、盒子维、Lyapunov 维、信息维和点形维。其中，以关联维(Correlation Dimension)最为常用，而计算关联维数的常用方法为G－P 算法［8］，下面具体描述。

(1)给定混沌序列{x1，x2，...，xN}，先选取一个较小的值m0，对应得到一个重构的相空间;

(2)计算关联函数:

其中，|Y(ti)－Y(tj)|表示相空间中点Y(ti)和Y(tj)之间的距离;θ(z)是Heaviside 函数，当z≥0时，θ(z)=1，当z ＜0时，θ(z)=0;C(r)是一个累积分布函数，表示相空间中吸引子上两点之间距离小于r的概率。

(3)当r 取某一适当范围时，吸引子的维数d 与累积分布函数C(r)应满足对数线性关系，即d(m)=1nC(r)/1nr。然后据此可以拟合出对应于m0的关联维数估计值d(m0)。

(4)增加嵌入维数使得m1＞m0，重复步骤(2)和(3)，直到相应的维数估计值d(m)不再随m的增长而在一定误差范围内变化为止。此时得到的d 即为吸引子的关联维数。如果d 随m的增长而增长，并不收敛于一个稳定的值，则可认为该系统是一个随机过程。

2.3 仿真实验

仿真分析时以经典的大气模型Lorenz 流混沌系统为例，如式所示。

式中，a=16，b=4，r=45.92，取x相分量生成混沌时间序列。

对所生成的混沌时间序列经量化、宽间隔处理后将得到能应用于实际跳频通信系统中的跳频序列。实际的量化方法有均匀量化法、余弦量化法、k维截断法、中间多比特抽取和排序法等，仿真时选择较为简单的均匀量化法。而宽间隔处理的方法有去中间频带法、对偶频带法、丢弃法、平移替代法和随机平移替代法，仿真时宽间隔处理法选用随机平移替代法。由此生成了混沌跳频序列，以供下面分析研究。

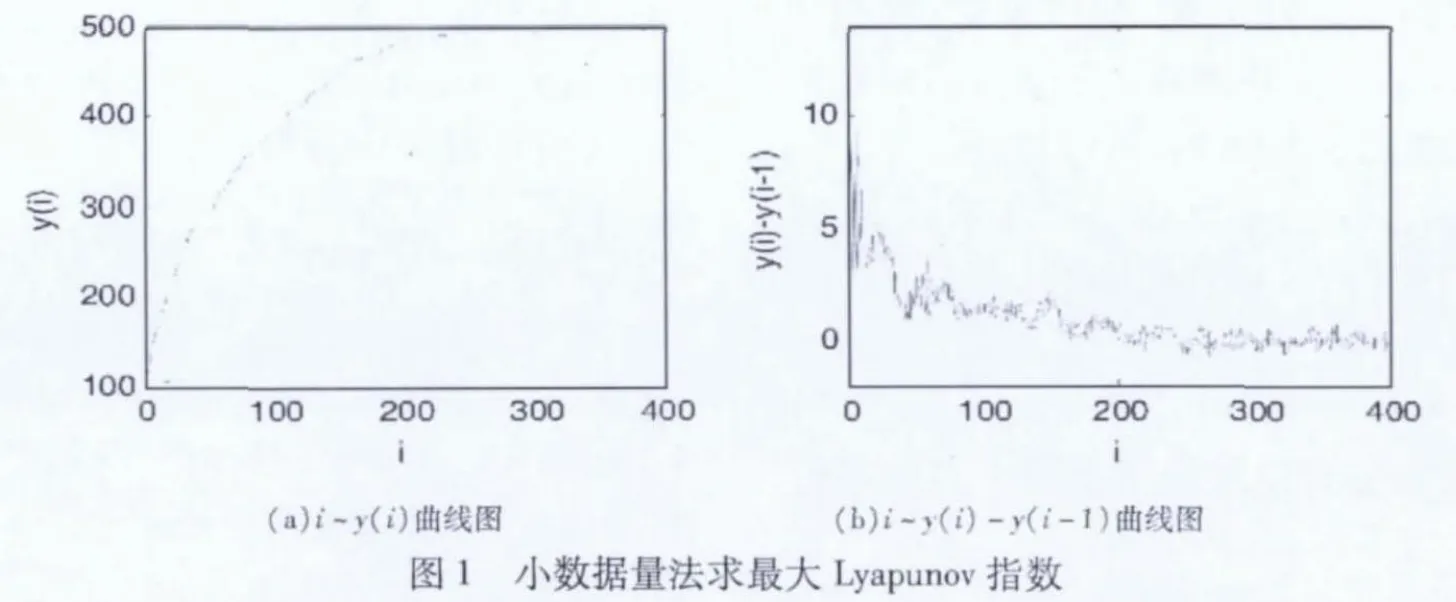
将混沌跳频序列前1 ×104个点去掉，取之后5000 点，利用小数据量算法，得到由Lorenz 流系统生成的混沌跳频序列的i～y(i)和i～y(i)－y(i－1)曲线如图1 所示。

对于图1(b)中的i～y(i)－y(i－1)曲线图，取未达到饱和之前的区域100～200 作为线性区间，继而可以得出图1(a)中i～y(i)曲线图中相应区域的斜率为1.0049，则该斜率对应最大Lyapunov 指数λ=1.0049 ＞0，是正值。

将混沌跳频序列前1 ×104个点去掉，取之后3000 点，利用G－P 算法，得到由Lorenz 流生成的混沌跳频序列的双对数曲线如图2(a)所示，嵌入维－关联维(m－D)曲线如图2(b)所示。

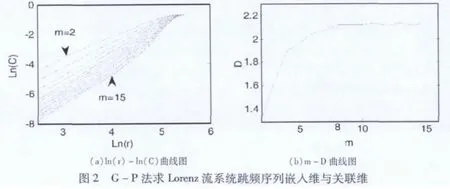
从图2(b)m－D 曲线图中可以看到，当m 取到8 之后关联维数D 大致不变，此时D≈2.119，是分数且有限。

从最大Lyapunov 指数和分形维数的分析中可看到，Lorenz 流系统生成的跳频序列的最大Lyapunov 指数是正值，而分形维数为非整数且有限，故而可知Lorenz 流系统生成的混沌跳频序列具有混沌性，继而可利用混沌理论对其分析。

3 相空间重构

从2.3 节中的分析中可知混沌跳频序列具有混沌性，因此可以利用混沌理论分析混沌跳频序列，而相空间重构是混沌理论分析的基础，故而本小节中主要研究分析混沌跳频序列的重构参量。现实中获得的是序列的观测值，对这些观测值进行相空间的重构分析可以得到与原混沌系统特性等价的相空间，通过分析该相空间有助于了解原系统的特性。对于混沌序列{x1，x2，...，xN}，重构相空间如式(1)所示，可看到相空间重构中重要的参量是时间延迟和嵌入维数。

3.1 时间延迟

对于时间延迟来说，如果时间延迟τ 太小，相空间矢量Xi的相邻延迟点间的差别较小，包含原系统中吸引子的信息量较少，而冗余信息太多，重构后的相空间轨迹得不到充分扩展，难以获得混沌系统的实际特性;如果时间延迟τ 太大，获得的噪声信息较多，使得轨迹相互分离，导致获得的信息基本不相关，也不能获得原混沌系统的实际特性。故而，必须选择合适的时间延迟才能有效的分析原混沌系统的特性。

此处选取互信息量算法［9］计算时间延迟。设离散变量X、Y，其状态数目分别为m、n，则平均自信息量即信息熵定义为:

其中，Pi是变量X 在状态i 出现的概率。变量X、Y的联合熵定义为:

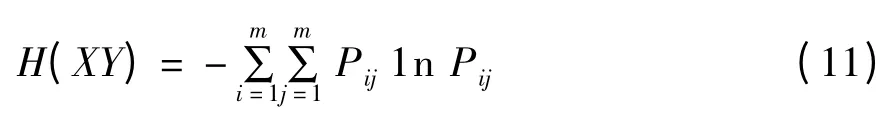
其中，Pij是变量X 在状态i 和变量Y 在状态j同时出现的概率，由此定义平均互信息量为:

对于一般情况，互信息为:

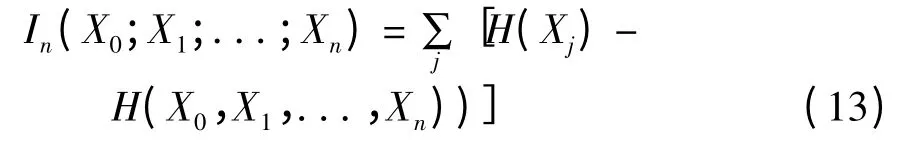
对于式(13)，I 第一次达到最小值的时间可作为相空间重构的时间延迟。

3.2 嵌入维数

对于嵌入维数来说，如果嵌入维数选择的太小，相空间在向低维投影时，会造成虚假交叉;如果嵌入维数太大，则得到的相空间中噪声太多而失去了原混沌系统的实际特性。在实际应用中，嵌入维数越大，重构得到的相空间中的噪声越大，系统中的重要信息被淹没，得到的信息大部分都是噪声，而且选择维数越大，计算的工作量也越大。故选择合适的嵌入维数是必要的。

分析时选择Cao 算法［10］分析混沌跳频序列的嵌入维数，Cao 算法的具体描述如下。定义:

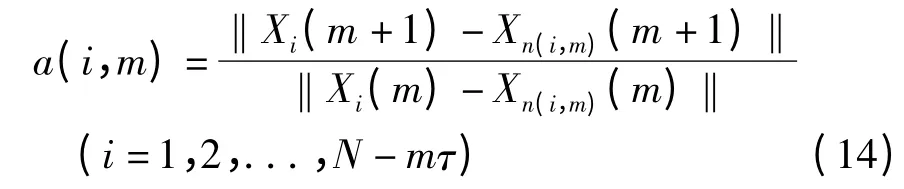
其中，‖·‖为范数，Xn(i，m)(m)是d 维空间中Xi(m)最近邻点。求a(i，m)的均值:

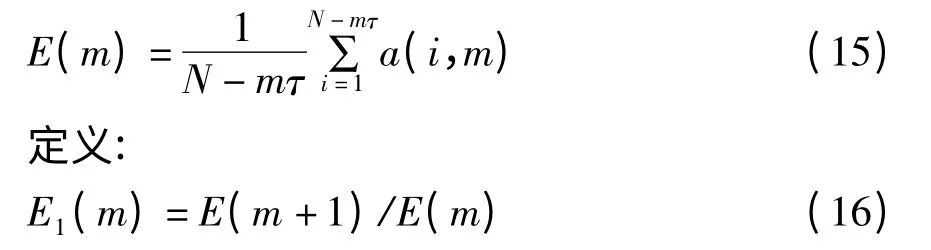
当m 大于某个值m0时，E1(m)不再变化。对于随机序列，理论上E1(m)应逐渐增加，但在实际中不容易判断有限长序列E1(m)到底是在缓慢增加还是已经停止变化。所以需要再附加一个条件:

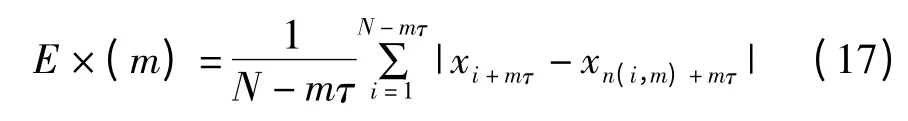
其中，n(i，m)的定义与上面相同。类似(16)式，定义:

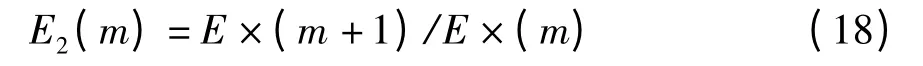
对于随机序列，序列数据间在理想情况下可认为没有相关性，则E2(m)将始终为1;但对于确定性序列，序列中的数据之间关系是与嵌入维数m 有关的，E2(m)不能始终为1。

3.3 仿真实验

图3是由互信息量法得到互信息量随时间变化的t～I 曲线图，分析时去掉前1 ×104个点，取其后的5000 点做分析。可见当t=3，互信息量第一次达到最小值，根据互信息量法可知时间延迟τ=3。

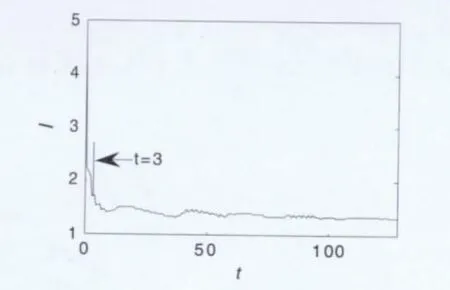
图3 互自相关法求时间延迟

图4是由Cao 算法求得的E1、E2随时间变化的曲线图，分析时去掉前1 ×104个点，取其后的3000个点做分析。从图中可以看到当d=4 之后，E1、E2基本不再随时间的变化而变化，则可得到嵌入维数m=4。

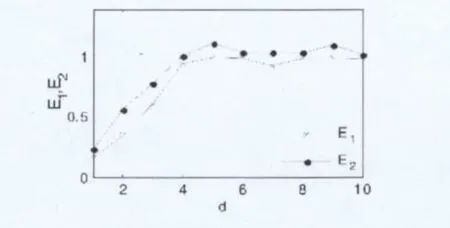
图4 Cao 算法求嵌入维数

图5 中，(a)图表示Lorenz 流x、y相的混沌跳频序列的相图，(b)图表示Lorenz 流x相的混沌跳频序列在时间延迟τ=3时的二维相空间重构图，(c)图表示Lorenz 流x相的混沌跳频序列在时间延迟τ=1时的二维相空间重构图，(d)图表示Lorenz流x相的混沌跳频序列在时间延迟τ=15时的二维相空间重构图。

从图5 中可以看到，由Lorenz 流生成的混沌跳频序列，时间延迟的选取对于它的相空间重构影响很大。合适的时间延迟τ(如图5(b)所示)可得到与原系统(如图5(a)所示)等价的相空间;τ 太小则混沌跳频序列的重构相空间轨迹在主对角线上压缩(如图5(c)所示)，不能极大的得到原混沌系统的信息;τ 太大则混沌跳频序列的重构相空间在轨迹上出现分离(如图5(d)所示)，使得延迟坐标间的相互信息丢失。

4 结束语

分析时首先利用混沌性判别理论研究混沌跳频序列的混沌性，以Lorenz 系统为例进行了验证分析，并得出Lorenz 系统生成的混沌跳频序列具有混沌性的结论。继而利用相空间重构理论对Lorenz流系统生成的混沌跳频序列分析了时间延迟和嵌入维数，在对时间延迟的分析中得到时间延迟的选取太大或太小都不能较好的得到原系统的特性，必须选择合适的时间延迟才能得到与原系统等价的系统。所研究内容从混沌领域的研究方向拓展了对混沌跳频序列的分析，有一定的研究意义和研究价值。

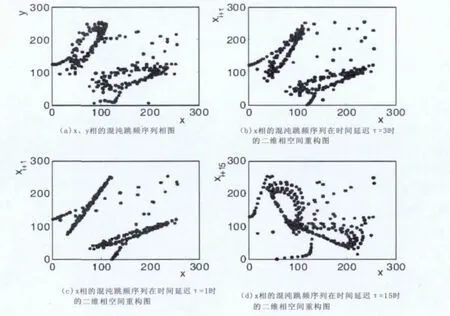
图5 Lorenz 流混沌系统二维相图

［1］Yang J，Hu L，Liu P，Zhou R.Design and Implementation of a New Kind of Chaotic Frequency Hopping Sequences［C］.International Conference on Wireless Communications，Networking and Mobile Computing.2008:1－4.

［2］米良，唐刚.一种混沌跳频序列构造方法［J］.通信学报，2005，26(12):69－74，80.

［3］Liu X D，He X Q，ANG X Y，Jiang N.A New Chaotic FH Sequences Generator based On Dynamic Quantization［J］.Journal of Communications and Information Sciences，2011，1:49－55.

［4］郭文洲.有界噪声激励下典型非线性系统的关联维数和Lyapunov 指数估计［D］.杭州:浙江大学，2006.

［5］张宇河，修春波，刘向东.相空间重构延迟时间与嵌入维数的选择［J］.北京理工大学学报，2003，23(2):219－224.

［6］林嘉宇.语音信号非线性分析与处理［D］.长沙:国防科学技术大学，1998.

［7］傅强，钟纪华，张朝曦.Rayleigh－Benard 对流温度信号的混沌特性分析［J］.解放军理工大学学报(自然科学版)，2011，12(5):536－540.

［8］党建武，黄建国.基于G.P 算法的关联维计算中参数取值的研究［J］.计算机应用研究，2004，(1):48－51.

［9］吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉:武汉大学出版社，2002.

［10］张淑清，贾健，高敏，韩叙.混沌时间序列重构相空间参数选取研究［J］.物理学报，2010，59(3):1576－1582.