李小飞，严证

（1.长江大学工程技术学院，湖北 荆州434020；2.茨城大学理学部，日本 茨城3108512）

0 引言

设A表示在单位圆盘U＝｛z：｜z｜＜1，z∈C｝内单叶解析且具有泰勒展开式：

的函数族.用K（γ）（0≤γ＜1）表示传统意义上的γ阶凸函数族，即

β－UCV（α）表示A中满足下面条件的函数f构成的函数族：

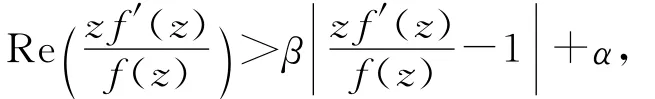
β－K（α）表示A中满足下面条件的函数f构成的函数族：

这里－1≤α≤1，β＞0.对此函数族及其特殊的函数族，近20年有很多作者进行过研究并得到了一些十分重要的结论.2010年，Breaz等［1］特别研究了函数族β－UCV（α）和β－K（α）的凸性.

2002年，Nishiwaki等［2］又提出了新的思想.设ρ＞1，用N（ρ）表示A中由满足下面不等式的函数组成的函数族：

N（ρ）的定义是有意义的，如取f（z）＝（1／（2ρ－1））｛1－（1－z）2ρ－1｝.特别地，当时，Uralegaddi等［3］对函数族N（ρ）的系数不等式等进行过研究，对于同形式的其他函数族，Nishiwaki等［4－6］做过相应的研究.用ND（α，β）表示A中由满足下面不等式的函数f（z）构成的函数族：

用MD（α，β）表示A中由满足下面不等式的函数f（z）构成的函数族：

这里α＞1，β≤0，z∈U.函数族ND（α，β）和MD（α，β）由Nishiwaki等［7］引入.对于此函数族，目前的文献并不多，且集中在基础性质的研究.

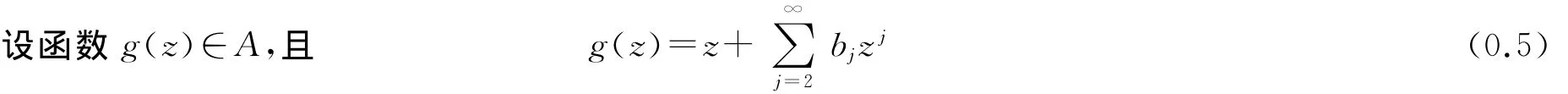
对于fi（z）∈A，γi＞0（i＝1，2，…，n），Breaz等［8－10］定义了积分算子函数Fn（z），Gn（z）和In（z）：

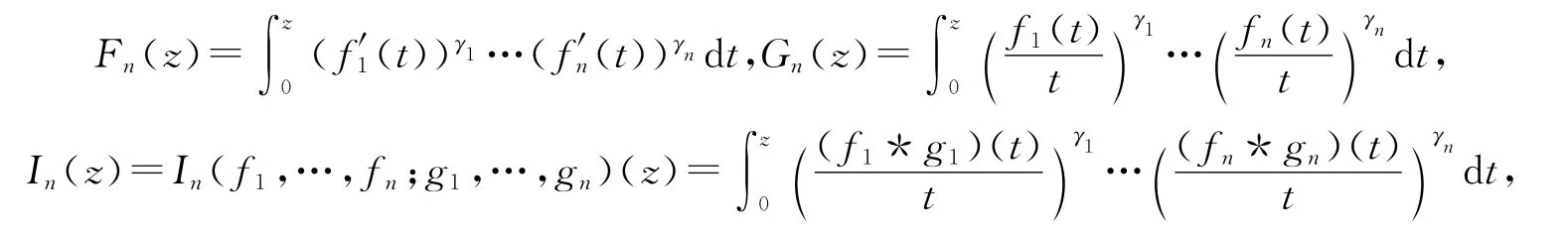
这里α＞1，β≤0，z∈U.本文中利用解析函数的性质和解不等式的技巧，研究函数族MDg（α，β）的系数不等式和函数族 ND（α，β）和 MD（α，β）中的积分算子函数Fn（z），Gn（z），In（z）的性质.

1 主要结果

定理1.1 若函数f（z）∈A 由（0.1）式定义，g（z）由（0.5）式定义，且满足下面不等式

则f（z）∈MDg（α，β），这里α＞1，β≤0，z∈U.

定理1.1的证明 为了方便，记cj＝ajbj.假设f（z）∈A 由（0.1）式定义，g（z）由（0.5）式定义，且不等式（1.1）式成立，即

现记

所以f（z）∈MDg（α，β）.定理得证.

定理1.2 若fi（z）∈ND（αi，βi），αi＞1，βi≤0（i＝1，2，…，n），则Fn（z）∈N（ρ），这里

定理1.2的证明 由Fn（z）的定义，得

利用条件（0.3）式，得

推论1.3 若fi（z）∈ND（α，β），α＞1，β≤0，则Fn（z）∈N（ρ），这里ρ＝1＋（α－1）

推论1.3的证明 在定理1.2中令α1＝α2＝…＝αn＝α，β1＝β2＝…＝βn＝β即可.

推论1.4 若f（z）∈ND（α，β），α＞1，β≤0，则 Fγ（z）∈N（ρ），这里ρ＝1＋（α－1）γ，Fγ（z）＝

定理1.5 若fi（z）∈MD（αi，βi），αi＞1，βi≤0（i＝1，2，…，n），则Gn（z）∈N（ρ），这里

定理1.5的证明 由Gn（z）的定义，得

利用条件（0.4）式，得

推论1.6 若fi（z）∈MD（α，β），α＞1，β≤0，则Gn（z）∈N（ρ），这里

推论1.6的证明 在定理1.5中令α1＝α2＝…＝αn＝α，β1＝β2＝…＝βn＝β即可.

推论1.7 若f（z）∈MD（α，β），α＞1，β≤0，则 Gγ（z）∈N（ρ），这里ρ＝1＋（α－1）γ，Gγ（z）＝

定理1.8 若fi（z）∈MDgi（αi，βi），αi＞1，βi≤0（i＝1，2，…，n），则In（z）∈N（ρ），这里

定理1.8的证明 由In（z）的定义，容易验证In（0）＝I′n（0）－1＝0，且

将（1.3）式变形，得

［1］Breaz N，Breaz D，Darus M.Convexity properties for some general integral operators on uniformly analytic functions classes［J］.Computers and Mathematics with Applications，2010，60：3105－3107.

［2］Nishwaki J，Owa S.Coefficient inequalities for certain analytic functions［J］.Int J Math Math Sci，2002，29（5）：285－290.

［3］Uralegaddi B A，Ganigi M D，Sarangi S M.Univalent functions with positive coefficients［J］.Tamkang J Math，1994，25（3），225－230.

［4］Nishiwaki J，Owa S.Coefficient inequalities for analytic functions［J］.Int J Math Sci，2002，29：285－290.

［5］Owa S，Nishiwaki J.Coefficient estimates for certain classes of analytic functions［J］.J Inequal Pure Appl Math，2002（3）：1－5.

［6］Uralegaddi B A，Ganigi M D，Sarangi S M.Univalent functions with positive coefficients［J］.Tamkang J Math，1994，25：225－230.

［7］Nishiwaki J，Owa S.Certain classes of analytic functions concerned with uniformly starlike and convex functions［J］.Applied Mathematics and Computation，2007，187：350－355.

［8］Breaz D，Owa S，Breaz N.A new integral univalent operator［J］.Acta Universitatis Apulensis，2008，16：11－16.

［9］Breaz D，Breaz N.Two integral operators［J］.Studia Universitatis Babes－Bolyai，Mathematica，Cluj－Napoca，2002（3）：13－21.

［10］Frasin B A.General integral operator defined by Hadamard product［J］.Matematicki Vesnik，2010，62（2）：127－136.

［11］Breaz N，Breaz D，Darus M.Convexity properties for some general integral operators on uniformly analytic functions classes［J］.Computers and Mathematics with Applications，2010，60：3105－3107.

［12］Breaz D.The integral operator on the SP（α，β）［J］.Acta Universitatis Apulensis，2008，16：17－22.

［13］Breaz D.A convexity property for an integral operator on the class UST（K，γ）［J］.Acta Universitatis Apulensis，2009，20：107－110.