Zhi-hong ZHANG*, Zhao-gang XU, Xiu-li DU, Hong-yan LI

The Key Laboratory of Urban Security and Disaster Engineering, Ministry of Education, Beijing University of Technology, Beijing 100124, P. R. China

Impact of consolidation pressure on contaminant migration in clay liner

Zhi-hong ZHANG*, Zhao-gang XU, Xiu-li DU, Hong-yan LI

The Key Laboratory of Urban Security and Disaster Engineering, Ministry of Education, Beijing University of Technology, Beijing 100124, P. R. China

Consolidation deformation occurs in clay liners under the self-weight of wastes at a simple garbage dump or dredged sediment dump, which leads to a decrease in the porosity. However, the migration of contaminants in clay liners is influenced by the porosity. Thus, the impact of consolidation deformation of clay liners on the migration of contaminants cannot be ignored. Based on Biot’s consolidation theory, the contaminant migration theory, and consideration of the three kinds of migration mechanisms of convection, diffusion, and adsorption, a one-dimensional migration model of contaminants in deforming porous media was established, and the finite difference method was adopted to obtain the numerical solutions for an established initial-boundary value problem. The impact of consolidation pressure on the migration law of a contaminant was studied. The results show that, regardless of adsorption modes, different consolidation pressures have similar impacts on the migration law of the contaminant. Namely, over a certain migration time, the greater the consolidation pressure is, the smaller the migration depth of the contaminant. The results also show that, while the migration time increases, the impact of a certain increment of consolidation pressure on the variation of contaminant concentration with the depth increases gradually and, while the migration depth increases, the impact of a certain increment of consolidation pressure on the variation of the contaminant concentration with time increases gradually.

clay liner; consolidation pressure; consolidation deformation; contaminant migration

1 Introduction

Natural clay layers are widely used as the liners at simple garbage dumps and dredged sediment dumps, without consideration of impermeable treatment or environmental protection. Compared with sanitary landfills, contaminants in leachate or in sediment penetrate through the clay liner more easily, and soil and groundwater may be polluted. Thus, this type of dump poses a high risk of secondary pollution to the surrounding environment. In addition, due to the large dump area, large dumped amount, and high absolute content of waste, as time passes on, if the clay liner is penetrated and leakage occurs, the influence on the surroundingenvironment lasts a long time and spreads over large areas. Therefore, it is of significance to study whether the contaminant will penetrate the liner and cause secondary pollution to the surrounding soil and groundwater over a certain time, which is related to the migration of the contaminants in the liner. When studying the migration of contaminants in a liner, soil is generally assumed to be a rigid porous media, without consideration of the impact of deformation of the liner on the contaminant migration (El-Zein 2008; Li and Cleall 2010), which cannot fully reflect the actual contaminant migration in the liner. On one hand, the contaminant migration in the liner is affected by multiple complex mechanisms, among which the convection and dispersion effects are directly related with soil porosity. On the other hand, due to the facts that the service life of these dumps is generally long and the dumped amount is huge, the clay liner will undergo time-dependent consolidation deformation under the self-weight of garbage or dredged sediment, leading to a decrease in the porosity, which is bound to affect the migration process of contaminants. Hence, when studying the migration of contaminants in the clay liner, the impact of consolidation deformation of the clay liner on the migration process of the contaminants cannot be ignored.

Studies on contaminant migration in deforming soil have been performed recently by some scholars. Smith (2000) developed a one-dimensional model of contaminant transport in a deforming porous medium based on the conservation of mass including both fluid and soil, and found that the deformation of soil had a great impact on the contaminant transport. Peters and Smith (2002) studied one-dimensional contaminant transport through a deforming porous medium based on the research of Smith (2000). Alshawabkeh et al. (2005) and Alshawabkeh and Rahbar (2006) studied one-dimensional solute transport in a capped sediment under consolidation based on Terzaghi’s consolidation theory, and found that consolidation accelerated the breakthrough of the solute to the overlying cap. Fox (2007a, 2007b) developed a model, coupled with large strain consolidation and solute transport, to study solute transport in soil with large deformation, and found that consolidation had a long-term impact on solute transport. Lee et al. (2009) and Lee and Fox (2009) studied consolidation-induced solute transport considering nonlinear non-equilibrium sorption, and found that consolidation-induced advection has an important contribution to solute transport. Lewis et al. (2009a, 2009b) developed a one-dimensional large deformation model of coupled mechanical consolidation and solute transport to study solute transport in deforming clay liners, and found that consolidation is capable of accelerating solute transport. Zhang et al. (2008) developed a one-dimensional model for contaminant transport combining Biot’s consolidation theory with contaminant transport theory, and an analytical solution of the model was obtained based on simplified conditions. It was found that consolidation had an important impact on contaminant transport. Huang et al. (2010) developed a contaminant transport model considering the influence of liner consolidation on transport coefficients to study the contaminant transport in a deforming liner, and found that the impact of consolidation on contaminant transport should beconsidered when consolidation pressure is high.

Based on the investigation of Zhang et al. (2008), a one-dimensional contaminant transport model coupling Biot’s consolidation theory with the contaminant migration theory was improved. Without any simplification in parameters of the model, a numerical solution for the model was achieved, and the impact of consolidation pressure on the migration of a contaminant was studied for different adsorption modes.

2 Model establishment

2.1 Basic assumptions

The basic assumptions of the migration model are as follows:

(1) The soil is in an isothermal condition.

(2) The soil is an isotropic, saturated, and linear elastic continuum with a small amount of deformation.

(3) The soil particles and pore water are incompressible.

(4) The consolidation deformation of soil caused by the self-weight of clay liners is not considered.

(5) Soil deformation and contaminant migration occur only in the vertical direction.

2.2 Biot’s one-dimensional consolidation model

The one-dimensional model of Biot’s consolidation theory, taking no account of body force, can be written as

whereGis the shear modulus of soil,νis Poisson’s ratio of soil,uis the excess pore water pressure,wis the displacement of soil in thezdirection, andzis the spatial coordinate taking downwards as positive.

There are two unknown parametersuandw, in the one-dimensional consolidation equation. Therefore, one more equation is needed to solve this problem. Due to the fact that pore water is incompressible, the continuity equation of water flow can be used during the soil consolidation process. Namely, the changing rates of water and the whole soil volume are equal in a representative elementary volume (REV). Thereby, the one-dimensional flow continuity equation can be written as

whereρwis the density of water;gis the gravitational acceleration;εzis the vertical strain of soil;kis the permeability coefficient of soil, which changes with the consolidation deformation; andtis time.

Applying the generalized Hooke’s law in Eqs. (1) and (2), one obtains

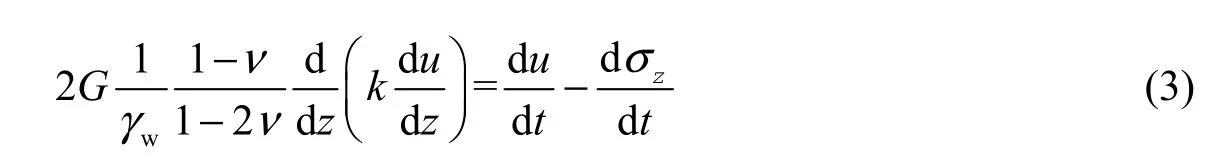
whereσzis the total stress of soil in thezdirection.

An empirical equation (Southeast University et al. 2005) related to the porosity ratio was adopted to describe the change law ofk, which can be defined as

wherek0is the initial permeability coefficient,eis the void ratio of soil,e0is the initial void ratio of soil, andckis the permeability index and is defined as 0.5e0.

As the pore water and soil particles are assumed to be incompressible, the changed soil volume is equal to the changed pore volume during the consolidation process. Th us, the computational equations of porosity and the void ratio can be expressed, respectively, as follows:

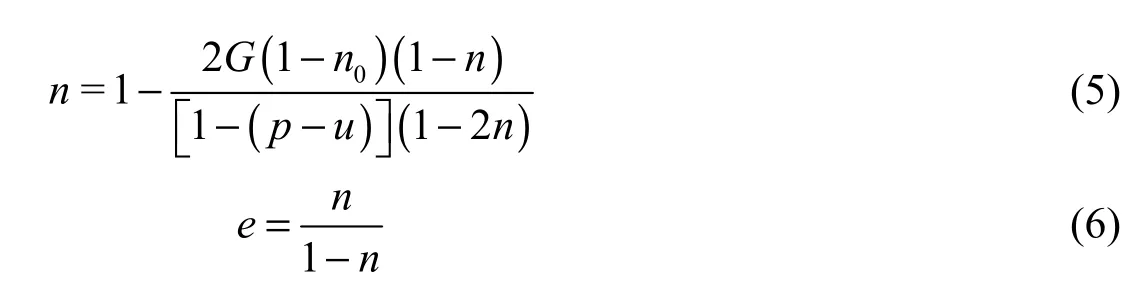
wherenis the porosity of soil,n0is the initial porosity, andpis the consolidation pressure on the clay liner.

2.3 One-dimensional migration model of contaminant in deforming porous media

While contaminants migrate in soil, a portion of the contaminants are adsorbed on the soil skeleton, and this portion of the contaminants moves together with the soil particles during the soil consolidation compression process; other contaminants move alon g with the pore water. Based on the mass conservation law of contaminants in the liquid phase and in the solid phase, and only taking account of convection, diffusion, and adsorption mechanisms, a one-dimensional migration model of contaminants in deforming porous media was established in the space coordinates, as follows:

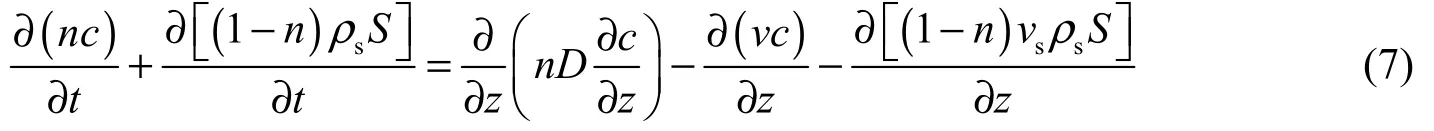
wherecis the concentration of a contaminant in pore water;ρsis the density of soil particles;Sis the adsorption concentration on the soil skeleton, which reflects the adsorption properties of soil particles for the contaminant and can be described by the adsorption equation;vis the Darcy seepage speed;vsis the velocity of the soil skeleton; andDis the hydrodynamic dispersion coefficient, composed of the effective molecular diffusion coefficient and the mechanical diffusion coefficient, and can be obtained from Eqs. (8), (9), and (10):

whereDeis the effective molecular diffusion coefficient;DLis the mechanical dispersion coefficient;D0is the free diffusion coefficient in an open water body;vtis the actual seepage speed of pore water;αLis the vertical dispersity, whose value is generally in the range of 0.1 cm to 5 m in indoor tests (Wang 2008); andτis the tortuosity factor of the porous media, related to the pore properties of soil, and can be defined by porosity asτ=nm, wheremis an empirical parameter (Liu et al. 2004).

Compared with the conventional contaminant migration equation, the novelty of Eq. (7) is the introduction of the term describing the movement of contaminants adsorbed by soil particles. Biot’s consolidation equation and the contaminant migration equation are linked by this term and parameters affected by consolidation deformation, and, thus, the consolidation equation and the migration equation are coupled. Because of consolidation deformation, the parameters such as the porosity, the Darcy seepage speed, the velocity of the soil skeleton, and the hydrodynamic dispersion coefficient, are variable.

2.4 Definite conditions

To obtain the numerical solution of Eq. (7), the following assumptions were established for the model:

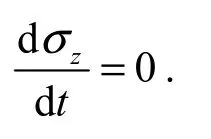
(2) The soil layer discharges water from the upper surface.

(3) The concentration of contamination sourcec0is a constant and does not change with time.

(4) The background contaminant concentration in the soil layer is not taken into consideration.

The definite conditions of the model can be obtained as follows from the above assumptions:

For the consolidation equation:

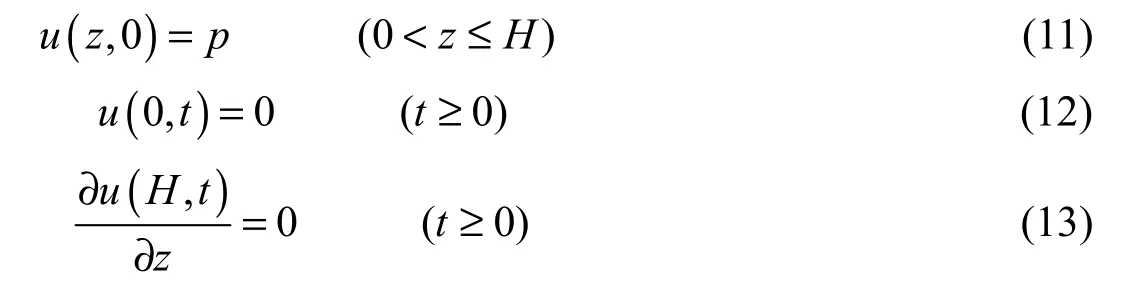
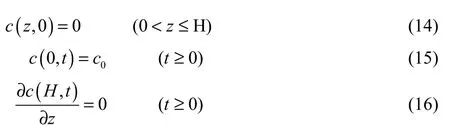
For the migration equation:whereHis the thickness of the soil layer. Combined with the definite conditions, Eq. (11) through (16), a numerical solution for Eqs. (1), (2), and (7) can be worked out with the finite difference method. The migration law of the contaminant can be obtained with consideration of the small deformation of soil.

3 Results and discussion

3.1 Parameter values

Ammonia nitrogen was selected as the simulated contaminant. The concentration of the contamination source wasc0=500 mg/L and the free diffusion coefficient of ammonia nitrogen in the open water body was=1.76× 10−9m2/s. The studied soil layer is a natural clay layer whose thickness isH= 2 m, initial void ratio ise0=0.8, initial permeability coefficient iscm/s, density of soil particles is, Poisson’s ratio isν=0.3, shear modulus isG=2.6× 103kPa, empirical parameter ism= 2.5, and vertical dispersity isαL= 0.001 m.

The program Matlab was used to obtain the solution of the migration model, and the effects of the consolidation pressure on the temporal and spatial distribution of the ammonia nitrogen concentration in the clay liner were studied for different adsorption modes.

3.2 Results of numerical calculation and discussion

Three adsorption modes were considered to describe the adsorption property of soil particles: the linear adsorption mode, Freundlich adsorption mode, and Langmuir adsorption mode. The equations of different adsorption modes and the values of adsorption parameters are shown in Table 1.

Table 1 Adsorption modes and main parameters

3.2.1 Impact of consolidation pressure on variation of contaminant concentration with depth

As shown in Figs. 1, 2, and 3, regardless of the kinds of adsorption modes, for the specific migration years, the greater the consolidation pressure is, the smaller the migration depth of the contaminant in the soil. It is also shown in the figures that the frontal surface of the contaminant concentration shifts toward the left when the consolidation pressure increases. The contaminant concentration values on the frontal surfaces at a certain depth decrease with the increase of consolidation pressure. At the same time, it can also be observed that along with the increase of the migration time, the contaminant concentration frontal surfacescorresponding to different consolidation pressures become sparse, which shows that the impact of a certain increment of the consolidation pressure on contaminant migration increases gradually with the migration time. In other words, the increment of the corresponding migration depth under a certain increment of consolidation pressure is increasingly large with the migration time. In addition, regardless of the kinds of adsorption isotherm equations applied, the migration depth of the contaminant will increase gradually with the increase of migration time under the effect of a certain consolidation pressure.

The phenomenon that the migration depth and contaminant concentration at a certain depth decrease as the consolidation pressure increases is due to different compressed volumes of soil under different consolidation pressures, which result in different impact of consolidation pressures on the migration of the contaminant. During the compression process of soil under consolidation pressure, pore water is discharged and porosity decreases, which narrows the migration channel of the contaminant, reduces the permeability, weakens the convection and diffusion effects, and retards the migration of the contaminant. In addition, the greater the consolidation pressure is, the greater the amount of soil compression deformation and reduction of porosity, and the stronger the retardation of the contaminant migration, so the migration depth and contaminant concentration at a certain depth are smaller when the consolidation pressure is greater.

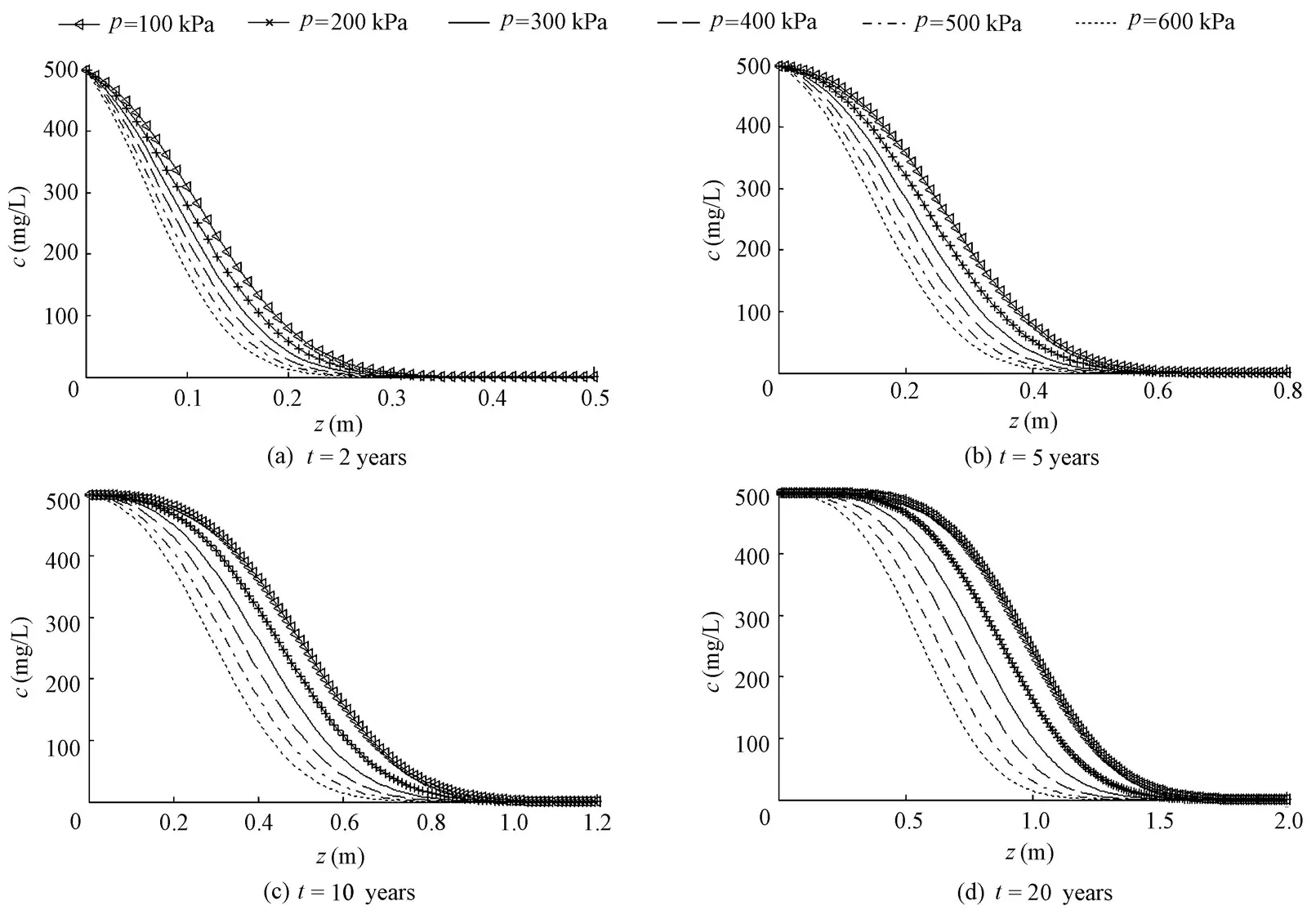
Fig. 1 Variation of contaminant concentration with depth at different consolidation pressures for linear adsorption

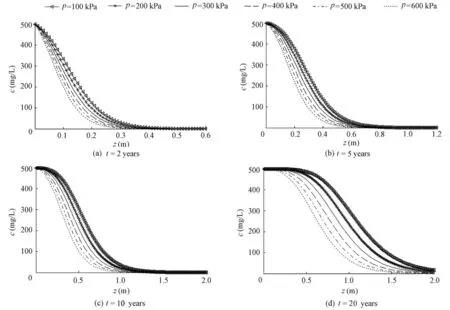
Fig. 2 Variation of contaminant concentration with depth at different consolidation pressures for Freundlich adsorption

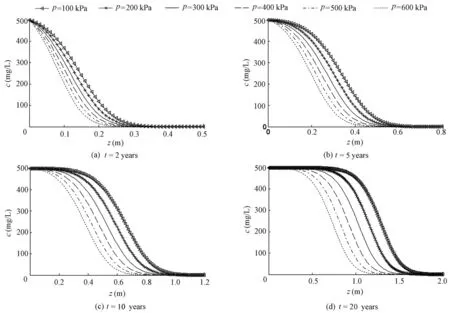
Fig. 3 Variation of contaminant concentration with depth at different consolidation pressures for Langmuir adsorption

3.2.2 Impact of consolidation pressure on variation of contaminant concentration with time

As shown in Figs. 4, 5, and 6, regardless of the kinds of adsorption modes, the impacts of consolidation pressure on the variation of contaminant concentration with time are similar. That is, for any depth profile in the clay liner, the contaminant concentration increases as time goes on under different consolidation pressures, until it finally reaches the value that is equal to the contamination source. The closer to the contamination source the depth profile is, the faster the contaminant concentration accumulates, and the more quickly the contaminant concentration will reach a value that is equal to that of the contamination source. In other words, the contaminant concentration at a depth profile that is far away from the contaminant source accumulates more slowly. However, as long as the migration time is long enough, with a constant concentration of the contamination source and a continuous supply, the concentration value will also eventually reach a value equal to that of the contamination source. For any depth profile studied, at a fixed time, the concentration on the frontal surfaces corresponding to different consolidation pressures decreases as the consolidation pressure increases. At the same time, it can be observed that the contaminant concentration frontal surfaces corresponding to different consolidation pressures gradually become sparse when the migration depth increases, which means that with the increase of the depth, the impact of a certain increment of consolidation pressure on the variation of the contaminant concentrationwith time increases gradually. In addition, no matter what the adsorption mode is, for a certain consolidation pressure, as the depth studied increases, the frontal surface of the contaminant concentration gradually becomes gentle, and the farther the depth profile is away from the contamination source, the more obvious this trend is.

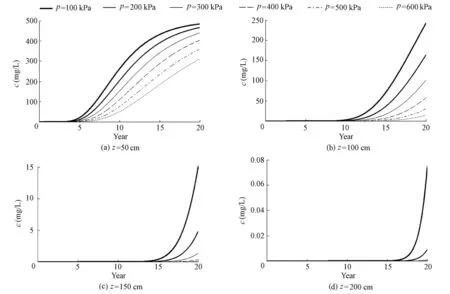
Fig. 4 Variation of contaminant concentration with time under different consolidation pressures for linear adsorption

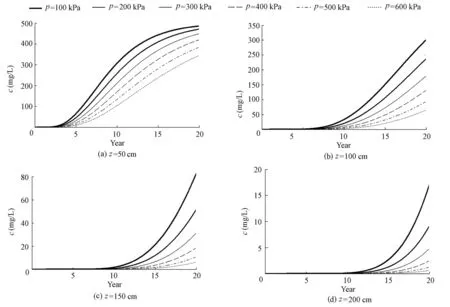
Fig. 5 Variation of contaminant concentration with time under different consolidation pressures for Freundlich adsorption

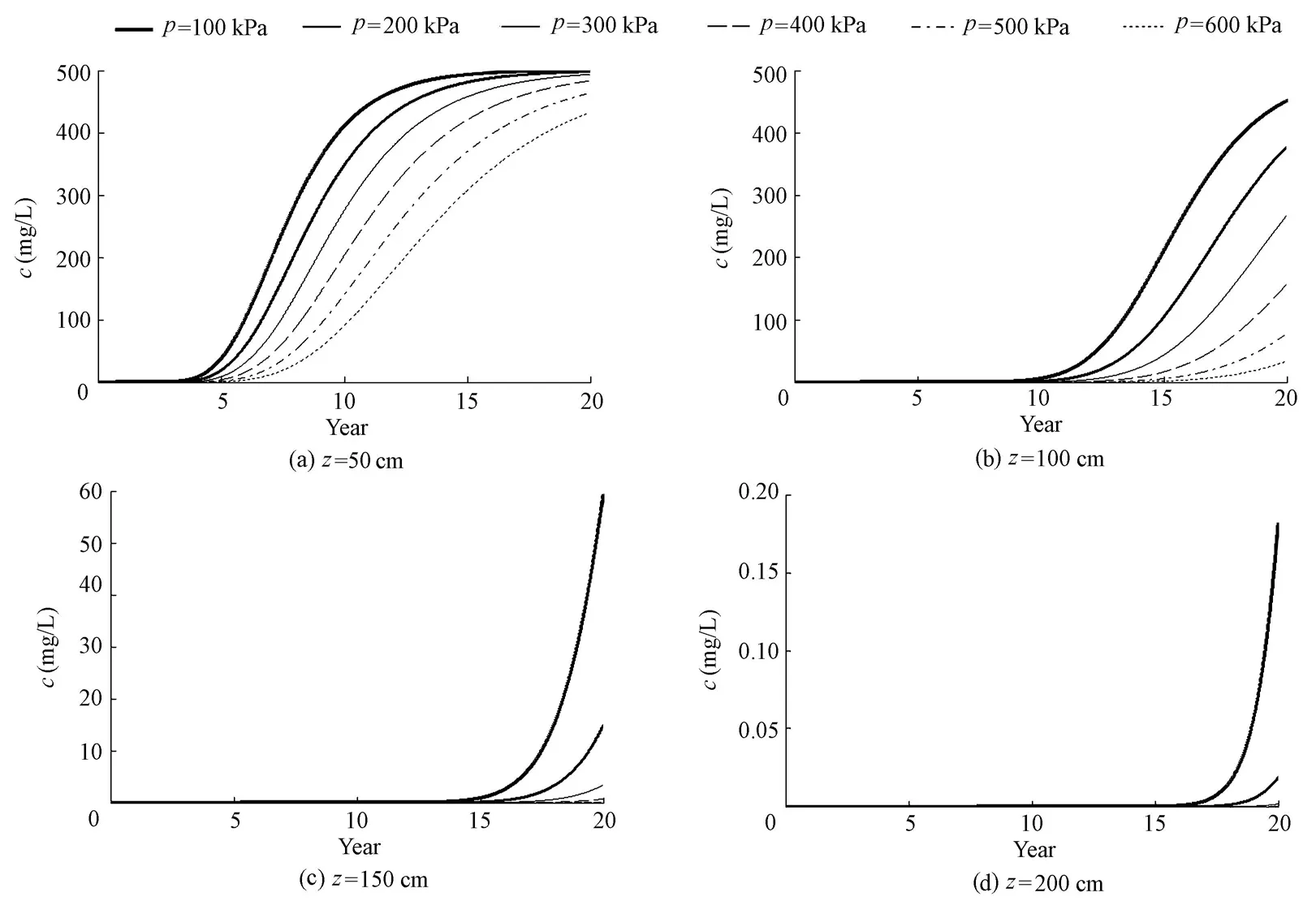
Fig. 6 Variation of contaminant concentration with time under different consolidation pressures for Langmuir adsorption

The reason that the concentration values on the frontal surfaces corresponding to different consolidation pressures at a fixed time decrease as the consolidation pressure increases is that the greater the consolidation pressure is, the greater the amount of deformation of soil and the porosity reduction, and the slower the contaminant migrates, resulting in less contaminant accumulation at a certain depth profile, and thus a lower concentration in the same migration time when the consolidation pressure is higher.

3.2.3 Contaminant migration depth at different consolidation pressures

The main purposes of studying the contaminant migration in a clay liner are to judge whether the contaminant would penetrate through the clay liner in a certain migration period, to provide a scientific basis for risk assessment of landfills or dredged sediment dumps, and to carry out a final evaluation to investigate the risk of secondary pollution to the surrounding environment and the groundwater.

According toQuality Standard for Ground Water(GB/T14848-93) of China, potable water must meet the standard requirements of Class III, in which the concentration of ammonia nitrogen should be no more than 0.2 mg/L. If this value is set as a standard for different adsorption modes, the migration depth of ammonia nitrogen at different times and under different consolidation pressures from Figs 1, 2, and 3 can be determined.

For both the linear adsorption and Langmuir adsorption, within 20 years, the contaminant concentration at the bottom of the investigated soil layer did not exceed the standard value. The relation curves of the migration depths versus consolidation pressures at different migration times are shown in Fig. 7. However, for the Freundlich adsorption, the contaminant concentration at the bottom of the investigated soil layer at the migration time of 20 years already exceeded the standard value, and the relation curve of the contaminant concentration at the bottom of the soil layer under different consolidation pressures can be seen in Fig. 8.

As shown in Fig. 7, regardless of the modes of adsorption, the migration depths of contaminants at different migration times decreased when the consolidation pressure increased, and there was a satisfactory linear relation between the migration depth and the consolidation pressure. The relational expressions and correlation coefficients are shown in Table 2. For the Freundlich adsorption, the contaminant concentration at the bottom of the investigated soil layer at the migration time of 20 years already exceeded the standard value, so the relation curve of the contaminant migration depth and consolidation pressure at the migration time of 20 years is not given for this mode.

As shown in Fig. 8, for the Freundlich adsorption, the contaminant concentration at the bottom of the investigated soil layer decreased while the consolidation pressure increased atthe migration time of 20 years; they were in an exponential relation, where the relational expression can be written asc=35.04e−0.001pand the correlation coefficient wasR=0.998. The contaminant concentration at the bottom of the investigated soil layer under any consolidation pressure at the migration time of 20 years can be obtained through this fitting formula.

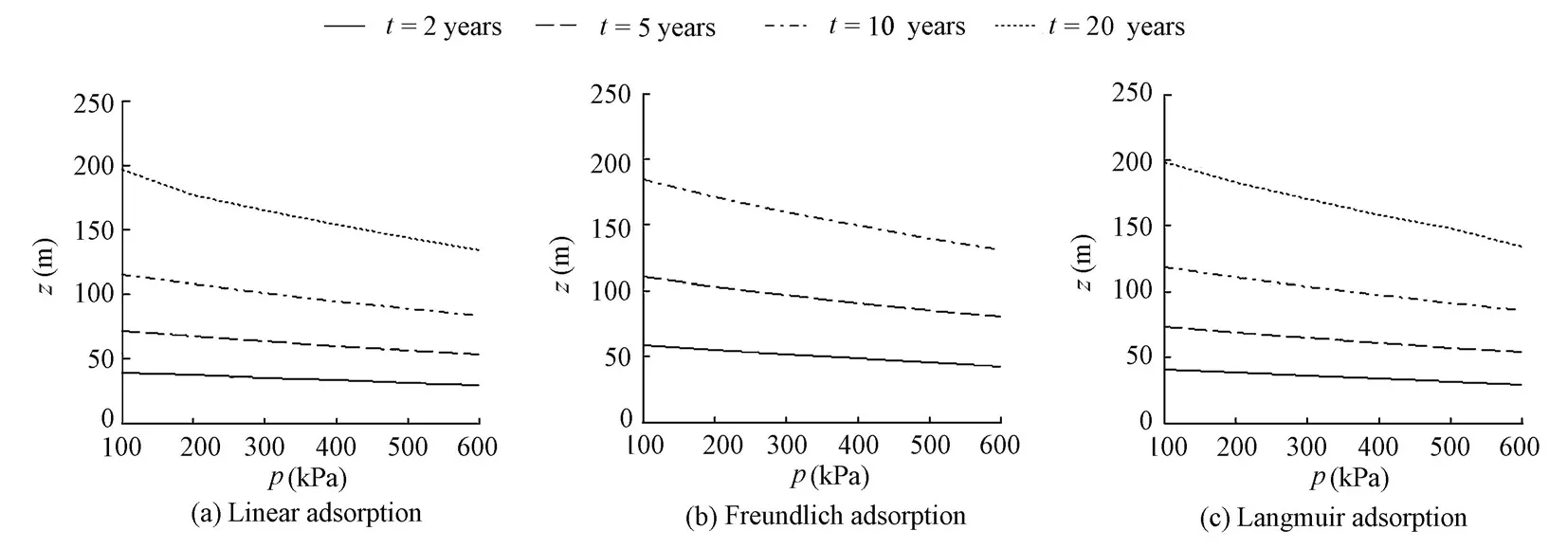
Fig. 7 Relation curves of contaminant migration depth versus consolidation pressure at different times for different adsorptions

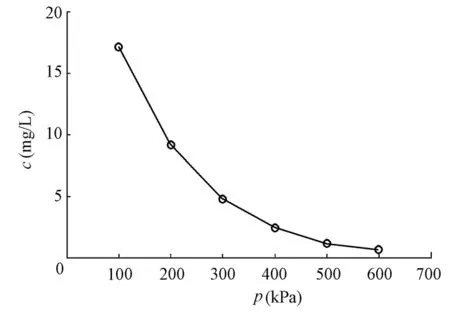
Fig. 8 Relation curve of contaminant concentration at bottom of soil layer versus consolidation pressure at migration time of 20 years for Freundlich adsorption

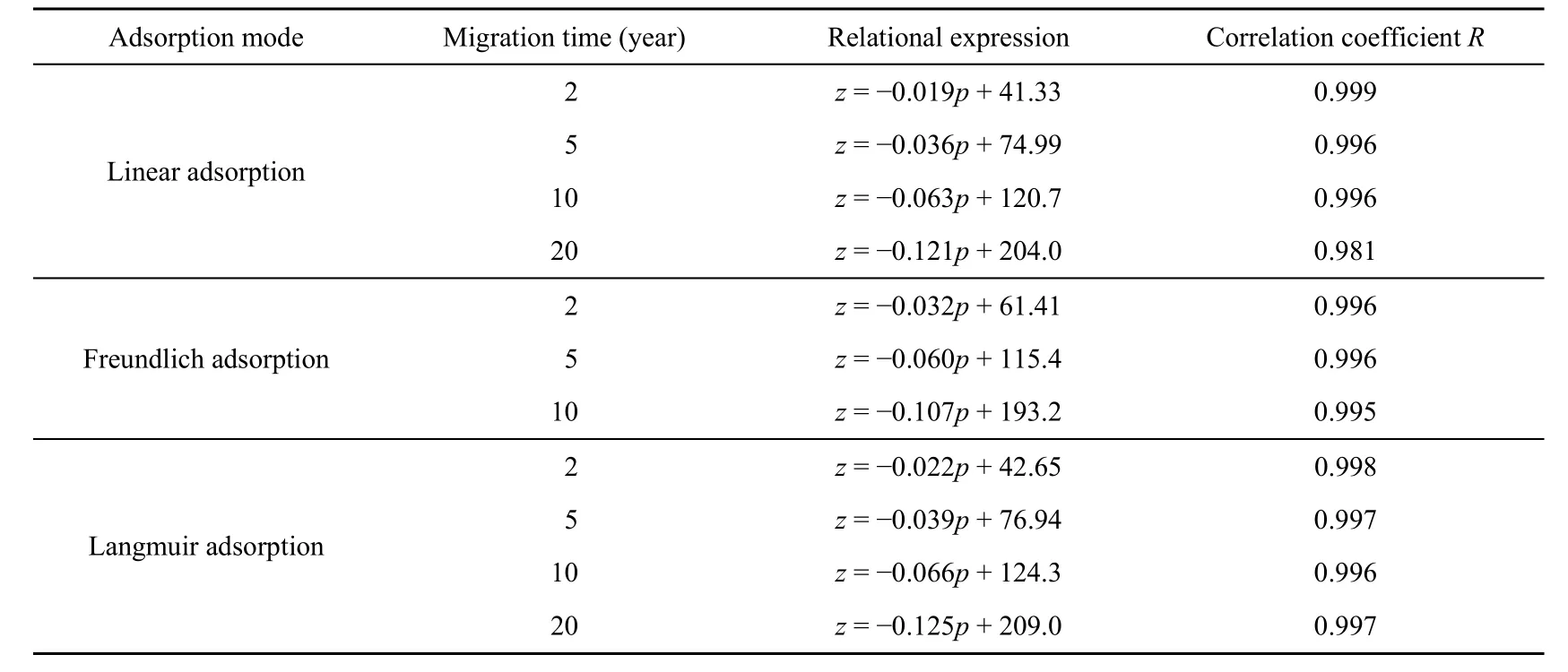
Table 2 Fitted formulas of migration depth and consolidation pressure

4 Conclusions

Because of the movement of the contaminant adsorbed to soil particles and parameters affected by consolidation deformation, Biot’s consolidation theory and contaminant migration theory were coupled to establish a migration model of contaminants in deforming porous media. The numerical solution for the established model was obtained with the finite difference method. The impact of consolidation pressure on the migration law of the contaminant for different adsorption modes was studied. From this study, the following conclusions can be obtained:

(1) The migration depths of the contaminant under different consolidation pressures were compared and analyzed. The results show that regardless of the adsorption modes, the greater the consolidation pressure is, the lesser the migration depth and the weaker the penetration ability of the contaminant. The reason is that the greater the consolidation pressure is, the more compacted the soil layer and the weaker the convection diffusion effect, and thus, the lesser the migration depth of the contaminant at the same migration time.

(2) The consolidation pressure had a direct impact on the accumulation velocity of the contaminant at any depth profile. The greater the consolidation pressure is, the slower the concentration accumulates, which results in a low concentration of contaminants at the same migration time.

(3) The variation curve shapes of the contaminant concentration with depth under different consolidation pressures are similar, and so are the variation curves of contaminants with time, which shows that there is no intrinsic impact of the variation of consolidation pressure on the migration law of the contaminant, but there is an impact on the migration speed of the contaminant. This impact will increase gradually as migration time goes on.

(4) Generally, a basically linear relationship is shown between the migration depth of the contaminant and consolidation pressure for all the three adsorption modes.

Alshawabkeh, A. N., Rahbar, N., and Sheahan, T. 2005. A model for contaminant mass flux in capped sediment under consolidation.Journal of Contaminant Hydrology, 78(3), 147-165. [doi:10.1061/j. jconhyd.2005.05.003]

Alshawabkeh, A. N., and Rahbar, N. 2006. Parametric study of one-dimensional solute transport in deformable porous media.Journal of Geotechnical and Geoenvironmental Engineering, 132(8), 1001-1010. [doi:10.1061/(ASCE)1090-0241(2006)132:8(1001)]

El-Zein, A. 2008. A general approach to the modelling of contaminant transport through composite landfill liners with intact or leaking geomembranes.International Journal for Numerical and Analytical Methods in Geomechanics, 32(3), 265-287. [doi:10.1002/nag.626]

Fox, P. J. 2007a. Coupled large strain consolidation and solute transport, I: Model development.Journal of Geotechnical and Geoenvironmental Engineering, 133(1), 3-15. [doi:10.1061/(ASCE)1090-0241(2007) 133:1(3)]

Fox, P. J. 2007b. Coupled large strain consolidation and solute transport, II: Model verification and simulation results.Journal of Geotechnical and Geoenvironmental Engineering, 133(1), 16-29. [doi:10.1061/ (ASCE)1090-0241(2007)133:1(16)]

Huang, L., Zhao, C. G., Zhang, X. D., and Liu, Y. 2010. 3D contaminant migration model with consolidation dependent transport coefficients.Chinese Journal of Geotechnical Engineering, 32(3), 420-427. (in Chinese)

Lee, J., and Fox, P. J. 2009. Investigation of consolidation-induced solute transport, II: Experimental and numerical results.Journal of Geotechnical and Geoenvironmental Engineering, 135(9), 1239-1253. [doi: 10.1061/(ASCE)GT.1943-5606.0000048]

Lee, J., Fox, P. J., and Lenhart, J. J. 2009. Investigation of consolidation-induced solute transport, I: Effect of consolidation on transport parameters.Journal of Geotechnical and Geoenvironmental Engineering, 135(9), 1228-1238. [doi:10.1061/(ASCE)GT.1943-5606.0000047]

Lewis, T. W., Pivonka, P., Fityus, S. G., and Smith, D. W. 2009a. Parametric sensitivity analysis of coupled mechanical consolidation and contaminant transport through clay barriers.Computers and Geotechnics, 36(1-2), 31-40. [doi:10.1061/j.compgeo.2008.04.003]

Lewis, T. W., Pivonka, P., and Smith, D. W. 2009b. Theoretical investigation of the effects of consolidation on contaminant transport through clay barriers.International Journal for Numerical and Analytical Methods in Geomechanics, 33(1), 95-116. [doi:10.1002/nag.708]

Li, Y. C., and Cleall, P. J. 2010. Analytical solutions for contaminant diffusion in double-layered porous media.Journal of Geotechnical and Geoenvironmental Engineering, 136(11), 1542-1554. [doi:10.1002/nag.903]

Liu, J. G., Wang, H. T., and Nie, Y. F. 2004. Fractal model for predicting effective diffusion coefficient of solute in porous media.Advances in Water Science, 15(4), 458-462. (in Chinese)

Peters, G. P., and Smith, D. W. 2002. Solute transport through a deforming porous medium.International Journal for Numerical and Analytical Methods in Geomechanics, 26(7), 683-717. [doi:10.1002/nag.219]

Smith, D. W. 2000. One-dimensional contaminant transport through a deforming porous medium: Theory and a solution for a quasi-steady-state problem.International Journal for Numerical and Analytical Methods in Geomechanics, 24(8), 693-722. [doi:10.1002/1096-9853(200007)24:8＜693::AID-NAG91＞3.0.CO;2-E]

Southeast University, Zhejiang University, Hunan University, and Suzhou University of Science and Technology. 2005.Soil Mechanics. Beijing: China Architecture and Building Press. (in Chinese)

Wang, H. T. 2008.Dynamics of Fluid Flow and Contaminant Transport in Porous Media. Beijing: Higher Education Press. (in Chinese)

Zhang, Z. H., Li T., Zhao, C. G., Yu, Y., and Tang, B. R. 2008. Model of contamination transport considering consolidation deformation of soils.Rock and Soil Mechanics, 29(6), 1435-1439. (in Chinese)

(Edited by Yun-li YU)

This work was supported by the National Natural Science Foundation of China (Grant No. 51008008).

*Corresponding author (e-mail:zhangzh2002@bjut.edu.cn)

May 21, 2012; accepted Oct. 12, 2012