NYAMORADI N.,SHEKARBIGI M.,RAZLANSARI A. and YAVARI M.

Department of Mathematics,Faculty of Sciences,Razi University,

67149 Kermanshah,Iran.

The Nehari Manifold and Application to a Quasilinear Elliptic Equation with Multiple Hardy-Type Terms

NYAMORADI N.∗,SHEKARBIGI M.,RAZLANSARI A. and YAVARI M.

Department of Mathematics,Faculty of Sciences,Razi University,

67149 Kermanshah,Iran.

Received 14 April 2012;Accepted 19 April 2013Abstract.In this paper,by using the Nehari manifold and variational methods,we study the existence and multiplicity of positive solutions for a multi-singular quasilinear elliptic problem with critical growth terms in bounded domains.We prove that the equation has at least two positive solutions when the parameters λ belongs to a certain subset of R.

AMS Subject Classifications:35A15,35B33,35J70

Chinese Library Classifications:O175.25

Nehari manifold;quasilinear elliptic equation;Sobolev critical exponent.

1 Introduction

In this paper,we consider the following quasilinear elliptic problem

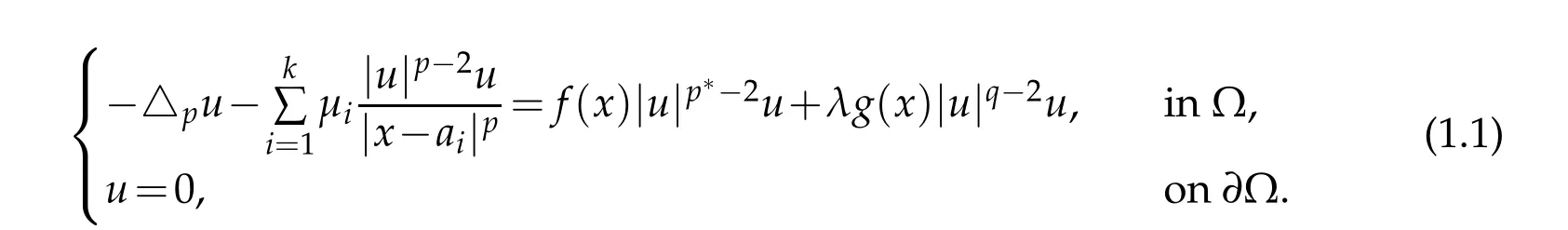
Problem(1.1)is related to the following Hardy inequality[1–3]:

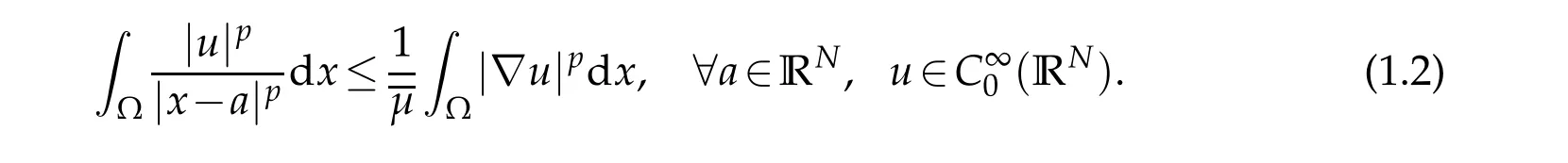
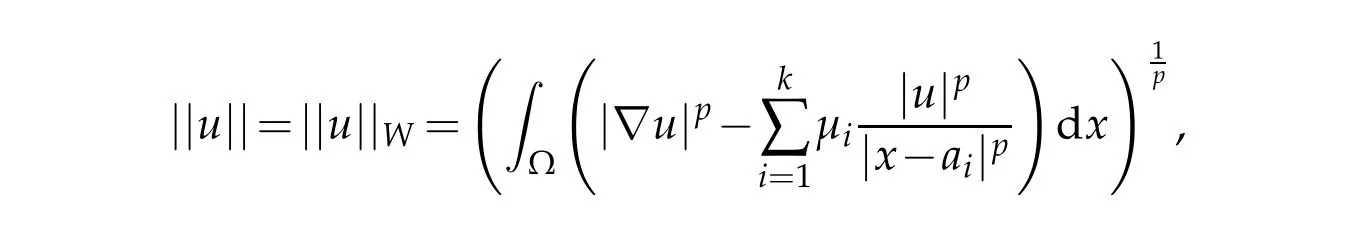
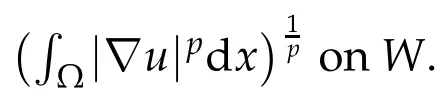
Definition 1.1.We say that u∈W is weak solution to(1.1)if for all v∈W we have

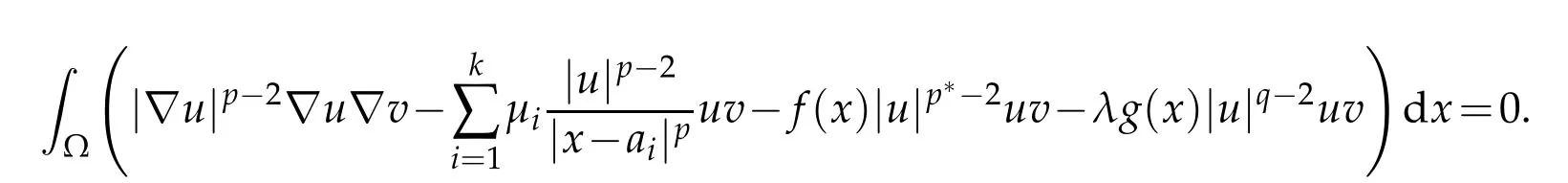
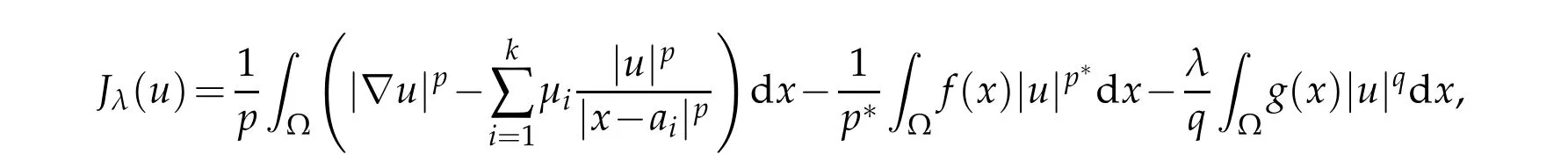
for every u∈W.

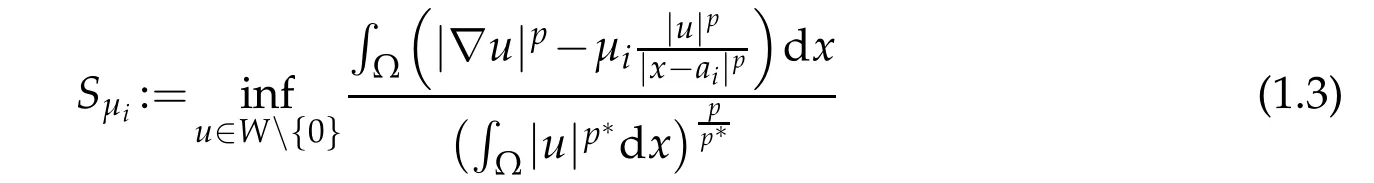
and from[4],we get that Sµiis independent of Ω.

In[5],the authors studied the following limiting problem:

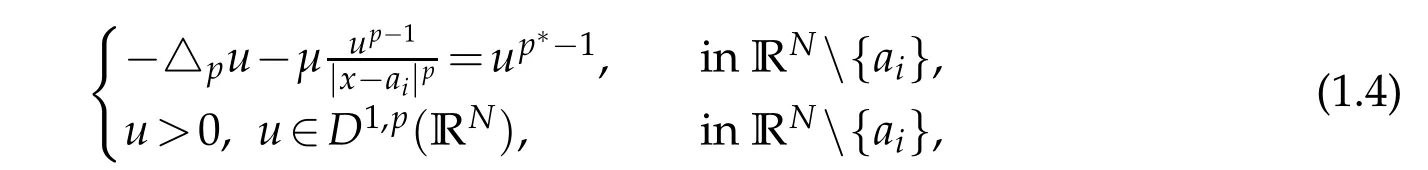
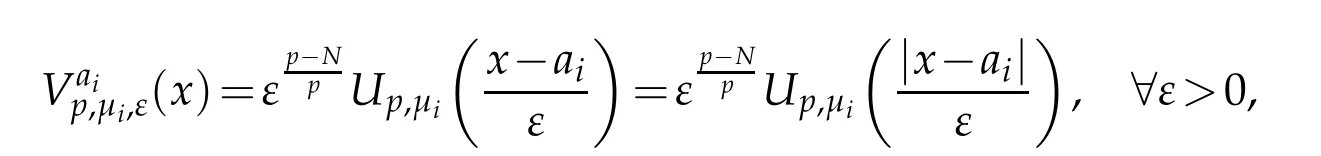
that satisfy

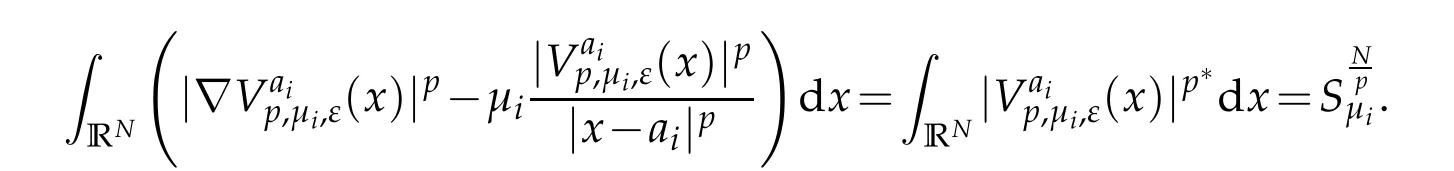
Moreover,the positive radial function Up,µihave the following properties:

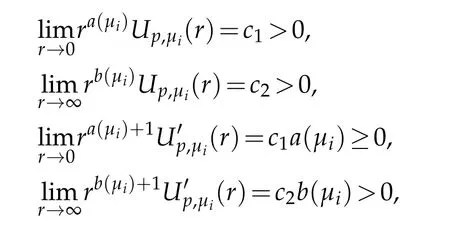
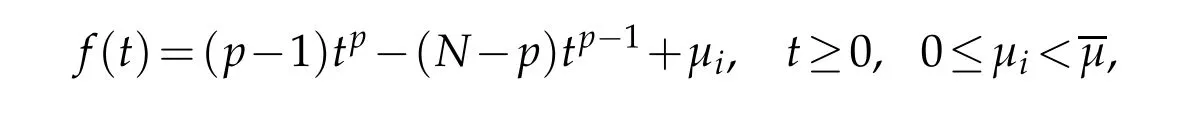
satisfying

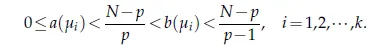
Thus

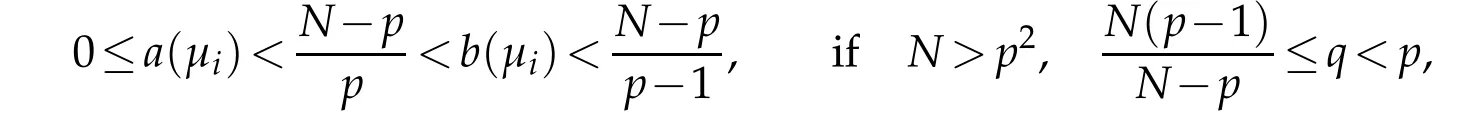
we have

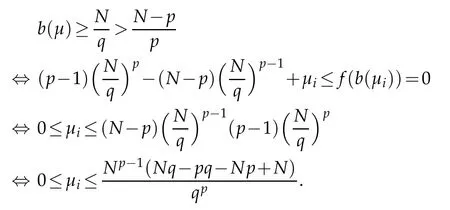
The above results are crucial to the study of problem(1.1).For example,in[6],by using mountain pass Theorem,Cao and Kang studied the problem(1.1)when 1＜p＜N,p≤q＜p∗,g=1.

In[7],by using Morse iteration,the authors studied the asymptotic behavior of solutions for Eq.(1.1);using critical point theory,the authors also proved the existence ofnontrivial solutions,when p=2,f≡1,g≡0.On the other hand,the author in[8]also studied Eq.(1.1),for p=2,f≡1,g≡0;they discussed the corresponding Rayleigh quotient and gave both sufficient and necessary conditions on the masses and locations of singularities for the minimum to be achieved.

In this paper,we will prove that there exists Λ＞0 such that(1.1)has at least two positive solutions for all λ∈(0,Λ).

The following assumptions are used in this paper:

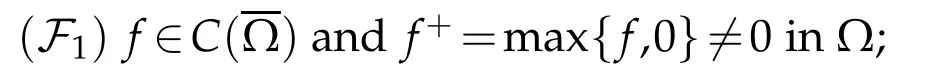
(F2)there exists an l,1≤l≤k such that

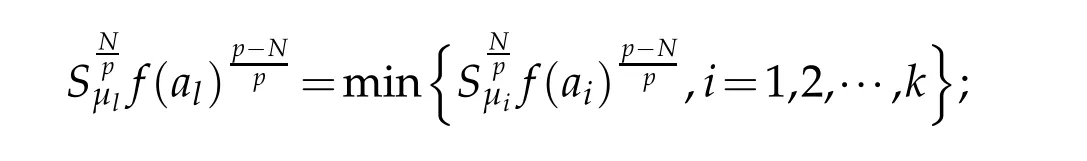
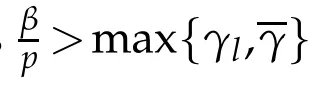
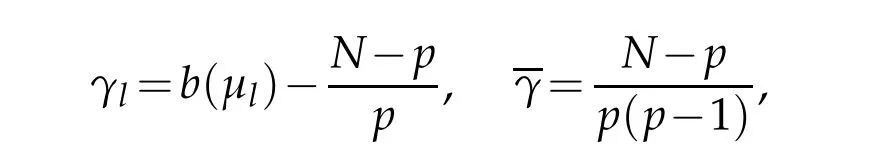
and

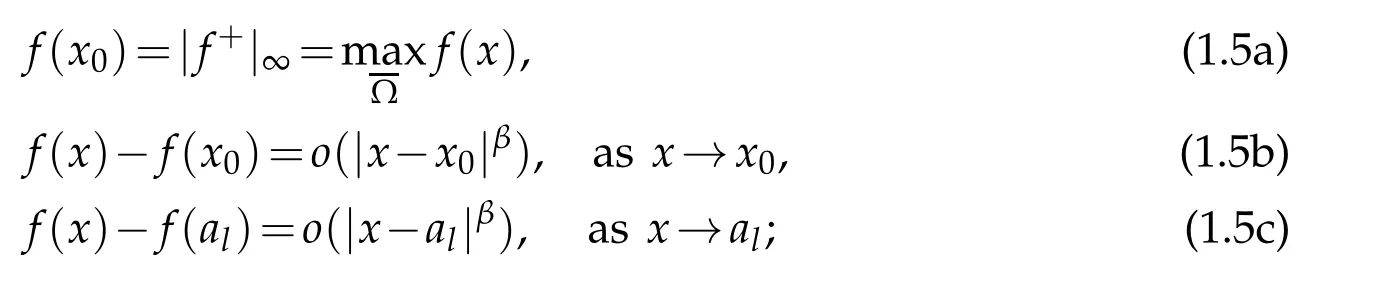
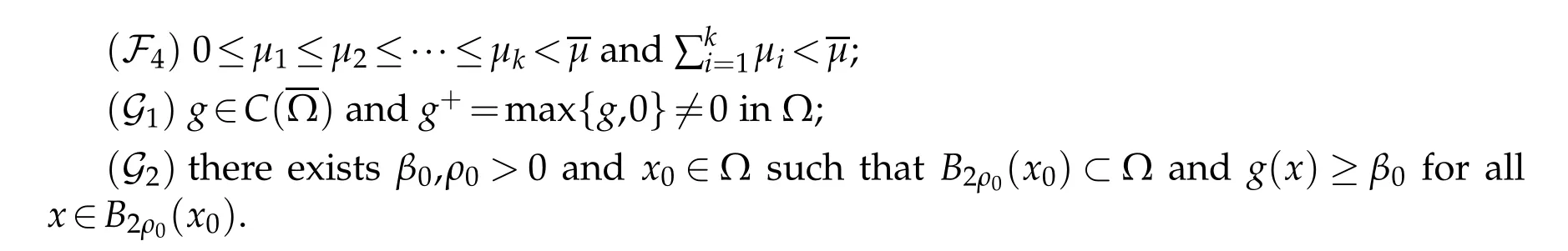
We define the following constant:

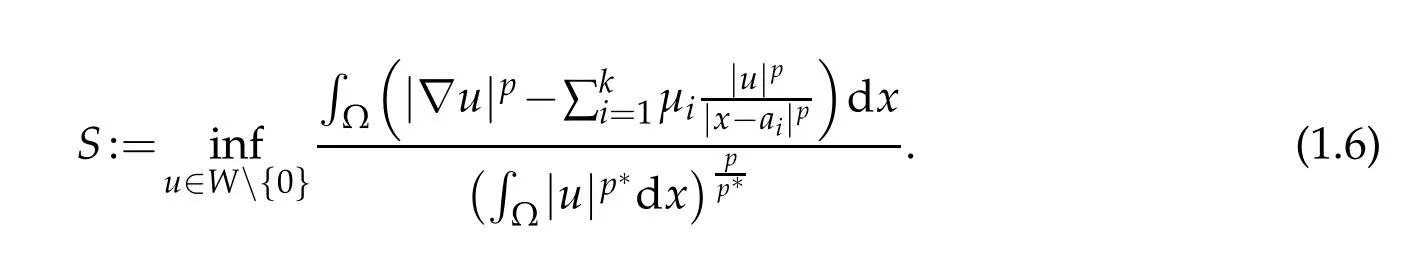
Let|Ω|be the Lebesgue measure of Ω and set

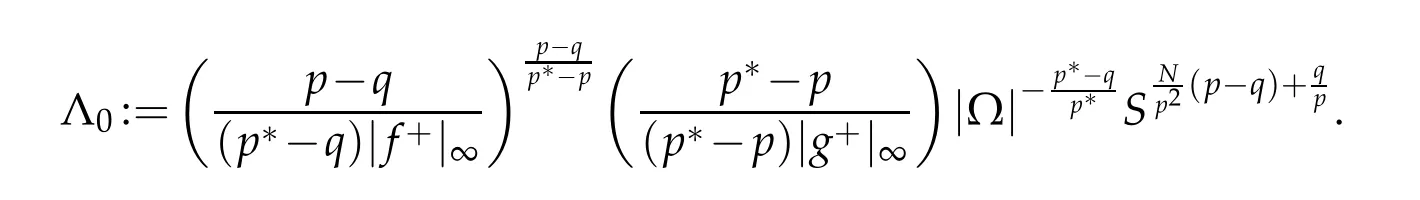
We are now ready to state our main results.

Theorem 1.1.Assume that(F1)−(F4)and(G1)−(G2)hold.If λ∈(0,Λ0)then problem(1.1) has at lest one positive solution.

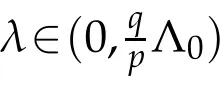
Remark 1.1.In[6],Cao and Kang considered problem(1.1)for 1＜p＜N,p≤q＜p∗and f=g≡1.Via variational methods,they proved the existence of positive solution of(1.1) when parameters p,q,λ,µiwith i=1,2,···,k and k≥2 satisfy suitable conditions.But the existence of positive solutions for(1.1)for 1≤q＜p＜N is not considered.Thus,we will complement the result found there.

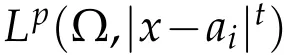
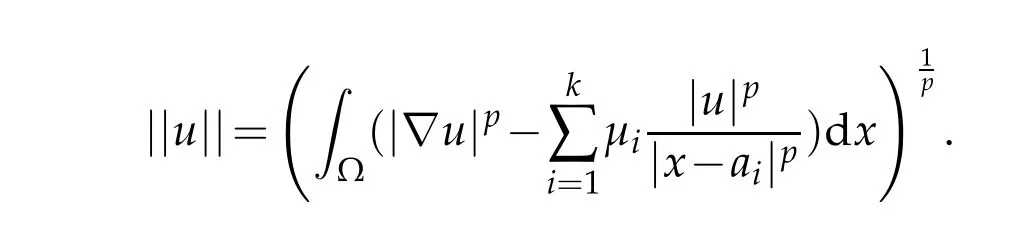
It is well known that the weak solutions of(1.1)are the critical points of the energy functional Jλ.If Jλis bounded below and that has a minimizer on W,then this minimizer is a critical point of Jλ.So,it is a solutionof thecorrespondingelliptic equation.However, the energy functional Jλ,is not bounded below on the whole space W,but is bounded on an appropriate subset,that is called Nehari manifold.

This paperis organized as follows:InSection2,wegive somepropertiesoftheNehari manifold.In Sections 3 and 4,we prove Theorems 1.1 and 1.2,respectively.

2 Nehari manifold

In this section,we will give some properties of Nehari manifold.As the energy functional Jλis not bonded below on W,it is useful to consider the functional on the Nehari manifold

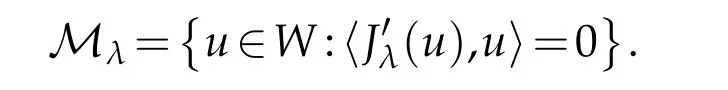
Thus that u∈Mλif and only if

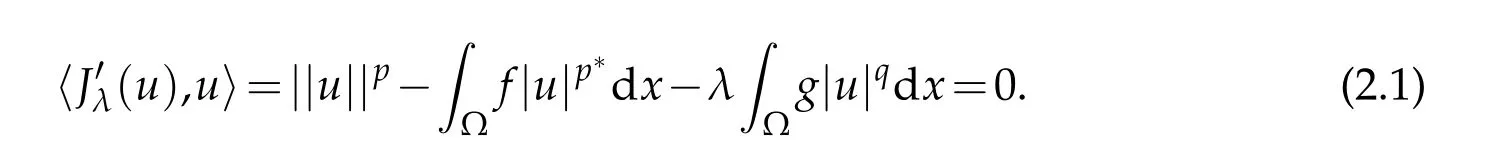
Note thatMλcontains every non-zero solution of Eq.(1.1).

Lemma 2.1.The energy functional Jλis coercive and bounded below onMλ.

Proof.Suppose u∈Mλ.From(1.6)and(2.1),the Holder inequality and embedding theorem it follows that

Since 1≤q＜p hence Jλis coercive and bounded below onMλ.

The Nehari manifold is closely linked to the behavior of the function of the form ψu:t→Jλ(tu)for t＞0.Such maps are known as fibering maps and introduced by Brown and Zhang[9]and are also discussed in[10].If u∈W,we have

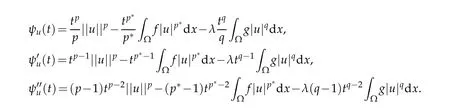
It is easy to see that

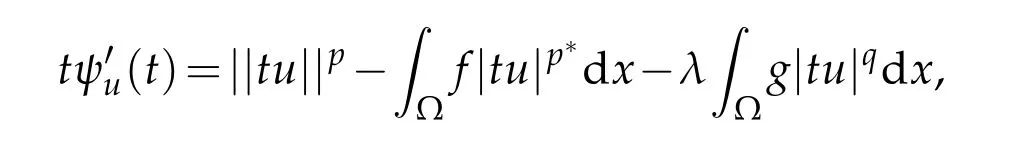
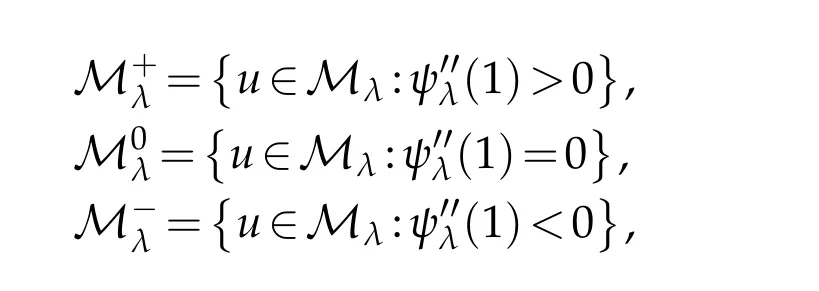
and note that if u∈Mλ,that isthen

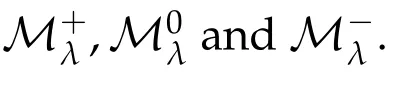
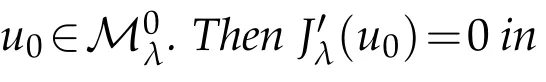
Proof.If u0is a local minimizer for JλonMλ,then u0is a solution of the optimization problem

Hence,by the theory of Lagrange multipliers,there exists Λ∈R such that

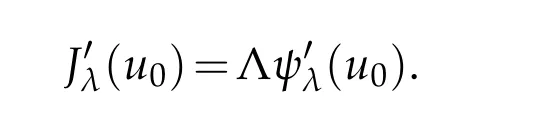
Thus,

Moreover,we have the following results.

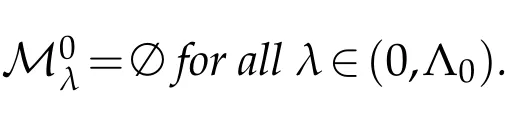
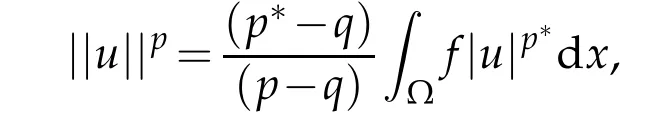
and

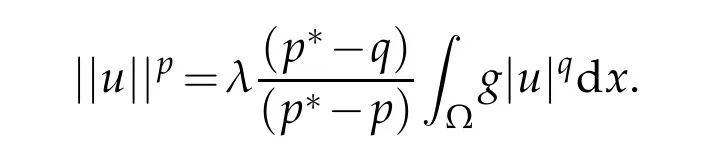
By(1.6)and(2.3),the H¨older inequality and the Sobolev embedding theorem,one can get

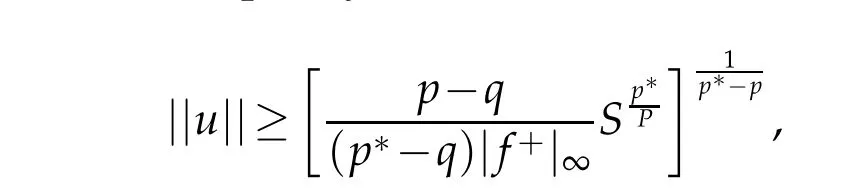
and also

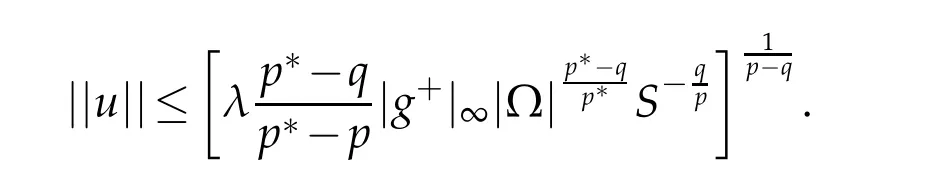
This implies that

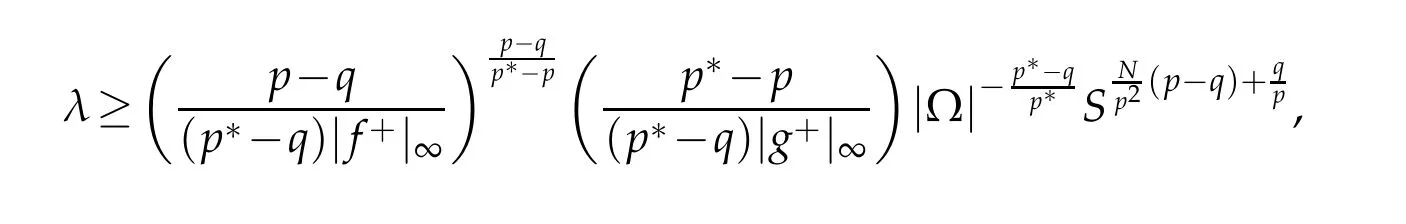
which is a contradiction.

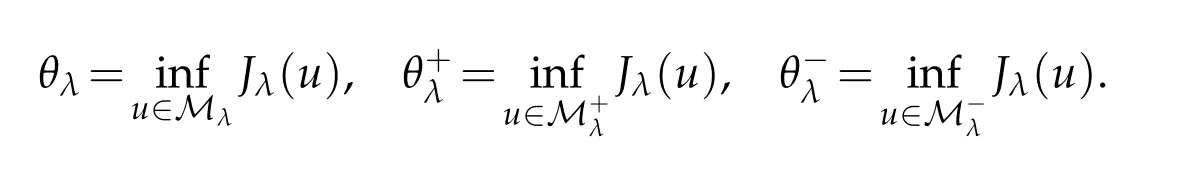
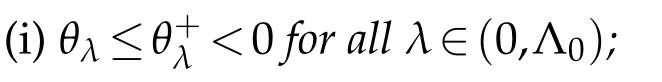
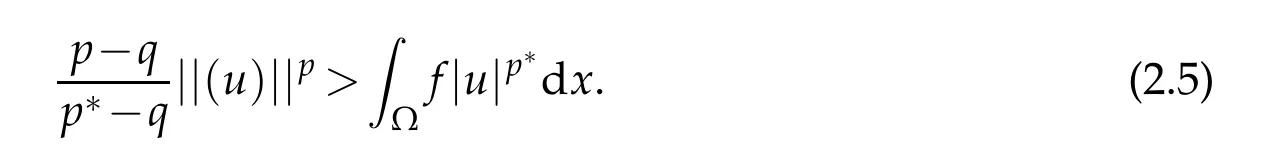
According to(2.1)and(2.5),we have

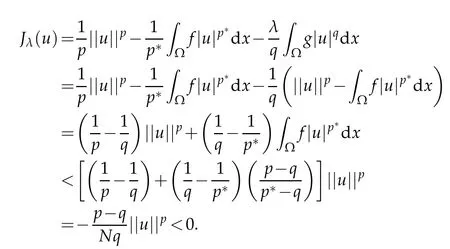
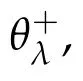
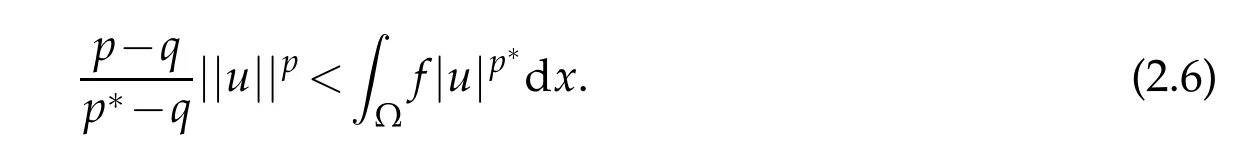
Moreover,by(F1)and(1.6),we have

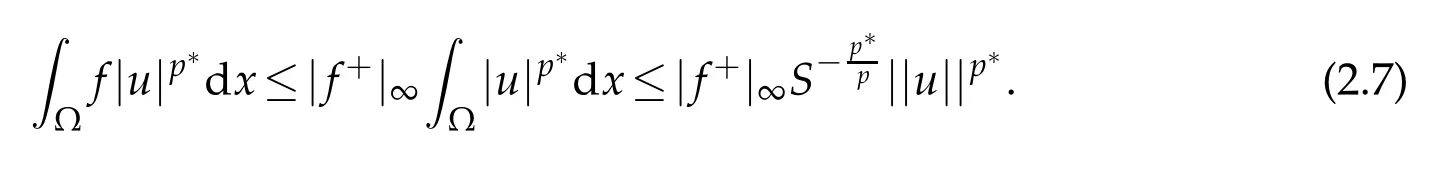
From(2.6)and(2.7),one can get

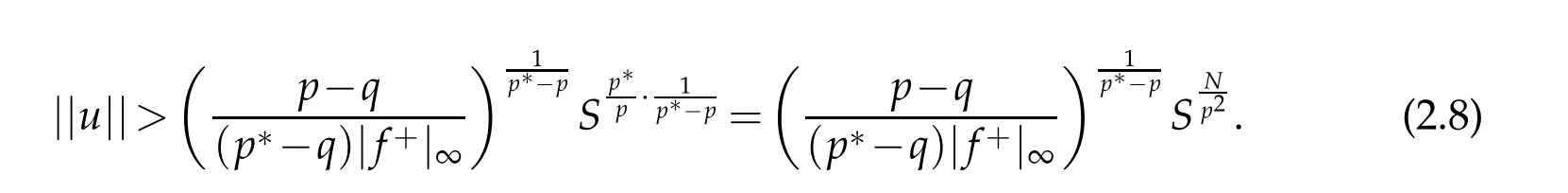
By(2.2)in proof of Lemma 2.1,we have

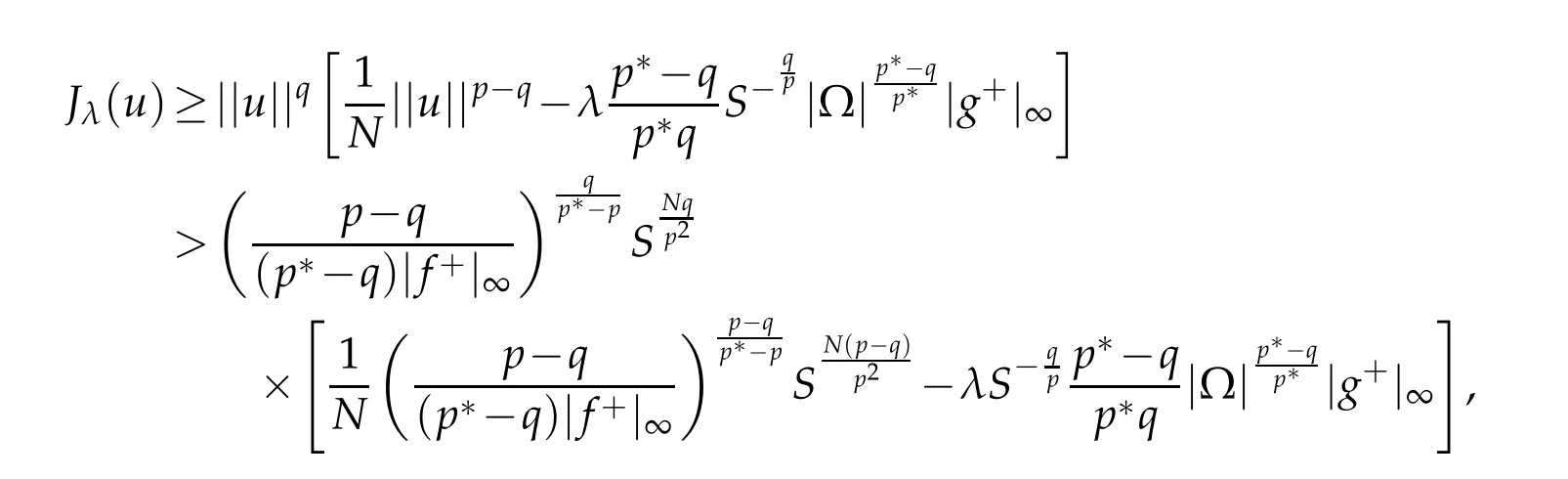
which implies that

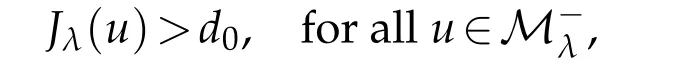
where d0=d0(q,N,|f+|∞,|g+|∞,S,λ,|Ω|)＞0.This completes the proof.

In order to get a better understanding of the Nehari manifold and fibering maps,we consider the function ϕu:R+→R defined by

Clearly,tu∈Mλ,if and only if ϕu(t)=λRΩg|u|qdx.Moreover,

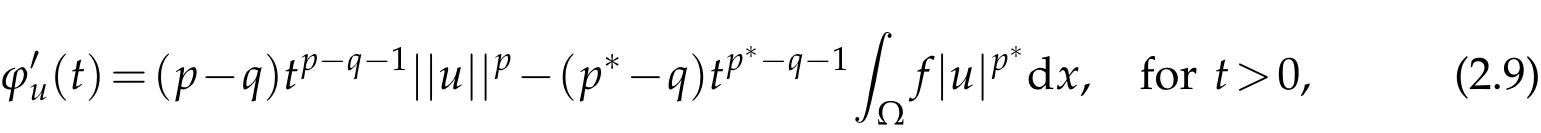
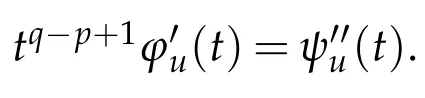
where

and clearly ϕuis strictly increasing on(0,tmax(u))and decreasing on(tmax(u),∞)with limt→∞ϕu(t)=−∞.Moreover,if λ∈(0,Λ0),then

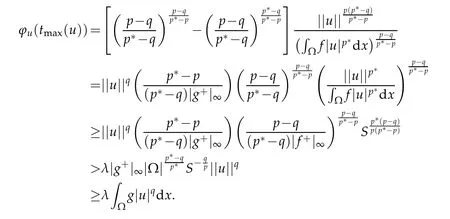
Therefore,we have the following lemma.

Lemma 2.5.Let λ∈(0,Λ0)and u∈W is a function satisfyingRΩf|u|p∗dx＞0.

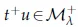
and ψuis decreasing on(0,t+),increasing on(t+,t−)and decreasing on(t−,∞). Moreover

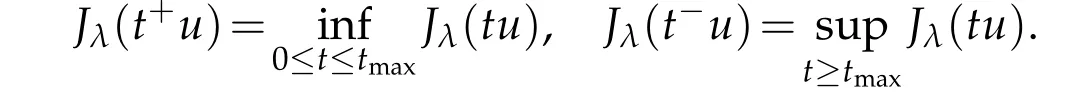
(iii)There exists a continuous bijection betweenU={u∈W{0}:||u||=1}and In particular,t−isn a continuous function forW{o0}.

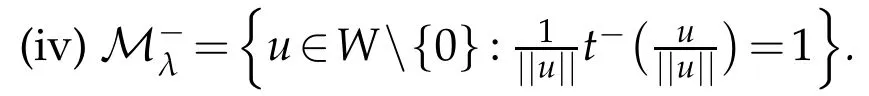
Proof.The proof is similar to that of[11]and is omitted.

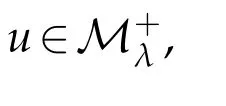
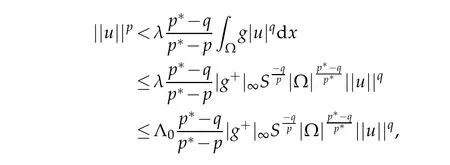
and so

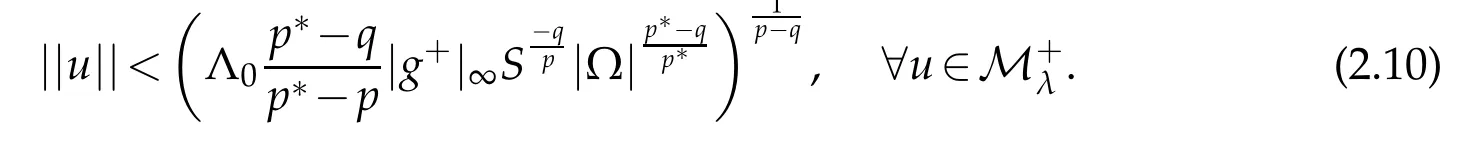
3 Proof of Theorem 1.1

Definition 3.1.(i)For c∈R,a sequence{un}is a(PS)c-sequence in W for Jλif Jλ(un)= c+on(1)and J′λ(un)=on(1)strongly in W as n→∞.

(ii)c∈R is a(PS)c-value in W for Jλif there exists a(PS)c-sequence in W for Jλ.

(iii)Jλsatisfies the(PS)c-condition in W if any(PS)c-sequence{un}in W for Jλcontains a convergent subsequence.

Now,we use the Ekeland variational principle[12]to get the following results.

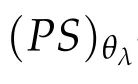
Proof.The proof of the above lemma is almost the same as that in[13].

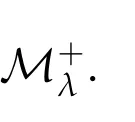
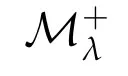
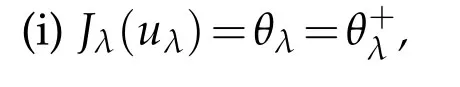
(ii)uλis a positive solution of problem(1.1),

(iii)Jλ(uλ)→0 as λ→0+.

Proof.By Lemma 3.1(i),there exists a minimizing sequence{un}for JλonMλsuch that

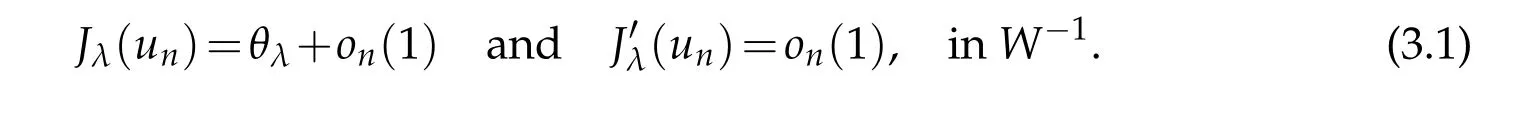
Since Jλis coercive onMλ,we get that{un}is bounded on W.Passing to a subsequence (still denoted by{un}),there exists un∈W such that

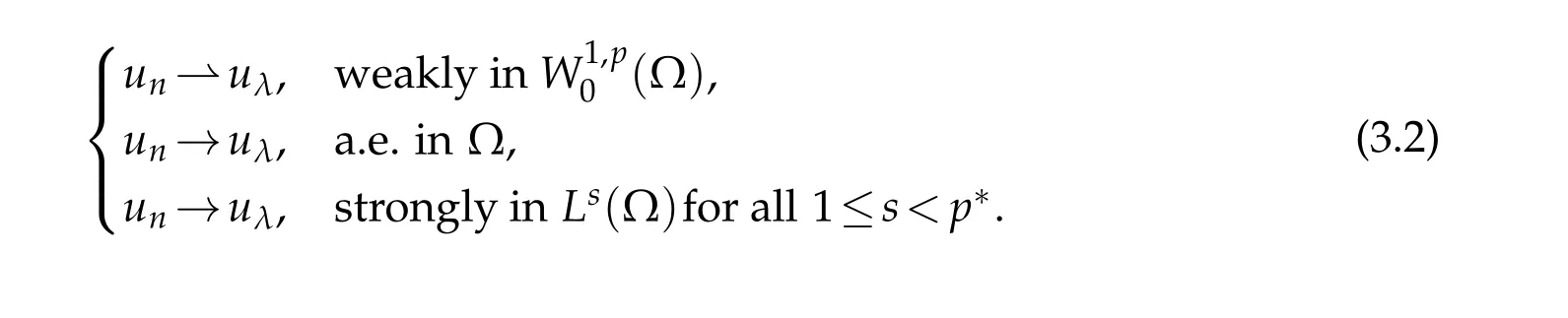
By(3.1)and(3.2),we deduce that uλis a solution of Eq.(1.1).Furthermore,the fact {un}⊂Mλimplies that

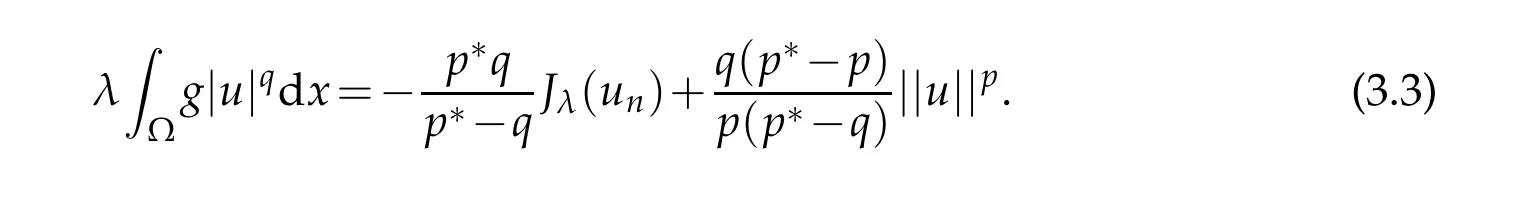
Taking n→∞in(3.3),by(3.1),(3.2)and the fact θλ＜0 we get

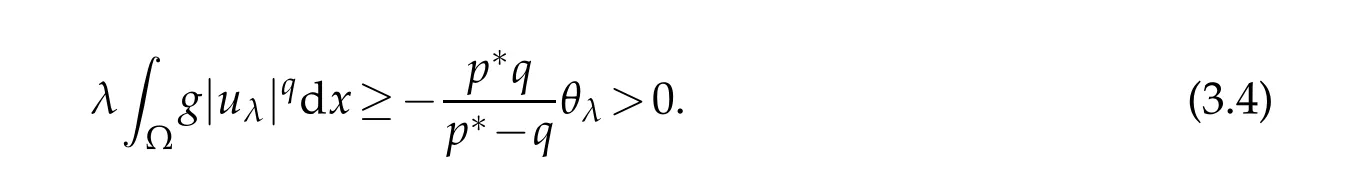
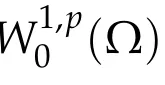
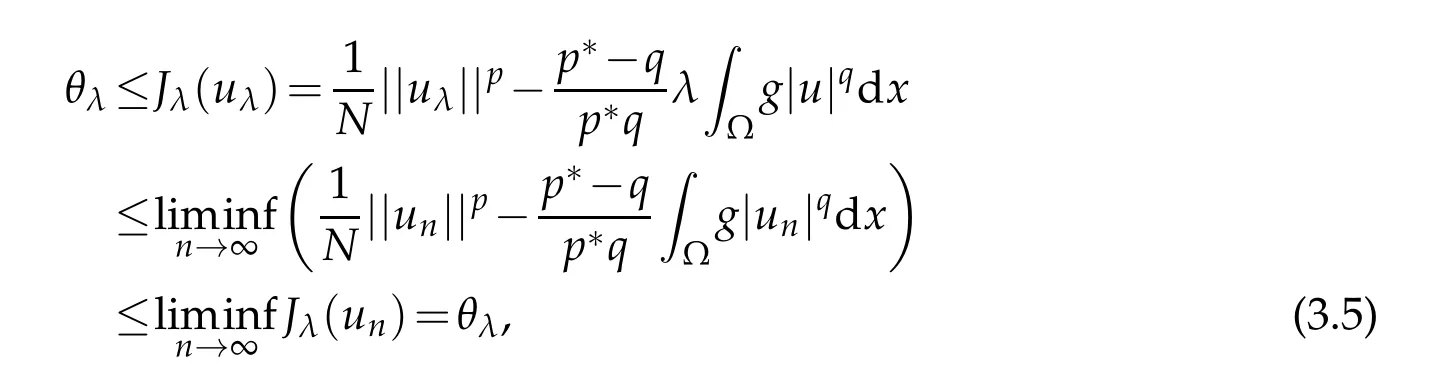
which implies that

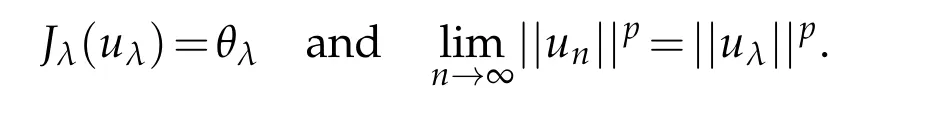
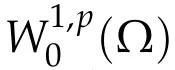
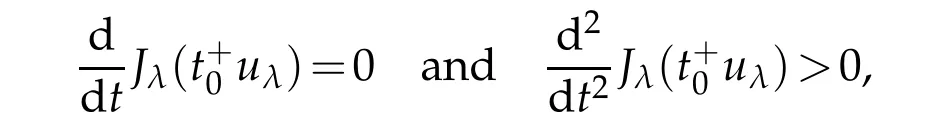
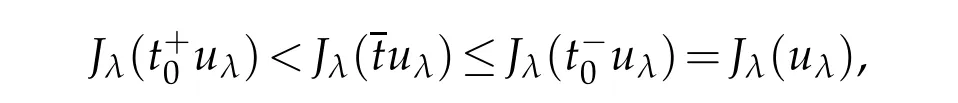
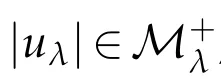
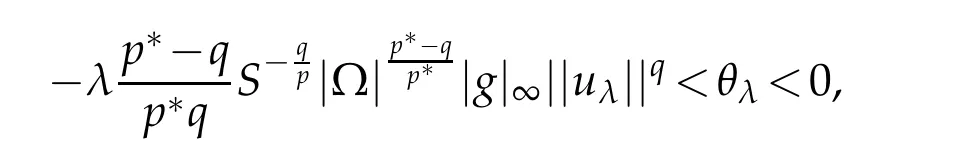
which implies that Jλ(uλ)=θλ→0 as λ→0+.

4 Proof of Theorem 1.2

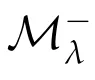
Lemma 4.1.Let{un}⊂W be a(PS)c-sequence for Jλ,then{un}is bounded in W.

Proof.The proof is similar to that of Lemma 4.1 in[15],so we omit it here.

Lemma 4.2.Assume that the conditions(F1)−(F4)and(G1)−(G2)holds.If{un}⊂W is a (PS)c−sequence for Jλwith

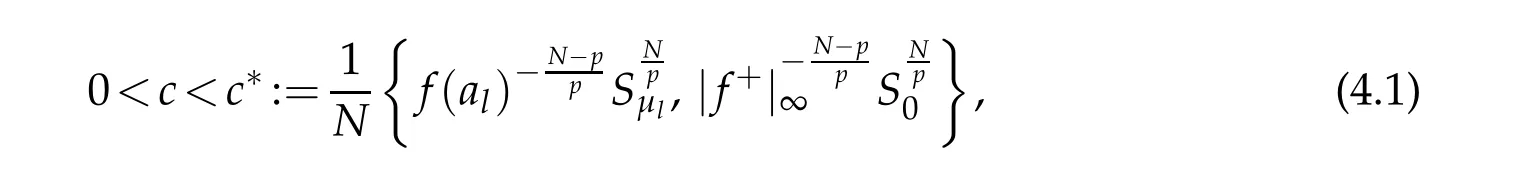
then,there exists a subsequence of{un}converging weakly to a nonzero solution of Eq.(1.1).

Proof.Let{un}⊂W be a(PS)c-sequence for Jλwith c∈(0,c∗).It follows from Lemma 4.1 that{un}is bounded in W,and then there exists a subsequence un(still denoted by un) and u∈W such that

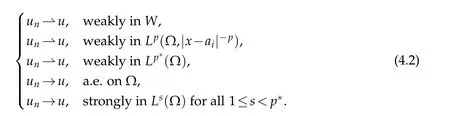
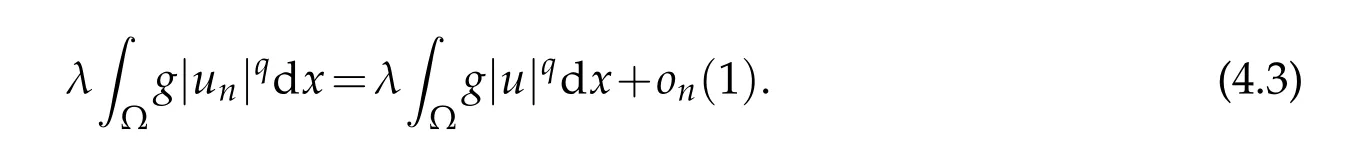
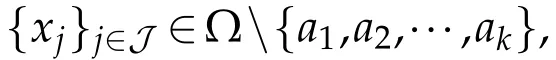
where δxis the Dirac-mass of mass 1 concentrated at the point x.By the Sobolev-Hardy inequalities,we get

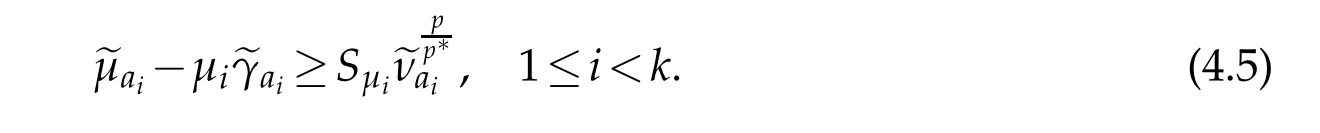
We claim thatJis finite and,for any j∈J,either

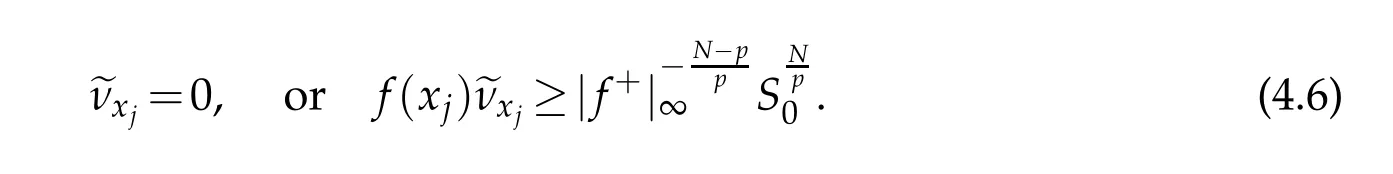
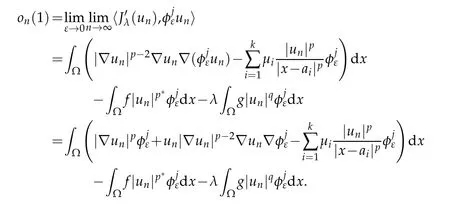
From(4.3)-(4.4),we have

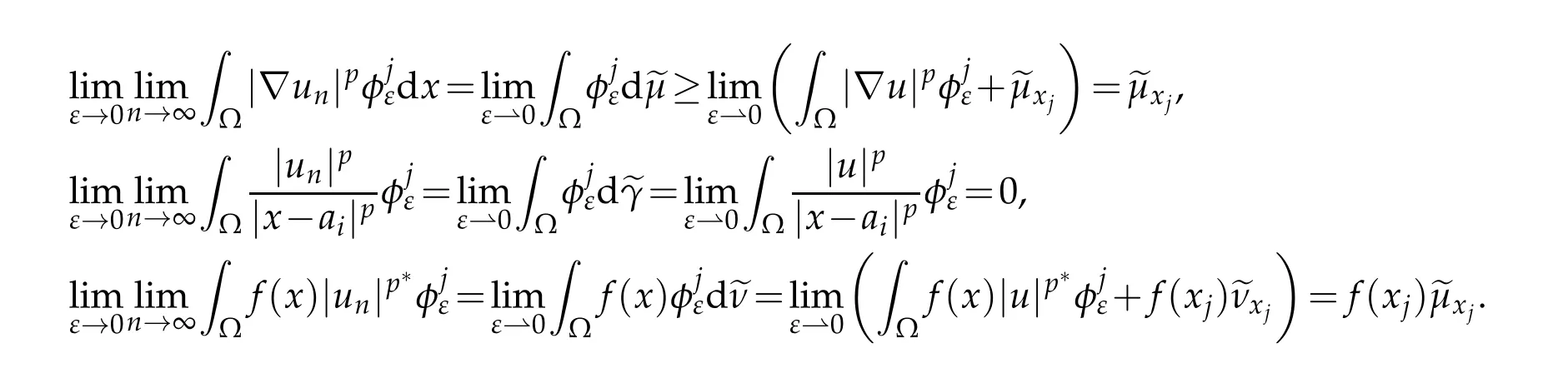
On the other hand,by H¨older inequality and boundedness of{un},it implies that

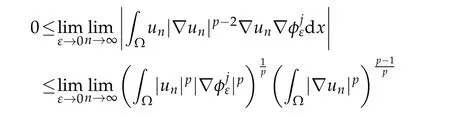
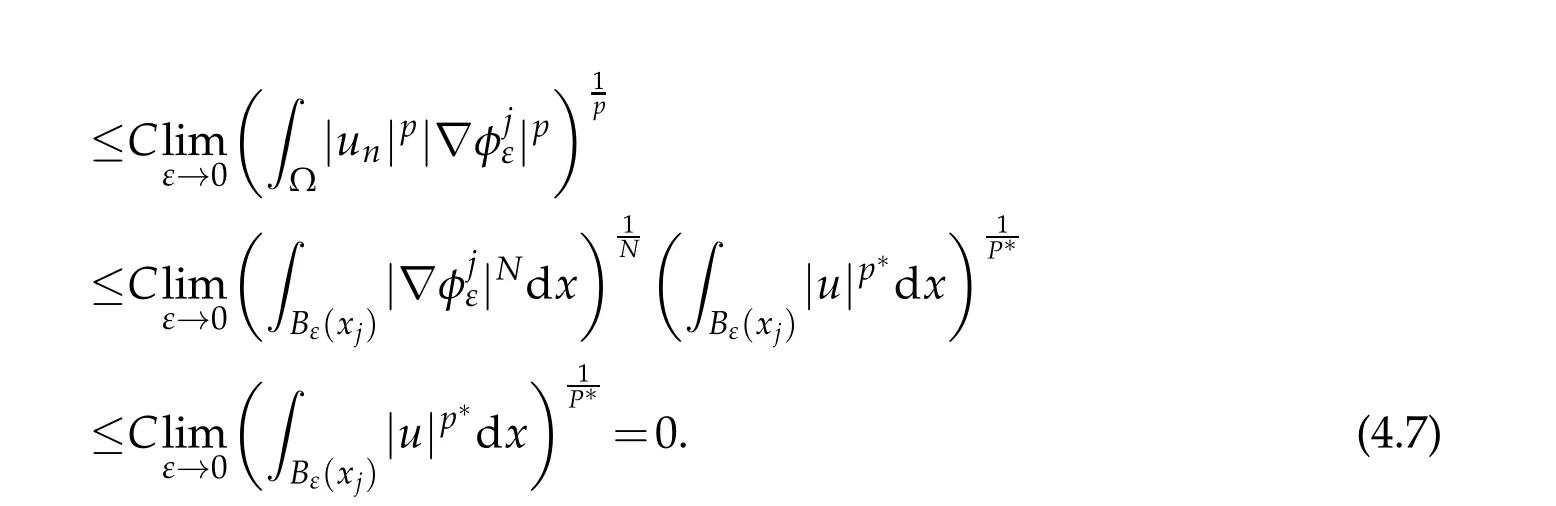
Thus,

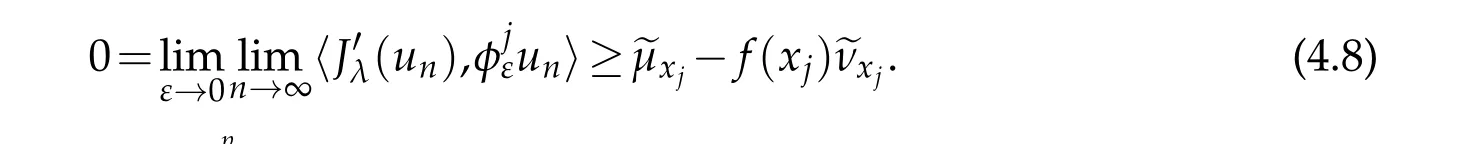
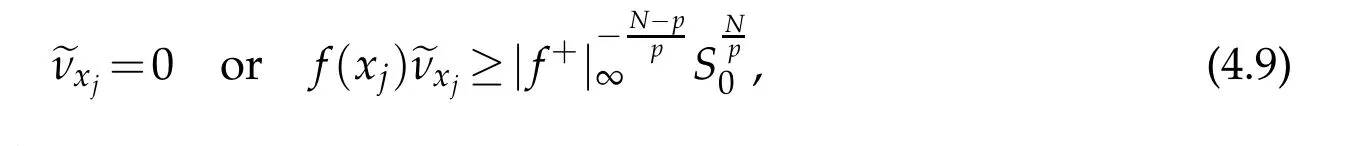
which implies thatJis finite.

Now,we study the possibility of the concentration at points ai(i=1,2,···,k).For ε＞0 be small enough such that|xj−ai|＞ε for all j∈Jand Bε(ai)∩Bε(aj)=∅for i6=j,1≤i≤k.

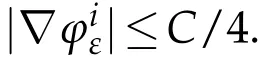
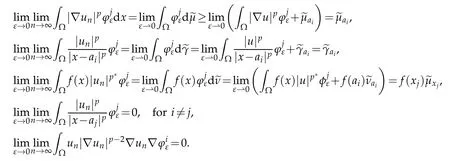
Thus,we have that

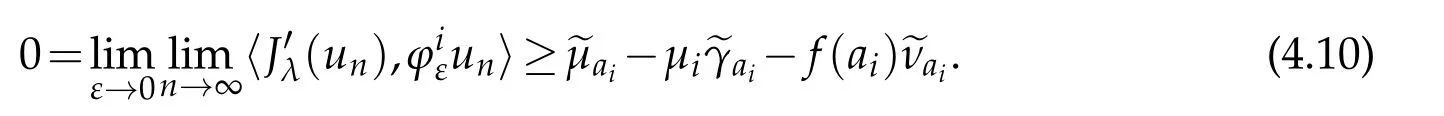
From(4.5)and(4.10)we derive that

On the other hand,from the above arguments and(4.3),we conclude that

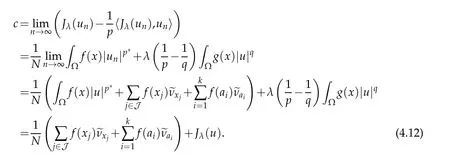
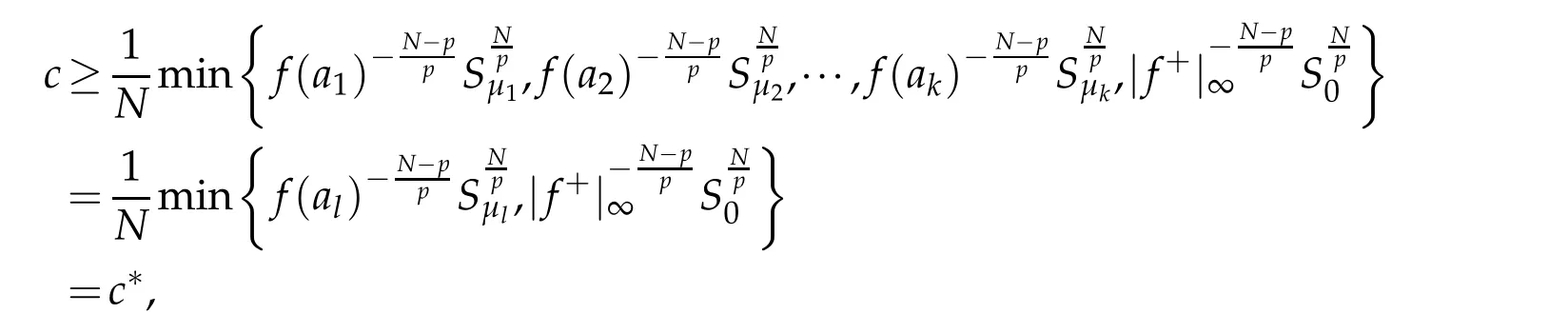
which also contradicts the assumption that c＜c∗.Therefore u0is a nonzero solution of (1.1).

Lemma 4.3.Assume that conditions(F1)−(F4)and(G1)−(G2)hold.Then for any λ＞0, there exist vλ∈W such that

Proof.To prove this lemma,we need to distinguish the following cases:

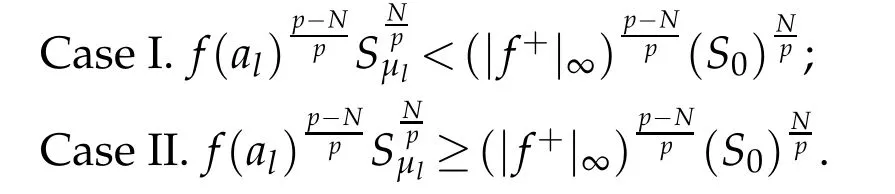
We first study Case I.The definition of c∗implies that

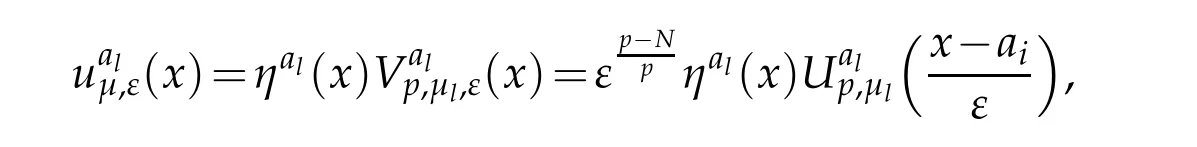
where Up,µiis a ground state solution of(1.5).Then,from[17],we have the following estimates:

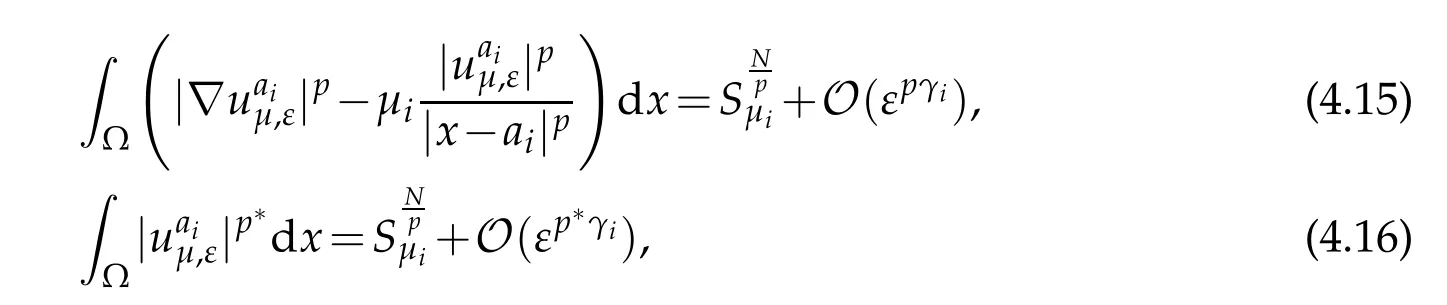
and

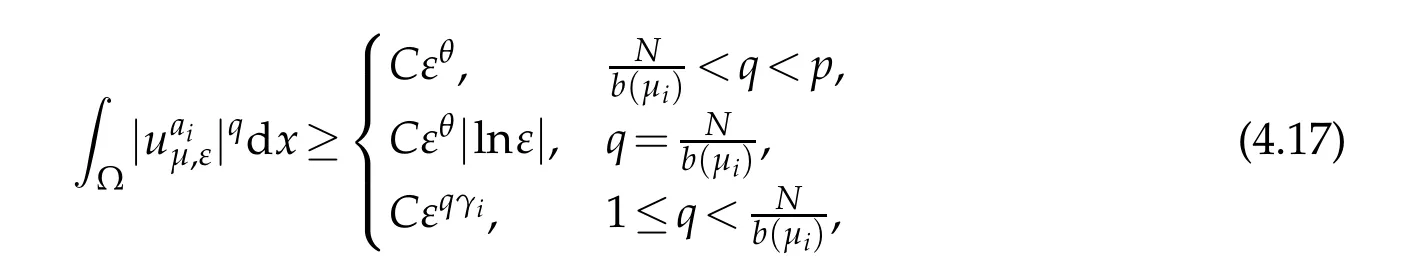
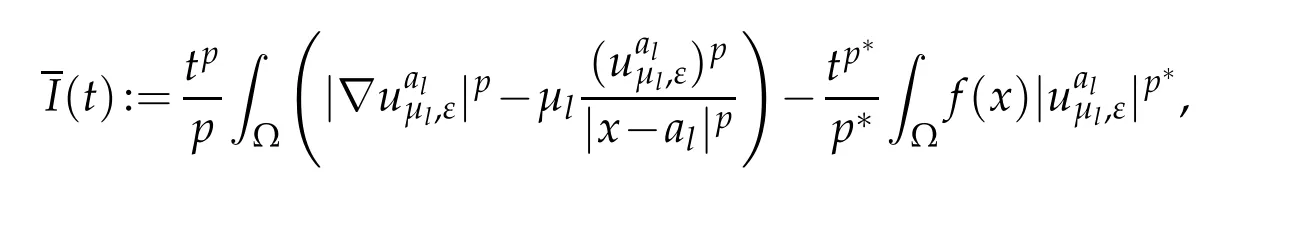
and

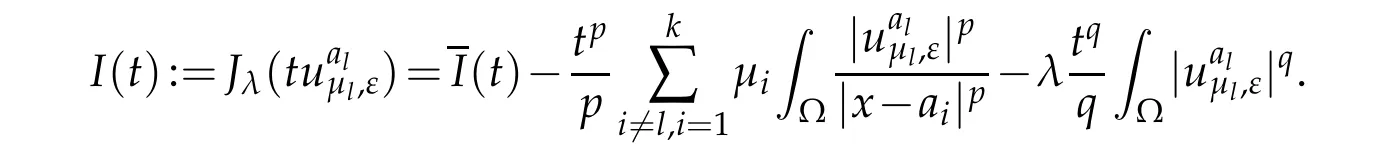
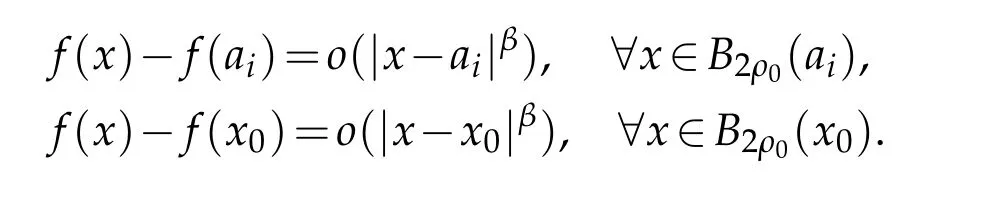
Then

which together with(40)implies that

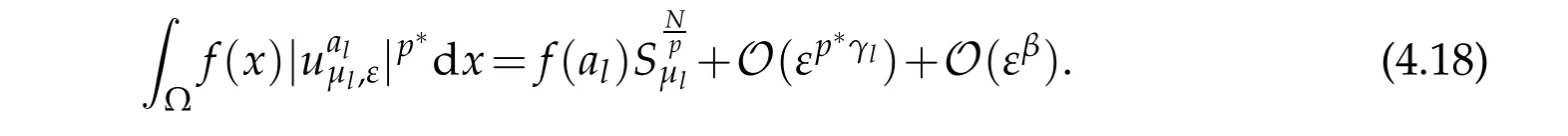
Then from the fact that

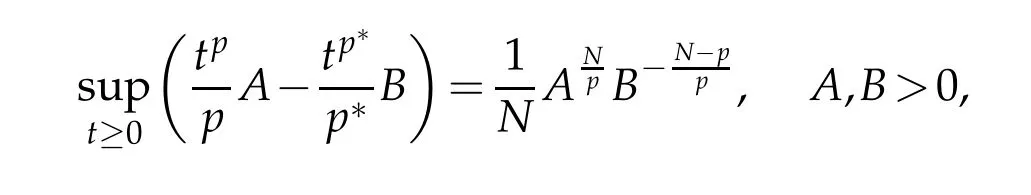
we obtain

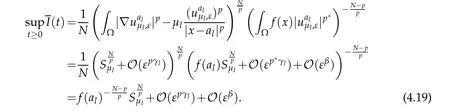
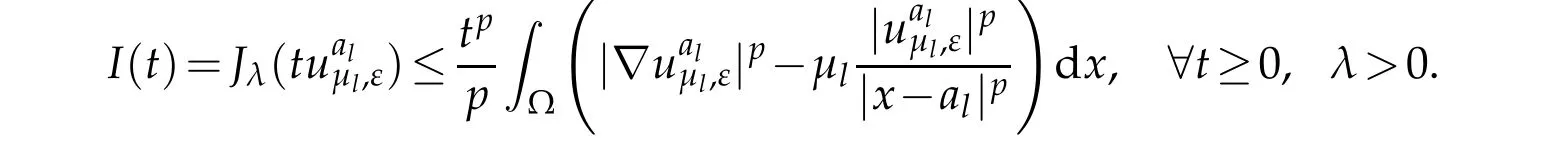
Combining this with(4.17),let ε∈(0,1),then there exists t0∈(0,1)independent of ε such that

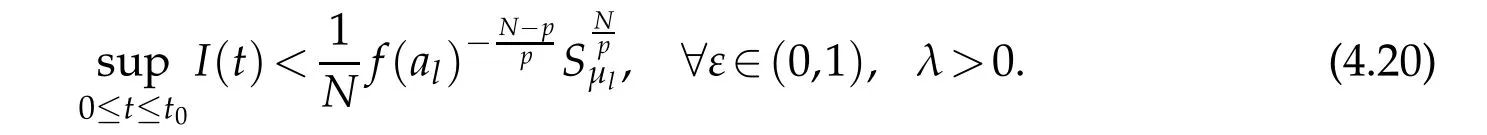
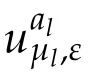
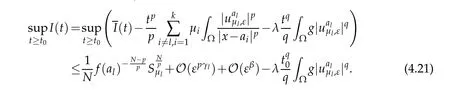
Since β＞pγl,then for λ＞0,1≤q＜p,one has that

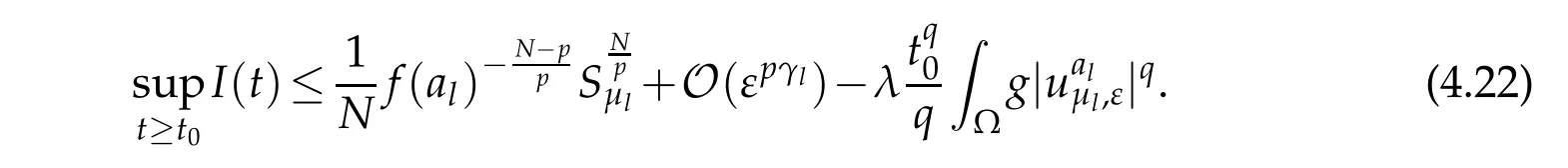
From(4.17)and(G2)it follows that

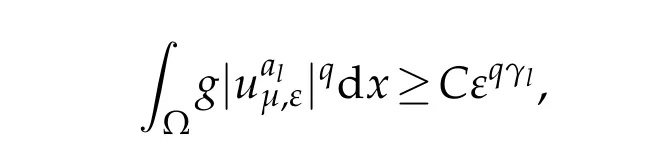
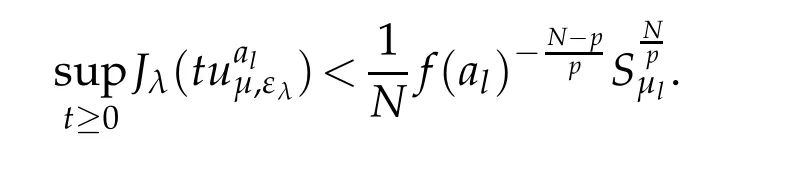
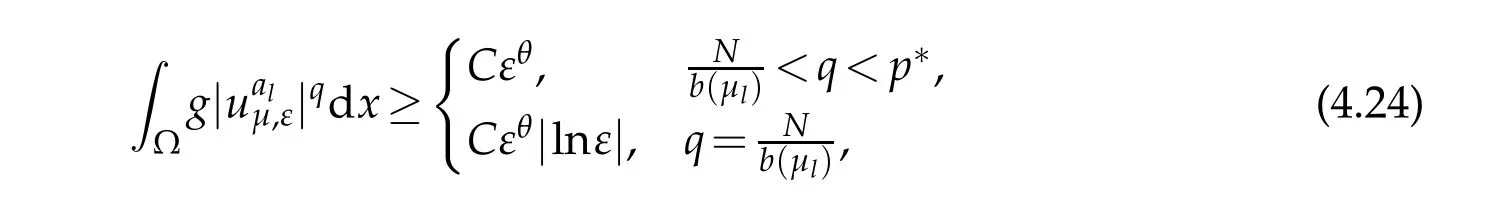
and since b(µl)q≥N then b(µl)q−qδ≥N−qδ,hence pγl＞θ.Combining this with(4.20) and(4.22),for any λ＞0,we can choose ελsmall enough such that

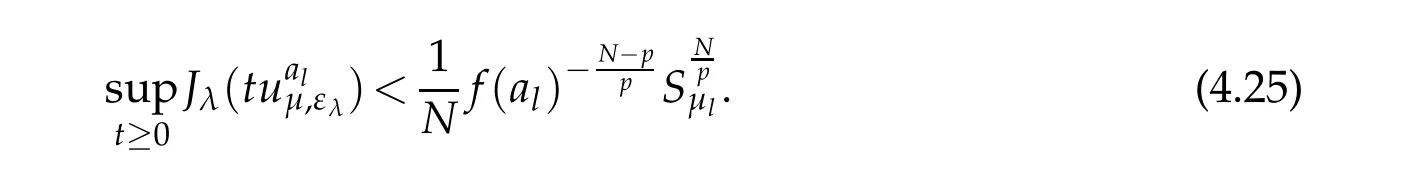
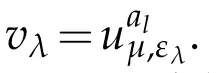
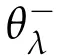
Next,we investigate case II.in this case we have

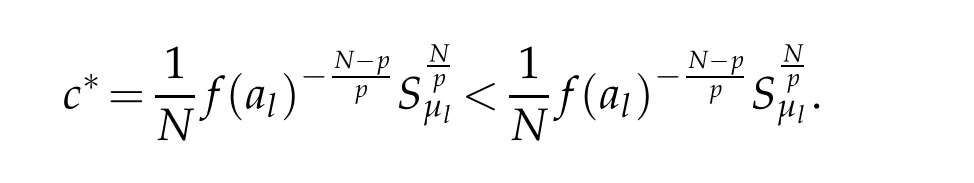
If x0=aifor some i∈{1,2,···,k},from the fact that Sµi＜S0we obtain

which is impossible.Hence x06=aifor any i∈{1,2,···,k}.

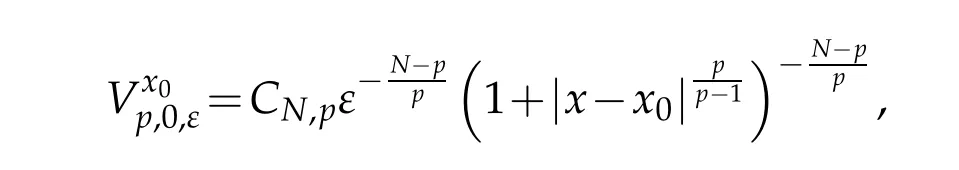
and for all x0∈Ω{a1,a2,···,ak}we define the function

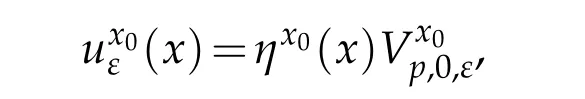
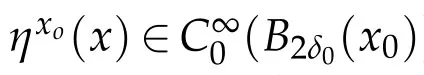
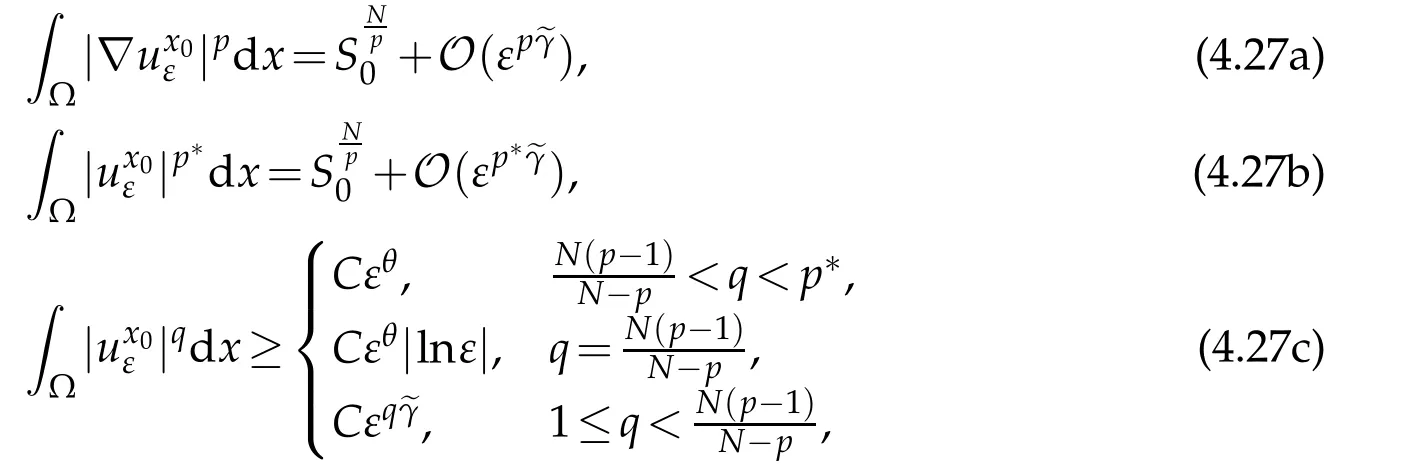
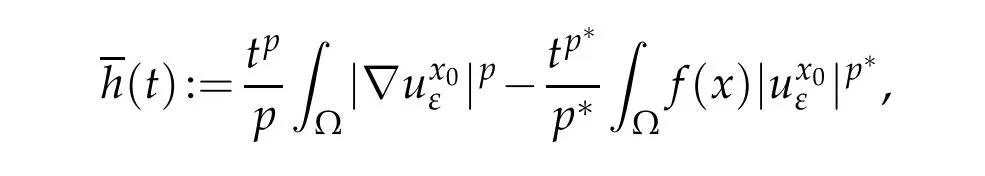
and

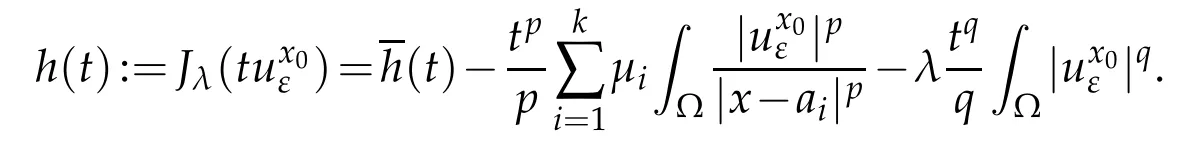
By the same argument as in Case I and(4.27a)-(4.27c),we can deduce that

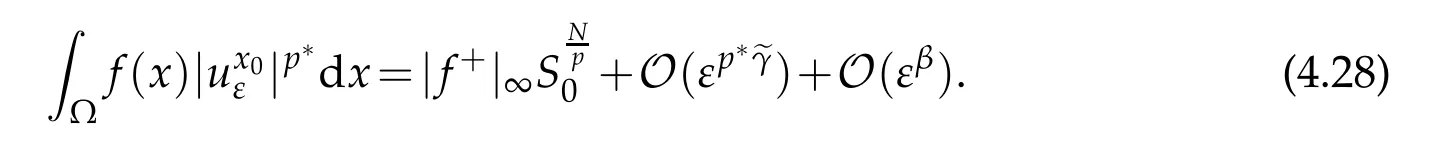
Then,we have

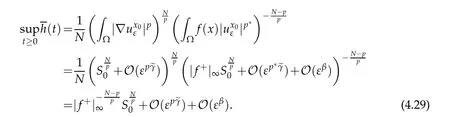
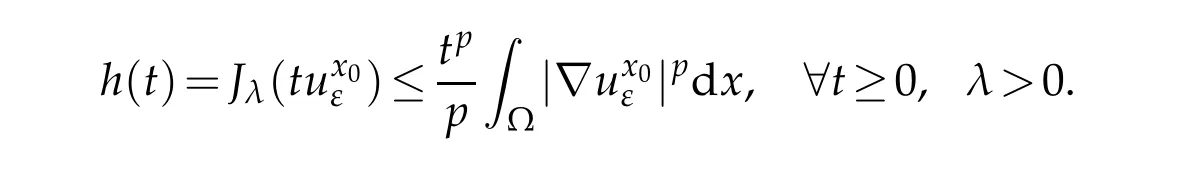
Combining this with(4.27a),let ε∈(0,1),then there exists t0∈(0,1)independent of ε such that

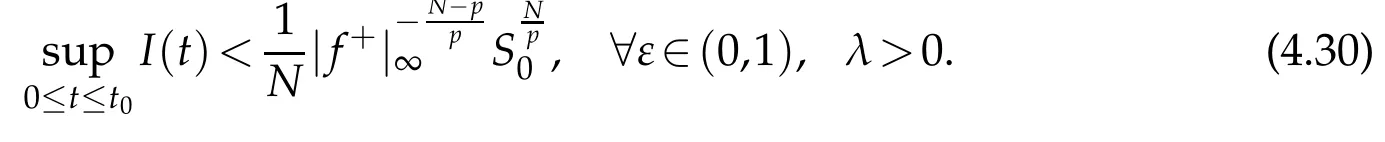
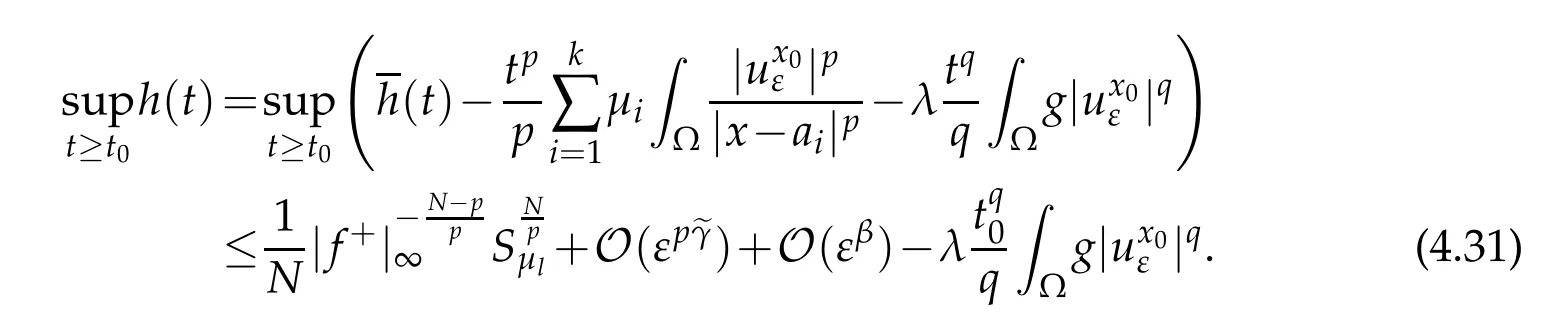
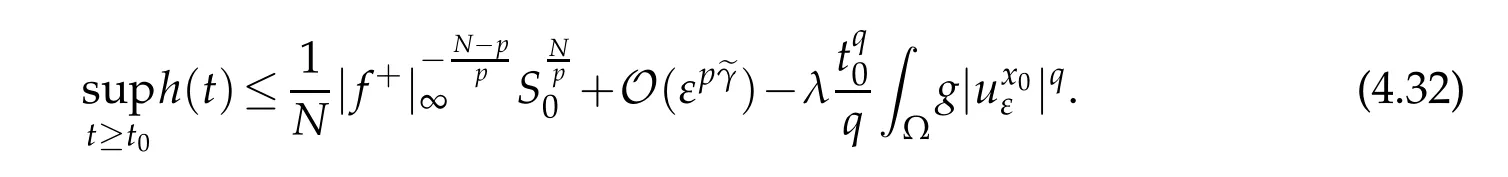
From(4.27c)and(G2)it follows that

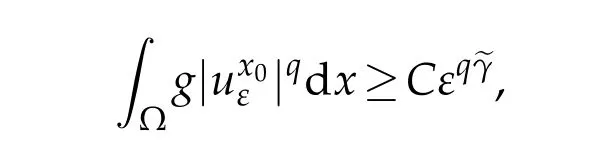
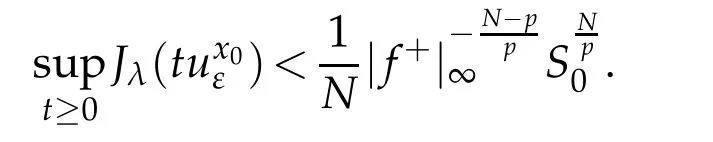
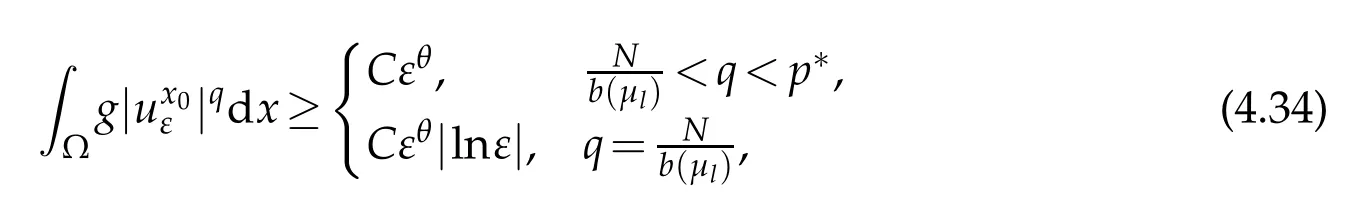
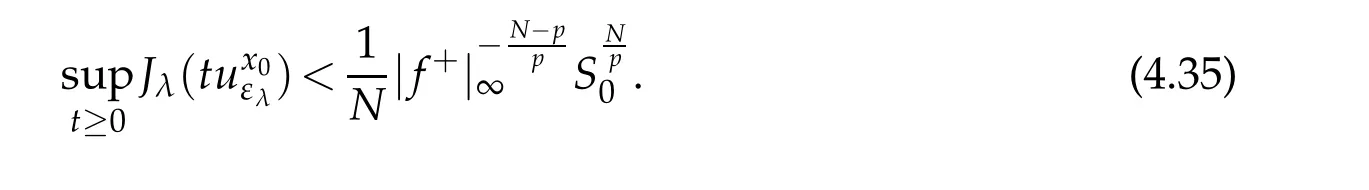
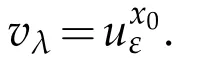
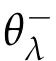
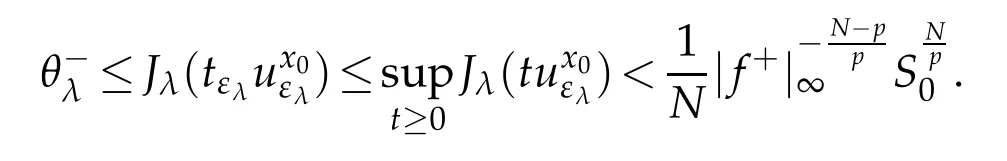
Hence Case II is proved.From Case I and II,the proof is complete.

Now,we establish the existence of a local minimum of Jλon

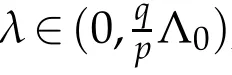
(ii)Uλis a positive solution of Eq.(1.1).

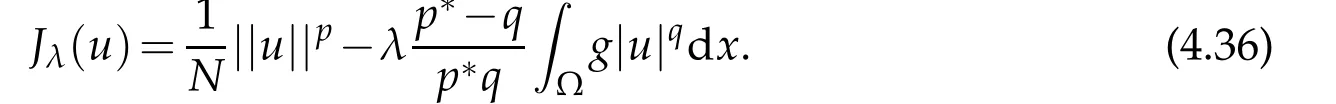
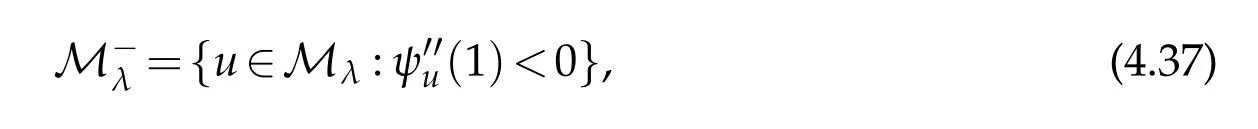
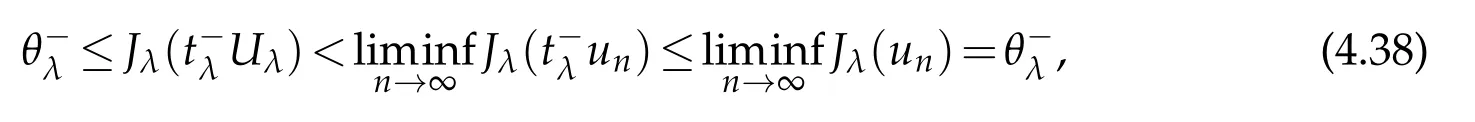
and this is a contradiction.

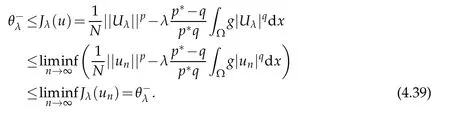
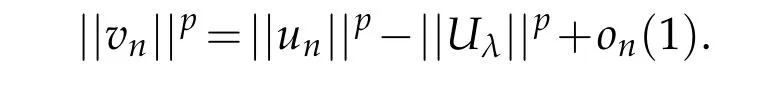
Therefore,un→Uλstrongly in W.

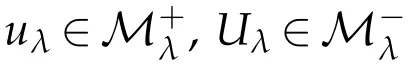
Acknowledgments

Theauthorswouldliketothank theanonymousrefereesforhis/hervaluable suggestions and comments.

[1]CaffarelliL.,Kohn R.,Nirenberg L.,First order interpolation inequality with weights.Comp. Math.,53(1984),259-275.

[2]Catrina F.,Wang Z.,On the Caffarelli-Kohn-Nirenberg inequalities:sharp constants,existence(and nonexistence),and symmetry of extremal functions.Comm.Pure Appl.Math.,54 (2001),229-258.

[3]Chou K.S.,Chu C.W.,On the best constant for a weighted Sobolev-Hardiinequality.Comm. J.Lond.Math.Soc.,48(1993),137-151.

[4]Ferrero A.,Gazzola F.,Existence of solutions for singular critical growth semilinear elliptic equations.J.Differential Equations,177(2001),494-522.

[5]Abdellaoui B.,Felli V.,Peral I.,Existence and nonexistence for quasilinear equations involving the p-Laplacian.Boll.Unione Mat.Ital.Sez.,B9(2006),445-484.

[6]Cao Y.,Kang D.,Solutions of aquasilinear elliptic problem involving a critical Sobolev exponent and multiple Hardy-type terms.J.Math.Anal.Appl.,333(2007),889-903.

[7]Cao D.,Han P.,Solutions to critical elliptic equations with multi-singular inverse square potentials.J.Differential Equations,224(2006),332-372.

[8]Felli V.,Terrcini S.,Elliptic equations with multi-singular inverse square potentials critical nonlinearity.Comm.Partial Differential Equations,31(2006),469-495.

[9]Brown K.J.,Zhang Y.,The nehari manifold for a semilinear elliptic problem with a sign changing weight function.J.Differential Equations,193(2003),481-499.

[10]Drabek P.,Pohozaev S.I.,Positive solutions for the p-Laplacian:application of the fibering method.Proc.Roy.Soc.Edinburg Sect.A,127(1997),703-726.

[11]Wu T.F.,Multiple positive solutions for a class of concave-convex elliptic problem in RNinvolving sign-changing weight.J.Funct.Anal.,258(2010),99-131.

[12]Ekeland I.,On the variational principle.J.Math.Anal.Appl.,47(1974),324-353.

[13]Wu T.F.,On semilinear elliptic equations involving concave-convex nonlinearities and signchanging weight function.J.Math.Anal.Appl.,318(2006),253-270.

[14]Vazquez J.,A strong maximum principle for some qusilinear elliptic equations.Appl.Math. Optim.,12(1984),191-202.

[15]Hsu T.S.,Multiple positive solutions for semilinear elliptic equations involving multisingular invers square potentials and concava-convex nonlinearities.Nonl.Anal.,74(2011), 3703-3715.

[16]Lions P.L.,The concentration-compactness principle in the calculus of variations.The limit case,part 1,Rev.Mat.Iberoam.,1(1985),145-201.

[17]Han P.,Quasilinear elliptic problem with critical exponents and Hardy terms.Nonl.Anal.,61(2005),735-758.

[18]Br´ezis H.,Lieb E.,A relation between pointwise convergence of functions and convergence of functionals.Proc.Amer.Math.Soc.,88(1983),486-490.

[19]Trudinger N.S.,On Harnack type inequlites and thier application to quasilinear elliptic equations.Comm.pure Appl.Math.,20(1967),721-747.

∗Corresponding author.Email address:nyamoradi@razi.ac.ir(N.Nyamoradi)

10.4208/jpde.v26.n3.1 September 2013