确定生态系统模型中高精度参数的研究
2013-04-25蒋社想
蒋社想
1 研究背景与问题描述
在要求精确制导等有关高科技的实际问题中,常常需要我们建立高精度的数学模型,这就必须高精度地确定模型中的大批参数。本文以生态系统为研究对象,利用长期积累的观测资料,高精度确定生态系统模型中的参数。
假设有一个生态系统,其中含有A和B两种生物,其中A生物是捕食者,B生物是被捕食者。假设t时刻捕食者A的数目为x(t),被捕食者B数目为y(t),根据Lotka-Volterra生态系统模型的描述[1],它们之间满足以下变化规律:
(1)
初始条件为:
(2)
其中ak(1≤k≤6)为模型的待定参数。
通过对生态系统长期观测,可以得到在tj时刻A生物数目x(tj)、B生物数目y(tj)。
根据相关的观测数据,解决以下问题[1]:
(1) 在观测数据无误差的情况下,若已知a2=1/5,根据DATA1.TXT的数据,求其它5个参数ak=(k=1,3,4,5,6)。
(2) 在观测数据无误差的情况下,根据DATA1.TXT的数据,若a2也未知,问至少需要多少组观测数据,才能确定参数ak(1≤k≤6)。
(3) 在观测资料有误差的情况下,请分别利用观测数据DATA2.TXT和DATA3.TXT,确定参数ak(1≤k≤6)的最优解。
2 观测数据分析
捕食者与被食者的模型[3]最早由Lotka和Volterra各自独立研究得出,并建立了著名的Lotka-Volterra模型。该模型解释了捕食和被捕食系统的振荡现象,即相互制约的两个种群的数目变化情况,这个模型是简单的,没有考虑到自身的阻滞作用,也没有考虑人类、环境等因素的影响作用。
本文提供的数据Data2是在15个时间单位内,以0.1个时间单位为间隔对两个种群数量的记录情况,数据容量为151。本文先根据Lotka-Volterra模型的微分方程,求出其解析解y=f(x),令其作为拟合的线型,然后利用最小二乘曲线拟合,确定模型中的参数在最小二乘意义下的最优解[2]。
数据Data3是以0.01个时间单位为间隔的观察数据,因为各种干扰因素,以及观察误差的影响,数据在微小的时间段内偏差很大,即存在高斯白噪声。本文提出先用卡尔曼滤波器将噪声滤除,再结合Data2的数据,以更高的精度来确定模型参数。
3 问题(1)分析与建模
Lotka-Volterra模型:
(3)
这是一个非线性微分方程,以下对它进行定性讨论,令
(4)
解得系统动力学方程(3)的两个平衡位置:O(0,0)及R(x*,y*),其中x*==-a3/a4,y*=-a1/a2。另外由(3)中的两个微分方程相除可以得到方程式:
(5)
对方程式(5)求解,可以得到(3)的积分方程:
根据观测数据DATA1.TXT,其部分数据如表1所示。

表1 DATA1数据
用t0时刻的观测值x(t0),y(t0)来表示积分常数k,即令F(x(t0),y(t0))=k同时根据微分方程初始条件方程(2)可得a5=10,a6=60,又已知a2=1/5,因此可以在表1给出的观测数据(i=1、2、3、4、5)中任取三组数据代入(6)式建立方程组:
(7)
利用数学和工程计算软件Maple对a1,a3,a4求解得到:
a1=-2.000003892,a3=12.00038901,
a4=-1.000044067
4 问题(2)分析与建模
问题1中,是在已知a1=1/5的前提下,我们用4个点(其中包括i=0的初始点),求解出了所有待定参数。但因为方程(7)是超越方程的缘故,使用第5个点的值无法解出合理的解。因此对于问题2本文采用曲线拟合的方法来确定模型的参数。从方程式(5)中我们可以利用Maple得出y=f(x)的解析表达式[5]:
f(x)=exp((a4*x+a3*ln(x)-a1*LambertW(a2/a1*x^(1/a1*a3)*exp(1/a1*a4*x+1/a1*(-a3*ln(2)-a3*ln(5)-10*a4+ln(60)*a1+60*a2)))-a3*ln(2)-a3*ln(5)-10*a4+ln(60)*a1+60*a2)/a1)
其中a1、a2、a3、a4为待求参数,LambertW(x)是w*exp(w)=x的解,利用f(x)作为最小二乘曲线拟合的线型,用Matlab进行拟合:
[xx,resnorm]=lsqcurvefit(@fitfun,a0,x1,y1);
fitfun:拟合函数f(x);
a0:为参数初值;
x1,y1:为DATA1中x,y向量。
由于a5,a6为t0时刻的初值,则a5=10,a6=60,通过实验发现利用六组数据进行拟合可以求出模型参数,拟合结果如表2所示。

表2 问题2数据拟合结果
5 问题(3)分析与建模
我们先用DATA2.TXT的数据如表3所示,利用类似于解决问题2方法进行拟合,得到如下的拟合结果如表4所示。

表3 DATA2部分数据

表4 DATA2数据拟合结果
由于a5,a6为t0时刻的初值,则a5=12.96229,a6=72.12302,这些值都是最小二乘意义下的最优解,然后这些参数值代入代入微分方程(3),利用Matlab仿真x=x(t),y=y(t),y=f(x)的关系曲线如图1所示。

图1 仿真结果和曲线图
DATA3中观测数据的时间间隔为0.01个时间单位,部分如表5所示。

表5 DATA3部分数据
从表中可以看出数据在微小的时间段内偏差很大,即存在高斯白噪声,我们先用Matlab将观测数据进行描点显示如图2所示。

图2 DATA3数据仿真描点
为了消除误差,本文提出先利用卡尔曼(Kalman)滤波对带有噪声的Data3数据进行滤波。卡尔曼滤波是以最小的均方误差做为估计的最佳准则,采用信号和噪声的状态空间模型,利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计,以求出当前时刻的估计值。卡尔曼滤波器包含一个线形时变系统模型和一个观测模型。
(1)系统模型

(2) 观测模型

采用预测-校正的滤波算法,其步骤如下。
(2)预测下一个误差协方差
(3)计算卡尔曼增益矩阵
(4)利用测量值更新当前估计值
(6)k=k+1返回(1)
其中(1)(2)为预测,(3)(4)(5)为校正,(6)为递推,我们设置递推的初始值为p0=H·m0;P0=I,对数据Data3进行滤波后的仿真结果如图3所示。

图3 对DATA3滤波后的仿真结果
Data2与Data3是两组不同的观测数据,都有一定程度的误差,可以先将这两组数据利用对其观测的信任程度进行加权平均,如方程式(8)所示,将可能的误差降为最小。
(8)
其中,w2,w3分别为对Data2与Data3的信任度,x(2)、y(2)为Data2的观测值,x(3)、y(3)为Data3的观测值,x(*)为经过加权平均得到的值,我们对x(*)利用最小二乘曲线拟合,进行捕食模型的参数的确定,结果如表6所示。

表6 最小二乘曲线拟合结果
由于a5,a6为t0时刻的初值,则
a5=12.837036251,a6=73.278928962。
对于Data3函数图像,以及所求模型的仿真相轨线图如图4所示。
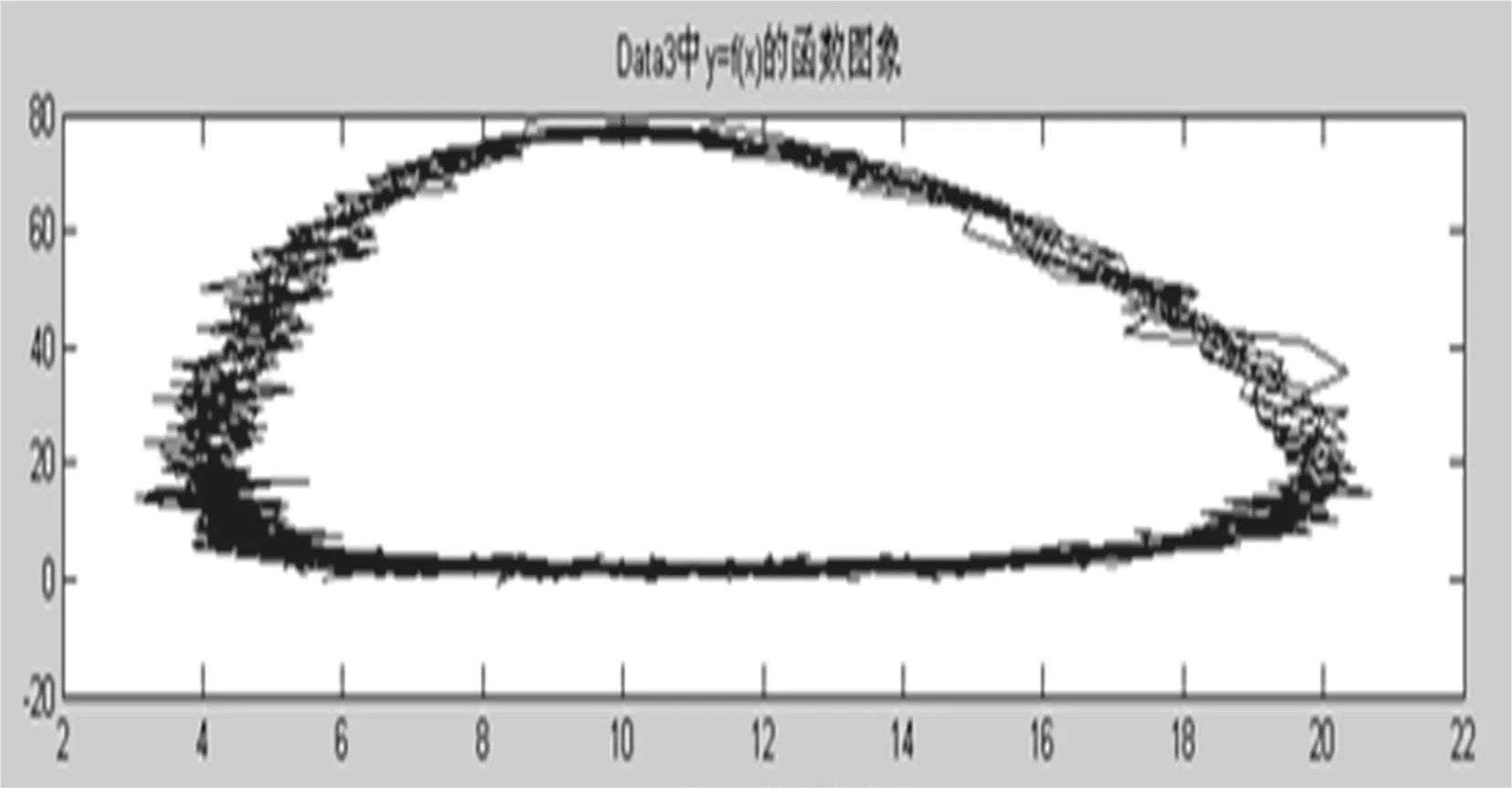
图4 DATA3相轨线图
6 模型评价
问题1是在假设观测数据无误的情况下,根据严格的公式推导得出的结果,不存在任何模型误差,只可能存在计算误差。
对于问题2、3模型本文的主要设计思想是:用求导出的模型微分方程的解做为线型,再利用最小二乘曲线拟合,来确定模型中参数ak(1≤k≤6),得到的是在最小二乘意义下的最优解。
此外,在求解问题3的过程中,为了消除误差数据,本文采用了卡尔曼滤波技术及保形插值知识。结果表明卡尔曼滤波技术在处理本题大量数据的高斯白噪声上起到了至关重要的作用,从而保证了问题参数求解的高精度。
[参 考 文 献]
[1] 第三届研究生数学建模竞赛B题[EB/OL].http//www.shumo.com.
[2] 萧树铁.数学实验[M].北京:高等教育出版社,1999.
[3] 白其峥.数学建模案例分析[M].北京:海洋出版社,2000.
[4] 赵 静,但 琦.数学建模与数学实验[M].北京:高等教育出版社,2001.
[5] 黎 捷.MAPLE 9.0符号处理及应用[M].北京:科学出版社,2004.
[6] Frank R.Giordano Maurice D.Weir William P.Fox[J].A First Course in Mathematical Modeling 3e,2003
