谷爱玲，李仲飞, 申曙光

(1. 中山大学数学与计算科学学院，广东 广州 510275；2. 广东工业大学应用数学学院，广东 广州 510006；3. 中山大学金融工程与风险管理研究中心，广东 广州 510275)

1952年文献[1]提出了均值-方差投资组合选择理论，之后此理论得到后人的不断应用及推广[2-5]。现在均值-方差准则已经成为现代投资理论的基础。自从保险公司被允许向金融市场投资以来，保险公司的最优投资问题成为学者们研究的焦点[6-10]。鉴于均值-方差准则的优点，部分学者在此准则下研究了保险公司的最优投资问题。如文献[11-14]：文献[11]依据最大值原理给出了保险公司的最优投资策略；文献[12]在粘性解的意义下给出了最优的投资策略；文献[13]根据鞅方法给出了保险公司的最优投资策略，其中保险公司的索赔过程由一维Lévy过程描述，保险公司只投资于一个无风险资产和一个风险资产，风险资产的价格过程由一般的布朗运动描述；文献[14]利用随机控制的方法得到均值-方差准则下的最优投资策略，其中保险公司的索赔过程由一维Lévy过程描述，金融市场由一个无风险资产和一个风险资产组成，风险资产的价格过程由一维的Lévy过程驱动。然而上述文献中保险公司的盈余过程只用一个变量表示，相当于保险公司只经营一种保险业务。事实上，保险公司包括多个业务部门，保险公司的盈余由各个业务部门的业绩决定。因此，采用多变量描述保险公司的风险模型显得更为合理。本文采用两个变量描述保险公司的风险模型 (可以理解为保险公司含有两个业务部门)，分别在基准准则和均值-方差准则下讨论保险公司的最优投资问题，推广了文献[14]的部分结果。

为了更好的描述保险公司的盈余过程，很多学者已经采用多变量来描述保险公司的风险模型。具体参见文献[15-19]，其中多数文献[15-18]研究了保险公司的破产概率问题，只有文献[18-19 ]涉及到了保险公司的最优投资问题。文献[18]考虑了具有两个业务部门的保险公司的最优投资问题，其中金融市场由两个几何布朗运动描述的风险资产构成，每个业务部门投资一个风险资产。在投资策略为常数的假设下，文献[18]以最小化破产概率为目标得到最优的常数投资策略；文献[19]研究了具有n个业务部门的保险公司的最优投资问题，每个业务部门投资一个风险资产，用两个不同的n维Lévy过程分别描述n个业务部门的索赔之间的相关性和n个风险资产价格跳动之间的相关性。文献[19]以最大化保险公司终端财富的负指数效用为目标，得到了最优投资策略的半解析解，且最优投资策略是与初始盈余无关的常数。文献[18]和文献[19]虽然以多变量描述保险公司的风险过程，且考虑了每个业务部门之间索赔的相关性，然而，他们得到的最优投资策略均为常数且与保险公司的索赔过程无丝毫关系，这显然与事实不符，之所以得到这样的结果与他们采用的投资准则有关。因此，为了制定更为有效合理的投资策略，必须选择合适的投资准则。于是，本文选用均值-方差作为投资准则，并且得到了与初始盈余以及保险公司的索赔相关的最优投资策略。

本文借鉴文献[19]中的保险公司的风险模型，研究了具有两个业务部门的保险公司的最优投资问题。不同于文献[19]，文中的金融市场不仅由两个风险资产组成，而且还包括一个无风险资产，这样保险公司可以将钱存入银行或向银行借款，更符合现实；而且文中的投资由专门的业务部门负责管理，这样可以在降低保险公司面临的风险的基础上，更好的利用公司的总盈余为公司带来更高利润。文中以两个相关的布朗运动分别表示两业务部门的额外保费收入，用二维的Lévy过程刻画两业务部门的索赔过程，以描述两个索赔过程在索赔次数及强度上的相关性。当Lévy测度取特殊值时，保险公司的风险模型就可转化为文献[18]中的风险模型。文中两个风险资产的价格过程是由带跳的几何布朗运动描述。由于某些风险资产(如股票)价格的跌涨与某一些经济现象， 政策条款的出台，政治事件的发生密切相关。这就引发了风险资产之间也存在一定的相关性。我们分别用两个相关的布朗运动和一个二维的Lévy过程刻画两风险资产价格的波动和跳，以描述两风险资产之间的相关性。本文分别采用基准准则和均值-方差准则建立了两个相应的优化问题。利用动态规划方法，我们得到第一个优化问题的最优投资策略和最优值函数的解析式；结合第一个优化问题的结果，利用对偶定理得到第二个优化问题的最优投资策略和有效前沿。我们发现：在只有一个业务部门且风险资产只有一个的情况下，我们的最优投资策略与文献[14]在某种情况下的投资策略一致。

1 基本假设

设(Ω,F,{Ft}0≤t≤T,P)是赋流完备的概率空间，其中Ft表示到时刻t为止所获得的信息总和，时刻t的决策基于信息流Ft，T是有限正数，代表投资期的长度。假设文中所有随机过程均为此赋流概率空间上的适应过程。假设保险公司有两个业务部门，两个业务部门的索赔风险是相关的且索赔过程由Lévy过程驱动(参见文献[19])。于是，第i个业务部门的盈余过程可描述为

Xi(t)=xi+cit+σiBi(t)-

(1)

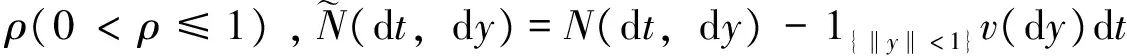
假设允许保险公司将其盈余投资于金融市场且金融市场由一个无风险资产(如债券)和两个风险资产 (如股票) 组成。无风险资产的价格过程满足

dS0(t)=r0S0(t)dt,S0(0)=s0,t∈[0,T]

(2)

其中，r0>0是常数，表示无风险利率；风险资产的价格过程由Lévy过程描述

i=1,2,t∈[0,T]

(3)

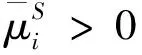
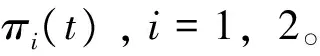
(4)

2 基准准则下的最优投资

这一节，寻求最优的投资策略使得保险公司的终端盈余尽可能达到某一个基准值(M>0)。如用距离的平方来刻画终端财富与M的偏差，则形成下列的优化问题

(5)

因此，在初始状态(t,x)下的最优值函数可以表示为

(6)

其中，Et,x[·]表示在X(t)=x下的条件期望。我们的目标是寻求优化问题(6)的最优投资策略π*以及最优值函数V(t,x)。

接下来，我们利用动态规划方法给出优化问题(6)的Hamilton-Jacobi-Bellman(简称HJB)方程。 为方便，对∀W(t,x)∈C1,2定义变分算子

π2(t)z2)1{‖z‖<1}]vS(dz)+

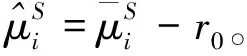
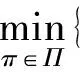
(7)

满足边界条件W(T,x)=(x-M)2。

为方便表述，记

(8)

(9)

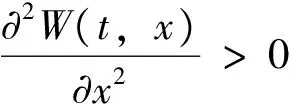
W(t,x)=P(t)x2+Q(t)x+R(t)

其中P(t)、Q(t)和R(t)是关于t的确定性连续函数，满足边界条件P(T)=1,Q(T)=-2M,R(T)=M2。根据W(t,x)的表达式，我们得到下列等式

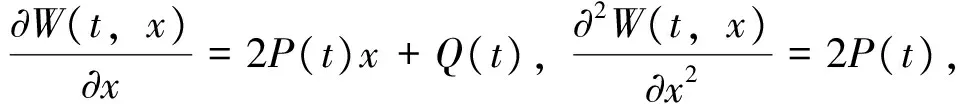
将上式代入HJB方程，简化得

(10)

对(10)式左端大括号内π1(t)和π2(t)求导，根据一阶条件得

于是，

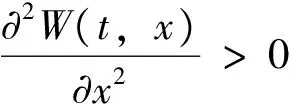
下面具体求解P(t)、Q(t)和R(t)。将π1(t,x)和π2(t,x)代入(10)式，有

Ptx2+Qtx+Rt+(2P(t)x+Q(t))(c+xr0)+

令上式中x2和x的系数以及常数项分别为零，得

Pt+P(t)(2r0-A)=0,P(T)=1;

Qt+Q(t)(r0-A)+2P(t)c=0,Q(T)=-2M;

求解上面三个一阶线性微分方程得

P(t)=e-(2r0-A)(t-T);

故

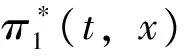
定理 2的证明与文献[20]中的定理8.1类似，从略。

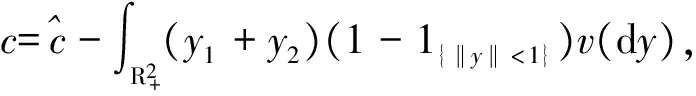
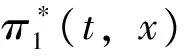
3 均值-方差准则下的最优投资

本节我们建立均值-方差模型。在定理2的基础上借助对偶理论，我们得到均值-方差问题的最优投资策略以及有效前沿，并分析了两风险资产的相关性对有效前沿的影响。

3.1 模型的建立与求解

首先，我们建立均值-方差模型。用方差来度量保险公司的风险，在终端财富期望达到某一定值M>0的情形下，选择最优的投资策略使终端财富的方差最小，即

(11)

问题(11)是一个条件极值问题，不妨令其值函数为J(x0)。我们通过拉格朗日乘子法，将问题(11)转化为无条件极值问题。 引入拉格朗日乘子λ∈R，定义拉格朗日函数

(12)

利用对偶理论，有

(13)

下面寻求最优的投资策略π*和拉格朗日乘子λ*，使得J(x0)=Jπ*(x0,λ*)。

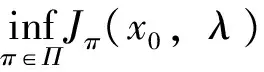
(14)

Jπ*(x0,λ)关于λ是一个凹函数，故上式对λ求导，得到最大值点λ*

(15)

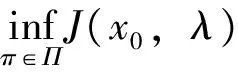
概括上述的分析过程，可得到如下定理

定理3 均值-方差问题 (11) 的有效前沿为

(16)

相应的最优投资策略为

(17)

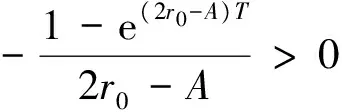
注4 定理3表明： 投资在风险资产1 (或2) 上的金额不仅与风险资产1(或2)的收益状态有关而且与资产2 (或1) 的收益情况紧密联系，这主要是资产的相关性决定的。

注5 当业务部门只有一个且金融市场只包含一个风险资产和一个无风险资产时，定理3 可退化为文献[14]中的定理4.2，其中参数α=0,λ(t)是常数。

推论1 若保险公司投资于同一个风险资产 (假设为风险资产1)，则均值-方差问题(11)的有效前沿为

相应的最优投资策略为

3.2 结果分析

不失一般性，本节以t=0时刻为例分析两支股票的相关性对均值-方差问题(11) 的最优投资策略及有效前沿的影响。

由最优投资策略的解析形式 (17) 知， 时刻t=0 时的最优投资为

可见，保险公司根据两风险资产收益率的比较而选择不同的投资形式。具体情况如下：

第二支股票的卖空金额不得超过

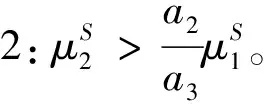
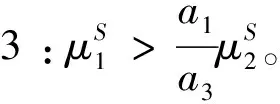
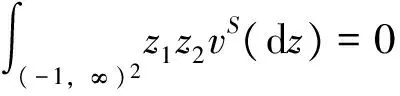
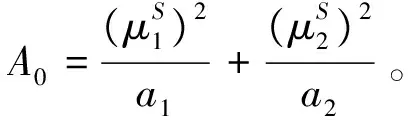
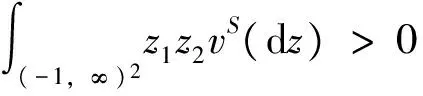
其中

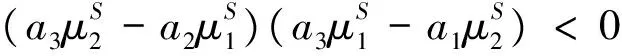
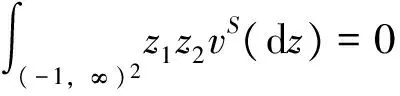
其中

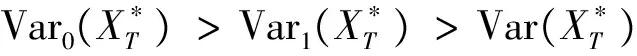
4 结束语

本文研究了具有两个业务部门的保险公司的最优投资问题，其中两业务部门的索赔之间及所投资的风险资产之间都存在一定的相关性。这一问题切合实际。如保险公司包括财产保险业务和人身保险业务，当一场车祸发生时，会同时发生财产保险的索赔及医疗费用的偿付等。本文借鉴文献[19]中的风险相关性，用两维的Lévy 测度描述两业务部门的索赔过程。金融市场由一个无风险资产和两个风险资产组成，且风险资产的价格过程是用二维的Lévy 过程表示跳的几何布朗运动描述。分别依据基准准则和均值-方差准则，我们得到了最优投资策略以及相应的最优值函数的解析形式。进一步，我们具体分析了均值-方差准则下的最优投资策略，发现投资某一资产上最优投资策略与两个风险资产的参数密切相关。同时，证实了投资于不同的风险资产比投资于同一风险资产更有利于降低风险；对于具有正相关的的两个风险资产，保险公司应该投资于价格的跳动及波动均有相关性的风险资产，这样更有利于降低保险公司在终端时刻面临的风险。

本文的不足之处是只考虑了含两个业务部门的保险公司的最优投资问题，没有考虑保险公司的再保险策略。事实上，由于粘性解的产生，同时考虑保险公司的再保险和投资问题比较难处理。但这可作为我们以后的研究方向。

参考文献：

[1] MARKOWITZ H. Portfolio selection [J]. Journal of Finance, 1952, 7: 77-91.

[2] LI D, NG W L. Optimal dynamic portfolio selection: multiperiod mean-variance formulation [J]. Mathematical Finance, 2000, 10: 387-406.

[3] ZHOU X Y, LI D. Continuous-time mean-variance portfolio selection: a stochastic LQ framework [J]. Applied Mathematics and Optimization, 2000, 42: 19-33.

[4] LIM A E B, ZHOU X Y. Mean-variance portfolio selection with random parameters in a complete market [J]. Mathematics of Operations Research, 2002, 27: 101-120.

[5] ZHOU X Y, YIN G. Markowitz mean-variance portfolio selection with regime switching: a continuous time model [J]. SIAM Journal on Control and Optimization, 2003, 42: 1466-1482.

[6] TAKSAR M, MAKUSSEN C. Optimal dynamic reinsurance policies for large insurance portfolios [J]. Finance Stochastics, 2003, 7: 97-121.

[7] PROMISLOW D S, YOUNG V R. Minimizing probability of ruin when claims flow Brownian motion with drift [J]. North American Actuarial Journal, 2005, 9: 109-128.

[8] LUO S L. Ruin minimization for insurers with borrowing constraints [J]. North American Actuarial Journal, 2008, 12: 143-174.

[9] 曾燕, 李仲飞. 线性约束下保险公司的最优投资策略 [J]. 运筹学学报, 2010, 14(2): 106-118.

[10] YANG H L, ZHANG L H. Optimal investment for insurer with jump-diffusion risk process [J]. Insurance: Mathematics and Economics, 2005, 37: 615-634.

[11] ZENG Y, LI Z F, LIU J J. Optimal strategies of benchmark and mean-variance portfolio selection problems for insurers [J]. Journal of Industrial and Management Optimization, 2010, 6: 483-496.

[12] BAI L H, ZHANG H. Dynamic mean-variance problem with constrained risk control for the insurers [J]. Mathematical Methods of Operations Research, 2008, 68: 181-205.

[13] WANG Z W, XIA J M, ZHANG L H. Optimal investment for an insurer: the martingale approach [J]. Insurance: Mathematics and Economics, 2007, 40: 322-334.

[14] DELONG K, GERRARD R. Mean-variance portfolio selection for a non-life insurance company [J]. Math Meth Oper Res, 2007, 66: 339-367.

[15] YUEN K C, GUO J Y, WU X Y. On the first time of ruin in the bivariate compound Poisson model [J]. Insurance: Mathematics and Economics, 2006, 38: 298-308.

[16] COLLAMORE J F. Importance sampling techniques for the multidimensional ruin problem for general Markov additive sequences of random vectors [J]. The Annals of Applied Probability, 2002, 12: 382-421.

[17] HULT H, LINDSKOG F. Heavy-tailed insurance portfolios: buffer capital and ruin probabilities [R]. School of ORIE, Cornell University, Technical Report No.1441, 2006.

[18] 张明善, 姚珣, 赵武,等. 二元风险模型下的保险公司最优投资策略 [J]. 管理工程学报, 2011, 25: 228-231.

[20] FLEMING W H, SONER H M. Controlled markov processes and viscosity solutions [M]. Berlin，New York: Springer, 1993.