张光俊

（金阳县双龙坝中学，四川 金阳 616253）

质数p在正整数n中的最高指数

张光俊

（金阳县双龙坝中学，四川 金阳 616253）

给出了质数p在正整数n中的最高指数p(n)的定义，讨论了p(n)的性质，并给出了在整数的整除性方面的一个应用.

质数；正整数；最高指数；整除

1 引言与p(n)的定义

在文[1]P102中有如下定理：

定理A中[x]是实数x的取整函数，即[x]是不超过x的最大整数.易知[x]有如下性质：对任一实数x及任一正整数n都有[nx]≥n[x].

另外，定理A中采用了符号p(n!)来表示素数（质数）p在n!的标准分解式中的最高指数，这样有pp(n!)|n!，但 pp(n!)+1n!.又由文[2]P88页脚“恰整除”的概念知p(n!)恰整除n!.仿此我们引入质数p在正整数n中的最高指数p(n)的定义，并研究其性质.

定义 设p是质数，n正整数，r是非负整数，如果pr|n，但pr+1n，则称r是p在n中的最高指数，简称为p在n中的指数，记为p(n).

因此，定理A中p(n!)就是质数p在n!中的指数.结合文[2]P21的定理，定理A即为

定理Aˊ质数p在n!中的指数为

由定义，对于给定的质数p，p(n)是定义在一切正整数n上的一个非负整数函数.若pn，由p0| n，则p(n)=0.若p|n，则n＞1，设n的标准分解式为

故p等于某一个且是唯一的一个pj(1≤j≤k)，由Pjαj

|n，p1,p2,…,pk是互异质数，故，从而p(n)=pj(n)=αj.因此对任一正整数n总可以设其标准分解式为

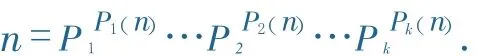
2 p(n)的性质

定理1设p是质数，n是正整数，r是非负整数，则p(n)=r的充要条件是：存在整数a使n=pra且pa.

证明：若p(n)=r，则pr|n，且pr+1n，所以存在唯一的正整数a使n=pra.如果p|a，设a=pb(b∈Z)，n=prpb=pr+1bpr+1|n，矛盾.故pa.

若存在整数a使n=pra且pa，则pr|n.如果pr+1|n，设n=pr+1b(b∈Z)，则pr+1b=prapb=ap|a，矛盾.故pr+1n，从而p(n)=r.

推论设p是质数，n是正整数，则存在唯一的正整数a使n=pp(n)a且pa.

证明：由定理1，存在整数a使n=pp(n)a且pa，显然a＞0，又由带余除法知，整数a是唯一的.

定理2设p是质数，m,n是正整数，则p(mn) =p(m)+p(n).

证明：由定理1的推论可设m=pp(m)a,pa，n=pp(n)b,pb，则mn=pp(m)+p(n)ab.如果p|ab，由p是质数得p|a或p|b，矛盾.故pab，由定理1有p(mn)=p (m)+p(n).由定理2易得下面两个推论（证明略）.

推论1设p是质数，n1,n2,…,nk∈Z+，则

推论2设p是质数，k，n∈Z+，则p(nk)=kp（n）.

定理3设p是质数，m,n是正整数，且m|n，则

证明：因m,n∈Z+，且m|n，则n∈Z+，由定理m 2有

定理4设p是质数，若n∈Z+是一个k次方数（即存在a∈Z+，使ak=n），则k|p(n)且p(n).

1

证明：因n∈Z+是一个k次方数，则nk∈Z+，由定理2的推论2有

证明：设小于等于n的质数共k个，这k个质数为p1,p2,…,pk，则n的标准分解式为

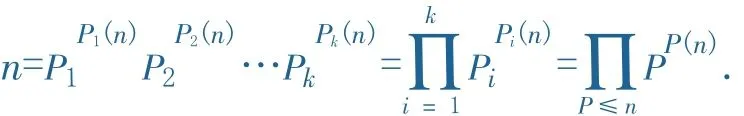
定理6设m,n∈Z+，p(m,n)是质数p在最大公因数(m,n)中的指数，p[m,n]是质数p在最小公倍数[m,n]中的指数，则

证明：（1）设m,n的标准分解式分别为

则

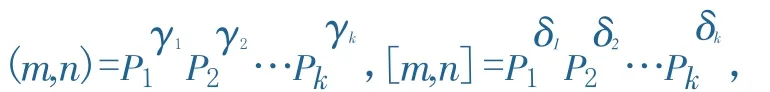
其中γi=min{pi(m),pi(n)}，δi=ma x{pi(m),pi(n)}，1≤i≤k.若p是某一pi，则

若p不同于p1,p2,…,pk，则

p(m,n)=0=p(m)=p(n)=p[m,n]，结论显然成立.

（2）若p(m)≤p(n)，则min{p(m),p(n)}=p (m)，ma x{p(m),p(n)}=p(n)，由（1）有

p(m，n)+p[m，n]=min{p(m),p(n)}+ma x{p (m),p(n)}=p(m)+p(n).

若p(m)≥p(n)，则min{p(m),p(n)}=p(n)，ma x{p(m),p(n)}=p(m)，结论仍成立.

定理7设m,n∈Z+，则m|n的充要条件是对任一质数p都有p(m)≤p(n).

证明：设m,n的标准分解式分别为则

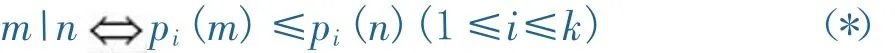
设m|n，若p是某一pi，则由（*）已有p(m)≤p (n)；若p不同于p1,p2,…,pk，则p(m)=0=p(n).

设对任一质数p都有p(m)≤p(n)，则对质数pi有pi(m)≤pi(n)(1≤i≤k)，由（*）有m|n.

定理8质数p在正整数n中的指数为

证明：因(n-1)!|n!，由定理7及定理Aˊ得

下面举一例来看定理7在整数的整除性方面的一个应用.

例 证明(n!)(n-1)!整除(n!)!.

证明：设p为任一质数，则

所以p((n!)(n-1)!)≤p((n!)!)，由定理7有(n!)(n-1)!|(n!)!.

京：高等教育出版社，1988.

[2]闵嗣鹤，严士健.初等数论（第三版）[M].北京：高等教育出版社，2003.

[1]余元希，田万海，毛宏德.初等代数研究（上册）[M].北

TheMostSignificantofPrimeNumberp in Positive Integern

Z H A N G G uang j un
(J inyang C ounty S huanglong D am M iddle S chool,J inyang S ichuan616253)

I n this paper,themost signif icant p(n)of prime number pina positi v e integer n is defined,thenaturesof p(n)arediscussed,andanappl ication isgi v en in the integer di v isibleaspects.

P rime N umber;P ositi v e I nteger;M ost S ignif icant;D i v isible

O156.1

A

1672-2094(2013)01-0151-03

责任编辑：张隆辉

2012-12-28

张光俊（1982-），男，四川隆昌人，金阳县双龙坝中学二级教师。