宋昌盛， 黎 菁， 王 莹， 李峰波， 涂颜帅， 宗丰德

(浙江师范大学非线性物理研究所，浙江金华 321004)

0 引言

1995年，Anderson研究小组［1］通过激光和蒸发冷却技术将稀薄碱金属蒸气降到极低的温度，从而在实验上首次实现了玻色-爱因斯坦凝聚态(BECs)．这为原子的波动特性提供了新的证据，也为研究和使用这种宏观量子系统提供了重要的工具．目前，对BECs的实验和理论研究多数已把目标锁定在开发、操控和揭示宏观量子现象上，如相位相干［2］、物质波衍射［3］、物质波传输［4］、物质波格栅、脉冲物质波激光［5］和量子逻辑［6］等．随着BECs实验不断取得新进展，在诸多宏观量子现象中，物质波孤子囚禁操控方面受到了特别关注．一般而言，产生吸引和排斥的BECs可通过Feshbach共振有效地加以调控［7］．其实，通过外势来囚禁操控BECs在实验上也是可行的，因为外势中的光晶格势是由波矢为2π/λ、夹角为θ相交入射的两激光束干涉叠加而成［8］．在实验中，可通过调节两激光束的夹角改变光晶格势的空间周期，也可通过改变激光束初相位随时间调制确定改变光晶格势的极小值位置．因此，在BECs的研究过程中，怎样通过调节外势来操控凝聚体已成为一个很有价值的现实问题．

本文重点研究由光晶格势和抛物势组成复合势中的BEC孤子囚禁操控动力学．笔者在此提出了一种处理上述复合势中的BEC孤子动力学的拓展变分法，将控制系统的非线性偏微分方程降阶为更为简捷的以揭示振幅、啁啾、中心位置和中心频率波动为特征的4个耦合的非线性微分方程，从而可以清楚地理解BEC孤子在复合势中的囚禁操控动力学特征，这将为BEC系统在精确量子测量和量子信息处理等方面的实验和应用提供了有力的理论参考．

1 BEC模型与变分动力学系统

在足够低的温度和平均场近似下，稀薄的玻色气体可采用带有外势的三维Gross-Pitaevskii方程［9］描述，而在一维雪茄型模型下吸引的BEC波函数被描述为带外势的非线性Schrödinger方程(NLS)［10］

式(1)中:u(x，t)是Hartree-Fock近似下的规范复数平均场变量［11］;外势场V(x，t)是光晶格势和抛物势的复合势，具体形式如下:

式(2)中:V0和V1分别是光晶格势和抛物势的强度;参数k是产生光晶格势的入射激光波数;参量x是光晶格势的最小值和抛物势最小值之间的最小偏移量．

笔者拓展已被广泛应用于哈密顿系统中的变分法，从而得到BEC的变分动力学系统．一维雪茄型BEC的控制方程(1)的拉格朗日密度［12］为

由于选用高斯函数与双曲函数作为孤子试探解的区别非常小［13］，故笔者选取带有啁啾项的试探解为

式(4)中:参量η，β，x0，ξ，φ分别代表振幅、啁啾、中心位置、中心频率和绝对相位，它们都是时间t的函数;常数A的大小由实验给定的被囚禁BEC原子总数目决定．将式(4)代入式(3)得到平均拉格朗日函变分动力学系统为:

需要指出的是，在上述推导过程中做了简化处理k/η≪1，使得exp［-k2/(2η2)］≈1，这样就拓展了文献［14］的结果，使得对BEC动力学系统稳定性分析变得简捷;另外，方程(5)～方程(8)分别反映了振幅、啁啾、中心位置和中心频率的相互作用．正是引入了啁啾项，使我们能捕捉到驱使孤子的振幅-宽度波动的二次相位变化的信息，因此，它能高质量地揭示出BEC系统的动力学特征．

2 BEC孤子的动力学演化

处理BEC变分动力学系统式(5)～式(8)的耦合非线性微分方程组的基本思路是:先求出静态解，然后再分析其稳定性［15］．这里先令

就可得静态解(η0，β0，x00，ξ0);然后，对求得的静态解进行线性稳定性分析［15］，得到特征方程为

求解特征方程(9)，得到4个特征值解

图1 5个稳定晶格势槽V(x)对应外势场与位置x之间的关系曲线

根据线性稳定性分析理论［15］可知，若4个特征值都是纯虚数，则对应的静态解是稳定的;若有一个特征值是实数，则对应的静态解将显现鞍形结构且是不4个特征值都是纯虚数，静态解是稳定的;只能产生心位置x0的变化，余弦函数将出现周期性振荡，使得特征值λ3和λ4在纯虚数(静态解是稳定的)和纯实数(静态解是不稳定的)之间转换．正是这一情形才为实现多稳定晶格势槽囚禁BECs提供了可能．要个稳定晶格势槽所对应的极小值位置(从左至右)．

表1 5个稳定晶格势槽极小值与对应位置x之间的关系

为了证实拓展变分法对于描述复合势中的BEC孤子动力学演化的充分性，笔者将对BEC变分动力学系统式(5)～式(8)的数值解与基本NLS方程的直接数值仿真进行比较，这里，笔者利用分步傅立叶变换直接数值仿真NLS方程［16］，监控基本守恒量和孤子的能量，又利用自适应步长控制的Runge-Kutta方法数值求解BEC变分动力学系统式(5)～式(8)［15，17］．

考虑一般情形，选取图1中的部分参数来讨论BEC孤子的动力学行为．图2展示了外势场稳定晶格势槽中x0=3．74的BEC孤子动力学特性．从BEC变分动力学系统式(5)～式(8)的时序图可以看出，由于啁啾的波动而导致了振幅的波动，使得BEC孤子的演化过程中出现了呼吸行为．同样，中心位置的变化会直接影响到中心频率的变化，这正好验证了前面4个耦合方程中的式(5)和式(7)．由此可知，当初始位置放置在外势场稳定晶格势槽中时，孤子的动力学演化过程保持稳定．值得指出的是，BEC变分动力学系统式(5)～式(8)的数值解与BEC控制方程(1)的直接仿真结果完全符合．

图2 初始位置放置在稳定静态解附近的BEC孤子动力学行为

3 BEC孤子的操控

接下来讨论复合势中的BEC孤子的操控．主要通过如引言所述的调制光晶格势的2种方式来实现操控BECs．第1种方式是通过复合势的“平移拖曳操控”，操控函数为

式(12)中:x1和x2分别是BEC孤子的初始位置和目标位置;t0和τ是操控参数，分别代表操控开启时间和操控持续时间．整个拖曳过程是在绝热情形下进行的，要求τ取较大的值(τ=10)．若τ很小，则整个操控过程就会完全失去对BEC孤子的引导作用，最后使得整个BEC崩塌．操控过程犹如一个机器手，在无形地平移拖曳着，使BEC孤子在操控时间范围内成功地从初始位置移动到任意目标位置．BEC孤子从初始位置的稳定晶格势槽中的x1=-6．82处操控到目标位置x2=25．00时，其对应的复合势演化如图3(a)所示．而从图3(b)中可明显看出，从初始位置到目标位置整个操控过程中复合势的强度保持不变，只是BEC孤子从初始放置的稳定晶格势槽中的x1=-26．82的A点经过平移拖曳到目标位置x2=25．00的B点，2条复合势曲线平移了一段距离而已．

图3 第1种方式操控下复合势的演化图

BEC孤子的操控动力学演化如图4所示．BEC孤子从稳定晶格势槽中的x1=-26．82处向坐标原点左边平移拖曳操控，目标位置是 x2=25．00．图 4 中的参数为 A=1．0，V0=-50，V1=0．025，k=0．1，t0=50．0，τ=10．结果表明，通过调制光晶格势中的操控函数x，实现了BEC孤子稳定平移拖曳的动力学操控．需要进一步指出的是，该操控移动过程中的变分动力学系统式(5)～式(8)的数值解与BEC控制方程(1)的直接数值模拟仿真结果非常吻合．

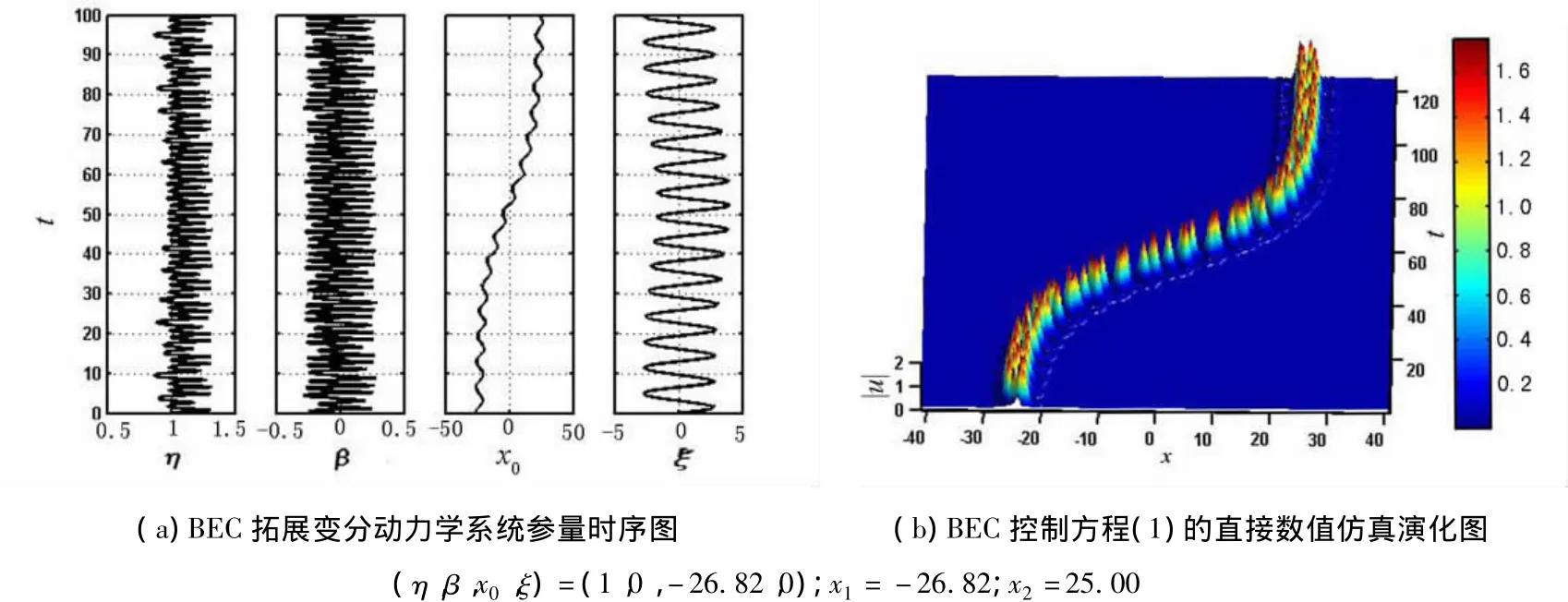
图4 第1种方式的BEC孤子的操控动力学演化图

第2种方式是通过复合势的“周期性振动操控”，操控函数为

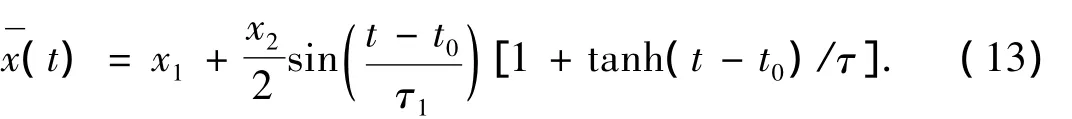
式(13)中:x1，x2，t0和τ的物理意义与第1种方式相同;τ1表示移到目标位置的操控时间．其复合势与位置和时间之间的演化如图5所示．图5中的参数为t0=15．0，τ=0．5，τ1=5．0，k=0．1，A=1．5，V0=-50，V1=0．025，x1=3．74，x2=25．00．先将 BEC孤子放置在稳定晶格势槽中x1=3．74的位置，BEC孤子被稳定地囚禁在势槽中，然后到演化时间t0=15．0时，复合势中的BEC孤子按正弦曲线轨迹开始移动，再经过5个单位时间拖曳到目标位置;随着时间的演化，BEC孤子将围绕初始位置作周期性移动，可以按需要稳定移动到周期性移动范围内的任意位置，BEC孤子的稳定操控动力学演化如图6所示．值得强调的是，该操控移动过程中的变分动力学系统式(5)～式(8)的数值解与BEC控制方程(1)的直接数值模拟仿真结果也照样非常吻合．

图5 第2种方式操控复合势V(x，t)与位置x和时间t之间的演化图

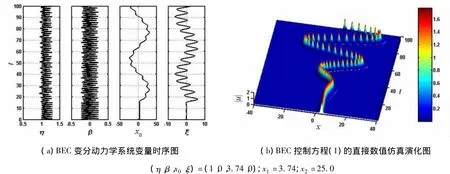
图6 第2种方式的BEC孤子的操控动力学演化图

4 结论

如何在BECs的各种外势场中管理和操控BEC孤子的问题备受研究者的关注．笔者提出了一种拓展变分法，将BEC系统经拓展变分法降阶为4个耦合非线性微分方程．该方法引入了啁啾项，使得我们能捕捉到驱使孤子的振幅-宽度波动的二次相位变化的信息，因此，它能更清晰地揭示出在光晶格势与抛物势作用下BEC孤子的动力学行为和特征．由它不仅得到了产生精确多稳定晶格势槽数目和外势场参数决定的临界比值，而且还得到了2种操控BEC孤子的基本方法．特别需要指出的是，通过调制光晶格势，成功地实现了BEC孤子从某一稳定晶格势槽为初始位置到任意目标位置的平移拖曳操控和周期性移动操控．这将为与BEC孤子操控相关的宏观量子现象的实验和应用提供了良好的理论依据．研究还表明，拓展变分法对BEC孤子系统的描述与数值仿真的结果完全符合．基于拓展变分法对于在光晶格势与抛物势作用下BEC孤子的囚禁操控动力学特性描述的有效性，可将该方法拓展到高维BEC孤子的稳定性分析和操控问题，具体工作正在进行中．

［1］Anderson M H，Matthews J R，Wieman C E．Observation of Bose-Einstein condensation in dilute atomic vapor［J］．Science，1995，269:198-201．

［2］Anderson B P，Kasevich M A．Tunnel arrays macroscopic quantum interference from atomic［J］．Science，1998，282:1686-1689．

［3］Ovchinnikov Y B，Müller J H，Doery M R，et al．Diffraction of a released Bose-Einstein condensate by a pulsed standing light wave［J］．Phys Rev Lett，1999，83:284-287．

［4］Choi D I，Niu Q．Bose-Einstein condensates in an optical lattice［J］．Phys Rev Lett，1999，82:2022-2025．

［5］Carr L D，Brand J．Pulsed atomic soliton laser［J］．Phys Rev A，2004，70:033607．

［6］Jaksch D，Bruder C，Cirac J I，et al．Cold bosonic atoms in optical lattices［J］．Phys Rev Lett，1998，81:3108-3111．

［7］Parker N G，Proukakis N P，Adams C S．Dark soliton decay due to trap anharmonicity in atomic Bose-Einstein condensates［J］．Phys Rev A，2010，81:033606．

［8］Lasinio M J，Morsch O，Cristiani M，et al．Dark soliton decay due to trap anharmonicity in atomic Bose-Einstein condensates［J］．Phys Rev Lett，2003，91:230406．

［9］Carretero-González R，Promislow K．Localized breathing oscillations of Bose-Einstein condensates in periodic traps［J］．Phys Rev A，2002，66:033610．

［10］Cataliotti F S，Burger S，Fort C，et al．Josephson junction arrays with Bose-Einstein condensates［J］．Science，2001，293:843-846．

［11］Lieb E H，Seiringer R．Proof of Bose-Einstein condensation for dilute trapped gases［J］．Phys Rev Lett，2002，88:170409．

［12］Burlak G，Malomed B A．Dynamics of matter-wave solitons in a time-modulated two-dimensional optical lattice［J］．Phys Rev A，2008，77:053606．

［13］Kutz J N，Holmes P，Evangelides S G，et al．Hamiltonian dynamics of dispersion-managed breathers［J］．J Opt Soc Am B，1998，15:87-96．

［14］Trombettoni A，Smerzi A．Discrete solitons and breathers with dilute Bose-Einstein condensates［J］．Phys Rev Lett，2001，86:2353-2356．

［15］Drazin P G．Nonlinear systems［M］．Cambridge:Cambridge University Press，1992．

［16］Mihalache D，Mazilu D，Lederer F，et al．Stable three-dimensional solitons in attractive Bose-Einstein condensates loaded in an optical lattice［J］．Phys Rev A，2005，72:021601．

［17］杨阳，宗丰德．单泡空化振动系统的动力学数值模拟［J］．浙江师范大学学报:自然科学版，2008，31(3):295-299．