王 艳, 王秀玉, 刘庆怀

(长春工业大学 基础科学学院, 长春 130012)

同伦算法由于具有大范围收敛性而成为证明非线性问题解存在的有效方法之一, 同伦算法不仅能获得解的存在性, 而且能进行求解计算, 既适用于凸优化问题, 也适用于非凸、 非线性优化问题. 文献[1-2]利用同伦方法得到了互补问题有解的条件; 文献[3-4]对多目标优化和变分不等式问题分别构造了同伦方程, 并获得了问题的解; 文献[5-7]研究了非线性优化问题的组合同伦算法; 文献[8-9]研究了光滑非凸优化的动约束组合同伦算法. 但利用组合同伦方法求解非凸、 非线性优化问题, 还需要条件： 可行域满足法锥条件, 或者满足拟法锥条件, 或者满足伪法锥条件. 当可行域不满足各类法锥条件时, 利用组合同伦方法求解非凸非线性优化问题的研究结果目前较少. 本文利用文献[9]中的动约束技术, 给出了当可行域不满足各类法锥条件时, 一类优化问题的动约束组合同伦算法.

1 预备知识

设φ:D⊂Rm→Rn是光滑映射, 对任意的y∈Rn, 记φ-1(y)={x∈Dφ(x)=y}为y在映射φ下的逆像. 如果φ在x(0)∈D处的Jacobi矩阵∂φ(x(0))/∂x行满秩, 则称x(0)是映射φ的正则点; 否则称x(0)是φ的临界点. 如果对所有的x(0)∈φ-1(y(0))都是映射φ的正则点, 则称y(0)是映射φ的正则值; 否则称y(0)是φ的临界值.

引理1(参数化的Sard定理)[10]设V⊂Rn,U⊂Rm均为开集,φ:V×U→Rp是Cr映射, 这里r>max{0,m-p}. 如果0∈Rp是φ的一个正则值, 则对几乎所有a∈V,0是φ(a,·)的一个正则值.

引理2(逆映像定理)[11]如果0是映射φ(a,·)的正则值, 则逆映射φ-1(a,·)由有限条一维光滑流形组成.

引理3(一维流形分类定理)[11]一维带边光滑流形的每个连通分支, 或者微分同胚于单位圆周, 或者微分同胚于区间(0,1]或(0,1)或[0,1].

考虑问题(P)：

记I(x)={i∈M:gi(x)=0},g(x)=(g1(x),g2(x),…,gm(x))T, ▽g(x)=(▽g1(x),▽g2(x),…,▽gm(x)),Ω={x∈Rn:gi(x)≤0,i∈M},Ω0={x∈Rn:gi(x)<0,i∈M}, ∂Ω=ΩΩ0.

假设条件如下:

(H1)f,gi(i∈M)∈Cr(r≥3);

(H2)Ω0非空且Ω有界连通;

(H3) 对任意的x∈∂Ω, {▽g(x)i∈(x)}是正独立的.

记gi(x,u)=gi(x),i∈M;Ω(μ)={x∈Rngi(x,μ)≤0,i∈M∪{m+1}};Ω0(μ)={x∈Rngi(x,μ)<0,i∈M<∪{m+1}};g(x,μ)=(g1(x),g2(x),…,gm(x),gm+1(x,μ))T. 通过选取一个适当的动约束函数gm+1(x,u), 使得如下假设成立：

无解, 其中: ∂Ω(μ)=Ω(μ)Ω0(μ);I(x,μ)={i∈M∪{m+1}gi(x,μ)=0};

(H5)gm+1(x,μ)关于x及μ充分光滑, ∀μ∈[0,1]θ,Ω0(μ)非空,Ω(μ)有界且Ω(0)=Ω, ∀x∈∂Ω(μ), {▽xgi(x,μ)i∈I(x,μ)}正独立;

2 主要结果

(1)

其中:y=(y1,y2,…,ym,ym+1)T;g(x,μ)=(g1(x,μ),g2(x,μ),…,gm+1(x,μ))T;

(2)

问题(P)的K-K-T方程为

(3)

方程(2) 的解必为方程(3)的解, 且显然有H(ω(0),ω(0),1)=0.

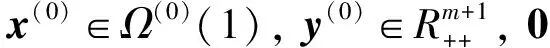
证明:H(ω,ω(0),μ)的Jocobi矩阵记为H′(ω,ω(0),μ),

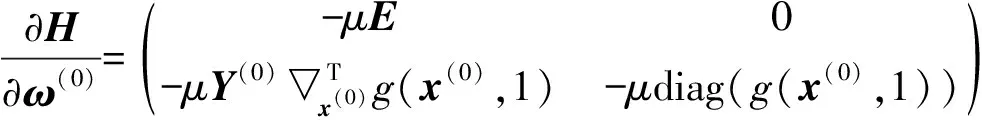
从而H′(ω,ω(0),μ)行满秩, 由引理1知,0是H(ω,ω(0),μ)的正则值. 又由引理2知,H-1(0)所含曲线是光滑的, 且H(ω(0),ω(0),1)=0, 因而, 存在一条起始于(ω(0),1)的光滑曲线, 记为Γω(0).

证明: 用反证法. 假设光滑曲线Γω(0)无界, 则必存在点列(x(k),y(k),μk)∈Γω(0), 使得‖(x(k),y(k),μk)‖→∞(k→∞). 由同伦方程(1)的第二式得

(4)

(5)

将式(5)整理如下：

情形1)μ*=1. 式(6)两边取极限得

与(H6)矛盾.

式(7)两边取极限得

(8)

证明:Γω(0)的存在性及有界性由引理4和引理5可知. 又由引理3知,Γω(0)或微分同胚于单位圆周, 或微分同胚于单位区间(0,1]. 因为

其中:

3)μ*=0, (x(*),y(*))∈Ω×R+, ‖y(*)‖<∞.

3 路径跟踪算法及算例

算法1Euler-Newton法[12].

输入ω(0), 选取初始步长h0>0, 正数J1=2,J2=5及小正数ε1,ε2,α,β∈(0,1), 并且令μ0=1,k=0.

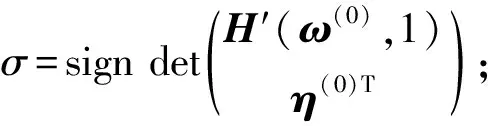
2) 计算预估点(ω(k+1,0),μk+1,0)=(ω(k),μk)+αlhkη(k), 其中l是使得(ω(k+1,0)μk+1,0)∈Ω0×(0,1]成立的最小正整数.

3) 计算校正点(ω(k+1),μk+1): 若使(ω(k+1,0),μk+1,0)∈Ω0×(0,1]成立的最小正整数j≤J2, 且‖H(ω(k+1, j),μk+1, j)‖>ε1, 则

(ω(k+1, j),μk+1, j)=(ω(k, j-1),μk, j-1)-βl(H′(ω(k, j-1),μk, j-1))+H(ω(k, j-1),μk, j-1),

其中l是使得(ω(k+1, j),μk+1, j)∈Ω0×(0,1]成立的最小正整数,j∶=j+1.

若‖H(ω(k+1, j),μk+1, j)‖≤ε1, 且j≤J1, 则令(ω(k+1),μk+1)=(ω(k+1, j),μk+1, j),hk+1=min{h0,1.25hk}, 转4);

若‖H(ω(k+1, j),μk+1, j)‖>ε1,hk+1=0.75hk,k∶=k+1, 则转3).

4)μk+1≤ε2, 则停; 否则置k=k+1, 转1).

在算法的步骤3)中, (H′(ω,μ))+=H′(ω,μ)T(H′(ω,μ)H′(ω,μ)T)-1是H′(ω,μ)的Moore-Penrose逆.

例1

可行域不满足伪锥条件, 构造动约束函数如下：

[1] YU Qian, HUANG Chong-chao, WANG Xian-jia. A Combined Homotopy Interior Point Method for the Linear Complementarity Problem [J]. Applied Mathematics and Computation, 2006, 179(2): 696-701.

[2] DING Jun-di, YIN Hong-you. A New Homotopy Method for Nonlinear Complementarity Problems [J]. Numericla Mathematics: A Journal of Chinese Universities (English Series), 2007, 16(2): 155-163.

[3] Song W, Yao G M. Homotopy Method for a General Multiobjective Programming Problem [J]. J Optim Theory Apply, 2008, 138(1): 139-153.

[4] XU Qing, YU Bo, FENG Guo-chen. Homotopy Method for Solving Variational Inequalities in Unbounded Sets [J]. Journal of Global Optimization, 2005, 31(1): 121-131.

[5] LIN Zheng-hua, YU Bo, FENG Guo-chen. A Combined Homotopy Interior Point Method for Convex Nonlinear Programming [J]. Appl Math Comput, 1997, 84(2/3): 193-211.

[6] LIU Qing-huai, YU Bo, FENG Guo-chen. The Homotopy Interior-Point Method for Nonconvex Nonlinear Programming Problem Based on Quasi-normal Cone Condition [J]. Acta Mathematicae Applicatae Sinica, 2003, 26(2): 372-377. (刘庆怀, 于波, 冯果忱. 基于拟法锥条件的非凸非线性规划问题的同伦内点法 [J]. 应用数学学报, 2003, 26(2): 372-377.)

[7] LIN Zheng-hua, LI Yong, YU Bo. A Combined Homotopy Interior Point Method for General Nonlinear Programming Problems [J]. Appl Math Comput, 1996, 80(2/3): 209-226.

[8] SHANG Yu-feng, YU Bo. Boundary Moving Combined Homotopy Method for Nonconvex Nonlinear Programming and Its Convergence [J]. Journal of Jilin University: Science Edition, 2006, 44(3): 357-361. (商玉凤, 于波. 凸规划的动边界组合同伦方法及其收敛性 [J]. 吉林大学学报: 理学版, 2006, 44(3): 357-361.)

[9] SHANG Yu-feng. Constraint Shifting Combined Homotopy Method for Solving Nonlinear Programming, Equilibrium Programming and Variational Inequality [D]: [Ph D Thesis]. Changchun: Jilin University, 2006. (商玉凤. 解非线性规划、 均衡规划和变分不等式问题的动约束组合同伦方法 [D]: [博士学位论文]. 长春: 吉林大学, 2006.)

[10] Allgor E L, Georg K. Numerical Continuation Method: An Introduction [M]. Berlin: Springer-Verlag, 1990.

[11] Naber G L. Topological Method in Euclidean Space [M]. London: Cambridge University Press, 1980.

[12] FAN Xiao-na, YU Bo. A Smoothing Homotopy Method for Solving Variational Inequalities [J]. Nonlinear Analysis: Theory, Method & Applications, 2009, 70(1): 211-219.