杨凯凡

（陕西理工学院，汉中 723000）

不可约非负矩阵的特征值问题

杨凯凡

（陕西理工学院，汉中 723000）

从正矩阵特征值的Perron定理出发,根据正矩阵与不可约非负矩阵的关系,对Perron定理作进一步推广,得出不可约非负矩阵特征值的一些结论。

正矩阵；不可约非负矩阵；特征值

不可约非负矩阵在数理经济学、概率论、组合论等多个领域的理论研究中都有着非常重要的作用，特别是不可约非负矩阵的特征值问题的研究。本文首先给出正矩阵特征值的Perron定理,然后将该定理推广到不可约非负矩阵上,给出关于不可约非负矩阵特征值的一些相关结论。

1 相关概念

定义 1［1］设 A=(aij)∈Rm×n, 如果 aij≥0,i=1，2，3，…,m；j=1，…，n,即A的元素是非负的,则称 A为非负矩阵, 记作 A≥0； 若 aij＞0 （i=1，2，3， …，m；j=1，2，3，…,n），则称 A 为正矩阵 ,记为 A＞0。

定义2[1]设A∈Rn×n(n≥2),若存在n阶置换矩阵P,使得则称A为可约矩阵,否则称A为不可约矩阵。其中A11为r阶方阵,A12为n－r阶方阵(1≤r≤n)。

2 Perron定理

引理1 设A∈Rn×n,并且A≥0,x∈Rn是一个不为零的非负向量,并且设 ξ∈R 满足 Ax=xξ,则 ρ(A)＞ξ。

证明 不妨设 ξ≥0，取 ζ＞0,满足 Ax=x(ξ+ζ)x。令B=A/(ξ+ζ),则易得 Bkx≥Bk－1x≥BBk－2x≥…≥x，对一切自然数k成立。因x≥0且x≠0,则k→∞时,Bk不趋于 0，ρ(B)≥1,即 ρ(A)≥(ξ+ζ)＞ξ。

引理 2 设矩阵 A∈Rn×n，且 A＞0，z=(z1,L,zn)T∈Cn,z≠0,满足 Az=λz,|λ|=ρ(A),则有 λ=ρ(A)＞0,z＞0 和 A|z|=ρ(A)|z|成立。由以上引理易证下面的定理成立。

定理 3 设 n阶矩阵 A=aij＞0,且 ρ(A)为其谱半径，则有结论：

（1）ρ(A)为 A 的正特征值,其对应的一个特征向量为正向量；

（2）A 的任何其他特征值，都有|λ|＜ρ(A)；

（3）ρ(A)是 A 的单特征值。

此定理给出了正矩阵特征值的有关结论,而正矩阵是不可约非负矩阵的一种特殊情况。为此,经过改进可将此结论推广到不可约非负矩阵上去，即有定理4。

定理4 设A∈Rn×n是不可约非负矩阵，则有以下结论：

（Ⅰ）有一个正的实特征值等于其谱半径ρ(A)；

（Ⅱ）ρ(A)的特征向量可取正的；

（Ⅲ）ρ(A)是 A 的单特征值；

（Ⅳ）不存在相应A的其他特征值的非负特征向量。

证明 先证结论（Ⅰ）和（Ⅱ），根据谱半径的定义,A存在特征值λ和相应的特征向量x∈Cn，满足Ax=λx，|λ|=ρ(A),因此,利用 A 的非负性,有 ρ(A)|x|=|λ||x|≤A|x|。

由此递推,得

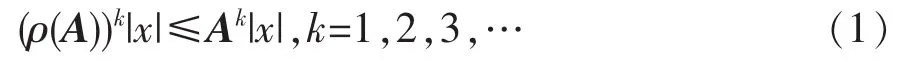
于是

于是(I+A)n－1＞0,(I+AT)n－1＞0。将 Perron 定理应用于(I+AT)n－1＞0,得知其有特征值 ρ((I+A)n－1)及存在相应的特征向量y＞0；从而利用转置可得

用yT左乘式（1），然后应用式（3）并且约去因子yT|x|＞0，有

另一方面,(I+A)n－1＞0 的特征值是(1+μ)n－1,μ∈λ(A)。故存在μ^=λ(A),使得 ρ((I+A)n－1)=(1+μ^)n－1，将其代入式（3），可得 1+ρ(A)≤|1+μ^|≤1+|μ^|≤1+ρ(A)。

由此推出μ^=|μ^|=ρ(A)，因而式（4）等号成立,并因此式（2）等号成立,即

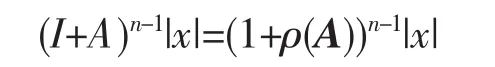
根据这一等式,连同(I+A)n－1＞0 及|x|≠0,推出|x|＞0;再再据式（1），有 A|x|=ρ(A)|x|。 这表明：ρ(A)＞0 是 A 的特征值,|x|＞0是相应的特征向量。

由以上证明可知,属于ρ(A)的任一特征向量μ必有|μ|＞0，因此,可证 ρ(A)的几何重数为 1。 另外,对A和AT应用结论（Ⅱ），属于ρ(A)的左、右特征向量μ,ν可取作正的,因而 νTμ＞0。 因此， ρ(A)是 A 的单特征值。

反证法。假定存在非零的非负向量z满足

从前面结论（Ⅰ）和（Ⅱ）的推证已知,存在 μ＞0，使得 μTA=ρ(A)μT。 由此,并利用式（5），有 μTz=λμTz。 注意到 μTz＞0,推出 λ=ρ(A),这与 λ≠ρ(A)的假设矛盾。因此结论（Ⅳ）成立。

[1]陈景良.特殊矩阵[M].北京:清华大学出版社,2001，76-93.

[2]罗家洪.矩阵分析引论：第三版[M].广州:华南理工大学出版社,2001：112-163.

[3]Henryk Mine.非负矩阵[M].杨尚竣，卢业广，杜吉佩，译.沈阳：辽宁教育出版社，1991：1-61.

[4]Pham Van At.Diagonal Transformation Methods for Computing the Maximal Eigenvalue and Eigenvector of a Nonnegative Irreducible Matrix[J].Lin.Aig.Appl,1991（6）：93-123.

[5]付文军.关于对角变换法计算不可约非负矩阵的最大特征值和相应特征向量的注解[J].内蒙古大学学报：自然科学版，1992，17（4）：317-324.

Abstrac：Based on the Perron theorem about eigenvalue of positive matrix and according to the relationship of positive matrix and irreducible nonnegative matrix,we extend the Perron theorem to irreducible nonnegative matrix and get some result about the Eigenvalue of irreducible nonnegative matrix.

Key words：positive matrix；irreducible nonnegative matrix；eigenvalue

On the Eigenvalue of Irreducible Nonnegative Matrix

YANG Kaifan
（Shanxi University of Technology,Hanzhong 723000）

O177.9

A

1673-1980（2012）02-0168-02

2011-11-09

陕西省教育厅基金项目(09JK380)

杨凯凡(1979-)，女，陕西乾县人，硕士,讲师，研究方向为算子理论。