陈根华 陈伯孝 杨明磊

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

米波雷达具有反隐身、抗反辐射导弹等方面的突出优势，但波束宽，角分辨率差等缺点限制了其实现高精度的目标跟踪与定位，因此如何提高米波雷达的测角精度与角分辨率具有重要意义。然而，无论采用单脉冲测角技术还是超分辨方法，阵列天线的物理孔径都是限制测角精度与角分辨率的重要因素之一，因此扩展孔径是提高测角精度的重要方法。最简单的扩展孔径技术就是增大阵元数，而阵元数的增加将直接导致系统的硬件成本和测角算法的计算复杂度的增加。由于米波雷达波长较长，架设密布的大孔径天线成本较高且工程实现困难，而早期微波合成的干涉雷达[1]可以有效扩展孔径提高测角精度且降低了系统的硬件成本，但是过小的自由度限制了测角模糊问题的解决。随着AESA(Active Electronically Scanned Array)技术的发展，Nilsson等人[2]首次提出了分布式阵列雷达的概念，大大的扩展了阵列的自由度。美国海军实验室也提出了将分布式子阵阵列天线应用于舰载多功能相控阵雷达的概念[3]，以提高雷达的探测性能与角度分辨率，同时降低成本与实现复杂度。MIT林肯实验室也提出了基于分布式相参合成阵列的新一代弹道导弹防御雷达系统[4]，通过多个分布式小孔径阵列来提高测角精度与分辨率，增强了雷达的威力，也提高了雷达系统的机动性。

由空域采样定理可知，对分布式阵列进行波束形成，将得到窄的主瓣及大量栅瓣的波束方向图，因此窄的主瓣提高了测角精度，栅瓣却导致了测角模糊。文献[3]提出对发射与接收波束方向图进行特定的设计来抑制栅瓣，但增加了系统实现的复杂度。而超分辨技术可以很方便地解模糊[2,5,6]，目前广泛应用的超分辨解模糊算法主要有双尺度法[7]、MUISC法与波束形成法[8]及具有自动解模糊功能的参数搜索最优化算法[9]。文献[9]介绍了基于最大似然法的分布式线阵的 DOA估计方法，该方法具有自动解模糊的功能，但其计算量较大，不易实现实时估计。Athley[10]分析了单个目标时分布式线阵的 DOA 估计性能的下界，但没有给出具体的方向估计方法。目前为止，分布式相参阵列的2维DOA估计方法未见报道。

针对以上问题，结合干涉雷达结构与2维方向估计方法，本文提出了一种扩展孔径的分布式相参米波阵列，分别在俯仰与方位上以干涉阵方式扩展孔径，在降低了硬件成本和测角的计算复杂度的同时，也提高了米波雷达系统的机动性。为了实现分布式阵列间的相参合成以扩展孔径，本文拟采用双尺度酉ESPRIT算法[11]及基于信号子空间与噪声子空间渐近正交特性的配对算法实现高精度无模糊的方向估计，最后从理论上用分段误差法(Method of Interval Error, MIE)[12]分析分布式阵列方向估计的门限效应，并给出分布式阵列填充系数门限和SNR门限的近似计算方法。仿真结果表明了分布式相参阵列有效地扩展了孔径，提高了测角精度，也表明了本文提出的2维DOA算法的有效性，及用MIE法分析分布式阵列性能的正确性与有效性。

2 数学模型

图1 分布式相参阵列示意图

设K个不相关的远场窄带信源入射到该分布式阵列上，(φk,θk)是第k个信源的方位角与俯仰角，y轴 和z轴 的 方 向 余 弦 分 别 为uk=cosθksi nφk,vk=s inθk,θk∈[-π/2,π/2],φk∈[0,2π],k=1,…,K。

将分布式阵列在采样时刻t的输出表示成两个数据列向量，即S1和S2组合得到的数据列xy(t)及S3得到数据列xz(t),t=1,…,N,

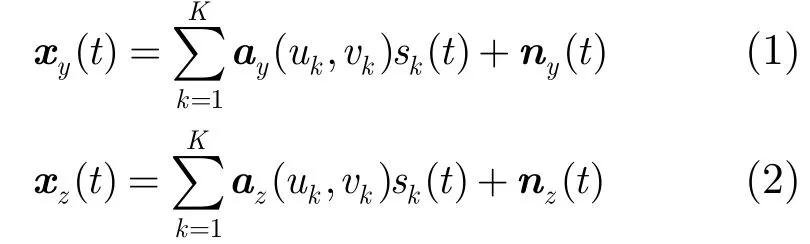
其中sk(t)为第k个信源复包络；ny(t)和nz(t)为与信号不相关的零均值、方差为的复高斯白噪声矢量，ay(uk,vk)为S1和S2的2NAyNAz维导向矢量，az(uk,vk)为S3的NEyNEz维导向矢量，

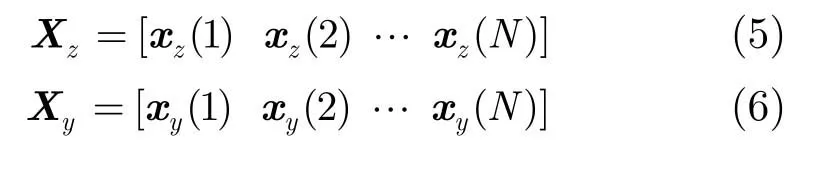
3 2维高精度DOA估计算法

在y轴方向上，S1和S2左边的NAy-1列与右边的NAy-1 列间具有偏移量为dy的空间移不变性，而S1和S2间具有偏移量为Dy的移不变性，因此称S1和S2间具有双尺度空间移不变性。类似地，在z轴方向上，S3和S4两个子阵上面的NEz-1行与下面的NEz-1 行间具有偏移量为dz的移不变性及子阵间偏移量为Dz的移不变性。由 ESPRIT算法可知，偏移量大的移不变性可得到精度高但周期模糊的方向余弦估计，而偏移量小的移不变性可得到精度低但无周期模糊的方向余弦估计[7,8]，因此可用粗估计为参考对精估计解模糊，且两个轴向的分布式阵列都是中心对称的，综合以上两个因素，本文选择2维的双尺度酉ESPRIT算法估计信源的方向余弦[7,11]。

其中

3.1 方向余弦的粗估计与精估计

在y轴方向上，S1和S2左边的NAy-1列和右边的NAy-1列分别构成了两个完全相同的子阵。由于S1和S2所有阵元信息的充分利用有利于提高信噪比和物理孔径的充分利用，因此S1和S2的偏移量为dy的空间移不变性可以表示为

由酉ESPRIT算法[12]可得，y轴方向上偏移量为dy的旋转不变性可表示成

类似地，y轴方向上偏移量为Dy的旋转不变性可表示成

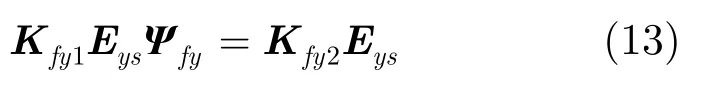
根据最小二乘法，y轴方向偏移量为dy和Dy的实值旋转矩阵分别为

同理，可得z轴方向上偏移量为dz和Dz的实值旋转矩阵分别为

对以上的旋转矩阵进行特征值分解后，可得方向余弦的粗估计与精估计，但顺序是任意的。由于旋转矩阵为实值矩阵，因此可用自动配对算法[11]来实现方向余弦的粗估计与精估计间配对，即

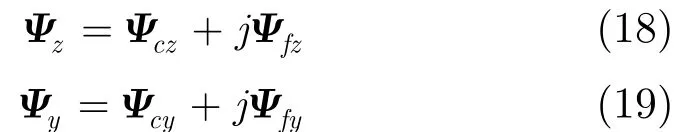
从而得到正确配对的粗估计与精估计，即

3.2 解模糊

由于基线Dy和Dz都远大于子阵孔径，方向余弦精估计可能是周期模糊的，因此需对精估计解模糊，常用的解模糊算法主要有双尺度法[7,8]，MUSIC法[9]及常规波束形成法[9]，其中MUSIC法与波束形成算法的计算量较大，而双尺度法的计算量较小，易于实时实现，因此本文选择双尺度法对方向余弦精估计解模糊。

由双尺度解模糊方法可得到高精度无模糊的方向余弦精估计，即

其中

依据上述理论，可实现类别数的自动判别，确定K后，结合FCM算法可实现像素类别的归属完成影像分割.具体的操作流程总结如下：

3.3 方位角与俯仰角的配对

常用的配对算法有穷尽搜索法[9]、置换矩阵法与相关矩阵法[14]，其中穷尽搜索法配对成功概率最高，因此本文采用基于信号子空间与噪声子空间渐近正交特性的穷尽搜索配对算法实现方位角与俯仰角的配对[15]，即

解式(23)便可得属于同一信源的两个方向余弦分量，从而求出信源的方位角与俯仰角

4 分布式阵列方向估计的门限效应

分布式阵列波束方向图的栅瓣结构类似于分段检测问题[12]。如果能够正确解模糊，在一定SNR条件下，则通过增加基线长度可提高方向估计的精度，然而当基线长度超过某个门限时，正确解模糊概率将迅速降低，使得估计精度迅速降低，从而呈现出基线模糊门限效应[10,12]。而基线长度一定时，当SNR低于某个门限值时，正确解模糊概率也将迅速降低，也呈现出SNR门限效应。因此分布式阵列的方向估计性能具有基线模糊门限与SNR门限效应，下面从理论上对此进行分析。

其中erfc(·)为补误差函数，L表示栅瓣的个数，BI表示分布式阵列粗估计的克拉美劳下界(CRB)[10]，且其中N表示快拍数。

由MIE法可得方向余弦u0估计的MSE，即

其中BC表示分布式阵列方向余弦精估计的CRB[10]，且

下面用 MIE法分别给出基线模糊门限与 SNR门限的近似计算方法。令 ∂V ar()/∂Dy=0，解该方程即可求出一定SNR条件下的基线模糊门限，从而得到分布式阵列的填充系数门限。由于该方程的直接求解很复杂，本文采用近似的方法来求解。在模糊门限处，只有主瓣与第1栅瓣对总的均方误差贡献最大，并利用补误差函数的近似式[12]

因此式(28)可近似为

式(31)对Dy求导，并令其等于0，即

由式(32)难以得到基线门限的闭式解，可由仿真计算给出。

通常SNR门限定义为均方误差比CRB高3 dB时所对应的SNR[12]，因此由式(31)可得

分别将式(27)和式(29)代入式(33)后，即可用数值方法得到分布式阵列的SNR门限。

以上两个方法可近似计算出分布式阵列的填充系数门限和SNR门限。在设计分布式阵列时，需要对填充系数与SNR进行综合考虑，使得正确解模糊的概率足够高，以实现分布式阵列孔径的相参合成和孔径扩展，从而提高方向估计的精度。

5 仿真结果与分析

设NAz=NEz=NEy=4,NAy=8,dy=dz=λ/2，分布式相参阵列总的阵元数为 80。每个数据点做300次Monte Carlo试验，快拍数N为100，信噪比SNR定义为阵元信噪比。

试验1验证分布式阵列方向估计的高精度性能及本文的2维方向估计算法的有效性。本次试验选择具有相同阵元数的8行10列的均匀长方形面阵(URA)与分布式阵列的比较。假设等功率的两个信源，且入射方向分别为(φ1,θ1)=(30°, 20°),(φ2,θ2)=(31.5°, 17.5°), FFE=0.33, FFA=0.25。如图2所示，分布式阵列的联合方向估计曲线上存在明显的门限效应[12]，且SNR门限约为1 dB，而URA阵列却不存在该现象。当SNR高于门限时，分布式阵列的方向估计精度比URA阵列约高5倍，而当SNR低于门限时，精估计的正确解模糊概率迅速降低，分布式阵列的方向估计精度低于URA，趋近于粗估计的精度，因为粗估计时采用的物理孔径要小于URA，也说明了当 SNR小于门限时精估计的正确解模糊概率将趋于0，而SNR门限与阵列填充系数直接相关，试验3和试验4将详细地分析该问题。

试验2比较各种解模糊算法的性能。设方位维填充系数FFA=0.24, 2个信源的仿真条件同试验1。如图3所示，3种解模糊算法都具有明显的门限效应。双尺度法的SNR门限比其他两种方法要高的多。因为 MUSIC算法与常规波束形成算法都是直接对精估计解模糊，不需要粗估计做参考，且两者的正确解模糊概率要高于双尺度法[9]。明显地，高的正确解模糊概率是以大的计算量为代价的，因为MUSIC算法与常规波束形成算法的计算量要远远大于双尺度法。而在高SNR时，3种算法的性能是相当的。

试验3分析填充系数与方向估计精度间的关系。在分析方位角估计精度与FFA间的关系时，设FFE=0.33，两个信源仿真条件同试验1。由图4(a)可知，随着FFA的逐渐减小，即基线逐渐增加，栅瓣间隔逐渐减小，在一定的填充系数范围内，方位角估计精度逐渐提高，但当填充系数约低于0.2时，估计精度迅速恶化，正确解模糊概率迅速降低，此时的填充系数值称为填充系数门限。同时，FFA门限随 SNR的增加而减小，SNR越高，FFA的门限越低。由图4(a)可知，在SNR=-2 dB时，FFA门限约为0.2。由图4(b)可知，仰角估计精度与FFE间也具有类似关系。试验3得到的仿真结果与前文的理论分析是一致的。本文所分析的分布式阵列结构中俯仰孔径与方位孔径间并没有产生耦合，而在舰载或机载平台上时，分布式阵列的布阵一般会受到平台结构特征限制，则应尽量防止分布式孔径间产生耦合且填充系数应该高于0.2，并通过计算机仿真选择分布式阵列的最优填充系数，同时在填充系数与SNR间折衷考虑，从而实现分布式阵列孔径间的相参合成及孔径扩展，使得分布式阵列测角性能最优。

图2 分布式阵列的联合方向估计精度

图3 3种解模糊算法性能比较

图4 填充系数与方向估计精度间的关系

试验4用 MIE近似法验证分布式阵列的填充系数门限与SNR门限。图5(a)为不同SNR条件下方向余弦u估计的均方根误差与FFA间的关系图。由图可知，CRB确实没有考虑栅瓣产生的模糊误差[10,12]，而MIE近似法能较好的说明方向余弦估计精度与FFA间的关系，且当SNR=2 dB时FFA门限约为0.2左右，与试验3仿真结果一致。因此可得出结论：分布式阵列的填充系数门限随着SNR的提高而减小。图5(b)所示为不同FFA下，由MIE近似法得到的SNR门限，当FFA分别为0.25, 0.18时，对应的SNR门限约为-5 dB,-2 dB，由此可知，分布式相参阵列的 SNR门限随着填充系数的减小而提高。

以上仿真结果充分说明了分布式相参阵列有效地扩展了孔径，提高了测角性能，同时也从理论上验证了分布式阵列方向估计时存在的 SNR门限与填充系数门限。

6 结论

针对米波雷达波束宽及测角精度低等问题，同时也为了降低硬件成本及实现复杂度，提高米波雷达系统的机动性，本文提出了一种扩展孔径的分布式相参阵列，并根据该阵列所具有的双尺度空间移不变性及中心对称性，采用双尺度酉ESPRIT算法及基于信号空间与噪声空间正交特性的配对算法实现方位角与仰角的高精度估计方法，并且采用MIE法分析分布式阵列方向估计的门限效应，并给出了分布式阵列的填充系数门限与 SNR门限的近似计算方法。仿真结果验证了分布式相参阵列方向估计的高精度性能及本文提出的2维方向估计算法的有效性，同时也验证了分布式阵列方向估计存在填充系数门限与SNR门限，且与MIE近似法的结论一致。因此在设计分布式阵列时，应根据SNR选择最优的填充系数，使分布式阵列的测角性能最优。本文采用的双尺度ESPRIT算法可在方位与俯仰并行运行，增强了算法的实时性，非常适合工程应用。总之，通过分布式的多个小孔径间相参处理可有效扩展阵列孔径，不仅提高了雷达的测角精度与分辨率，而且降低了硬件成本并提高了系统的机动性。

图5 MIE近似法验证分布式阵列的填充系数门限与SNR门限

[1]Jacobs E and RALSTON E W. Ambiguity resolution in interferometry[J].IEEE Transactions on Aerospace and Electronic Systems, 1981, 17(6): 766-780.

[2]Nilsson E and Warston H. Radar with separated subarray antennas[C]. 2003 Radar Conference, Adelaide, Australia,2003: 194-199.

[3]Lin Chih-heng. Distributed subarray antenna for multifunction phased array radar[D]. [Master dissertation],Monterey, California: Naval Postgraduate School, 2004.

[4]Coutts S, Cuomo K, McHarg J,et al.. Distributed coherent aperture measurements for next generation BMD Radar [C].IEEE Sensor Array and Multichannel Signal Processing Workshop, Massachusetts, USA, 2005: 390-393.

[5]Chen W, Xu X, Wen S,et al.. Super-resolution direction finding with far-separated subarrays using virtual array elements[J].IET Radar,Sonar&Navigation, 2011, 5(8):824-834.

[6]Blunt S D, Chan T, and Gerlach K. Robust DOA Estimation:the reiterative superresolution(RISR)algorithm[J].IEEE Transactions on Aerospace&Electronic Systems, 2011, 47(1):332-346.

[7]Yang Xue-ya and Chen Bai-xiao. An eigenstructure-based 2D DOA estimation method using dual-size spatial invariance array[J].Science China,Part F, 2011, 54(1): 163-171.

[8]Zoltowski M D and Wong K T. Closed-form eigenstructurebased direction finding using arbitrary but identical subarrays on a sparse uniform Cartesian array grid[J].IEEE Transactions on Signal Processing, 2000, 48(8): 2205-2210.

[9]Engdahl C and Sunnergren P. Model-based adaptive detection and DOA estimation using separated subarrays [C].2002 IEEE Radar Conference, Long Beach, California, USA,2002: 104-109.

[10]Athley F. Direction-of-arrival estimation using separated subarrays[C]. The 34th Asilomar Conference on Signals,Systems, and Computer, Pacific Grove, California, USA,2000: 585-589.

[11]Zoltowski M D, Haardt M, and Mathews C P. Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT[J].IEEE Transactions on Signal Processing, 1996, 44(2): 316-328.

[12]Van Trees H L. Detection, Estimation, and Modulation Theory, Part I, Detection, Estimation and Linear Modulation Theory [M]. New York: Wiley&Sons, 2002: 277-284.

[13]杨雪亚, 陈伯孝. 基于实值特征子空间迭代的DOA估计算法[J]. 西安电子科技大学学报, 2010, 37(2): 242-247.

Yang Xue-ya and Chen Bai-xiao. Novel method for DOA estimation of coherent signals by eigen-subspace iteration[J].Journal of Xidian University, 2010, 37(2): 242-247.

[14]Liang Jun-li and Liu Ding. Joint elevation and azimuth direction finding using L-shaped array[J].IEEE Transactions on Antennas and Propagation, 2010, 58(6): 2136-2141.

[15]Hua Y B, Sarkar T K, and Weiner D. An L-shaped array for estimating 2-D directions of wave arrival[J].IEEE Transactions on Antennas and Propagation, 1991, 39(2):143-146.