基于改进粒子群算法的船舶排样问题研究

2012-06-30杜浩楠黄泽峰黄泰安

江苏船舶 2012年6期

杜浩楠，黄泽峰，袁雁，黄泰安

(1.江苏科技大学南徐学院，江苏镇江 212003;2.江苏科技大学计算机科学与工程学院，江苏镇江 212003)

0 引言

在船舶行业逐渐萧条的形势下，最大限度的降低生产成本是提高船厂效益的有力途径。造船材料占据了生产成本的很大部分，因此提高船舶板材的利用率是关键。然而，船舶零件多为不规则形状，给计算机自动排样程序的实现增加了困难。一些学者就通过矩形包络的方法，将不规则图形排样转化为矩形件排样，这样更利于问题的解决。矩形件排样问题在理论上属于具有最高复杂性的NP完全问题，随着矩形零件的增多，很难用传统算法得到最优解。因此，不管是从理论研究还是从实际应用上讲，对二维矩形件排样问题的研究都具有重要的意义。

粒子群优化算法［1］(Particle Swarm Optimization，简称PSO)是由Kennedy和 Eberhart首先提出的一种全局随机搜索算法。它模拟鸟群觅食过程中的迁徙和群聚行为，利用群体智能搜索出较好的解。该算法有着收敛速度快、设置参数少、算法简单易实现等优点，所以一经提出就受到了学术界的广泛重视，并被广泛应用于函数优化、模式分类、模糊系统控制、神经网络训练以及其他工程领域中［2，3］。因此近年来许多国内外学者研究粒子群算法，并提出了很多改进的算法［4～8］。

要使矩形件优化排样获得更好的效果，可考虑从2方面入手:一是用更好的方法确定矩形件排放的先后顺序和排放方式，二是设计出更好的矩形件排放算法［9］。国内外不少学者已经做了很多研究工作，提出了一些近似算法和启发式算法［10～13］。本文从第一方面入手，应用改进的粒子群算法——蛙跳简化粒子群算法进行矩形件优化排样。排样实例表明了该方法的有效性。

1 剩余矩形法简介

对于矩形件排样问题，常见的启发式算法有左底算法(BL算法)、左底填充算法(BLF算法)、下台阶法、最低水平线法、剩余矩形法［14，15］。本文是将改进的粒子群算法同剩余矩形法相结合用于排样问题，剩余矩形法可做如下阐述:

参照图1，宽W、高H的矩形(0，0，W，H)。一个矩形件i(宽wi、高hi)加入后，原来的大矩形减去加入矩形件的位置。设矩形件的左下角坐标为(xi，yi)，则大矩形减掉与矩形件(xi，yi，xi+wi，yi+hi)相交的部分后，得到的4个新的矩形:(0，0，xi，H)、(0，0，W，yi)、(0，yi+hi，W，H)、(xi+wi，0，W，H)。相邻矩形件的重叠部分如何处理将在后文中给出。

剩余矩形法包含剩余矩形集、待排矩形集、已排矩形集等3个矩形集。剩余矩形集包含任何没有被排样的空间，待排矩形集和已排矩形集分别包含待排、已排的矩形件信息。剩余矩形法可作如下描述:

(1)初始时，剩余矩形集为母板(0，0，W，H)。

(2)当1个矩形件排入时，3个集都要进行更新。待排矩形集要删除代表该矩形件的结点。在剩余矩形集中找到一个能放下该矩形件的最小剩余矩形，将该矩形件放置在此剩余矩形的左下角(满足BL条件)，删除此剩余矩形，得到了2个新的剩余矩形R1和R2，如图2所示。对于R1和R2的重合部分(图中虚线部分)，将在第3步进行调整。对于已排矩形集，则记录排入矩形的位置。

图1 剩余矩形法示意图

(3)更新剩余矩形集。新的剩余矩形的产生会引起剩余矩形集发生变化，这时就要对剩余矩形集作如下调整:对于有完全包含关系的剩余矩形，删除被包含的矩形，仅保留较大面积矩形;对于有相交关系的剩余矩形，全部保留;对于与已排入矩形有相交关系的剩余矩形，全部删除;对于面积为零或已放不下剩下任一矩形的剩余矩形，全部删除。按此规则更新的剩余矩形集用于下一次排样。

(4)重复第2、第3步，直至所有矩形排完，即待排矩形集为零，输出板材利用率。

从上面的描述可以看出，剩余矩形法既满足BL条件又符合BLF算法的思想，这样就能够对排样过程中产生的空白间隙进行填充，保证了板材较高的利用率，有利于找到较优解。

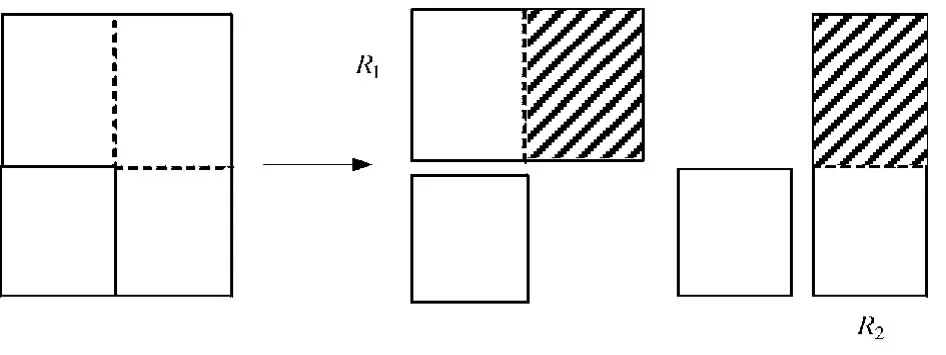
图2 剩余矩形法切割示意图

2 粒子群算法的改进

蛙跳简化粒子群算法(SFLA-SPSO)就是将混合蛙跳算法的分组思想引入到文献［8］给出的简化粒子群算法中。由于多了一个分组操作，将原来简化的粒子群算法的位置更新公式改写如下:

式中:x(t)、x(t+1)分别表示粒子当前位置和迭代后的位置。符号右边的第1项为“历史”部分，表示过去对现在的影响，通过惯性因子w来调节影响程度;第2项为“认知”部分，表示粒子对自身的思考，c1为自身学习因子，Pbest表示粒子自身最优位置;第3项为“社会”部分，表示粒子与组内最优粒子gbest的比较和模仿，c2为组内学习因子;第4项为“超社会”部分，表示粒子与总的粒子群体最优粒子g′best的比较和模仿，c3为全局学习因子;r1、r2、r3均为［0，1］之间的随机数，由计算机分别随机生成。这样粒子就获得了更为丰富的信息来更新自身位置，局部信息和全局信息能够得到充分利用，粒子间的信息共享和合作也更加充分。

蛙跳简化粒子群算法的具体流程如下:

Step 1选定粒子群规模(m组，每组n个粒子)，对粒子群的初始位置进行初始化;

Step 2计算每个粒子的适应度;将粒子按照适应度函数值由小到大的顺序进行排序，得到全局最优值;

Step 3对粒子进行分组，第 i组粒子为{xi，xm+i，x2m+i，…，x(j－1)m+i}，i∈［1，m］，j∈［1，n］;

Step 4对于每个粒子，将其适应度与所经历过的最好位置的适应度进行比较，如果更好，则将其作为粒子的个体历史最优值，用当前位置更新个体历史最好位置pbest;

Step 5选出组内最优位置gbest，对于第i组粒子，有gbest=xi;

Step 6每个小组中n个粒子按照公式(1)更新自身位置，迭代完成后对每个粒子按适应度由小到大的顺序进行排序，排序后的粒子进入下一次组内迭代，转到Step 5;

Step 7达到组内迭代次数后，各组更新后的粒子进入下一次分组，转到Step 3;

Step 8达到分组次数后，退出。

蛙跳简化粒子群算法的流程图如图3所示。

3 改进粒子群算法在船舶排样中的应用

蛙跳简化粒子群算法定义于连续的函数空间，要将其应用到组合优化问题中，必须将其改造为离散的算法。参照文献［16］，本文求解矩形件排样问题的蛙跳简化粒子群算法作如下定义:

3.1 基本概念

(1)粒子群

粒子群表示待排矩形件部分排样序列(包含是否翻转的信息)的集合。

(2)粒子位置

一个排样序列 X=(r1N1，r2N2，…，rnNn)代表了一个粒子的位置，即排样问题的一个解。其中，Ni为矩形件的序号;ri为翻转因子，只取1或－1，ri=1表示矩形件Ni横放，ri=－1表示矩形件Ni竖放。粒子的位置随着搜索的进行而不断改变，即排样序列在不断发生变化。

图3 蛙跳简化粒子群算法流程图

例如 X=(1，2，－5，3，－4)就是一个位置，表示先横放1号矩形件，接着横放2号矩形件，竖放5号矩形件，横放3号矩形件，最后竖放4号矩形件。

(3)置换子

假设某个粒子k的位置为Xk，置换子(riik，rjjk)的操作定义为交换Xk中序号为ik和jk的矩形件位置，并继承置换子中的翻转因子。即 X′k=Xk+(riik，rjjk)，其中X′k为粒子 k经过置换操作后的新位置。

例如:Xk=(3，2，－1，5，4)，(ik，jk)=(1，－2)，表示先将排样序列(3，2，－1，5，4)中1号矩形件横放，2号矩形件竖放，再调换两者的位置，则X′k=(3，2，－1，5，4)+(1，－2)=(3，1，－2，5，4)。

(4)置换序列

一个或多个置换子组成的队列即为置换序列，它表示置换子按队列顺序依次作用在粒子位置上。((4，－1)，(2，－3))就是一个置换序列，它由置换子(4，－1)、(2，－3)组成，表示先把矩形件4横放，矩形件1竖放，然后交换位置，再将矩形件2横放，矩形件3竖放，再将位置进行互换。

例如:粒子位置(4，－2，－5，1，3)与置换序列((4，－1)，(2，－3))的操作

(4，－2，－5，1，3)+((4，－1)，(2，－ 3))=((4，－2，－5，1，3)+(4，－1))+(2，－3)=(－1，－2，－5，4，3)+(2，－3)=(－1，－3，－5，4，2)。

(5)粒子间距

粒子间距(粒子间的距离)就是一个置换序列，它表示粒子从一个位置更新到另一个位置需要的置换子的队列。用D表示间距，|D|表示间距长度即间距所含置换子的数目。间距D可以表示为:

3.2 基本操作

(1)+(位置，间距)

粒子位置与粒子间距相加，表示一组置换子序列依次作用于粒子位置上，粒子到达一个新的位置。

例如:A=(－2，－3，1，4，5)+(－1，4)=(－2，－3，4，－1，5)。

(2)－(位置，位置)

粒子的位置与位置相减，即得到粒子间距(置换序列)。

例如:A=(1，4，5，2，3)，B=(1，4，－2，－3，5)，分别比较A(i)和B(i)，找到第一个A(i)≠B(i)的位置，即A(3)=5，B(3)=－2，则第一个置换子为(A(3)，B(3))即(5，－2)，更新 B=B+(5，－2)=(1，4，5，－3，－2);同理，A(4)≠B(4)，第二个置换子为(2，－3)，更新 B=B+(2，－3)=(1，4，5，2，－3);A(5)≠B(5)，第三个置换子为(3，－3)，更新 B=B+(3，－3)=(1，4，5，2，3)，此时 A=B。最后得到 A－B的置换序列为((5，－2)，(2，－3)，(3，－3))。即A－B=D，则 A=B+D。

设定i=1，j=0，n为 A、B两个序列的长度，即待排矩形件的个数。Dj表示A－B得到的置换序列中第j个置换子。A－B具体过程如下:①若A(i)=B(i)，则 i=i+1;否则 j=j+1，Dj=(A(i)，B(i))，i=i+1，同时更新B=B+Dj;②重复执行①，直到i＞n时退出。A －B={Dj，j=1，2，…}。

(3)⊕(间距，间距)

粒子间距与间距相加，表示把一个间距加到另一个间距末尾。如:((5，－2)，(3，－3))+((4，－1)，(2，－3)，(3，5))=((5，－2)，(3，－3)，(4，－1)，(2，－3)，(3，5))。

(4)×(实数，间距)

间距与实数相乘，例如:cD，c为实数，D为间距。假设间距D的长度为k，乘法操作其实就是截取间距列表，使得新的间距的长度等于［ck］。例如c=0.8，k=6，则运算的结果是截取间距的前4个置换子;若c≥1，则取全部(即8个)置换子。

3.3 粒子更新公式定义

算法的粒子更新公式为:

3.4 适应度函数

本文在定宽无限长的板材上进行排样。设板材宽度为W，第i(共有n个矩形件，i=1，2，…，n)个矩形件的长为li，宽为wi。矩形件沿板材长度方向进行排放，则优化排样的适应度函数为:

式中:h为零件排样后在板材上所达到的最大高度，则理论最优高度为Hbest=max∑ni=1liwi/W，适应度函数可更新为E=Hbest/h。

3.5 终止条件

算法在达到最大迭代次数时停止。

3.6 算法步骤

算法步骤同蛙跳简化粒子群算法的步骤，只是在计算适应度函数时要调用剩余矩形法的程序。

4 排样实例测试及结果分析

本文分别对2组矩形件进行测试，测试数据见表1。实验中c1=c3=2，c2=0.8;第1组粒子群分为5组，每组5个，第2组粒子群分为5组，每组10个;组内迭代次数为1，分组次数为30;程序独立运行50次，取最高利用率对应的排样序列进行作图。因矩形件参数均为整数，故理论最低高度H′best=(Hbest)+1，此时理论最高利用率为 E′best=Hbest/H′best。2组矩形件用本文算法得到的最优排样图分别如图4、图5所示。

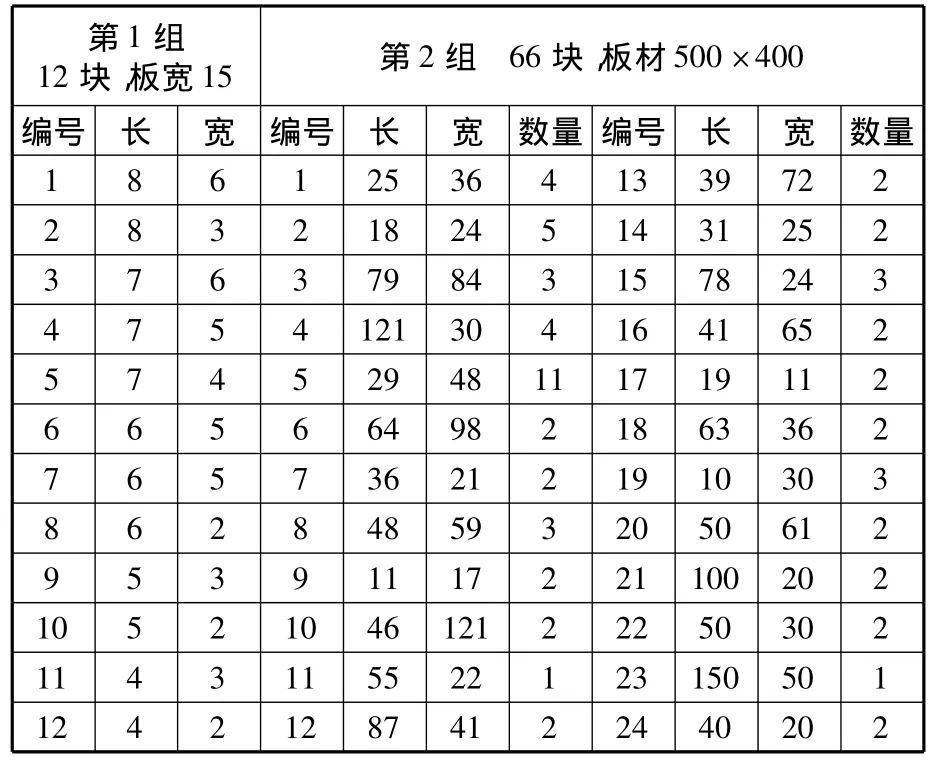
表1 测试数据

由图4、图5可以看出，在板材宽带为15的情况下，12块矩形件排样计算出的最低高度为20，此时板材利用率为98%，排样图已达到最优结果;66块矩形件排样计算出的最低高度为318，此时板材利用率为90.61%，优于文献［9］的排样结果(利用率88.12%)。总体来看，基于蛙跳简化粒子群算法的矩形件排样效果较好，也证明了该算法的有效性。

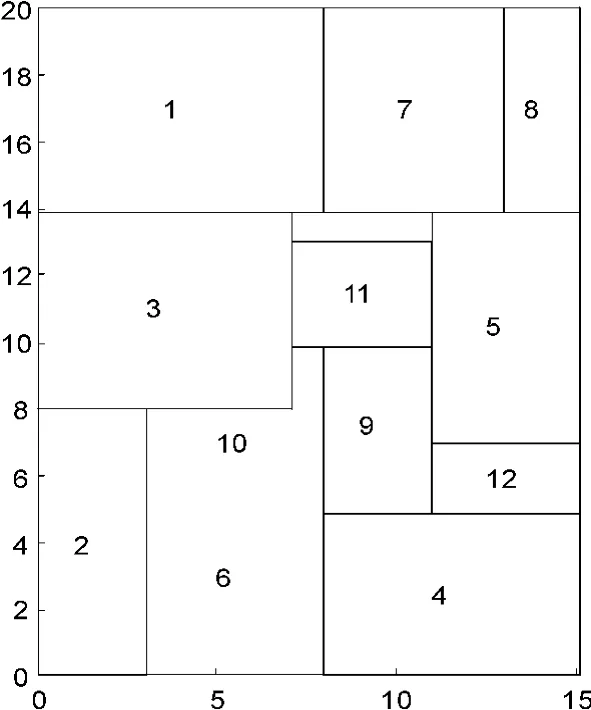
图4 12块矩形件排样结果

图5 66块矩形件排样结果

5 结论

船舶零件属于不规则形状物体，可用组合、矩形包络等方式将其转化为矩形件再进行排样［17］。本文将蛙跳简化粒子群算法经离散化后，结合剩余矩形法来求解定宽无限长板材上的矩形件排样优化问题。文中将矩形件的翻转信息加入到排样序列中，降低了程序的复杂度，提高了运行效率。2个测试实例表明，此种求解的算法能找到比较满意的排样方案，说明了此种排样方法的有效性。然而，由于剩余矩形法是将矩形件一块一块排入板材中，这样得到的排样图形有些杂乱，不方便切割，给实际的工程应用带来了困难。如何实现同规格矩形件组合后按块排入是本文下一步研究的重点。

［l］Kennedy J，Eberhart R C.Particle swarm optimization［C］//Proc.IEEE Int＇I Conf.on Neural Networks.NJ Piscataway，IEEE Press，1995:1942－1948.

［2］Eberhart R C，Shi Y.Particle Swam Optimization:Development，Applications and Resources［C］//Proc.Congress on Evolutionary Com-putation.Korea:IEEE Serrice center，2001:8l－86.

［3］柯晶，钱积新.应用粒子群优化的非线性系统辨识［J］.电路与系统学报，2003，8(4):12－15.

［4］孙湘，周大为，张希望.惯性权重粒子群算法模型收敛性分析及参数选择［J］.计算机工程与设计，2010，31(18):4068－4071.

［5］石永生，陈家琪.基于高斯变异的量子粒子群算法［J］.电脑与信息技术，2010，18(6):9－12.

［6］王华秋，曹长修.基于模拟退火的并行粒子群优化研究［J］.控制与决策，2005，20(5):500－504.

［7］徐志烽.一种多粒子群的协同优化算法［J］.现代电子技术，2007，(1):131 －133.

［8］胡旺，李志蜀.一种更简化而高效的粒子群优化算法［J］.软件学报，2007，18(4):861－868.

［9］黄红兵.矩形件排样问题的粒子群算法求解［J］.机械工程师，2007，(12):60－61.

［10］杨传华，等.定序列矩形件优化排样的二维搜索算法［J］.佳木斯大学学报:自然科学版，2010，28(3):354－356.

［11］陶献伟，王华昌，李志刚.基于填充算法的矩形件排样优化求解［J］.中国机械工程，2003，14(13):1104－1107.

［12］李明，周泽槐.基于粒子群算法的矩形件优化排样［J］.电路与系统学报，2007，12(2):39－42.

［13］李妮.基于遗传算法的矩形件排样问题研究［D］.太原:山西大学，2010.

［14］陈钊.求解矩形排样问题的离散粒子群算法［D］.合肥:合肥工业大学，2009.