王俊杰, 王连堂, 杨宽德

(1.思茅师范高等专科学校,云南普洱665000;2.西北大学数学系,陕西西安710127)

0 引言

许多物理问题经常需要用非线性偏微分方程(NPDEs)描述。研究非线性偏微分方程的精确解是数学物理的一个重要课题。非线性薛定谔方程在非线性物理学中具有非常重要的意义,作为描述波包在弱非线性介质中传播的普遍方程,它出现在物理和应用数学的许多分支中,包括等离子体物理、非线性光学、凝聚态物理等。因此寻找非线性薛定谔方程的精确解,尤其是它的孤立子解[1-5],一直是数学家和物理学家们非常感兴趣的课题。近年来,科学家已经建立许多新的方法,逆散射法[6]、Hirota变换法[7]、tanh函数展开法[8]、齐次平衡法[9]、分离变量法[10]、sin-cosine函数展开法[11]、Jacobi椭圆函数展开法等[12-13]。

在文献[14]中对下面非线性薛定谔方程：

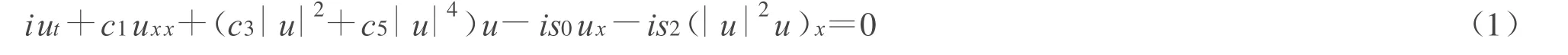
已经做了一些研究。考虑下面具有任意阶的非线性薛定谔方程：

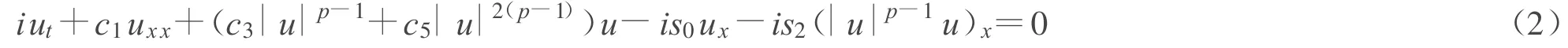
其中p是一个大于1的整数。

利用行波变换和辅助函数法把具有任意阶非线性薛定谔方程最终转化为一个非线性常微分方程的解,通过对这个微分方程的研究可以得到具有任意阶非线性薛定谔方程的更多的孤立波解、三角孤立波解、扭孤立波解。在生活中,可以利用这些解来解释一些非线性物理现象。

1 辅助方程的计算

对于任意一个非线性方程可以表示成下面的形式：

可以寻求它的行波解：

把式(4)带入(3)可以得到下面非线性常微分方程：

假设上面的方程(5)可以表示为下面形式：

令函数w(ξ)满足下面的辅助方程：

把式(6)和式(7)代入式(5),根据齐次平衡法的思想,为使方程(5)中的非线性项和最高阶导数相平衡,可以确定方程(6)中的参数n。

把式(6)和式(7)代入式(5),使 wiw′j(i=0,1,2,…;j=0,1)系数全为零,将得到一个非线性代数方程.通过求解这个非线性代数方程,可以得到参数c,ai,hj(i=0,…,n,j=0,2,4)。

2 具有任意阶非线性薛定谔方程的包络行波解

为了求解任意阶非线性薛定谔方程(2),寻求它的包络行波解为：

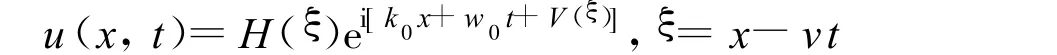
其中k0,w0,v为任意常数。从而有：

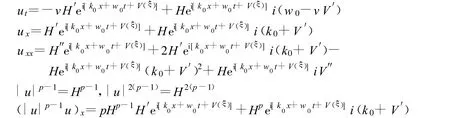
代入方程(2),消掉 ei[k0x+w0t+V(ξ)]得 ：虚部：

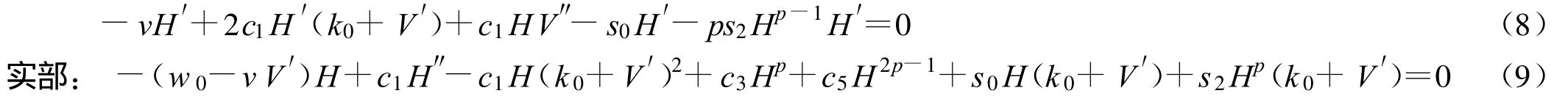
所以把问题(2)转换为问题(8～9)的耦合非线性偏微分方程组,但求解(8～9)的耦合非线性偏微分方程组仍然非常困难。所以假设函数 V,H满足：

将式(10)代入式(8)得到：

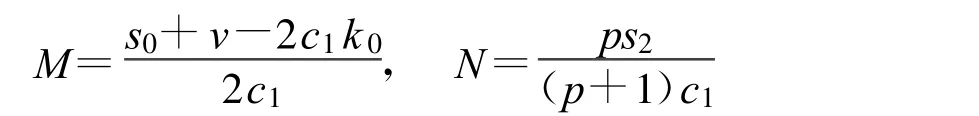
将式(10)代入式(9)最终得到：

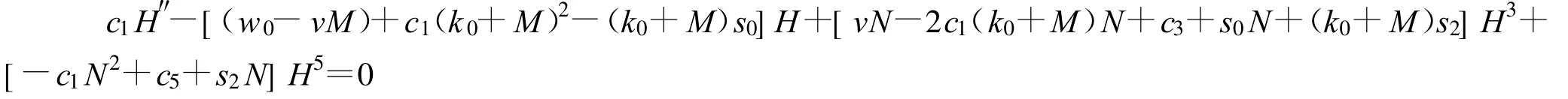
整理可得：

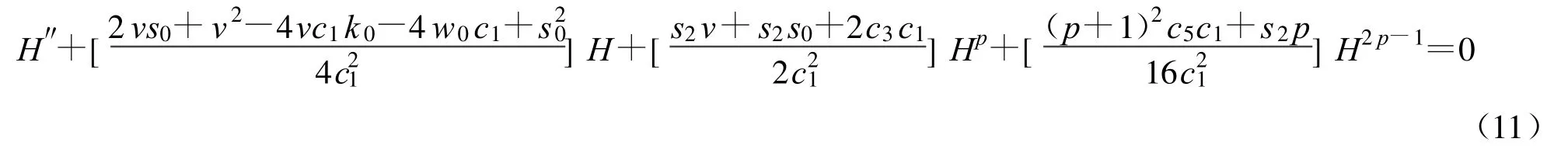
令：

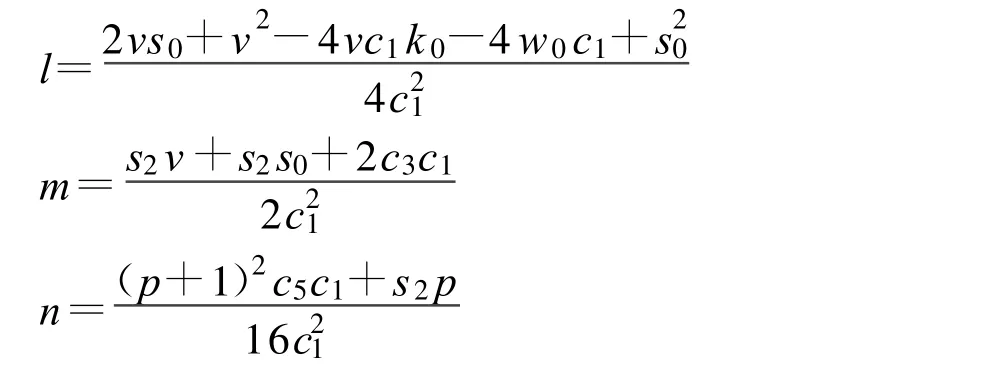
最终把非线性薛定谔(2)转化为如下任意次强非线性项的Lienard方程：

做变换：

代入方程(12)可以得到：

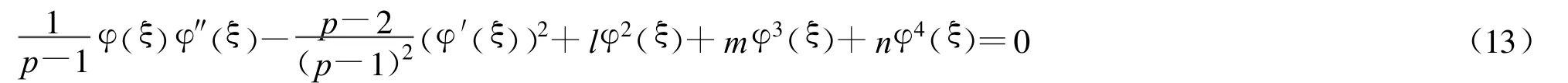
φ写成式(6)的形式,根据齐次平衡法的思想,为了使式(13)中的 φ(ξ)φ″(ξ),(φ′(ξ))2,φ4(ξ)相平衡 ,可以得到n=1

把式(14)、(7)代入式(13)可以得到：

令式(15)中的各次幂的系数等于0,得到代数方程组：

可以得到上面方程组的解：

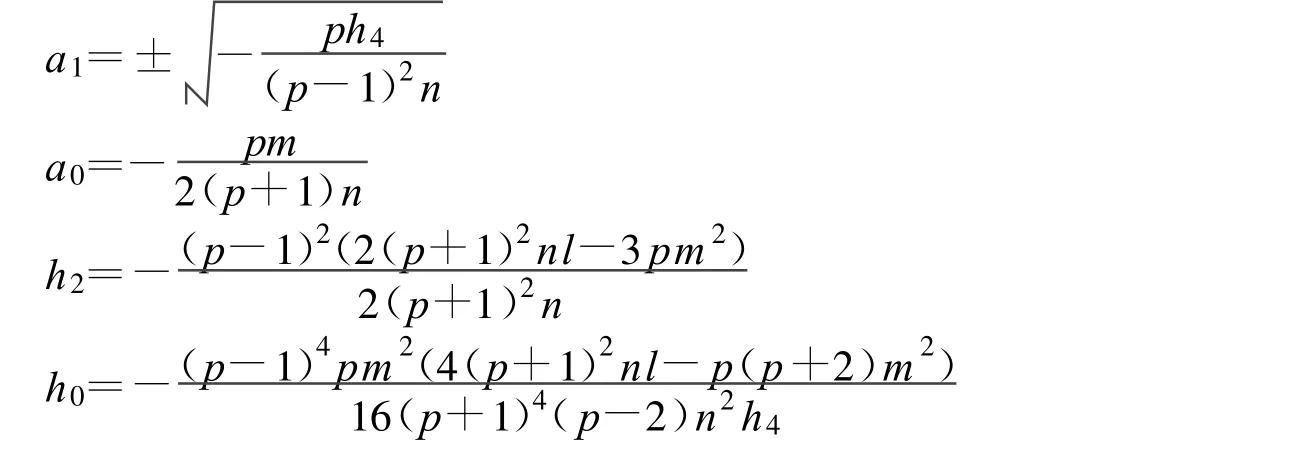
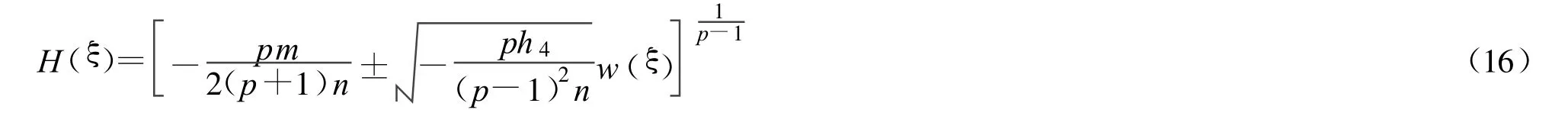
其中

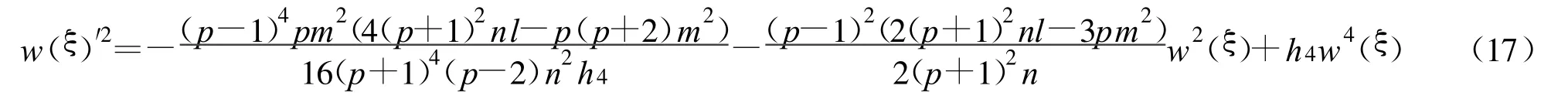
对于辅助方程(7)可以选择不同 p,m,l,n,h0,h2,h4得到方程(2)的孤立波解、三角孤立波解、扭孤立波解、Jacobi椭圆函数解,在文献[14]中,已经给出了方程(1)的孤立波解、三角孤立波解、扭孤立波解,但是没有给出Jacobi椭圆函数解。

情形1(孤立波解,三角孤立波解)

定理1 假设4(p+1)2nl-p(p+2)m2=0,h4=

(i)如果h4＜0,方程(2)有一孤立波解：

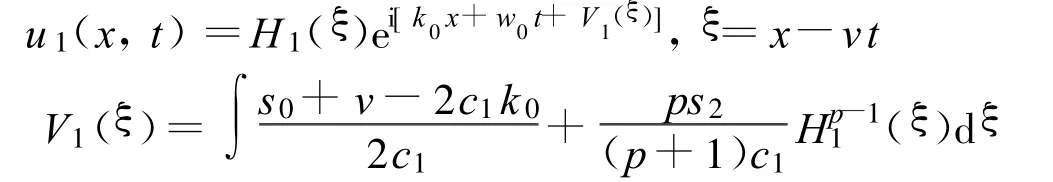
(ii)如果 h4＞0,方程(2)有一三角孤立波解：

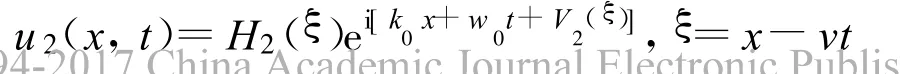
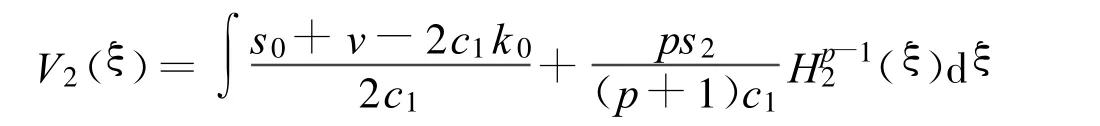
其中

定理2 假设 m=0,h4=(p-1)2l

(i)如果h4＞0,方程(2)有一孤立波解：

(ii)如果 h4＜0,方程(2)有一三角孤立波解：

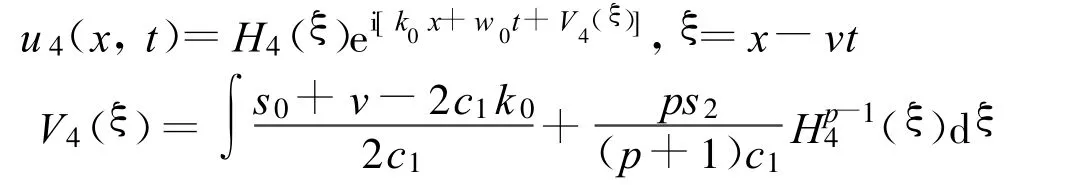
其中：

情形2(扭孤立波解)

定理3 假设

如果l＞0,方程(2)有一扭孤立波解：

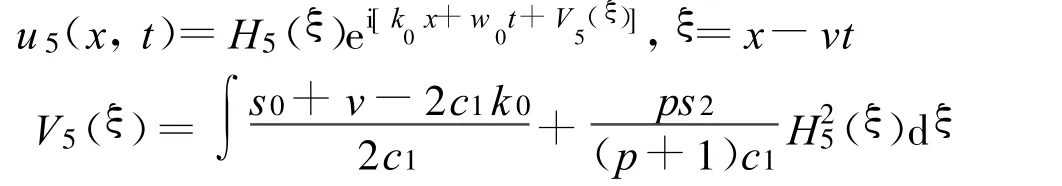
其中

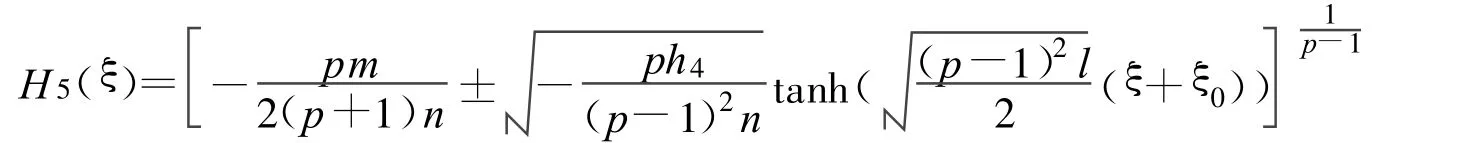
定理4 假设

如果 l＞0,p＜4,方程(2)有一扭孤立波解：

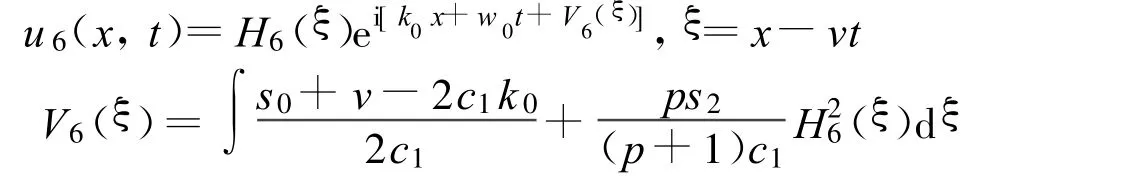
其中

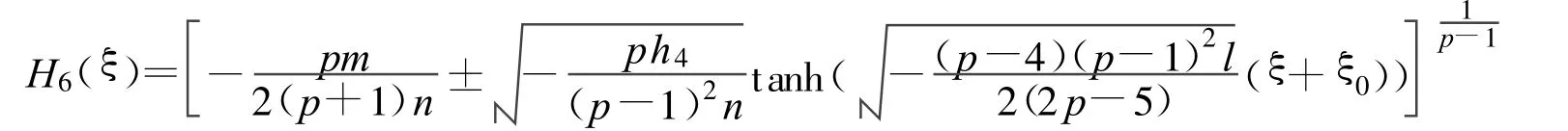
情形3(Jacobi椭圆函数解)

定理5 假设

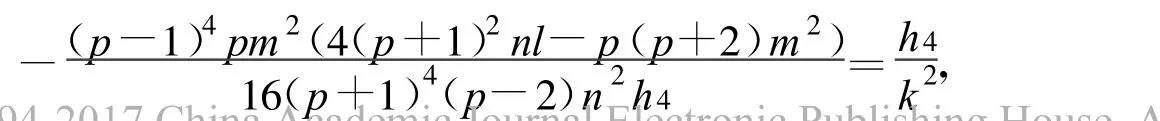
方程(2)可以得到两个Jacobi椭圆函数解：

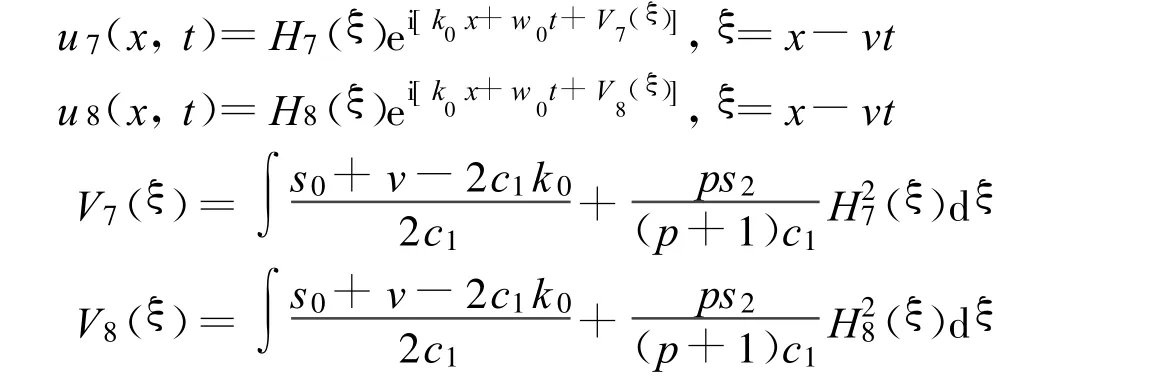
其中：

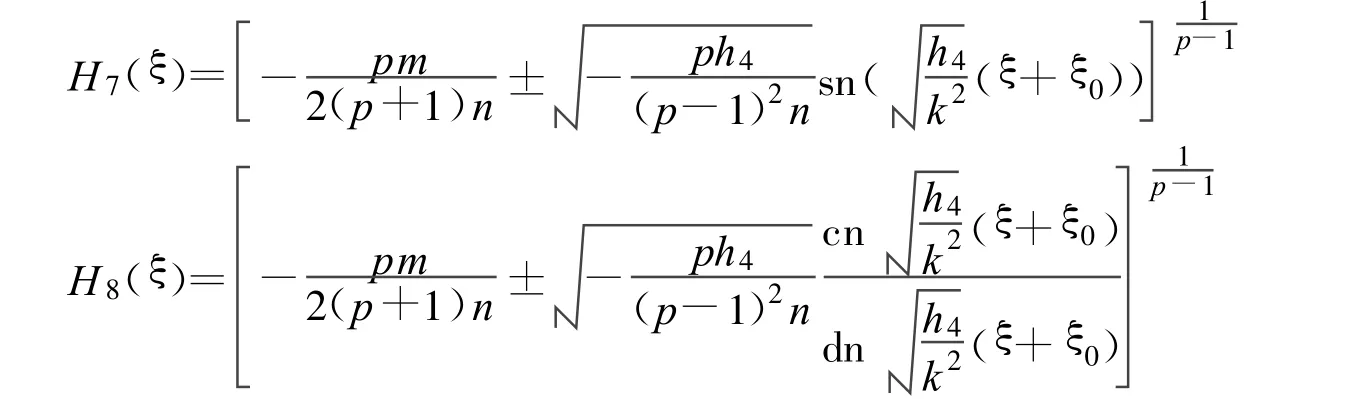
定理6 假设

方程(2)可以得到一个Jacobi椭圆函数解：

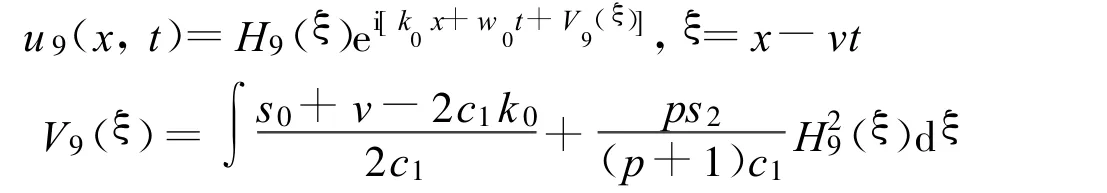
其中：

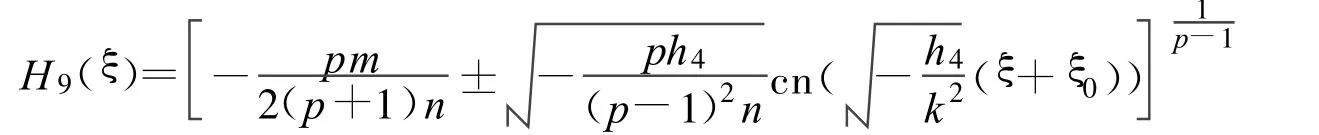
定理7 假设

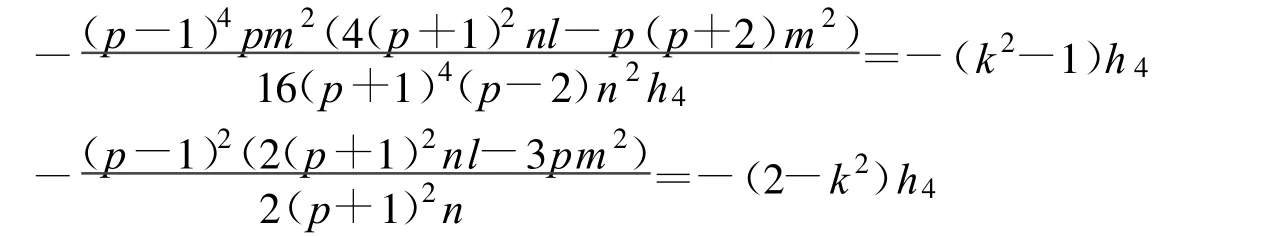
方程(2)可以得到一个Jacobi椭圆函数解：

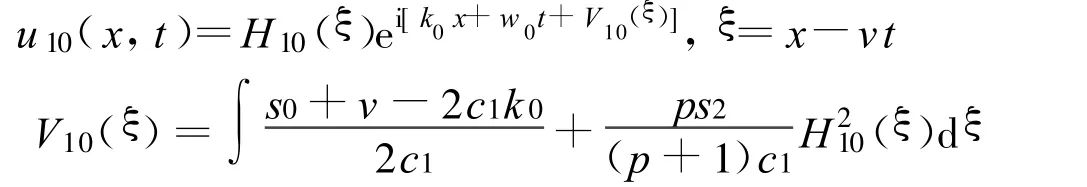
其中：

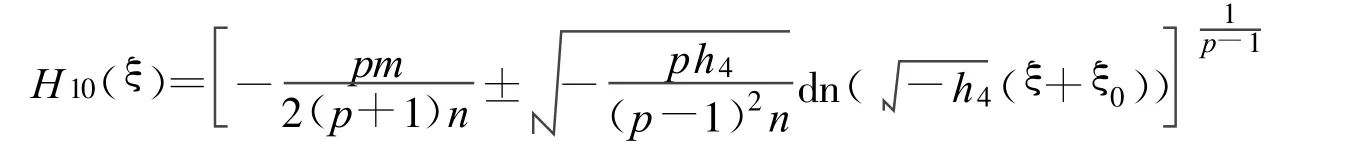
定理8 假设

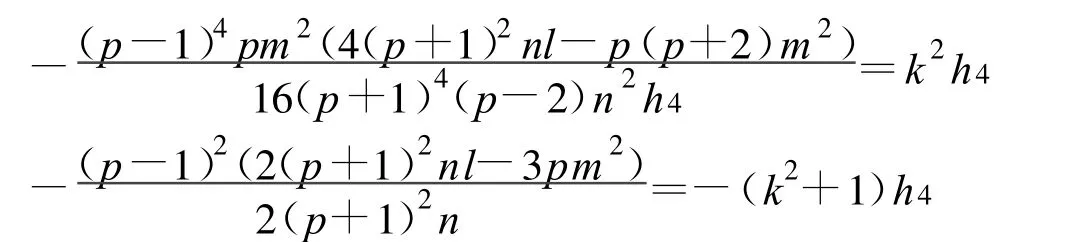
方程(2)可以得到一个Jacobi椭圆函数解：

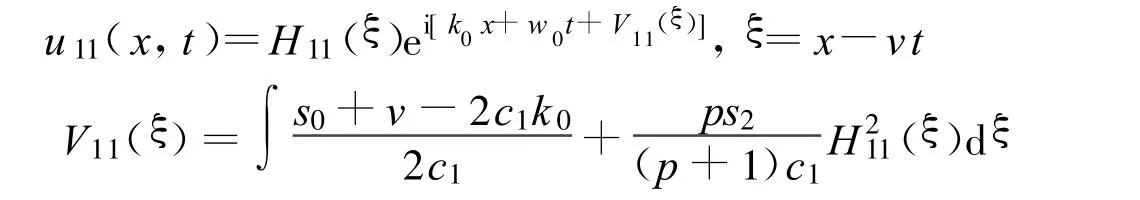
其中：

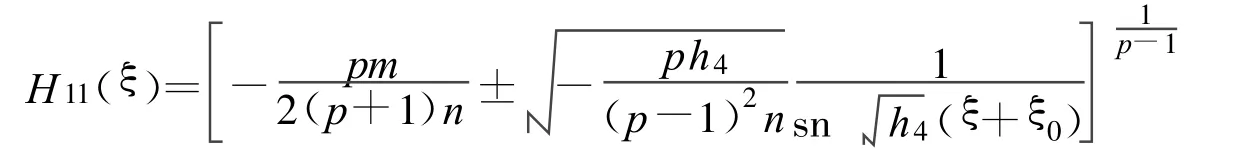
定理9 假设

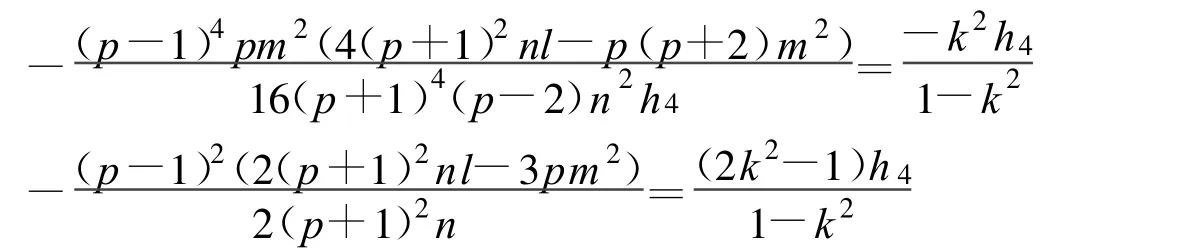
方程(2)可以得到一个Jacobi椭圆函数解：

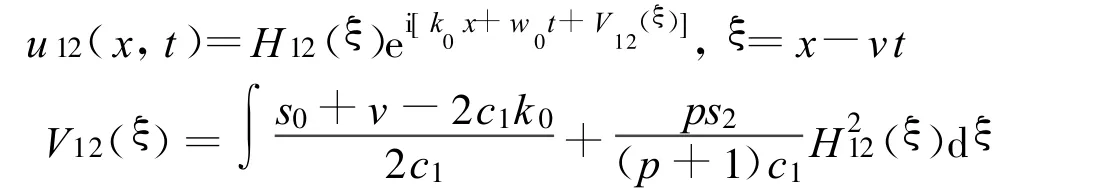
其中

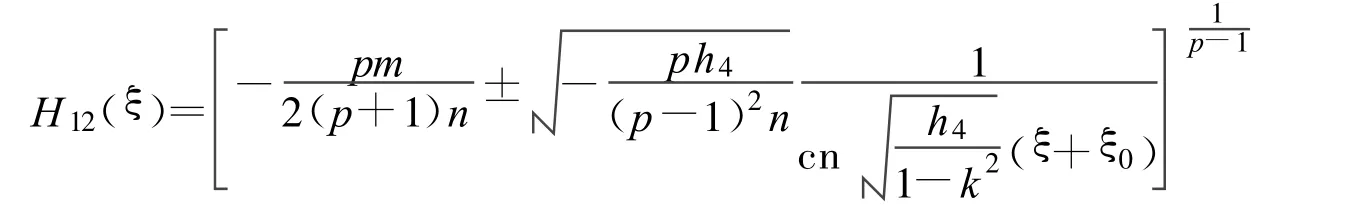
定理10 假设

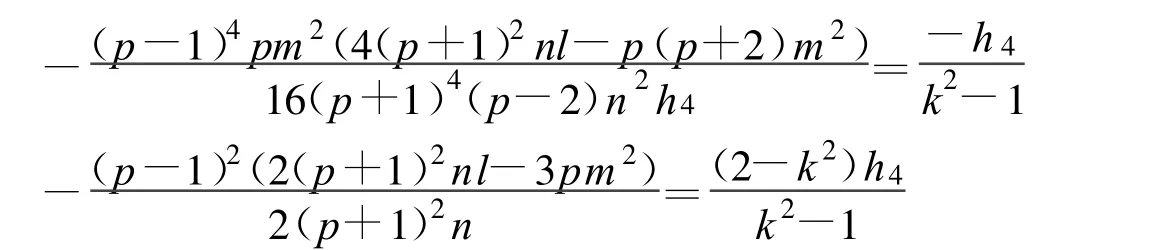
方程(2)可以得到一个Jacobi椭圆函数解：

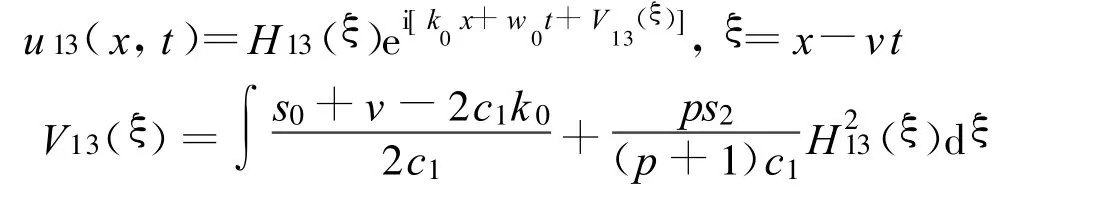
其中：

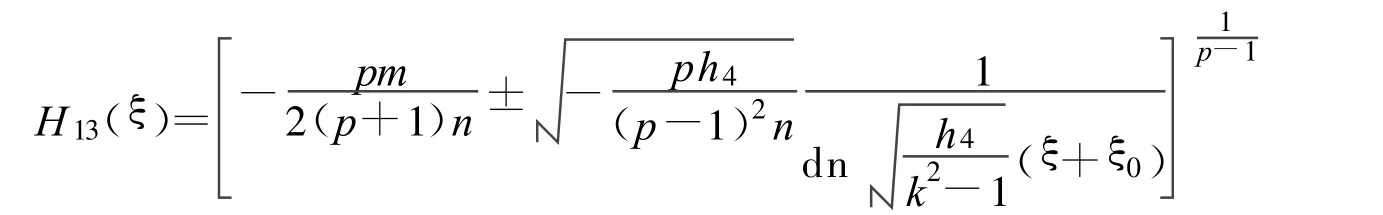
定理11 假设

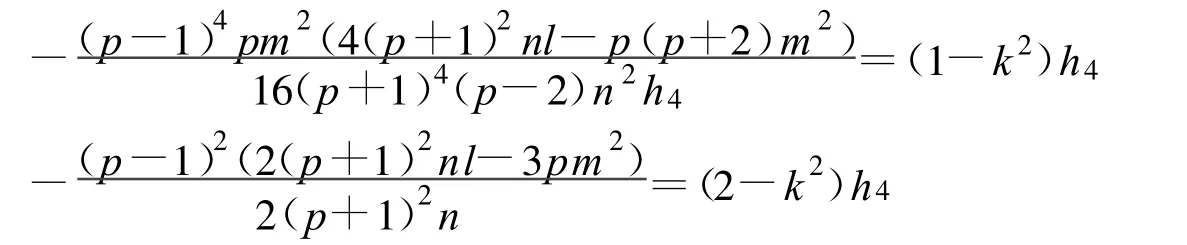
方程(2)可以得到一个Jacobi椭圆函数解：

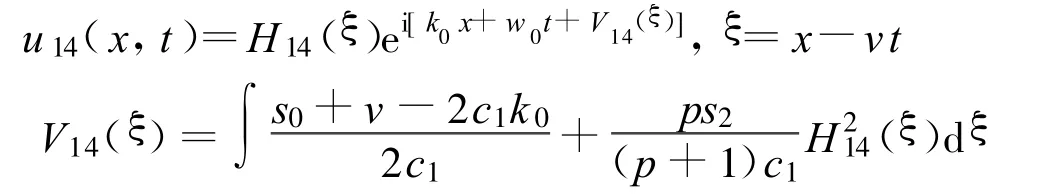
其中：

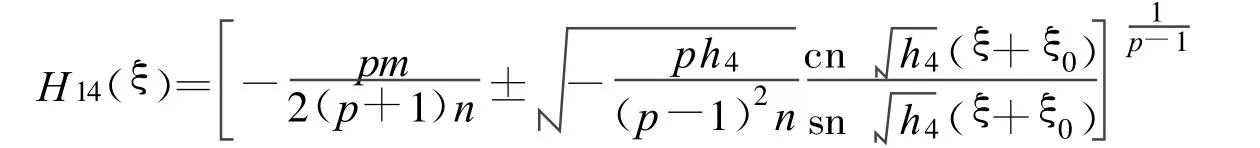
定理12 假设

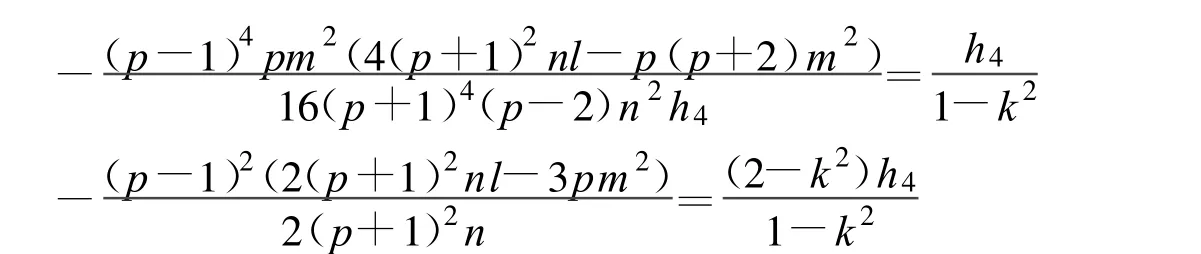
方程(2)可以得到一个Jacobi椭圆函数解：

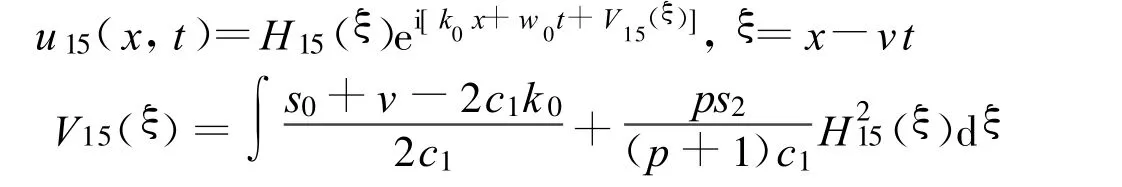
其中：

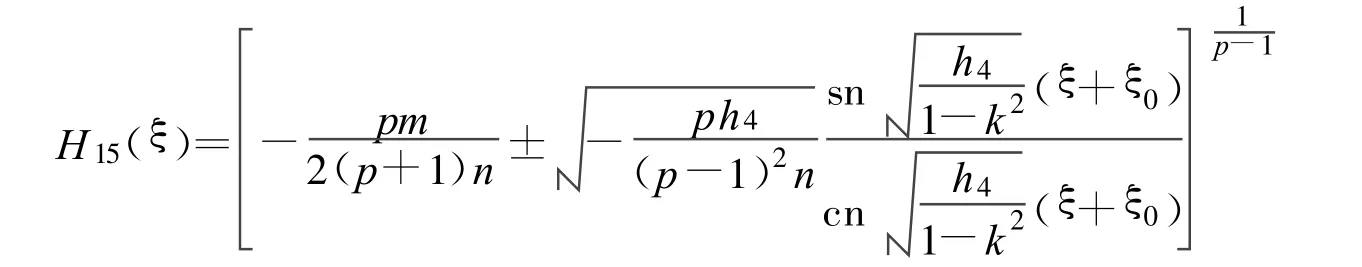
定理13 假设

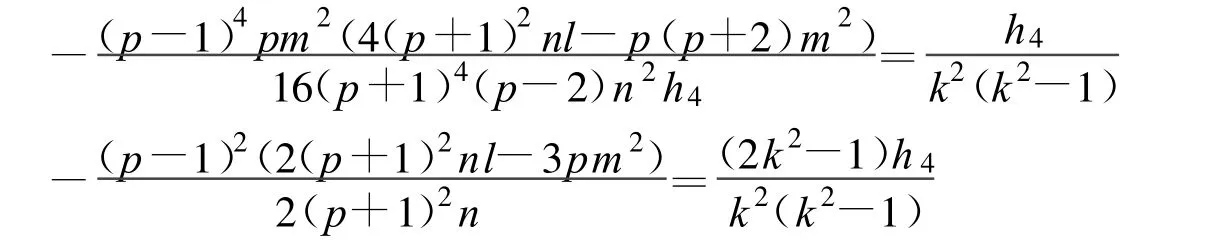
方程(2)可以得到一个Jacobi椭圆函数解：

其中：

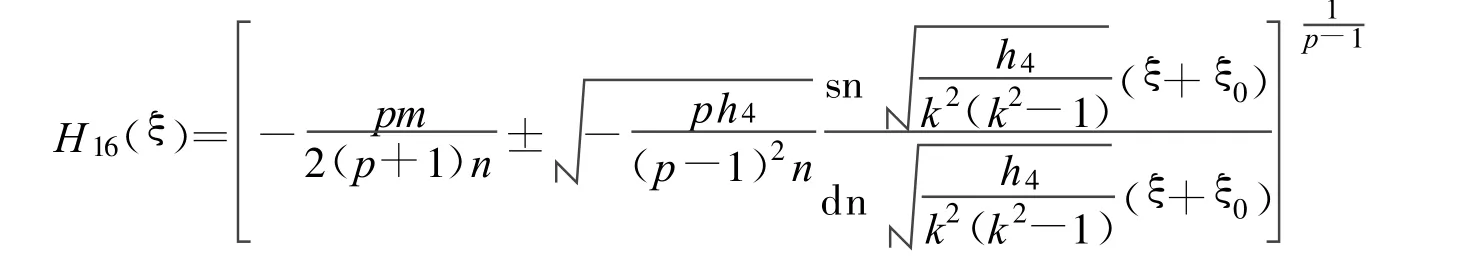
定理14 假设：

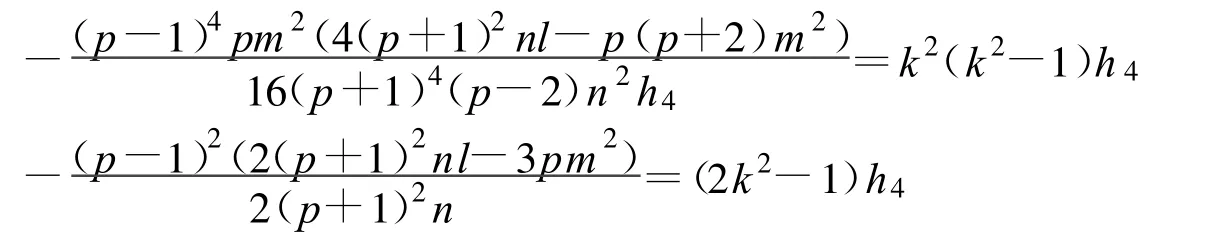
方程(2)可以得到一个Jacobi椭圆函数解：

其中：

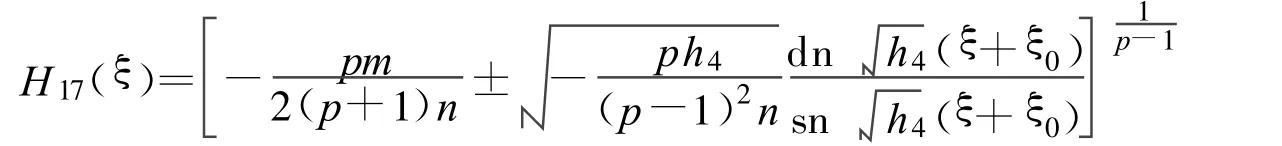
定理15 假设：

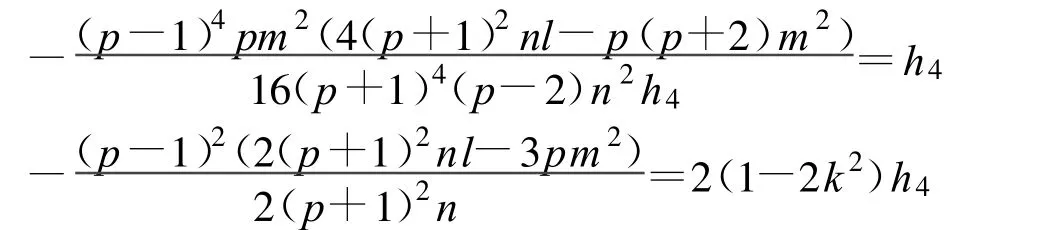
方程(2)可以得到4个Jacobi椭圆函数解：

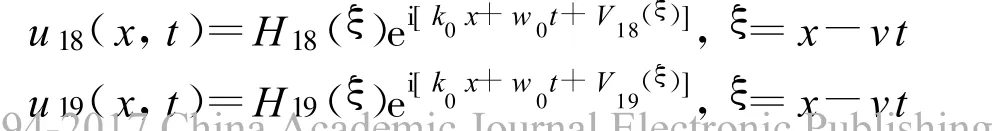
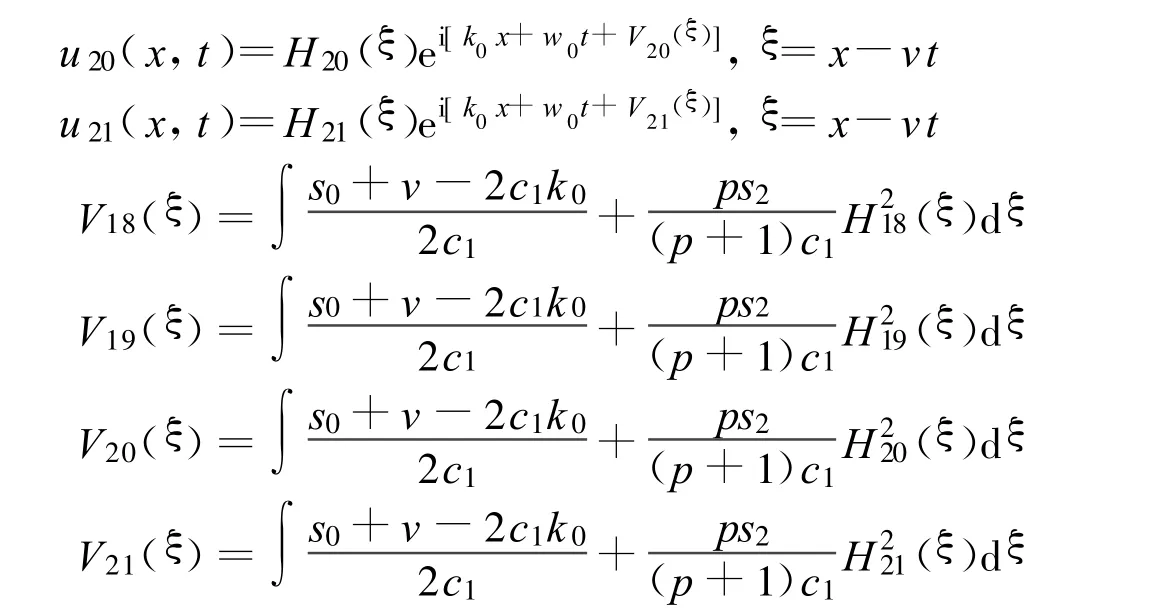
其中

定理16 假设

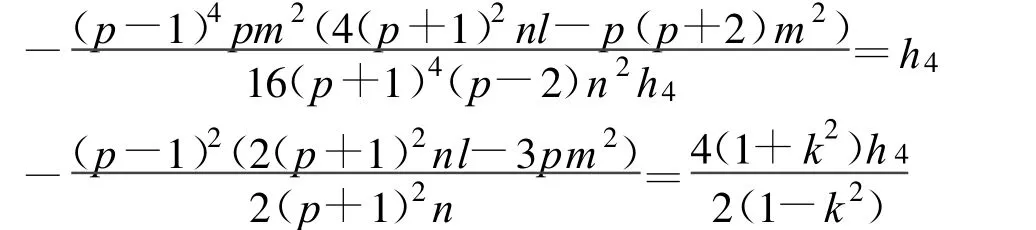
方程(2)可以得到1个Jacobi椭圆函数解：

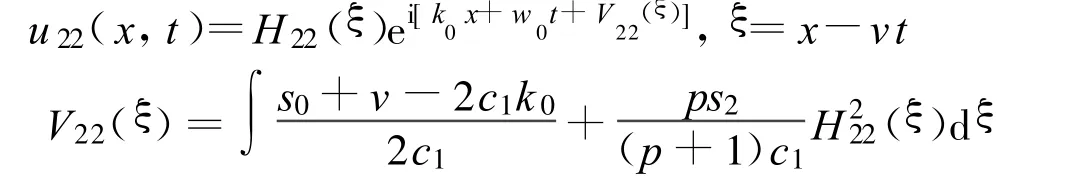
其中：

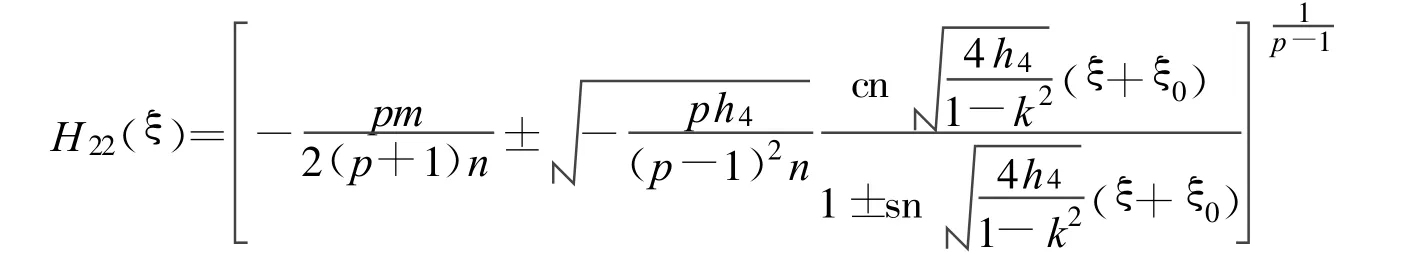
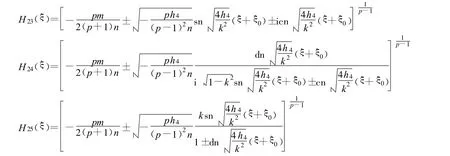
定理17 假设

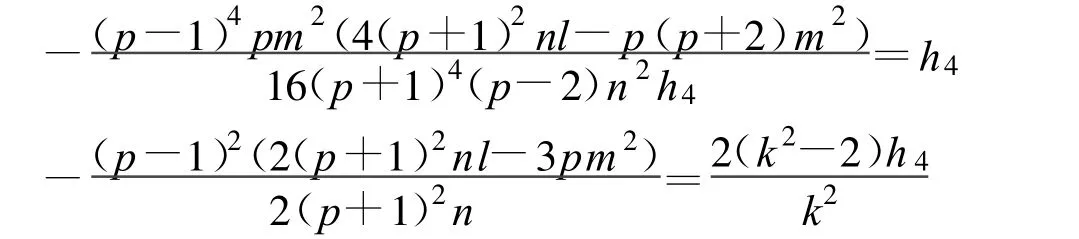
方程(2)可以得到3个Jacobi椭圆函数解：

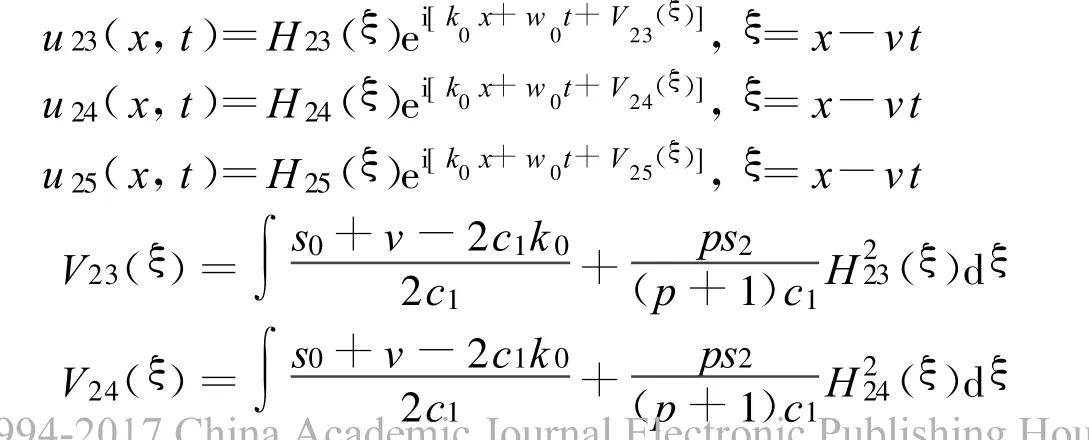
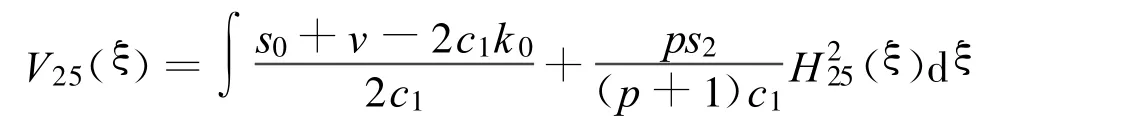
其中

定理18 假设

方程(2)可以得到1个Jacobi椭圆函数解：

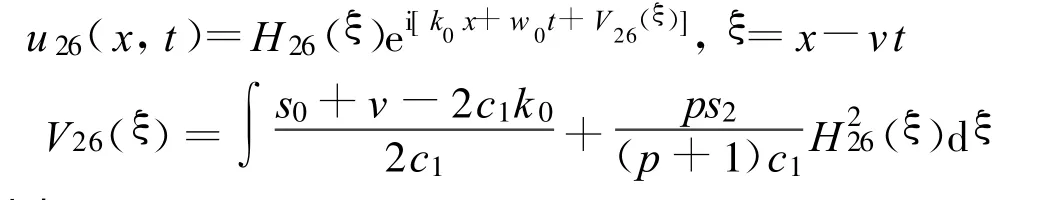
其中

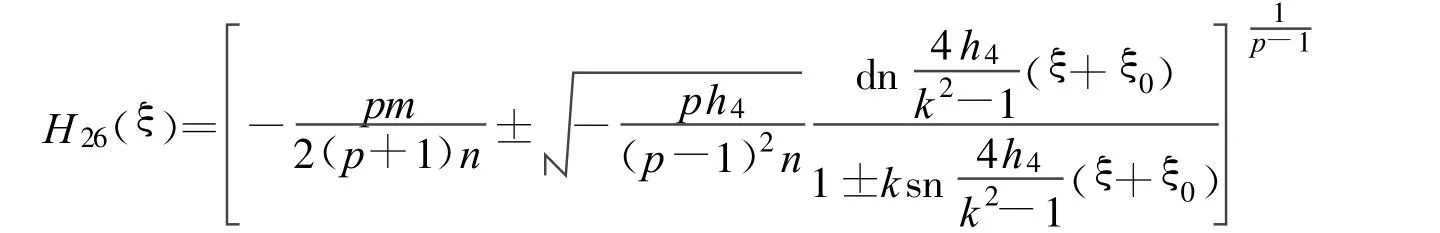
定理19 假设

方程(2)可以得到1个Jacobi椭圆函数解：

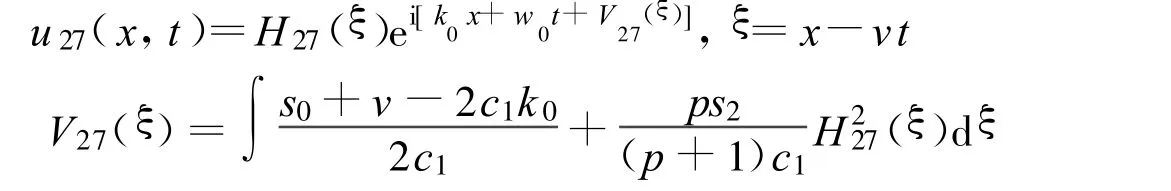
其中

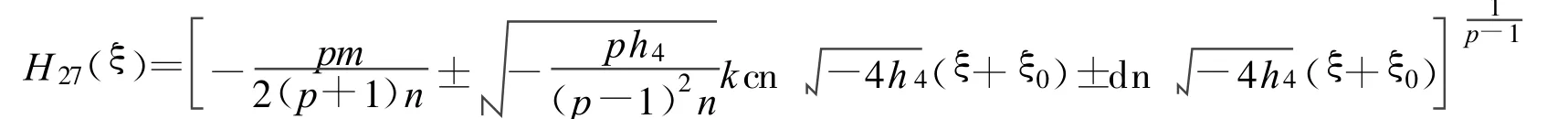
定理20 假设

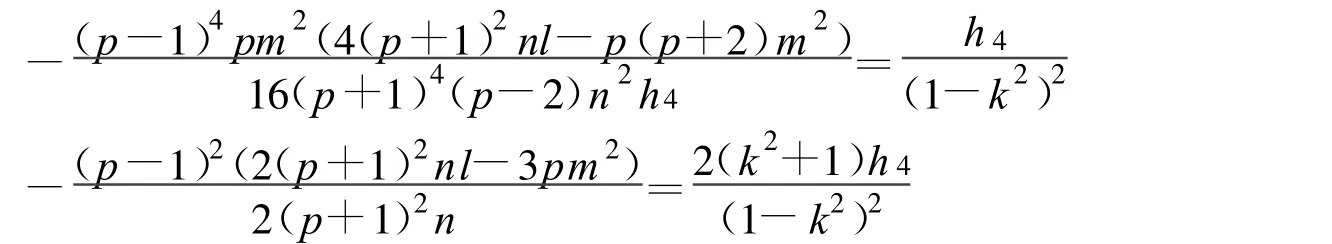
方程(2)可以得到1个Jacobi椭圆函数解：

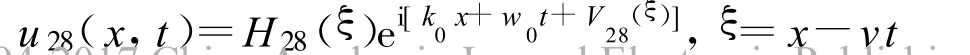
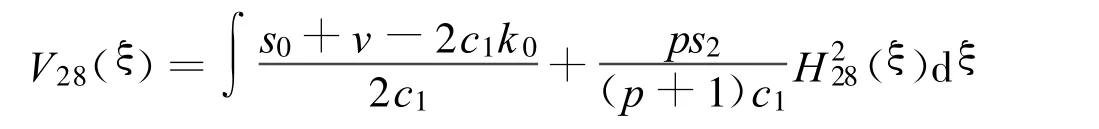
其中

定理21 假设

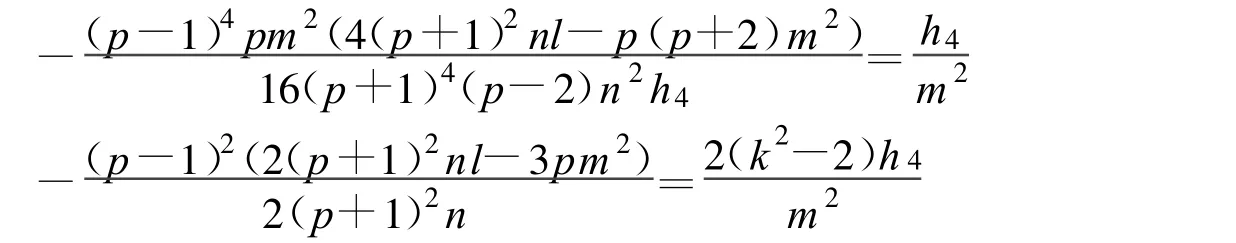
方程(2)可以得到1个Jacobi椭圆函数解：

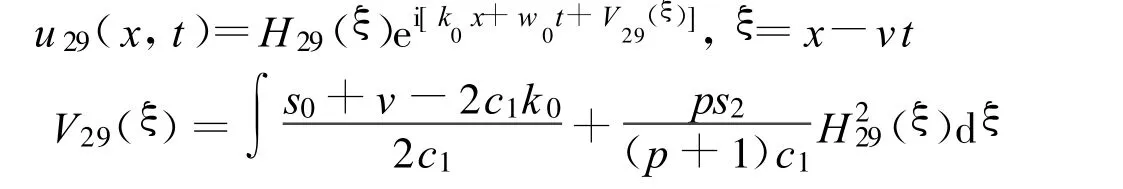
其中

3 结束语

利用辅助方程来求解具有任意阶的非线性薛定谔方程(2),给出了一些新的孤波解、三角函数解、扭孤立波解、Jacobi椭圆函数解。可以利用这些解来解释一些非线性物理现象。

[1]W P Hong.Dynamics of solitary-waves in the higher order Korteweg-de Vries equation type：I[J].Zeitschrift fur Naturforschung,2005,60(11/12)：757-767.

[2]J Li,W Rui,Y Long.Travelling wave solutions for higher-order wave equations of KdV type：III[J].Mathematical Biosciences and Engineering,2006,3(1)：125-135.

[3]Y Long,J Li,W Rui.Traveling wave solutions for a second order wave equation of KdV type[J].Applied Mathematics and Mechanics,2007,28(11)：1455-1465.

[4]V Marinakis.New solutions of a higher order wave equation of the KdV type[J].Journal of Nonlinear Mathematical Physics,2007,14(4)：519-525.

[5]V Marinakis.New solitary wave solutions in higher-order wave equations of the Korteweg-de Vries type[J].Zeitschrift fur Naturforschung,2007,62(5/6)：227-230.

[6]A blowitz MJ,Clarkson PA.solution nonlinearn evolution equations and inverse scattering[M].Cambridge：Cambridge University press,1991.

[7]Wadati M.WAVE Propagation in Nonlinear Lattice[J].Phys.Soc Jan 1975,38：673.

[8]Wadati M,Sanuki H,Konno K.A Generalization of Inverse Scattering Method[J].Prog Theor Phys.,1975,53：419.

[9]Matveev VB,Salle MA.Darboux transformation and solitons[M].Berlin：Springer,1991.

[10]Gu CH,Hu HS,Zhou ZX.Darboux transformation in solition thory and its geometric applications[M].Shang-hai：Shanghai Sci Tech Publ,1999.

[11]Rogers C,Schief WK B.acklund and Darboux transformation,geometry and modern application in soliton[M].Cambridge：Cambridge University press,2002.

[12]Hirota R.Direct methods in soliton theroy.In：Bullough PK,Caudrey PJ,editors[M].Solitons.Springer,1980.

[13]Olver PJ.Applications of Lie groups to di.erential equations[M].New York：springer;1993.

[14]Ding-jiang Huang,De-sheng Li,Hong-qing Zhang.Explicit and exact travelling wavesolution for the generalized derivative schrodinger equation,Chaos,Solution and Fractals[J].2007,31：586-593.