张婷婷

(陕西师范大学 数学与信息科学学院， 陕西 西安 710062)

0 引 言

Sturm-Liouville理论经过一个半世纪的发展日趋完善，其应用已涉足于数学物理、工程技术、地球物理和气象物理等各类应用及理论学科.一端固定的非均匀的张紧弦的自由振动问题可描述为Sturm-Liouville弦方程问题L(ρ，h) (简称SL弦问题).

y″(x)+λρ2(x)y(x)=0,x∈[0,1]

(1)

y(0)=0,y′(1)-hy(1)=0

(2)

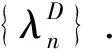
本文的目的是将文献[6]的结论推广到弦方程.我们将证明当密度函数是分段常值的正函数时，一组谱不仅在对分段区间重新排列的意义下可确定密度函数，而且能同时确定边界条件.进一步地，如果问题同时具有对称性，则半组谱即可确定密度函数和边界条件.

1 预备知识

如文献[6],我们还需做以下假设：

(C2)若记μn=ρn/ρn+1(n=0,…,N-2) ,则μn≠1.

设φ(x,λ) 是方程(1)满足初始条件y(0)=0,y′(0)=1的基本解，则由ρ(x)的结果知，在区间(xn,xn+1) 内φ(x,λ)可表示为：

φn(x,λ)=Cncos(ρnω[x-xn])+(Dn/ω)sin(ρnω[x-xn])

(3)

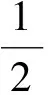
由φ(x,λ)和φ′(x,λ)在x∈[0,1]上的连续性，可计算出Cn和Dn与Cn+1和Dn+1之间的线性映射关系

(4)

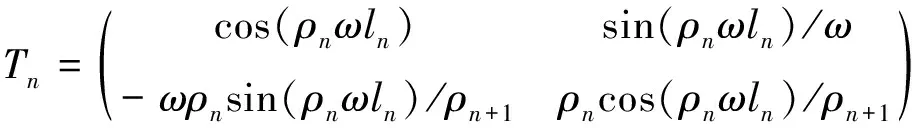
(5)

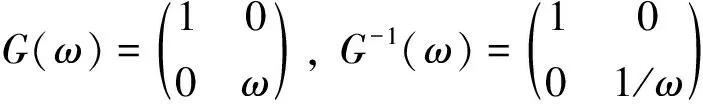
(6)

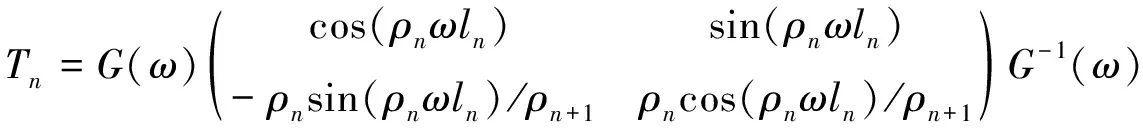
(7)

为了由C0和D0得到Cn和Dn，我们需要计算Tn…T0.

引理1.1

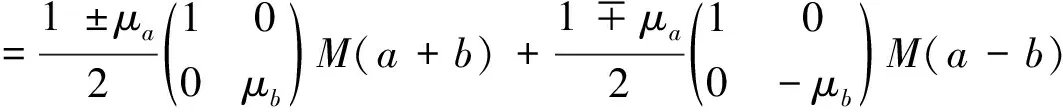
(8)

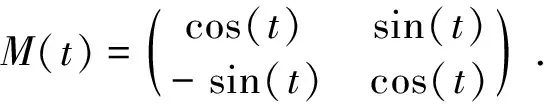
该引理可以由三角恒等式直接证明(也可参考文献[6]的引理2.1).

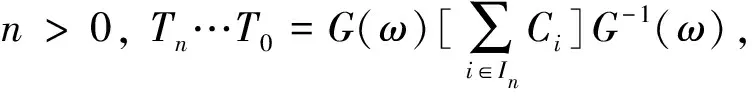
(9)

该引理可由数学归纳法结合引理1.1证得(也可参考文献[6]的引理2.2).

引理1.3Sturm-Liouville弦方程问题L(ρ,h) 的特征函数F0(λ)可表示为

(10)

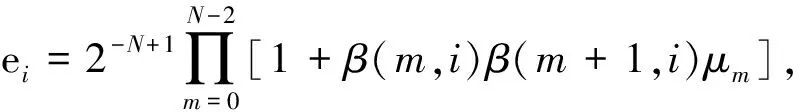
证明由初始条件φ(0,λ)=0,φ′(0,λ)=1知C0=0,D0=1/ρ0.由(3)和(4)可得在最后一个区间(xN-1,xN)内的解可表示为

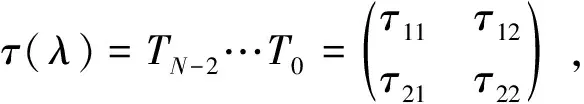
φN-1=τ12/ρ0·cos(ρN-1ω[x-xN-1])+τ22/ρ0·sin(ρN-1ω[x-xN-1])/ω,

从而可得

于是

记ρN=1,μN-1=ρN-1,则有

(11)

由边界条件(2)可知，L(ρ,h)的特征函数为

再由引理1.2可得

(12)

将(6)和(9)代入后整理即得(10)，得证.

引理1.4存在非零常数c，使得

(13)

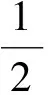
2 定理及证明

为了文章中叙述的方便，我们作如下定义：

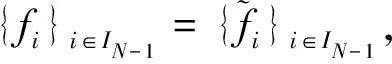
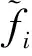
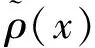
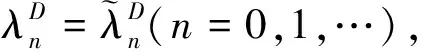
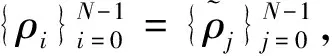
(14)

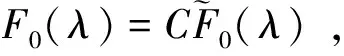
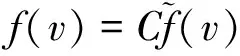
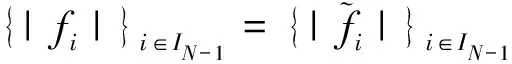
(15)

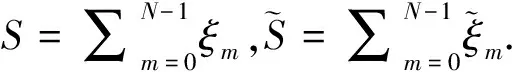
(16)

再由{ξm}的递增假设可知

S0=-ξ0+ξ1+…+ξn-1=S-2ξ0

(17)

(18)

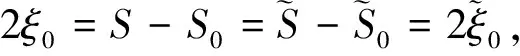
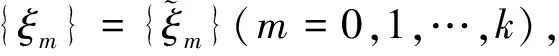
对于ξ0…ξN-1的每一个排列，将产生不同的∑β(m,i)ξm和ei(i∈IN-1),选取i使得β(0,i)=…=β(k,i)=1,β(k+1,i)=…=β(N-1,i)=-1，有

再选取另外一个i使得β(0,i)=…=β(N-1,i)=1，有

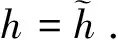
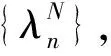
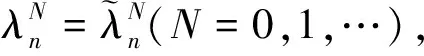
若密度函数ρ(x)是[0,1]上的偶函数，即ρ(x)=ρ(1-x)，且边界条件为：

y′(0)-hy(0)=0,y′(1)+hy(1)=0

(20)

则有如下结论成立：

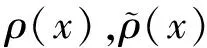
证明 令t=1-x,z(t)=Ψ(1-t)，则有Ψ(x)=Ψ(1-t), 故z′(t)=-Ψ′(t),z″(t)=Ψ″(x)，所以有

z″(t)+λρ2(1-t)z(t)=0

(21)

再由ρ(t)=ρ(1-t)，方程(21)变为

z″(t)+λρ2(t)z(t)=0

(22)

由(20)可得

z′(0)-hz(0)=0,z′(1)+hz(1)=0

(23)

所以Ψ(1-x)=CΨ(x).由Ψ(0)=Ψ(1-1)=CΨ(1),Ψ(1)=Ψ(1-0)=CΨ(0) 得C2=1.

根据特征函数的振动性可知：对应于λ2n+1的特征函数Ψ(x,λ2n+1)有偶数个零点，故此时C=1,所以有Ψ(1-x)=Ψ(x)，即Ψ(x)是偶函数；对应于λ2n的特征函数Ψ(x,λ2n)有奇数个零点，故此时C=-1,所以有Ψ(1-x)=-Ψ(x)，即Ψ(x)是奇函数.得证.(可参考文献[8]).

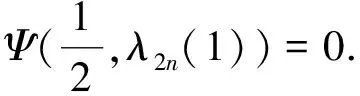
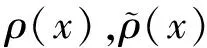
参考文献

[1] Ambagumyan VA. Uber eine frage der eigenwertthewrie[J].Z.Phys.,1929,53:690-695.

[2] Borg G..Eine umkehrung der sturm-liouvilleschen eigenwertaufgabe[J].Acta.Math.,1946,78:1-96.

[3] Hochstadt H, Lieberman B.An inverse sturm-liouville problem with mixed given data[J].Siam J. Appl.Math.,1978,34:676-680.

[4] Hald O.Inverse eigenvalue problems[J].Comm.Pure. Appl.Math.,1984,37:539-577.

[5] Gesztesy F,Simon B.Inverse spectral analysis with partial information on the potential(ii) the case of discrete spectrum[J].Trans.Amer.Math.Soc.,2000,352:2 765-2 787.

[6] Robert Carlson.An inverse spectral problem for sturm-liouville operators with discontinuous coefficients[J].Proceedings of the American Mathematical Society,1994,9:475-484.

[7] Chao L S. On some inverse spectral problems related to the ambarzumyan problem and the dual string of the string equation[J].Inverse Problems,2007,23:2 417-2 346.

[8] Markushevich A I.Theory of functions of a complex variable(2ed.)[M].Chelsea,New York,1985.

[9] Gladwell G.Inverse problems in vibration[M].Second edition ,kluwer academic pubishers,2004.