郑芳英， 张连生

(1.上海大学理学院，上海200444;2.浙江理工大学数学科学系，杭州310018)

本研究考虑如下的约束优化问题：

式中，f，hj，gl∈C1，C1表示连续可微函数集，E，I分别表示等式约束函数以及不等式约束函数的指标集，并且E={1，2，…，m}，I={1，2，…，k}，“L-min”表示所求的问题为局部极小问题.

到目前为止，有很多方法可用于求解一般约束优化问题(P)，如序列二次规划(sequential quadratic programming，SQP)方法、SQP信赖域法、虑子法［1］以及罚函数方法等，其中罚函数方法［2-8］是求解约束优化问题的重要途径之一.罚函数方法是通过罚函数将约束优化问题转化为无约束优化问题或仅含简单约束的优化问题，从而可以利用无约束优化问题的求解算法来求解约束优化问题.传统的罚函数，要么是简单精确，但非光滑的，如l1精确罚函数［9］;要么是简单光滑，但非精确的，如二次罚函数［10］;要么是精确光滑，但非简单的，如增广拉格朗日罚函数［11-12］.这里的“简单”是指罚函数的表达式中仅含目标函数和约束函数，而不含其梯度信息.

通过增加一个变量，Huyer等［13］针对含箱子约束的等式约束优化问题，给出了一个新的简单精确罚函数fσ(x，ε)，并且得到了如下结论：当σ＞0充分大及 ε＞0时，罚问题(Pσ)不存在 KKT(Karush-Kuhn-Tucher)点.特别地，对于充分大的σ＞0，具有有限目标函数值的罚问题(Pσ)的每个局部极小点(xσ，εσ)，都具有(xσ，0)形式，且xσ为原问题(P)的一个局部极小点.但在实际计算中，当ε＞0时，仅能计算罚问题的KKT点.另一方面，文献［13］中给出的罚函数在ε=0处是不可微的，这在实际计算中会受到很多的限制.

受到文献［13］的启发，本研究针对一般约束优化问题(1)，给出了一个新的简单精确光滑罚函数.在较弱的约束品性的假设下，首先证明所给出的罚函数在ε=0处是连续可微的.对充分大的罚参数σ＞0，具有有限目标函数值的罚问题(Pσ)的每个局部极小点(xσ，εσ)，都具有(xσ，0)形式，且xσ为原问题(P)的一个局部极小点.针对新的罚函数，本研究给出了两个数值算例及计算结果，并提出了一些未来需要解决的问题.

1 一个新的简单精确光滑罚函数

对问题(1)，定义如下集合：

式中，wj，wl∈(0，1)，j∈E，l∈I.L(P)：问题(P)的局部极小点构成的集合.显然，S=Sε0，因此，下面的问题与问题(1)等价：

相应地，罚函数fσ(x，ε)及罚问题(Pσ)如下：

下面讨论所给出的罚函数fσ(x，ε)的光滑性和精确性.

定理1 当参数α，β，γ，δ以及N满足一定条件时，罚函数fσ(x，ε)在{(x，ε)∈Rn+1：ε=0，x∈S或者ε≠0，0＜1-cε-NδΔ(x，ε)≤1}上连续可微.

证明 记Δ(x，ε)fσ(x，ε)为fσ(x，ε)的梯度，则对任意的(x，ε)∈Rn+1，有

若ε=0，x∈S，则

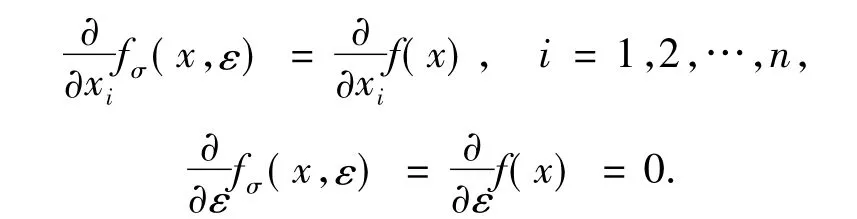
若ε≠0，0＜1-cε-NδΔ(x，ε)≤1，则

当ε≠0，0＜1-cε-NδΔ(x，ε)＜1，ε→ε*=0时，有Δ(x，ε)=O(εNδ)，从而有

整理得

当x→x*∈S，ε→0时，有

事实上，满足式(5)的α，β，γ，δ以及N是存在的，例如取N=2，γ＞1，δ＞α，β＞1时，式(5)成立.因此，函数fσ(x，ε)在{(x，ε)∈Rn+1：ε=0，x∈S或者ε≠0，0＜1-cε-NδΔ(x，ε)≤1}上连续可微.

下面讨论罚函数fσ(x，ε)的精确性，即在一定条件下，证明存在σ0＞0，当σ≥σ0时，罚函数的局部极小点具有(xσ，εσ)形式.这里εσ=0，且xσ为原问题的一个局部极小点.

引理1 如果(x(k)，εk)∈L(Pσk)，其函数值fσk(x(k)，εk)为有限值，εk≠0，且参数α，β，γ，δ，N满足式(5)，则(x(k)，εk)∉Sεk.

显然，当εk≠0时，σkβ＞0，从而式(6)矛盾，故(x(k)，εk)∉Sεk.

证明 由题设条件知

由式(8)可得

由式(7)可得

假设I+(x*，ε*)I0(x*，ε*)≠Ø，其I0(x*，ε*)={l：gl(x*)=ωl，l∈I}，则至少存在 l0∈I+(x*，ε*)I0(x*，ε*)，满足gl0(x*)-ωl0＞0.根据题设，M-F约束品性在x*处成立，因此，存在p∈Rn，使得下式成立：

由式(12)，有

定理3 如果定理2的条件成立，并且参数α，β，γ，δ，N满足相应的条件，则存在k0＞0，使得当k≥k0时，有εk=0，xk∈L(P).

即

另一方面，根据 fσ(x，ε)的定义以及函数值fσk(x(k)，0)为有限值，可知x(k)∈S.因为(x(k)，0)∈L(Pσk)，即存在(x(k)，0)的一个邻域 o((x(k)，0)，ρk)，ρk＞0，对任意的点(x，0)∈o((x(k)，0)，ρk)，x∈S，f(x(k))=fσk(x(k)，0)≤fσk(x，0)=f(x)都成立，即x(k)∈L(P)，所以定理成立.证毕.

2 数值算例

基于软件Matlab 7.0的环境，利用Matlab的库函数fmincon来求解罚问题(Pσ)，从而验证所给出的罚函数对于求解约束优化问题是有效的.表1和表2分别为两个算例的数值结果，其中分别列出了罚参数σk，最后得到的最优解x(k)，εk以及相应的目标函数值f(x(k)).

(1)问题1.

该问题为一个二次规划问题，存在18个局部极小值点.在该算例中，我们取α=β=2，δ=4，γ=10，ω= 0.005，N=4，选取初始点为x(0)=(0.000 0，0.000 0，0.000 0，0.000 0，0.000 0，0.000 0)，ε0=2，从而得到其中一个局部极小点为x*=(0.000 0，0.000 0，5.000 0，0.000 0，5.000 0，0.000 0)，极小值为f(x*)=-168.000 0，具体计算结果如表1所示.

(2)问题2.在该算例中，我们取α=2，β=4，δ=2，γ=2，N=4，ω=0.05，选取初始点 x(0)=(0.000 0，0.000 0，0.000 0)，ε0=2，从而得到问题2的极小点为x*= (1.000 0，-1.000 0，1.000 0)，对应的极小值为f(x*)=-7.000 0，具体计算结果如表2所示.

表1 问题1的数值结果Table 1 Numerical results of Problem 1

表2 问题2的数值结果Table 2 Numerical results of Problem 2

3 结束语

本研究得到了求解约束优化问题的一个新的方法——简单光滑精确罚函数法.对于约束优化问题是否存在具有二次可微的简单精确罚函数，还需要进一步的研究和探讨.

［1］ FLETCHERR，LEYFFERS，TOINTP L.On the global convergence of a filter-SQP algorithm［J］.SIAM Journal on Optimization，2002，13(1)：44-59.

［2］ PILLOG D I.Exact penalty methods［M］.Netherlands：Kluwer Academic Publisher，1994：209-253.

［3］ PILLOG D I，GRIPPOL.Exact penalty functions in constrained optimization［J］.SIAM Journal on Control and Optimization，1989，27(6)：1333-1360.

［4］ PILLOG D I，GRIPPOL.An exact penalty function method with global convergence properties for nonlinear programming problems［J］.Mathematical Programming，1986，36：1-18.

［5］ PILLOG D I，LUCIDIS.An augmented Lagrangian function with improved exactness properties［J］.SIAM Journal on Optimization，2002，12(2)：376-406.

［6］ FLETCHERR.An exact penalty function for nonlinear programming with inequalities［J］. Mathematical Programming，1973，5：129-150.

［7］ FLETCHERR.Practical methods of optimization(2)：constrained optimization［M］.Wiley：John Wiley＆Sons，1981.

［8］ HANS P，MAGASARIANO L.Exact penalty functions in nonlinear programming［J］.Mathematical Programming，1979，17：251-269.

［9］ ZANGWILLW I.Nonlinear programming via penalty functions［J］.Management Science，1967，13：344-358.

［10］ FIACCOA V，MCCORMICKP.Nonlinear programming：sequential unconstrained minimization techniques［M］.Wiley：John Wiley＆Sons，1968.

［11］ HESTENESM R.Multiplier and gradient methods［J］.Journal of Optimization Theory and Applications，1969，4：303-320.

［12］ POWELLM J D.On the convergence of the variable metric algorithm ［J］.JournaloftheInstituteof Mathematics and Its Applications，1971，7：21-36.

［13］ HUYERW，NEUMAIERA.A new exact penalty function［J］.SIAM Journal on Optimization，2003，3(4)：1141-1158.