刘万增，陈 军，闫超德，赵仁亮，赵 勇，孙文彬

1.国家基础地理信息中心，北京100830；2.中国矿业大学（北京）地球科学与测绘工程学院，北京100083；3.郑州大学地理信息工程系，河南郑州450001

1 引 言

邻近关系是平面离散点集的重要拓扑特性。在GIS中，点是构成空间目标的最简单元素，平面离散点集的Voronoi图确定了其间的邻近关系，构成离散点间的拓扑结构［1－2］。GIS中点集邻近关系的建立、维护与重构对于GIS中数据综合［3－6］、位置服务、数据库更新以及人工智能领域等具有重要意义。一般认为，随着某一点的移动，平面离散点集的Voronoi图局部会发生变化，从而引起平面离散点集局部拓扑结构的改变［7－8］。其实，在点目标周围存在这样一个区域，目标在其内移动，不会引起其与周围邻近点的拓扑结构的变化，称该区域为拓扑邻近稳定区域。拓扑邻近稳定区域的确定是维护目标间的拓扑结构的基础。目前关于这一问题的研究较少，文献［9—11］从不同角度研究点目标移动时，其与周围点目标邻近关系的变化，并给出定性描述，但关于目标拓扑邻近稳定区域的定义及其定量计算或描述的研究目前尚未见到。本文对这一问题进行研究，证明点的拓扑邻近稳定区域必须满足的两个条件，并给出其定量计算模型。

2 拓扑邻近稳定区域的确定

如图1为平面上的离散点集｛P0，P1，P2，…，P5｝的Voronoi图及其对偶Delaunay三角网。如果平面上两点连线为Delaunay三角网的一条边，则称该两点一阶邻近（即如果Line（Pi，Pj）∈DT，则（Pi，Pj）＝true，其中，DT为Delaunay triangle的边集合）。将图1中点P0定义为活动点，依次连接其一阶邻近点得到一个多边形P1P2P3P4P5，称之为移动点P0的一阶邻近多边形，用ADJpolygon（P0）表示。图1中P0点在深色区域内移动，其与点P1、P2、P3、P4、P5的一阶邻近关系不会改变，同时，没有新的一阶邻近点产生，即P0点与点P1、P2、P3、P4、P5组成的一阶邻近多边形ADJpolygon（P0）不会发生变化。分析认为，拓扑邻近稳定区域也就是在保证一阶邻近多边形不变的情况下活动点P0的移动区域。以下首先证明点的拓扑邻近稳定区域必须满足的两个条件，以此为基础研究活动点拓扑邻近稳定区域确定方法。

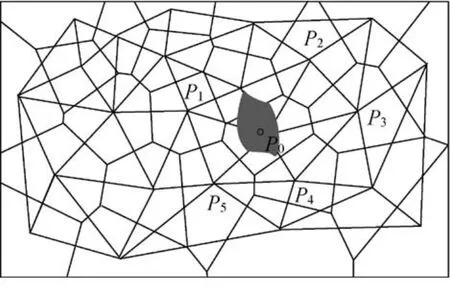
图1 平面离散点集及其邻近关系Fig.1 The neighboring relations between the plane discrete points

2.1 不改变原一阶邻近点的活动点移动区域

如图1，在活动点P0移动过程中，要保持其一阶邻近多边形不变，首先必须满足其与点P1、P2、P3、P4、P5的一阶邻近关系不会改变。反过来，如果要满足点P0与点P1、P2、P3、P4、P5一阶邻近关系不变，那么点P0的允许移动区域需要确定。平面上任意3个非共线点可以确定一个外接圆，根据Delaunay三角网的空圆规则可以判断活动点P0与任意3个非共线点的邻近关系［12］。以上的例子中，若点P0与点P1、P2、P3、P4、P5一阶邻近关系不变，则P0与点P1、P2、P3、P4、P5中任意相邻3点一阶邻近关系不变；反过来，若点P0同时与点P1、P2、P3、P4、P5中任意相邻3点一阶邻近关系不变，则点P0与点P1、P2、P3、P4、P5中每一点一阶邻近关系不变。因此，研究不改变原一阶邻近点的活动点移动区域，首先研究在保持活动点与任意3个非共线点的邻近关系不变的情况下，活动点P0的移动范围。

2.1.1 平面上活动点与3点一阶邻近的定义

定义：如果活动点与3个非共线点当中的每一点一阶邻近，则称该活动点与该平面3点一阶邻近。

活动点P0与平面3个非共线点Pi－1、Pi、 Pi＋1，如果则

2.1.2 与相邻3点一阶邻近的活动点P0的移动区域

如图2，⊙O为点P3、P4、P5的外接圆，当P0位于⊙O内部时，P0与P3、P4、P5一阶邻近，当P0移动到外接圆上时，线段P3P4的垂直平分线与线段P4P5的垂直平分线相交于圆心点O，这时，P0、P3、P4、P54点共圆，点P0与点P4的Voronoi区域边界只交于一点O，改变了二者的邻近关系，点P0仅与点P3、P5一阶邻近。随着P0移出到圆外部，点P0、P4的Voronoi区域边界交集为空，表示二者仍非一阶邻近关系。可见，点P0与点P3、P4、P5是否一阶邻近，主要取决于P0点与点P3、P4、P5外接圆的位置关系［13］。

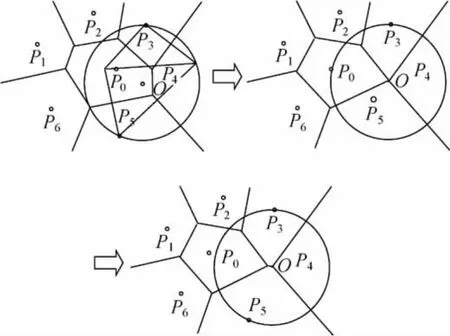
图2 活动点P0位置变化对邻近关系的影响Fig.2 The change of position of the point P0may affect the neighboring relations between the points in the plane

引理：与平面上点Pi－1、Pi、Pi＋1一阶邻近的所有P0点的集合（A1（i））等于以点Pi－1、Pi、Pi＋1为顶点的△Pi－1PiPi＋1的外接圆内部点集（A1（i）circlr）与以△Pi－1PiPi＋1顶点为起点的三角形两边反向延长线所夹区域内点集 （A1（i）sectioni）的并集。如图3所示

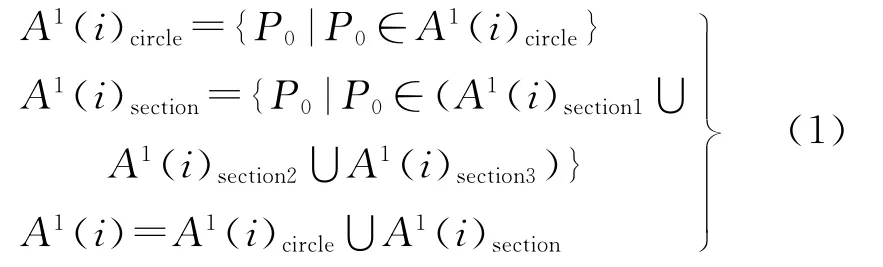
图3 与已知3点一阶邻近的活动点P0的移动范围Fig.3 The moving range of point P0which is neighbor to the three points

证明：

（1）如图4（a），当P0位于△Pi－1PiPi＋1的外部、外接圆的内部时（称该区域为：A11（i）circle＝｛P0｜（P0∈A1（i）circle）∧（P0∉A1（i）△Pi－1PiPi＋1）｝），根据Delaunay三角网的空圆规则［9］，△Pi－1PiPi＋1不能作为Delaunay三角网的一个三角形，△Pi－1PiPi＋1的任意一条边不能作为点P0、Pi－1、Pi、Pi＋1所形成的凸四边形的对角线，亦即，点P0与点Pi－1、Pi、Pi＋1分别有一条Delaunay三角形的边相连，则点P0与点Pi－1、Pi、Pi＋1必然一阶邻近。

（2）如图4（b），当点P0在△Pi－1PiPi＋1的内部或边上时（称之为区域A21（i）circle＝｛P0｜P0∈A1（i）△Pi－1PiPi＋1｝）。同 样，根 据 空 圆 规 则，△Pi－1PiPi＋1不能作为Delaunay三角网的一个三角形，需要对其重新剖分，在三角形内部及边上一点对该三角形进行剖分有且只有一种剖分结果，就是将该点分别与原三角形的三个顶点相连，线段P0Pi－1、P0Pi、P0Pi＋1就分别成为Delaunay三角形的一条边，因而点P0分别与点Pi－1、Pi、Pi＋1一阶邻近。

（3）如图4（c），当点P0位于A1（i）section1、A1（i）section2或A1（i）section3内部（即P0∈A1（i）section），同样由于点Pi－1、Pi、Pi＋1外接圆为空圆，因而，△Pi－1PiPi＋1可以作为Delaunay三角网的一个三角形。图中，由于点P0位于线段Pi－1Pi、Pi＋1Pi延长线所形成的扇形区域（不包括延长线上的点）内，点Pi必然位于△Pi－1P0Pi＋1中，以点Pi对△Pi－1P0Pi＋1进行剖分，则P0点与点Pi－1、Pi、Pi＋1的连线分别为Delaunay的一条边，因而P0点分别与点Pi－1、Pi、Pi＋1一阶邻近。

（4）如图4（d），当点P0位于A1（i）区域外时，即P0∈（A1（i））－，由于△Pi－1PiPi＋1外接圆为空圆，因而△Pi－1PiPi＋1可以作为Delaunay三角网的一个三角形，点P0与点Pi－1、Pi、Pi＋1可以形成一个以△Pi－1PiPi＋1的边为对角线的凸四边形，P0只能和其最近的△Pi－1PiPi＋1的两个顶点相连构成新的三角形，与△Pi－1PiPi＋1的另外一个顶点没有边相连，不具有一阶邻近关系。

由于平面点的全集S＝A1（i）∪（A1（i））－＝A1（i）circle∪A1（i）section∪（A1（i））－＝A11（i）circle∪A21（i）circle∪A1（i）section∪（A1（i））－，以上讨论的4类区域的并集代表整个平面区域，因而，A1（i）＝A1（i）circle∪A1（i）section可以完备地表示平面上与点Pi－1、Pi、Pi＋1相邻的点P0的集合。

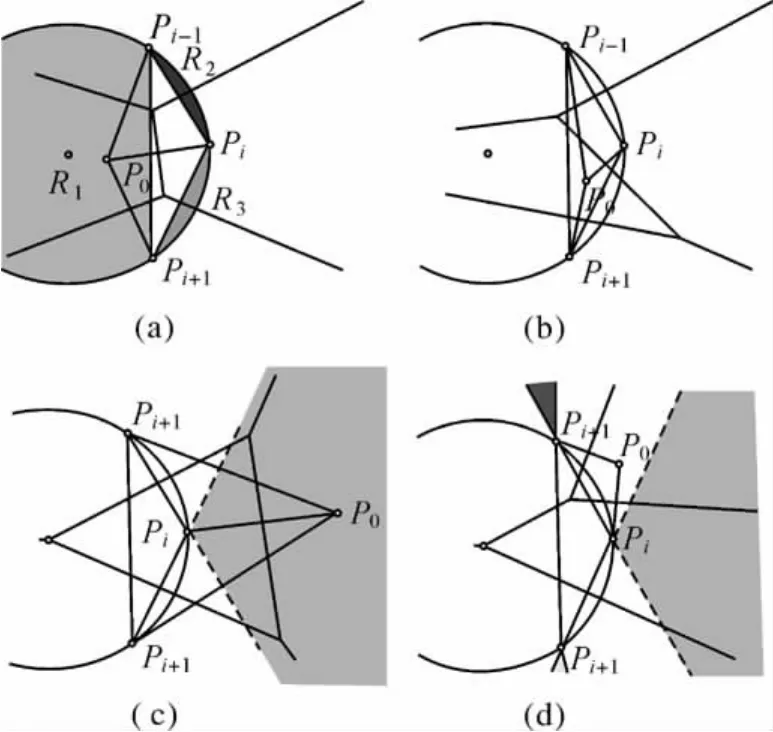
图4 平面上不同区域活动点与已知3点的邻近关系Fig.4 The neighboring relations between the point P0 and the other three points of the plane in the different area

以上证明了与一阶邻近多边形连续3个顶点保持邻近关系的点P0的活动区域，若保证点P0与其一阶邻近多边形中每一顶点都一阶邻近，显然，P0应该处在其一阶邻近多边形每连续3顶点所确定区域A1（i）的交集内。

结论1：若P0与n个一阶邻近点的一阶邻近关系保持不变，则P0点必须位于其n个一阶邻近点中依次相邻3个一阶邻近点所形成的n个A1（i）区域的交集内。

设Pi（1，2，…，n）为P0点的一阶邻近点，相邻一阶邻近点Pn、P1、P2，P1、P2、P3，P2、P3、P4，…，Pi、Pi＋1、Pi＋2，…，Pn－2、Pn－1、Pn，Pn－1、Pn、P1的A1（i）区域分别为A1（1）、A1（2）、…、A1（n），则

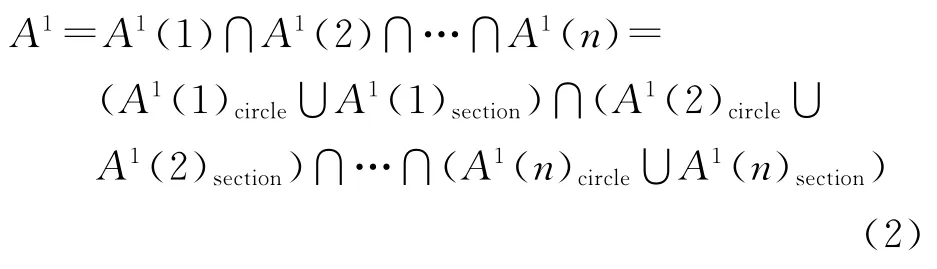
2.2 不产生新的一阶邻近点的活动点P0的移动区域

结论1所确定的区域A1只能保证在点P0移动过程中保持与原有一阶邻近点的邻近关系不变，但不能保证其没有新的一阶邻近点产生。随着P0点的移动，尽管其与原有一阶邻近点的邻近关系不变，但其可能与原二阶邻近点形成新的一阶邻近关系，其一阶邻近点数目增加，一阶邻近多边形由于顶点数目增加而发生变化。那么，活动点P0与原一阶邻近点邻近关系不变的情况下，进一步研究是否有新的一阶邻近点产生。

如图5（a）所示，在点P0移动之前，其邻近多边形顶点为点P1、P2、P3、P4、P5，线段P4P5为一阶邻近多边形的一条边，点P4、P5共同的一阶邻近点为点P0和P6。点P0位于△P4P5P6的外接圆外部，与点P6是二阶邻近关系，此时，点P0、P4、P5、P64点满足空外接圆规则，线段P4P5为4点所构成四边形的对角线。当P0点移动到△P4P5P6外接圆及其内部时（P′0点位置），空圆规则破坏，需要对四边形重新剖分，交换对角线，此时点P0与点P6成为Delaunay三角形的一条边，点P6成为点P0的一阶邻近点，形成如图5（b）所示的P0点新的一阶邻近多边形P1P2P3P4P5P6。可以看出，要保证P0点邻近多边形的边不变，没有新的一阶邻近点加入，P0点必须位于该边两端点及其除P0点以外的另一共同一阶邻近点所确定外接圆的外部。

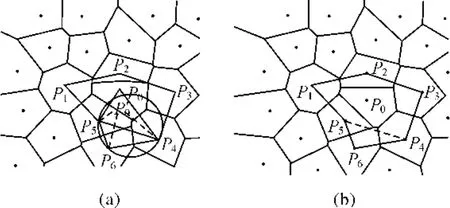
图5 P0点移动导致其邻近多变形变化图Fig.5 The moving of the point P0may change it’s neighboring polygon

结论2：点P0在A1区域内移动时要确保其没有新的一阶邻近点产生，则P0点应保持在该边两端点及其除P0点以外的另一共同一阶邻近点所确定外接圆的外部（必要条件）。

设P0点邻近多边形ADJpolygon（P0）的边PjPj＋1的两个端点Pj、Pj＋1与该两点在邻近多边形外侧的共同一阶邻近点的外接圆区域为A2（j）circlr，则在满足条件的P0点的活动区域可以表示为

2.3 活动点拓扑邻近稳定区域的确定

结论2只是保持P0点一阶邻近多边形不变的必要条件。如图6（a）中的绿色区域为满足结论2的P0点移动范围；图6（b）表示当P0点在绿色区域中移动时，其邻近多边形发生了变化，改变原一阶邻近的一阶邻近关系。可见，如果P0点移动后只满足结论1，虽然可以保持原有一阶邻近点不变，但可增加新的一阶邻近点；如果只满足结论2，尽管可以确保不会增加一阶邻近点，可是会造成原有一阶邻近点数目减少。可见，要保证P0点移动后，其一阶邻近点既不增加又不减少，P0点必须同时满足结论1与结论2的条件。

图6 仅满足结论2的效果图Fig.6 The result of conclusion 2

结论3：若保持P0点的一阶邻近多边形不变，P0点必须位于A1区域与A2区域的交集内。

图7、图8为利用结论3确定的拓扑稳定区域。

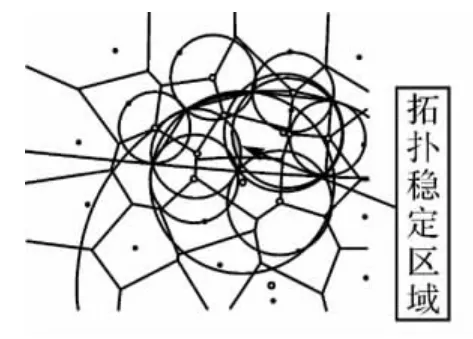
图7 结论3所确定的P0点的拓扑稳定区域Fig.7 The topology stable area of point P0 defined by conclusion 3

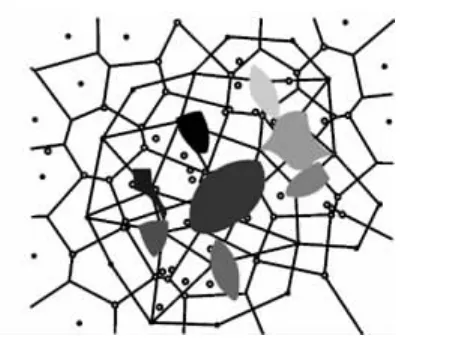
图8 结论3所确定的离散点的拓扑稳定区域Fig.8 The topology stable areas of the plane discrete points defined by conclusion 3

3 活动点拓扑邻近稳定区域的计算

根据结论3，可以给出活动点拓扑邻近稳定区域的计算模型。

如图9，设点P0为扇形区域A1（i）section中任意一点，则向量P（i＋1）Pi与PiP0的夹角β1，向量PiP0与P（i－1）Pi的夹角β2，向量P（i＋1）Pi与P（i－1）Pi的夹角β存在以下关系

式中，K（i＋1）－i表示过点Pi＋1、Pi的直线的斜率，其计算公式为

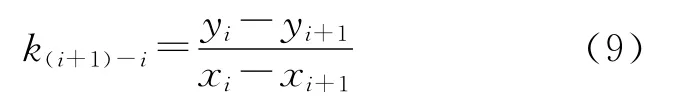
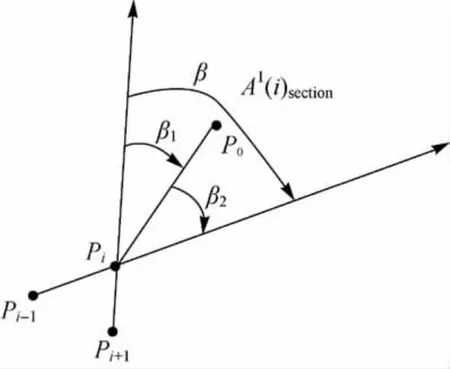
图9 扇形区域内点满足的条件Fig.9 The condition must be met by the points in the sector

将式（6）、（7）、（8）代入式（5），得到式（10），则A1（i）section中点P0坐标一定满足该等式标和半径分别为设P0点一阶邻近多边形ADJpolygon（P0）的边PiPi＋1的两个端点Pi、Pi＋1除P0点外的另一个共同一阶邻近点Pj的坐标为（xj，yj），Pi、Pi＋1、Pj圆心坐标和半径分别为则P0点坐标（x，y）为满足以下方程的解

设点Pi（1，2，…，n）为点P0（x，y）的一阶邻近点，其坐标为（xi，yi），△PnP1P2、△P1P2P3、△Pi－1PiPi＋1、…、△Pn－1PnP1的外接圆圆心坐

4 试 验

采用本文方法和逐点试探法分别绘制移动点P0的拓扑稳定区域，进一步验证结论3的正确性。图10是按照该方法，即利用式（11）绘出的移动点P0的拓扑稳定区域。图11为逐点试探所确定的移动点P0的拓扑稳定区域，是以保持P0点的一阶邻近多边形不变为约束条件，以邻近多边形内的每一点代替P0，生成Voronoi图及邻近关系，判断P0点的邻近多边形是否变化，如果不变则记录下该点，最后绘出满足条件的所有P0点。试验证明两种方法绘出的满足条件的P0点的区域是等价的，验证结论3的正确性。

图10 采用本文方法得到的拓扑稳定区域Fig.10 Topology stable area generated by above method

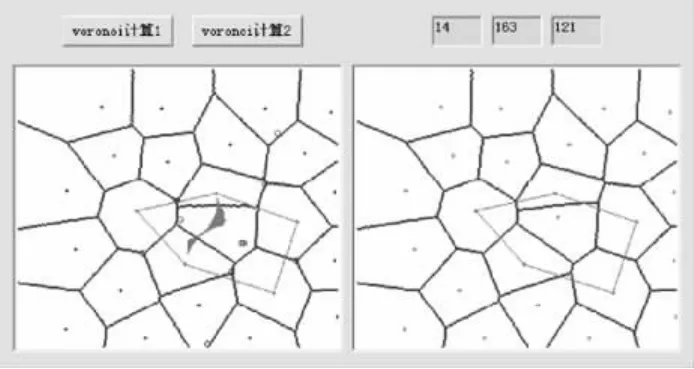
图11 采用逐点试探法得到的拓扑稳定区域Fig.11 Topology stable area generated by the one by one trying method

5 结 论

提出在平面离散点集中每一点的周围存在一个拓扑邻近稳定区域，并给出其计算方法。点的拓扑邻近稳定区域计算之后，在点移动过程中，不需要重构Voronoi图或Delaunay三角网即可判断其与周围各点的邻近关系，同时利用点的拓扑邻近稳定区域可以在确保点的邻近关系不变的情况下，进行相关条件约束下的点目标位置最优规划。线目标和面目标可看做由一系列点连接而成［14－15］。将对基于点的拓扑邻近稳定区域计算模型对线和面的拓扑邻近稳定区域计算方法作进一步研究。

［1］ GOLD C M.Spatial Adjacency a General Approach［EB／OL］.［2005－03－18］.http：∥www.voronoi.com／wiki／images／a／ae／Spatial＿adjacency－a＿general＿approach.pdf.

［2］ GOLD C M.The Meaning of“Neighbour”［C］∥Proceedings International Conference GIS：Theories and Methods of Spatial－temporal Reasoning in Geographic Space.Berlin：Springer－Verlag，1992：220－235.

［3］ CHARISTOPHER B J，GERAINT L B，WARE J M.Map Generalization with a Triangulated Data Structure［J］.Cartography and GIS，1995，22（4）：317－331.

［4］ TSAL V J D.Delaunay Triangulations in TIN Creation：an Overview and a Linear－time Algorithm［J］.International Journal of Geographical Information Systems，1993，7（6）：501－524.

［5］ WEIBEL R，JONES C B.Computational Perspectives on Map Generalization Guest Editorial for Special［J］.Geo－Informatica，1998，2（4）：307－314.

［6］ AI Tinghua，LIU Yaolin.A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved［J］.Acta Geodaetica et Cartographica Sinica，2002，31（2）：175－181.（艾廷华，刘耀林.保持空间分布特征的群点化简方法［J］.测绘学报，2002，31（2）：175－181.）

［7］ YANG W.The Design of a Dynamic Voronoi Map Object（VMO）Model for Sustainable Forestry Data Management［D］.Laval：Laval University，1997.

［8］ CHEN Jun.The Voronoi Dynamic Spatial Data Model［M］.Beijing：Surveying and Mapping Press，2002.（陈军.Voronoi动态空间数据模型［M］.北京：测绘出版社，2002.）

［9］ W ANG P.Automated Generalization in GIS［M］.Wageningen：Agricultural University and ITC，1997.

［10］ GOLD C M，YANG W.Spatial Data Management Tools Based on the Voronoi Dynamic Data Model（Vordll 1.0）User’s Manual［R］.Laval：Laval University，1994.

［11］ MAO Jianhua，CHEN Fei，MAO Duanqian.A Method for Detecting the Topological Relations’Change of the Moving Object［J］.Bulletin of Surveying and Mapping，2003（4）：22－24.（毛建华，陈斐，毛端谦.地图目标移位的拓扑关系变化检测方法［J］.测绘通报，2003（4）：22－24.）

［12］ LEDOUX H，GOLD C M.A Voronoi－based Map Algebra［EB／OL］.［2005－03－18］.http：∥www.voronoi.com／wiki／images／0／0f／Voronoi＿map＿algebra.pdf.

［13］ MIOC D，ANTON F，GOLD C M，et al.Map Updates in a Dynamic Voronoi Data Structure［EB／OL］.［2005－03－18］.http：∥www.voronoi.com／wiki／images／0／0f／map updates in a dynamic voronoi data structure.pdf.

［14］ CHEN Jun，LIU Wanzeng，LI Zhilin，et al.The Refined Calculation Method of Topological Relationships between Line Objects［J］.Acta Geodaetica et Cartographica Sinica，2006，35（8）：255－260.（陈军，刘万增，李志林，等.线目标间拓扑关系的细化计算方法［J］.测绘学报，2006，35（3）：255－260.）

［15］ XIE Shunping，FENG Xuezhi，LU Wei.Algorithm for Constructing Voronoi Area Diagram Based on Road Network Analysis［J］.Acta Geodaetica et Cartographica Sinica，2010，39（1）：88－94.（谢顺平，冯学智，鲁伟.基于道路网络分析的Voronoi面域图构建算法［J］.测绘学报，2010，39（1）：88－94.）