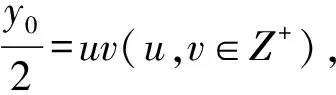杜先存,史家银，赵金娥

(1.红河学院 教师教育学院，云南 蒙自 661199；2.云南艺术学院 艺术文化学院，云南 昆明 650033；3.红河学院 数学系，云南 蒙自 661199)

关于Pell方程x2-Dy2=±1(D是非完全平方的正整数)的整数解问题,文献[1-4]已有一些结果,而关于Pell方程x2-aby2=-1(ab是非完全平方的正整数)的整数解问题,文献[6-8]已有一些结果.文献[7]利用奇偶性、同余性和Legendre符号的性质等给出了p>3是一个Fermat素数时,Pell方程x2-5py2=-1有正整数解.本文则利用奇偶性、同余性和完全平方数的性质等将文献[7]的方程x2-5py2=-1中的条件“p>3是一个Fermat素数”推广到“p为5n±2(n≡-1(mod4))型的素数”,即探讨Pell方程x2-5(5n+2)y2=-1与x2-5·(5n-2)y2=-1(n∈Z+,n≡-1(mod4),5n-2为素数)的解的情况.

1 主要结论

定理1 Pell方程：

x2-5(5n+2)y2=-1(n∈Z+,n≡-1(mod4),5n+2为素数)

(1)

有正整数解.

定理2 Pell方程:

x2-5(5n-2)y2=-1(n∈Z+,n≡-1(mod4),5n-2为素数)

(2)

有正整数解.

2 定理证明

2.1 定理1证明

证明设(x0,y0)是x2-5(5n+2)y2=1的基本解,若x0为偶数,则x02≡0(mod4).

因为n≡-1(mod4),令n=4k-1(k∈Z+),则5(5n+2)=5[5(4k-1)+2]=100k-15=4(25k-4)+1,故有:

x02-5(5n+2)y02≡-y02(mod4)

(3)

若y0为偶数,则y02≡0(mod4),故(1)为x02-5(5n+2)y02≡0(mod4)；

若y0为奇数,则y02≡1(mod4),又4(25k-4)+1≡1(mod4),故式(1)为x02-5(5n+2)y02≡-1(mod4).

由x02-1=5(5n+2)y02,得(x0-1)(x0+1)=5(5n+2)y02,所以有:

(4)

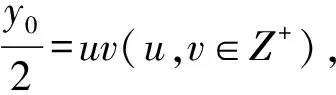
(5)

故式(5)的解只可能为以下4种情况：

上面4种情况可表为：

甲：u2-5(5n+2)v2=1,y0=2uv(u,v∈Z+)，乙：5u2-(5n+2)v2=1,y0=2uv(u,v∈Z+)，

丙：(5n+2)u2-5v2=1,y0=2uv(u,v∈Z+)，丁：v2-5(5n+2)u2=-1,y0=2uv(u,v∈Z+).

若甲成立，则有u2-5(5n+2)v2=1,故(u,v)为x2-5(5n+2)y2=1的解,又y0=2uv(u,v∈Z+),则0

若乙成立,则有：

5u2-(5n+2)v2=1,y0=2uv(u,v∈Z+),

(6)

式(6)两边取模5,得：-2v2≡1(mod5)，即(2v)2≡-2≡3(mod5)，则有：

(2v)2=5m+3(m∈N),

(7)

若式(6)有正整数解，则式(7)有正整数解.又式(7)右边5m+3(m∈N)的末尾只能为3,8，而式(7)左边末尾只能为0,4,6，故式(7)无正整数解，所以式(6)无正整数解，故乙不成立.

若丙成立,则有：

(5n+2)u2-5v2=1,y0=2uv(u,v∈Z+),

(8)

式(8)两边取模5,得：2u2≡1(mod5)，即(2u)2≡2(mod5)，则有：

(2u)2=5m+2(m∈N).

(9)

若式(9)有正整数解，则式(8)有正整数解.又式(9)右边5m+2(m∈N)的末尾只能为2,7，而式(9)左边末尾只能为0,4,6，故式(9)无正整数解，所以式(8)无正整数解，故丙不成立.

综上甲、乙、丙都不对,余下的只有丁成立,此时：

v2-5(5n+2)u2=-1,y0=2uv(u,v∈Z+).

(10)

故(v,u)为式(10)的一组解，即为方程(1)的一组解,又u,v∈Z+,所以方程(1)有正整数解.

2.2 定理2证明

由x02-1=5(5n-2)y02,得(x0-1)(x0+1)=5(5n-2)y02,所以有：

(11)

(12)

上面4种情况可表为：

戊：u2-5(5n-2)v2=1,y0=2uv(u,v∈Z+)，己：5u2-(5n-2)v2=1,y0=2uv(u,v∈Z+),

庚：(5n-2)u2-5v2=1,y0=2uv(u,v∈Z+)，辛：v2-5(5n-2)u2=-1,y0=2uv(u,v∈Z+).

若戊成立,则有u2-5(5n-2)v2=1,故(u,v)为x2-5(5n-2)y2=1的解,又y0=2uv(u,v∈Z+),则0

若己成立,则有：

5u2-(5n-2)v2=1,y0=2uv(u,v∈Z+)

(13)

式(13)两边取模5,得：2v2≡1(mod5)，即(2v)2≡2(mod5)，则有：

(2v)2=5m+2(m∈N)

(14)

若式(13)有正整数解，则式(14)有正整数解.又式(14)右边5m+2(m∈N)的末尾只能为2,7，而式(14)左边末尾只能为0,4,6，故式(14)无正整数解，所以式(13)无正整数解，故己不成立.

若庚成立,则有：

(5n-2)u2-5v2=1,y0=2uv(u,v∈Z+).

(15)

式(15)两边取模5,得：-2u2≡1(mod5)，即(2u)2≡-2≡3(mod5)，则有：

(2u)2=5m+3(m∈N).

(16)

若式(15)有正整数解，则式(16)有正整数解.又式(16)右边5m+3(m∈N)的末尾只能为3,8，而式(16)左边末尾只能为0,4,6，故式(16)无正整数解，所以式(15)无正整数解，故庚不成立.

综上戊、己、庚都不对,余下的只有辛成立,此时：

v2-5(5n-2)u2=-1,y0=2uv(u,v∈Z+).

(17)

故(v,u)为式(17)的一组解，即为方程(2)的一组解,又u,v∈Z+,所以方程(2)有正整数解.

[1] 郑惠,杨仕春.关于Pell方程x2-Dy2=-1可解性的一个判别条件[J].西南民族大学学报:自然科学版，2011,37(4):48-50.

[2] 柳杨.关于不定方程x2-Dy2=-1的解的确定[J].云南民族大学学报:自然科学版，2006,15(2): 91-92,95.

[3] 刘清,陈秉龙.关于Pell方程x2-Dy2=±1的解法[J].农垦师专学报，1997(4):53-56.

[4] 邓波.关于Pell方程x2-dy2=-1的几个结果[J].贵州科学，1994,12(4):64-66.

[5] 陈克瀛.Pell方程x2-2py2=-1(p≡1(mod8)是素数[J].温州师范学院学报，1998(3):1-4.

[6] 陈克瀛.关于Pell方程x2-2py2=-1[J].温州师范学院学报，1996(6):17-19.

[7] 管训贵.关于Pell方程x2-5py2=-1[J].西安文理学院学报，2010(3)：32-33.

[8] 杜先存.Pell方程ax2-by2=1有最小解[J].湖北民族学院学报:自然科学版,2012,30(1):35-38.