黄永畅 何 斌 黄昌宇 杨士林 宋加民

1)(北京工业大学理论物理研究所，北京 100124)

2)(北京工业大学应用数学研究所，北京 100124)

3)(北京大学物理学院，北京 100871)

因果代数及其在物理学中的应用*

黄永畅何 斌1)2)黄昌宇3)杨士林2)宋加民1)

1)(北京工业大学理论物理研究所，北京 100124)

2)(北京工业大学应用数学研究所，北京 100124)

3)(北京大学物理学院，北京 100871)

(2009年2月2日收到;2010年5月18日收到修改稿)

依据定量因果原理，给出了物理学中的一个因果代数的应用，当满足定量因果原理的互逆可消条件且又满足消去律的解时，得到因果分解代数;由因果分解代数导出了结合律和单位元，进而导出了因果分解代数又具有群的结构特征，同时给出了这新代数系统在高能物理学中的应用.严格地给出了在高能物理中既不是群又不是环的反应，发现因果代数和因果分解代数是严格描述粒子物理反应的基本工具，得到了所有各种相加性、相乘性物理量和各种粒子反应都必须满足的统一恒等式，给出了因果代数和因果分解代数对高能物理的具体应用.利用因果代数的表示和超对称的R数，得到了含有超对称粒子反应中相乘性的超对称的PR=(-1)R对称性.还得到了一个关于电子自旋角动量的任意分量间的一个对称关系式，利用这对称关系式，可以化简多电子相互作用的计算.利用互逆可消条件定义了一般的逆元，可重新定义群，使群的公理减少一个，消除了重复定义.

对称性，群论，因果原理，粒子物理

PACS:02.10.De，02.20.-a，13.30.-a

1.引 言

人们在研究自然现象中，从不同程度，不同方面都发现了不同特征的对称性，对称性在物理研究中起着重要作用.例如，四种相互作用的规范场理论的建立和基本粒子的发现.这些对称性都能用群［1］来描述.物理上，为什么物质结构和物质运动中会出现如此多的对称性?这会不会有其更一般的原因在支配?文献［2］一般性地利用定量因果原理给出了不同积分型变分原理的统一，克服了变分原理与相互作用的局域性因果原理不能统一的困难，得到了变分原理和相互作用的局域性因果原理的统一理论，并显示了任一体系中物质转化过程中的不失不得的定量因果原理(简称为定量因果原理).牛顿力学具有绝对时空中的因果关系，量子力学具有统计性的因态演化所致的统计性的因果关系.因果性表示有因果关系事件间一种必然的联系性，而偶然性意味着不确定性.因果的决定性指的是条件与结果之间确定的对应关系.统计力学中出现的随机性一方面是由于我们的认识的不完备造成的;另一方面量子力学揭示出了微观粒子的“内禀”概率特性，而且一些学者认为量子力学中的随机性部分地也是由于我们知识的不完备(如隐参数理论)造成的.

宇宙中各种事物的演化发展的规律，须满足一定的因果关系，且其因果关系必须是定量的.满足定量因果原理是现代宇宙学及一切其他科学的基本出发点.文献［3］给出了定量因果原理对宇宙演化方程的应用，文献［4］依据定量因果关系原理，利用一般的物质流形，给出了理想态、参考态和变形态的统一描述，获得了弯曲空间中应变张量一般表示.更一般地说，而且不同的物理过程也是满足定量因果原理的过程［5］.

对半群、群、环、域和模而言，不同性质的单位元对它们有不同的影响，对这些代数结构的研究，人们仍在不断地探索，并获得了许多重要的结论［6—8］，本文是从一个新的角度来推广研究，以使上述不同代数系统有相应的发展.

人们已知群论中元素满足4个相互独立的公理的集合形成群，而我们发现这4个公理可从这定量因果原理导出.

人们通常依据严格的数学的逻辑演绎体系，先归纳出基本原理(或称公理)，并由这些原理导出若干引理和定理，再由这若干引理和定理导出一个逻辑的演绎体系，最后再将所得演绎体系用到实际中去，从而形成一个实用的理论体系.本文依据严格的数学的逻辑演绎体系，先归纳出一个基本原理，并由这些原理导出若干引理和定理，再由这若干引理和定理导出一个逻辑的演绎体系，最后再将所得演绎体系用到物理实际中去，从而形成一个实用的理论体系.

2.定量因果原理对因果代数系统的描述

满足因果原理是一切科学的基本要求.因为从物质间相互作用的因果关系来看，其间必有物质传递和转换，其传递的物质或物质的转换不会凭空增加或减少，而这正是宇宙中得失相等的定量因果关系原理或称为定量的因果转换关系原理的一种表述，则有定量因果关系原理的一个数学表示为［2，3］

式中S为一个表征体系特征量的集合，D，C可为不同算子函数的集合.(1)式的意义是:任意一类算子函数D对集合S作用，其所能出现的真实的物理结果必导致体系对应的某一类特征量C的出现，使其在定量上满足D(S)=CS(D(S)表示算子函数D对S求一般的算子作用函数D(S)，其一个简单的情况是D(S)=DS)，整个过程满足任意一些量的定量作用(因)，必导致相应等量因的果，也就是满足不失不得的定量因果关系原理［2，3］.C由(1)式确定，可由不同方式得到.由定量因果原理可给出某些代数或几何系统的有效描述.这也因群、环、域自然地包含在模中［9］，而模是(1)式的特例［9，10］，线性空间是模的特例［9］，微分流形局域是同胚于线性的欧氏空间［11］，纤维丛是微分底流形上赋有纤维空间的推广［12，13］，表征物理学中基本相互作用规律的规范场正是主纤维丛的联络［12，13］，其联络的获得正是(1)式中D为联络算子，S为截面，C=ω为联络的特例［13］，而粒子物理学中的各种基本相互作用恰是通过各种规范场的作用来实现的，故定量因果原理的作用对粒子物理学的研究而言是相当重要的.对 Hopf代数、量子群等的研究，文献［14，15］所给出的代数也是满足因果关系的代数.由于我们在此要考虑的是群的概念的推广，故在数学上(1)式中的D，C，S可被简化为一个集合中的不同元素，如可定义为群的元素.事实上，一种代数正是满足某些逻辑和定量运算规则的一些元素的一种集合［6，9］，如群就是一些元素满足一种群运算规则的一种代数，之所以要推广群到一般代数是因为有大量的物理系统没有群的对称性，有比群更小的对称性(如半群).故研究这些更小的对称性就具有重要的物理意义.

在定量因果原理表达式(1)中，当D=S为一个非空集合，当C为单位算符，则DS=S，所以，(1)式恰为封闭性.因此，我们一般地导出封闭性定理如下，

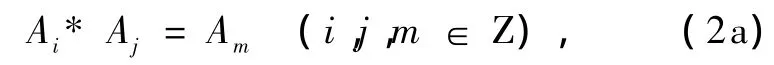
此式相当于对Aj(或Ai)作定量Ai(或Aj)的左(或右)传递作用到Am.又由(2a)式的封闭性总有

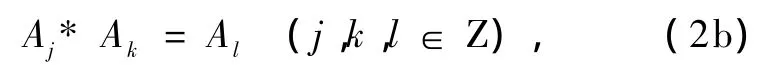
我们可从(1)式一般地导出(或定义)存在广义逆元Am，即:Aj(或Am)与Ak(∈S)左作用，然后是Ai与Am(或与Aj)左作用，再与已得的(Aj*Ak) (或(Am*Ak))左作用，得D对S操作，数学上表示对S求一般的函数D(S)={(Ai*Am)*(Aj* Ak)}(由于 Ai，Aj，Am，Ak∈S)(或={(Ai*Aj)* (Am*Ak)})，且当C=S，即CS={Ai*Ak}，我们获得如下定理:

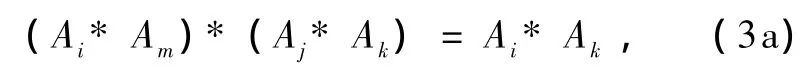
或

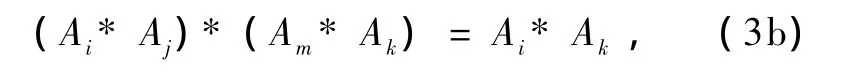
即这定理一般地定义了满足(3a)或(3b)式的广义逆元Am.(其中(ⅳ′)不是按照出现的次序标记，而是按照群论通常意义公理的习惯标记，下同)事实上，从(3a)和(3b)式可以看出Am和Aj互为逆元，因而它们是相关的.又由于(3a)和(3b)式是一般的，即对任意的Ai，Ak∈S，(3a)和(3b)式都成立.

在方程(3a)中取Aj为Am，则相关的原Am要记为(Am)-1，故得(Ai*(Am)-1)*(Am*Ak)=Ai*Ak(3a′)，这里记号(Am)-1是表示与Am有关的S中的某个元素.如果这互逆可消条件是次序无关的，则这系统对(3a)和(3b)同时满足，如果还满足消去律，则由(3a)和(3b)可得(Am)-1=Aj;反之亦然.因此，Am为广义逆元A-1j.

所以，由(3)式可得

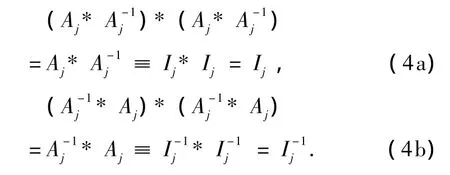
进一步由(3)，(4)式可得

定理(ⅲ′)

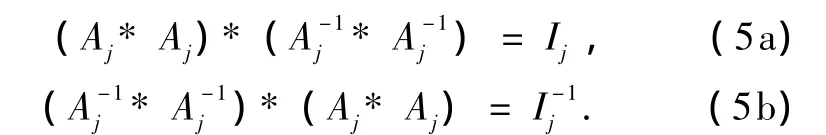
由Ai和Aj的任意性，利用(2b)，(3)和(4)式得:Aj，A-1

j，Ak，Al，

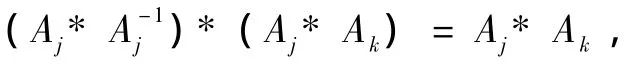
即

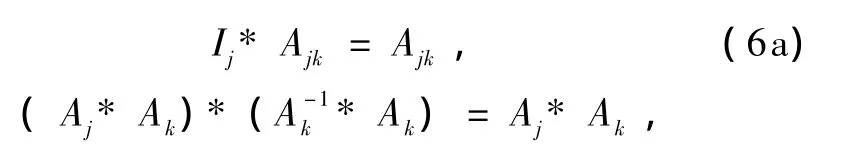
即

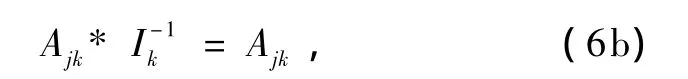
其中 Ij分别为左、右关联单位元，因此，我们自然地得到了左、右关联单位元，它们满足一种新单位元的二元运算性质.这是所推导出有意义的新结果之一.

定理(ⅳ′)的另一个直观的意义是(Ai*Aj)和中分别有Aj和A-1j的作用，则(3)式中Aj和的正反互逆作用可抵消.

由于以上讨论形成一个一般的代数系统，并且所导出的(2)和(3)式满足定量因果原理，故称满足(2)和(3)式的代数为因果代数，而(4)—(6)式只是(2)和(3)式的推论.

3.因果分解代数系统和群的关系

在因果代数中，当满足具有一般特性的消去律时，也就是可分解时，即(3a)可简化为

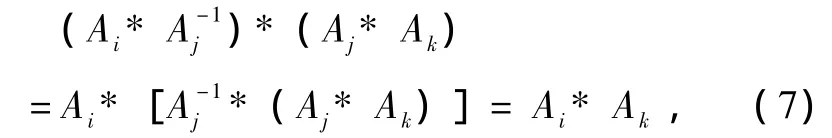
或

要特别说明的是:对(1)式而言，D(S)=(Ai*Aj)*为一个一般情况，此时D(S)=DS=［(Ai为一个简化情况.事实上，(7)或 (8)式分别是互逆可消条件的一个消去条件，则可得简化的互逆可消条件

定理(ⅳ″)

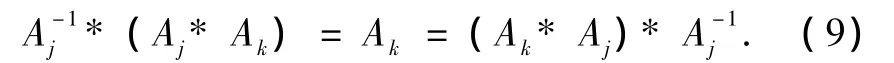
由于定理(ⅳ″)是在消去条件存在从而可分解(3)式下成立的解，故因果代数此时转变，可称为因果分解代数.

现证由(ⅰ)，(ⅳ′)和(ⅳ″)定理条件可导出结合定理(或仅从群论讲叫结合律).

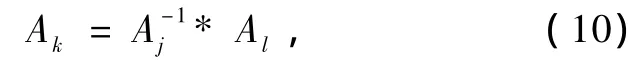
用Am左乘(10)式，同时把(2a)式代入，并利用(3)式，得一个重要的公式

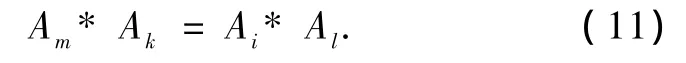
用(2a)和(2b)式代入(11)式，得结合律定理(ⅳ)

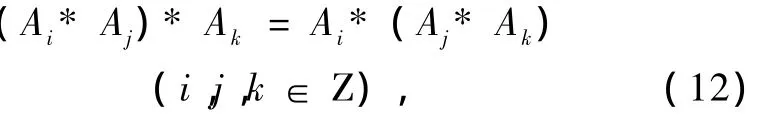
即可由定理(ⅰ)，(ⅳ′)和(ⅳ″)导出结合律，其命题得证.也就是说对因果分解代数而言，自然包含结合律，而由因果代数不能导出结合律.

下面可证明在因果分解代数中 A-1i为Ai的更直接意义下的逆元，并且可证 Ai*A-1i为S中的单位元.由于现在是在因果分解代数中讨论，故可利用导出的结合律，则(9)式可写为

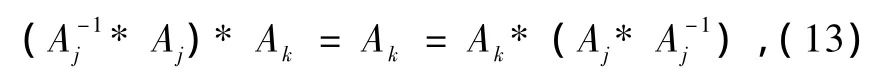
可见(13)式比(3)式有更直接意义的逆元表示.

一方面利用(13)式的第二个等式可得

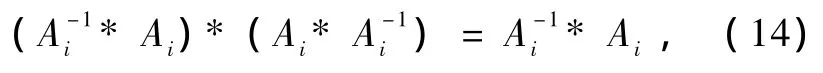
另一方面利用(13)式的第一个等式又可得

因此得

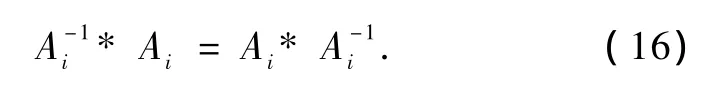
可见在因果分解代数中Ii=I-1i.

利用(13)和(16)式，可得

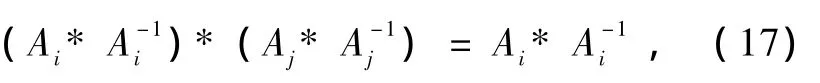
另一方面利用(13)式，可得

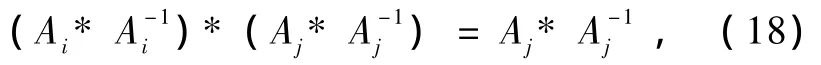
定理(ⅱ)

则(13)式变为

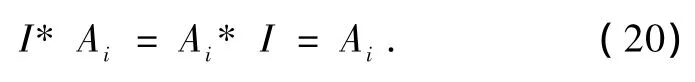
由导出的(19)和(20)式可知，A-1i为Ai的逆元(ⅱ)，Ⅰ为单位元(ⅲ).由定理(ⅰ)，(ⅳ)，(19)和(20)式得此时 S为群.可见因果分解代数与群等价，故综合以上讨论可发现事实上对称性来源于定量因果原理.特别是以上的研究使我们更深刻地理解了单位元的内部结构和作用.另一方面，显然由群推不出因果代数，但模仿本文的讨论又可推出这新的因果分解代数，因而本文发现了群具有新的因果分解代数的性质，那么关于群在粒子物理学中的所有应用［16］，因果分解代数可有对应的应用.因此，我们发现了比群的对称性更小的对称性和相关的数学结构，这是过去没有得到过的所推导出有意义的新结果之一.

4.因果代数和因果分解代数与粒子物理学关系的研究

从以上的讨论可见，因果代数的典型特征是满足定理(或仅从群论讲叫公理)(2)(封闭性)和定理(或仅从群论讲叫公理)(3)(互逆可消条件)，公式(4)—(6)只是定理(2)和(3)的推论，而且特别要强调的是在因果代数中不包含结合律，故在因果代数中不能作结合律的运算，但是在因果分解代数中可作结合律的运算.因果代数中的封闭性可表特征系统元素的作用具有可传递性，而互逆可消条件在此时表征这传递一旦产生，可由相应的逆作用来抵消.

如考虑Aj为绕某一轴的转角，而A-1j则为对应的反转角，Ai和Ak也为绕同一轴的不同转角，其运算符*此时表征对应转角的相加，则其封闭性和互逆可消条件成立.

通过对粒子物理学中对称性的认识，可进一步理解物理规律的起源，而且对称性总是和某种变换联系在一起的，并且任何一个封闭物理系统或足够大的物理系统的变化都必须是满足定量因果原理的.物理系统在某个连续对称群的变换下保持不变，由Noether定理可以导出系统具有对应的守恒量.而以上所有这些对称性都是满足定量因果原理的，而且本文由定量因果原理导出了群，特别是定量因果原理可以是逻辑上的定量因果原理，更一般的是绝大多数物理规律总可以由一些方程来表示，方程中一些量变化(因)，必须引起另一些量的变化(果)，以使方程右边保持为零的，即不失不得，因此正是定量因果原理的一种数学表示形式，所以定量因果原理是一般的原理.

在高能物理中，虽然弱作用中的宇称和弱作用中的同位旋不守恒，但它们也是满足某个群的对称性的选择定则的［1，16］，并且相关量的组合(如电荷共轭宇称反演和时间反演(CPT))操作于系统还是满足因果分解代数的，即满足某个群的对称性.而且对高能物理反应中粒子的因果分解代数物理量变化的选择定则所对应的反应，它们是满足群的对称性选择定则的反应，而本文的因果分解代数具有群的性质，上一节已证明对称性来源于定量因果原理.所以，所有关于群对因果分解代数物理量变化的选择定则的反应的应用，同样可以用因果分解代数来进行，即直接可以用群论来研究，这里不再赘述，可参见文献［1］.

利用这电荷共轭宇称反演(CP)部分地破坏程度(定量的原因)可以严格地计算宇宙是如何定量地演化成现在这样以正物质为主宇宙的(定量的结果)［17，18］，即同样是满足定量因果原理.对于弱相互作用中宇称不守恒的反应，依据量子力学，必定存在相应的 Hamilton小量 H′使得跃迁矩阵元不为零，其中和为归一化的初、末态，则由量子力学，对任意的算符H′必有，即此式满足(1)式，其中这是因为初态不为零，则可得同样满足定量因果原理的表示(1)，只是这时的是一般的复合表示.对于其他的不守恒的相互作用也可作类似的讨论，不再重复.分立操作对应的守恒量是相乘性守恒量.

5.因果代数和因果分解代数的应用

下面研究因果代数和因果分解代数在高能物理的粒子反应及粒子碰撞等方面的应用.

由封闭性可导出高能物理中相互作用粒子的一般反应恒等式.由于这些反应都必须满足定量因果原理，所以必定有如下满足定量因果原理的封闭性表示的反应恒等式

(21)式表示在任意两个高能粒子的相互作用所产生的一个粒子的反应中，反应前一个粒子的物理量与另一个粒子的相对应的物理量的“*”作用所得到的量，等于反应后所形成粒子相对应的物理量，即反应前后得到的所对应的总量不变.

由因果代数可导出超对称粒子反应中的物理量必须满足的恒等式.因为超对称粒子间的反应必须满足定量因果原理，所以必定有如下满足定量因果原理的物理量的统一的一般恒等式

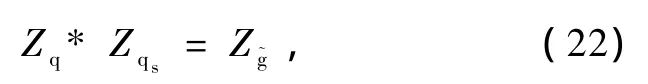
其中Zq，Zqs和Z珓g分别为夸克、超夸克和胶微子的对应一般物理量，如 Z可以分别是电荷、色荷、角动量、宇称、能量和动量等一般量子数，也就是Zq，Zqs和Z珓g可分别记为Ai，Aj和Am，从而满足从定量因果原理导出的(2a)式.当所有因果物理量的守恒量方程(22)都满足时，就可以有如下的超对称粒子的反应能发生［19，20］其中q，qs和分别为夸克、超夸克和胶微子.

对于反应式(23)，利用方程(22)和超对称的R数，即R=3B+L+2S，其中B，L和S分别为粒子的重子数、轻子数和自旋，我们可得到超对称粒子的PR对称，即得到反应式(23)中相乘性的超对称的PR=(-1)R对称性，也就是方程(22)的左右两边粒子的超对称PR的对称性不变，这是可验证的.

例如，考虑反应(23)的PR对称，q，qs和的重子数B、轻子数L和自旋S分别为q(1/3，0，1/2)，qs(-1/3，0，0)和(0，0，1/2)，则我们得到PR(q)PR(qs)=PR()=-1.即此方程中左右两边粒子的相乘性的超对称 PR的对称性不变.故超对称粒子间的反应(23)中具有的物理量必须满足定量因果原理，亦满足定量因果原理所导出的因果代数的表示(21).所以，最后得到了给出所有各种相加性、相乘性物理量和超对称粒子反应式(23)的具体表示都分别必须满足的统一恒等式(22).对其他含有超对称粒子的反应，也可进行相似的讨论，因为含超对称粒子的反应式(21)是一般的，故不再重复.

进一步当存在l和m，使

成立时，则可存在反应

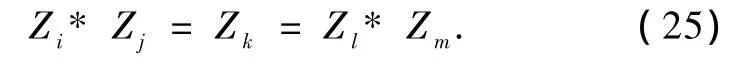
此时Zk为相互作用粒子的物理量所对应反应的中间态，在一些情况下这中间态可称为共振态，而且(25)式也可直接简记为

(26)式表示在任意两个高能粒子的相互作用所产生的两个粒子的反应中，反应前一个粒子的物理量与另一个粒子的相对应物理量的“*”作用所得到的量，等于反应后所形成一个粒子的相对应的物理量与另一个粒子的相对应物理量的“*”作用所得到的量，即反应前后“*”作用所得到的物理量不变.

例如，对于(26)式，它可对应于质子和π-介子相互碰撞的反应，由于它们必须满足定量因果原理，所以同样有如下满足定量因果原理的恒等式

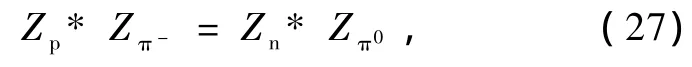
其中Zp，Zπ-，Zn和 Zπ0为质子，π-介子、中子和 π0介子的具有一般特性的物理量，也就是 Zp，Zπ-，Zn和Zπ0可分别记为Ai，Aj，Al和Am，从而满足(26)式，如Z可以分别是电荷、重子数、宇称、G宇称、角动量、能量和动量等.故(26)式给出了它们所有物理量必须满足的统一恒等式，而且对所有的这些物理量，只有当它们相关物理量的恒等式都满足时，才可以有所对应的粒子反应

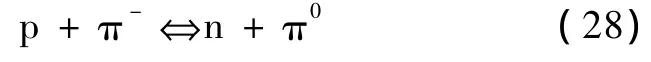
发生，(28)式中相互作用粒子的物理量所对应的反应是可逆的，这也是由于高能物理中两体系统的微观粒子的相互作用是可逆过程.故其中封闭性条件的(24)中初、末态可分别由质子和π-介子与中子和π0介子构成，而且利用封闭性的表示(24)，可以发现这类反应中，它们有对应于Zk的中间态.(28)式表示质子和中子相互碰撞可生成右边的产物，由右边也可生成左边的产物，即表征了反应前后对应的各种物理量的转换是得失相等守恒的.所以我们最后得到了给出所有各种相加性、相乘性物理量和反应式(28)的具体表示都分别必须满足的统一恒等式.故这是一种最直接的与粒子物理学相关的因果代数表示.特别是在高能粒子反应中，存在大量的类似于(26)的反应，不存在左右对称的单位元，却又有特殊相关的逆元(如π-介子)，这样使(28)或(26)—(28)式既不是群(因为在因果代数中没有定义结合律，也导不出结合律)，又不是环，即使到目前为止，世界上还没有一个代数可恰好直接并严格地描述它们，而本文提出的因果代数正好是严格、自然和直接地描述它们真实存在的粒子物理反应的重要工具.而且因果代数在粒子物理学中还有大量的应用，例如在高能粒子族射中，存在大量的这类反应［16］.进一步可利用(24)式中的 Zk作为(26)式中的Zm，则可得多粒子的反应表示式Zi*Zj=Zl*(Zi′*Zm′)，如此多次操作可得更多粒子的一般反应表示式，如Zi*Zj=Zl*(Zi′*(Zi″*Zm″)).

而且互逆可消条件同样也可导出高能物理中物理量必须满足的恒等式.如两粒子的相互碰撞的反应中，由于它们必须满足定量因果原理，所以同样有如下满足定量因果原理的恒等式

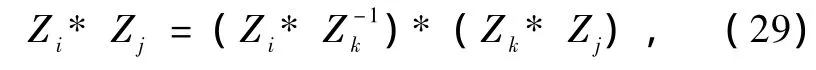
当所考虑的代数为因果分解代数时，则可得

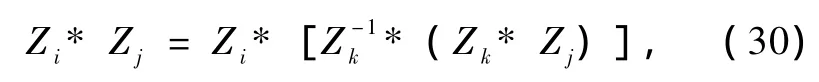
又因为因果分解代数有结合律，则又可有

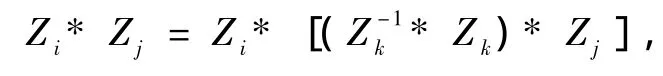
例如在质子和中子相互碰撞的反应中，由于它们必须满足定量因果原理，所以同样有如下满足定量因果原理的恒等式

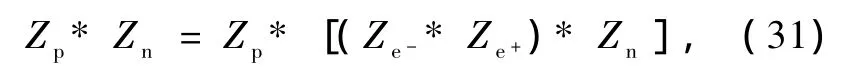
当碰撞的能量更高时，有如下反应:

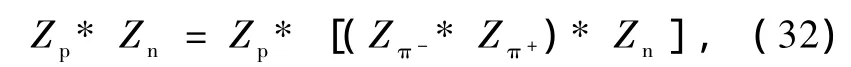
其中Zp，Ze-(Zπ-)，Ze+(Zπ+)和Zn分别为质子、电子(π-介子)、反电子(π+介子)和中子的具有一般特性的物理量，也就是 Zp，Ze-(Zπ-)，Ze+(Zπ+)和Zn可分别记为 Ai，A-1j，Aj和Am，从而满足(3a)式，如Z可以分别是电荷、轻子数、重子数、角动量、宇称、能量和动量等.故(31)和(32)式给出了它们所有物理量必须满足的统一恒等式，而且对所有的这些物理量，只有当它们相关物理量的恒等式都满足时，才可以有所对应的粒子反应

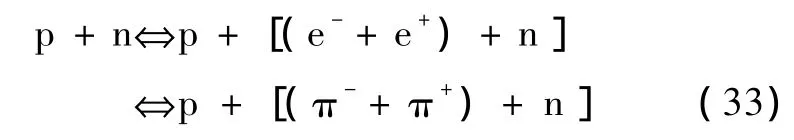
发生，故其中互逆可消条件的 Ai，A-1j，Aj和Ak可分别记为质子、电子(π-介子)、反电子(π+介子)和中子，(33)式表示质子和中子相互碰撞可生成右边的产物，由右边也可生成左边的产物，即表征了反应前后对应的物理量的转换是得失相等守恒的.所以我们最后得到了给出所有各种相加性、相乘性物理量和反应式(33)的具体表示都分别必须满足的统一恒等式.这是所推导出有物理意义的结果之一.

特别是点粒子的相互作用可以用超弦理论中具有更高维的粒子——弦来更一般地描述，故(ⅰ)，(7)和(8)式可以用来作为更一般地判断超弦理论中不同弦间的反应能否发生的判据.因为在超弦理论中，粒子的存在形式是其弦的不同的振动的模式［21］，当选Ai为超弦的不同的振动的模式时，(i)，(7)，(8)，(25)和(26)式可以用来描述不同弦间的反应，即用来作为判断不同弦间连接和断裂反应过程中所对应物理量的量子数是否守恒，从而可以用来作为判断它们的反应能否发生的判据.

有关因果代数的更多的应用，以及考虑互逆可消条件(3)式不具有互逆元素次序的出现先后无关的对称，这时可定义具有左右不同单位元的新代数系统，并且这新的代数可用于代数拓扑和超弦场论的拓扑等的研究和应用，因为这次序和超弦的等价类的区分相关［22］，限于篇幅，将另文讨论.

6.讨 论

现进一步讨论因果代数的特性，我们先给出群公理的简化.

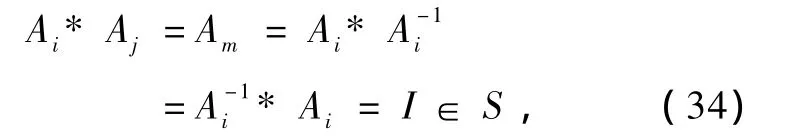
可见事实上单位元定理(ⅲ)的导出是满足封闭性的结果.故由单位元(34)式可知单位元定理(ⅲ)可不作为公理专门提出.所以，现在可以把通常群的公理中单位元除去，因为存在逆元又满足封闭性，必导出存在单位元.可见到目前为止所有的书和论文关于群定义中都有重复的部分.可能有一种观点会认为没有单位元就没法定义逆元，而这样增加定义了单位元，在考虑逆元和封闭性时单位元又可导出，这种重复违反了数学公理最简原则.事实上，利用互逆可消条件可以定义一般的逆元，进一步利用存在消去律，也可导出单位元.因此可直接采用定理(ⅰ)，(ⅳ)和(34)式来定义群.所以，现在群的公理减少了一个，消除了重复定义，而且封闭性(34)式可看作互为逆元定理(ⅱ)所需满足条件的定义，以上讨论揭示了群公理间的内在结构关系.

另一方面，当将定理(ⅳ′)用于Pauli矩阵时，经过计算可得

即Pauli矩阵满足定理(ⅳ′)，这是可直接应用的对称关系.利用逆矩阵的定义计算 Pauli矩阵的逆矩阵，可得，则利用(35)式可得

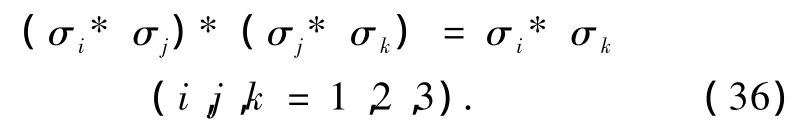
当进一步考虑电子的自旋时，对任意分量的电子自旋角动量，有关系式，将此式代入(35)式，我们得到任意分量电子自旋角动量间的对称关系如下:

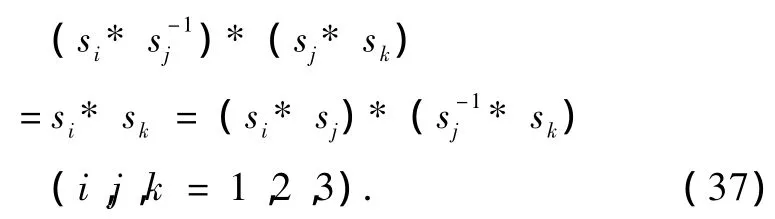
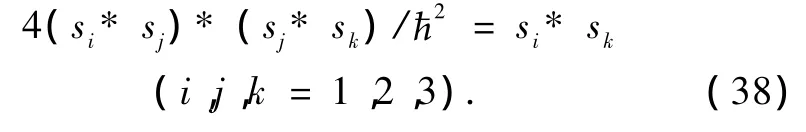
由于这互逆可消条件(3)式具有互逆元素次序的出现先后无关的对称，所以可以导出(35)和(37)式，利用(35)—(38)式，不但可以得到新的对称性，而且可以化简多电子相互作用的计算.

因为由群推不出因果代数，但可推出因果分解代数，又由于本文发现了群具有因果分解代数的性质，那么关于群在粒子物理学中的所有应用［1］，因果分解代数就有对应的应用.

由于加法或乘法分别满足定理(ⅰ)—(ⅳ)条件的集合分别称为加法或乘法群，并且系统在任意严格运算操作过程中必须满足定量因果原理，则由定理(ⅱ)，(34)式和定理(ⅲ)的讨论可见，定理(ⅱ)和(ⅲ)是定量因果原理导出的表达式定理(ⅰ)中元素取特殊值的情况，即不会有凭空的增加或减少的情况，而由定理(ⅰ)，(ⅱ)这两个条件和满足定量因果原理的互逆可消条件定理(ⅳ′)与(ⅳ″)可导出结合律，故定量因果原理把这4个条件有机地统一联系起来了.

本质上讲，一种代数正是满足某些逻辑和定量运算规则的一些元素的一种集合［6，9］，即一种代数正是一些元素的一种集合，这些元素满足某些逻辑运算规则，并且元素的运算满足定量规则，其定量规则正是满足定量因果关系的规则，因为对一个系统而言元素的量运算转换不会凭空的增加或减少，在一处减少多少必定在一处增加多少，也就是满足确定的定量因果关系.如在数学上，(1)式中的D，C，S可以是一个集合中的不同元素，例如可定义为群的元素，群元素的运算满足群的4个定量的逻辑运算规则，而群元素在物理上可有广泛的对应.例如对任意一个物理系统而言，D，C，S可代表该系统的满足群对称操作不变性的所有物理量，如:D，C，S可以是转动不变系统的不同的转动角，空间平移不变系统的不同的平移量.以弦理论为例，D，C，S可以是开弦两端的不同的电荷［21］，以及弦理论中满足不同不变性的群元素［22］.因为群元素正是本文讨论的元素，只是这些元素间满足不同的运算规则就得到不同的代数.如前面已经强调群就是一些元素满足一些群运算规则的一种代数，而半群就是没有关于逆元素的运算规则的一种代数.之所以要研究超出群的一般代数是因为有大量的物理系统没有群的对称性，而有比群更小的对称性.故研究这些更小的对称性就具有重要的物理意义和实用价值.由于本文所研究的代数满足形成不同代数的这些条件，依据现代代数理论［9］，我们的研究不但与现代代数理论自洽，而且可在不同粒子物理系统找到实际的应用［16］.对于具有李群连续对称性的许多物理系统，如文献［23—28］，本文的研究也可给出相关的讨论.故本文的研究不但有理论意义而且有现实的实用价值.

7.结 论

本文不但给出了因果代数，而且还给出了在物理学中的应用.本文依据定量因果原理，给出了一个新的代数系统，并且其公理满足定量因果原理，故称其代数为因果代数，而其余的命题和结论都是其公理的推论.在因果代数中，当进一步在消去律存在下(3)式有解时，因果代数转变为因果分解代数，即，对于因果代数，当满足定量因果原理的互逆可消条件有满足消去律的解时，得到因果分解代数.由因果分解代数导出了结合律和单位元，故因果分解代数又具有群的结构特征，从而进一步给出了这新代数系统在高能物理学中的应用.发现其对称性来源于定量因果原理，一般地给出了在高能粒子反应中，存在大量的类似于(21)或(25)式的反应，得出了因果代数是描述大量真实存在的粒子物理反应的基本工具的结论.得到了给出所有各种相加性、相乘性物理量和不同反应式的具体表示都必须分别满足的统一恒等式，并给出了因果代数和因果分解代数对高能物理的具体应用.特别是当选因果代数的元素Ai为超弦的不同的振动的模式时，定理(ⅰ)，(7)，(8)，(25)和(26)式可以用来作为描述不同的超弦间的反应能否发生的判据，而且超弦理论是统一所有基本相互作用的最有希望的理论，故从以上的讨论可见本文的理论是有一般物理意义的.利用封闭性的表示(25)，可以发现这类反应中，它们有对应于Zk的共同的中间态.还得到了所有各种相加性和相乘性物理量的具体表示都分别必须满足的统一恒等式.利用因果代数的定理(ⅰ)和(ⅳ′)，给出了所有物理量必须满足的恒等式，得到了一个过去不曾得到的关于电子自旋角动量的任意分量间的一个新的对称关系式，利用这新的对称关系式，可以化简多电子相互作用的计算.

利用因果代数的守恒方程(22)和超对称的R数(R=3B+L+2S)，我们得到反应式(23)中相乘性的超对称的PR=(-1)R对称性，即方程(22)的左右两边粒子的超对称 PR的对称性不变，并且可推广到一般的反应.

本文利用定量因果原理，克服了没有单位元就没法定义逆元的困难，利用互逆可消条件定义了一般的逆元.并且得出可直接采用定理(ⅰ)，(ⅳ)和(34)来定义群.所以，现在群的公理减少了一个，消除了重复定义，而且封闭性(34)式也可看作互为逆元定理(ⅱ)所需满足条件的定义，以上讨论揭示了群公理间的内在结构关系.

本文依据定量因果原理不但给出了因果代数，而且给出了因果分解代数，并给出了因果分解代数是与原群公理等价的具有更明晰对称性的新公理系统，有利于对环、群等相关理论的研究和应用.而且因果代数和因果分解代数有不同的数学结构，具有这些代数结构的物理系统非常多.采用定理(ⅰ)，(ⅱ)，(ⅳ′)和(ⅳ″)的因果分解代数与群公理系统等价，可使人们更好地理解因果分解代数和群中的本文所揭示的内禀结构特性，并有利于因果代数和因果分解代数在相关领域的应用等.

感谢李子平和扬安洲教授对本文工作所提出的有益的意见.

［1］Cornwell J A 1984 Group Theory In Physics(Vol.Ⅰ，Ⅱ) (London:Academic Press)

［2］Huang Y C，Lee X G，Shao M X 2006 Mod.Phys.Lett.A 21 1107

［3］Huang Y C，Weng G 2005 Commun.Theor.Phys.44 757

［4］Huang Y C，Lin B L 2002 Phys.Lett.A 299 644

［5］Huang Y C，Yu C X 2007 Phys.Rev.D 75 044011

［6］Xiong Q Y 1994 Modern Algebra(Wuhan:Wuhan University Press)

［7］Sholander M 1959 Am.Math.Month.66 93

［8］Michel S，Single A 1961 Am.Math.Month.68 346

［9］Burris S，Sankappanavar H P 1981 A Course in Universal Algebra (Berlin:Springer-Verlag)

［10］Kobayashi S，Nomizu K 1969 FoundationsofDifferential Geometry(Vol.Ⅰ，Ⅱ.)(Tokyo:Interscience)

［11］Husemoller D 1975 Fibre Bundles(Berlin:Springer-Verlag)

［12］Nash C，Sen S 1983 Topology and Geometry for Physicists (London:Academic Press)

［13］Chern S S 1988 Vector Bundles With a Connection，Studies in Global Differential Geometry， Mathematical Association of America.

［14］Yang S L 1998 Algebra Colloquium 5 459

［15］Xiao J，Yang S L 2001 Algebras and Representation Theory 4 491

［16］Otto Nachtmann 1990 Elementary Particle Physics—Concepts and Phenomena(Translated by A.Lahee and W.Wetzel，Berlin: Springer-Verlag)

［17］Kolb E W，Turner M S 1990 The Early Universe(New York: Addison-Wesley Publishing Company)

［18］Linde A D 1990 Particle Physics and Inflationary Cosmology (Berkshire:Harwood Academic publishers)

［19］Llewellyn Smith C H 1982 Physics Reports 24 1

［20］SergioFerrara1987 Supersymmetry (Amsterdam:Elsevier Science Pub.Co.)

［21］Polchinski J 1998 String Theory，Vol.Ⅰ，Ⅱ (New York: Cambridge University Press);Davies P C W，Brown J 1988 Superstrings(Cambridge:Cambridge University Press)

［22］Green M B，Schwarz J H，Witten E 1988 Superstring Theory (Cambridge:Cambridge University Press)

［23］Dong W S，Huang B X 2010 Acta Phys.Sin.59 1(in Chinese)［董文山、黄宝歆2010物理学报59 1］

［24］Jia L Q，Cui J C，Zhang Y Y，Luo S K 2009 Acta Phys.Sin.58 16(in Chinese)［崔金超、贾利群、罗绍凯、张耀宇2009物理学报58 16］

［25］Fang J H，Liu Y K 2008 Acta Phys.Sin.57 6699(in Chinese)［方建会、刘仰魁2008物理学报57 6699］

［26］Wang C，Zhang K，Zhou L B 2008 Acta Phys.Sin.57 6718(in Chinese)［王 策、张 凯、周利斌2008物理学报57 6718］

［27］Zhang Y 2009 Chin.Phys.B 18 4636

［28］Lin P，Fang J，Pang T 2008 Chin.Phys.B 17 4361

PACS:02.10.De，02.20.-a，13.30.-a

Causal algebra and its applications to physics*

Huang Yong-ChangHe Bin1)2)Huang Chang-Yu3)Yang Shi-Lin2)Song Jia-Min1)
1)(Institute of Theoretical Physics，Beijing University of Technology，Beijing 100124，China)
2)(Institute of Applied Mathematics，Beijing University of Technology，Beijing 100124，China)
3)(College of Physics，Peking University，Beijing 100871，China)

2 February 2009;revised manuscript

18 May 2010)

A causal algebra and its application to high energy physics is proposed.Firstly on the basis of quantitative causal principle，we propose both a causal algebra and a causal decomposition algebra.Using the causal decomposition algebra，the associative law and the identity are deduced，and it is inferred that the causal decomposition algebra naturally contains the structures of group.Furthermore，the applications of the new algebraic systems are given in high energy physics.We find that the reactions of particles of high energy belonging neither to the group nor to the ring，and the causal algebra and the causal decomposition algebra are rigorous tools exactly describing real reactions of particle physics.A general unified expression(with multiplicative or additive property)of different quantities of interactions between different particles is obtained.Using the representation of the causal algebra and supersymmetric R number，the supersymmetric PR=(-1)Rinvariance of multiplying property in the reactions of containing supersymmetric particles is obtained.Furthermore，a symmetric relation between any components of electronic spin is obtained，with the help of which one can simplify the calculation of interactions of many electrons.The reciprocal eliminable condition to define general inverse elements is used，which may renew the definition of the group and make the number of axioms of group reduced to three by eliminating a superabundant definition.

symmetry，group theory，causal principle，particle physics

*国家自然科学基金(批准号:10875009，11072007)和北京市自然科学基金(批准号:1072005，1082002)资助的课题.

*Project supported by the National Natural Science Foundation of China(Grant Nos.10875009，11072007)and the Natural Science Foundation of Beijing，China(Grant Nos.1072005，1082002).