李群峰

（河南师范大学 经济与管理学院，河南新乡 453007）

0 引言

作为一种精确地描述自变量对于因变量的变化范围以及条件分布影响的统计方法，分位数回归的概念最早由Koenker和Bassett（1978）［1］提出。借助Laplace（1818）提出的最小绝对残差估计思想，他们针对最小二乘回归的某些缺陷，创建了线性分位数回归理论。Bassett(1986)［2］、Powell(1986)［3］和 Chernozhuko(2002)［4］等人在此基础上进行了深入的研究，陆续解决了分位数回归的线性假设检验、异方差的稳健性检验、估计量的一致性和线性规划解法等应用方面的难题，使其成为了近几十年来发展较快、应用广泛的回归模型方法。和最小二乘方法相比，分位数回归放宽了对被解释变量分布假设的限制，采用加权残差绝对值之和的方法估计参数，应用的条件更为宽松，挖掘的信息更丰富，存在以下优势：（1）分位数回归对模型中的随机误差项不需做任何分布的假定，对残差分布的限制大为减少，当误差呈现非正态分布时，其参数估计量比最小二乘法更有效；（2）分位数回归法通过测度回归变量在不同分位数水平下的参数估计值，突出了局部之间的相关关系，能更加全面的刻画分布的特征；（3）和最小二乘方法通过误差平方和最小进行参数估计不同，分位数回归通过加权残差绝对值之和最小来得到参数估计量，因而对于异常值的敏感程度也远远小于最小二乘方法，从而其参数估计量更为稳健;（4）在回归系数的解释效果方面，最小二乘回归反映的是自变量对因变量影响的平均边际效果，而分位数回归则是自变量对因变量在某个特定分位数水平上影响的边际效果。分位数回归可以提供不同分位点处的估计结果，因此可以对因变量的整个分配情况作出更为清楚的阐释。

面板数据作为截面数据与时间序列数据综合起来的二维数据类型，在经济生活中有着极其广泛的应用。将分位数回归和面板数据模型结合对变量之间的关系进行分析，可以充分利用面板数据的特点，更好地识别和度量纯时间序列和纯横截面数据所不能发现的影响因素。同时面板数据分位数回归还可以测度自变量对因变量的某个特定分位数的边际效果，更好地在控制个体异质性的基础上分析因变量条件分布的不同分位点上变量之间的关系。

1 分位数回归的基本原理

从理论上讲，分位数回归是对以古典条件均值模型为基础的最小二乘法的拓展。由于其采用多个分位函数对整体模型进行估计，因而可以测度自变量对因变量每个特定分位数的边际影响。对一个连续随机变量y，如果y小于等于qτ的概率是τ，则我们说y的τ分位值是qτ，或者说qτ就称作y的第τ分位数。这也就是说，对于F(y)=prob(Y≤y)，可得

类似地，如果我们将被解释变量y表示为一系列解释变量X的线性表达式，并使得该表达式满足小于等于qτ的概率是τ，就称为分位数回归。

分位数回归的参数估计原理实际上是使一个关于y与其拟和值之差绝对值的表达式最小，即加权绝对残差最小(WLA)。考虑一般模型

其中，τ为估计中所取的各分位点，βτ为各分位点斜率系数的估计值，ατ为各分位点截距项的估计值。其分位数回归的基本思想是对于在回归线上方的点(残差为正），赋予其权重为τ，对于在回归线下方的点(残差为负)，赋予其权重为(1-τ)，然后求误差绝对值的加权和。分位数回归的参数估计量的求解则是要在加权残差绝对值之和最小化的条件下计算参数α和β的值。中位数回归是分位数回归的特殊情况，在加权残差绝对值之和中采用对称权重，而其他的条件分位数回归则使用非对称权重。

在参数估计量的求解上，分位数回归要比传统的最小二乘回归复杂得多。传统的最小二乘回归是使得被解释变量y与其拟合值之差的平方和最小，而分位数回归是使得这个残差的加权绝对值的一个表达式最小，并且这个表达式不可微，因此传统的求导方法不再适用，而只能采取线性规划法（LP）估计其最小加权绝对偏差，从而得到解释变量的回归系数。目前较为流行的算法有三种，即单纯形算法、内点算法和平滑算法等。这些计算方法基本上都是通过迭代求解。现在大部分统计计算软件SAS、STATA、EViews、MATLAB等中都具有分位数回归功能。

2 分位数回归方法与面板数据模型

面板数据分位数回归是对面板数据模型采用分位数回归的方法进行参数估计。通过将分位数回归和面板数据模型相结合对变量之间的关系进行研究，可以更好地在控制个体差异的基础上对因变量条件分布的不同分位点上各种变量之间的关系进行分析。面板数据模型可以分为混合估计模型、固定效应模型和随机效应模型三类。混合估计模型因为在不同时间和截面上均不存在显著差异，可以视为普通最小二乘模型。随机效应模型因为误差项在时间和截面上均具有相关性，一般采用广义最小二乘估计。固定效应模型由于对于不同的截面或不同的时间序列，模型的截距是不同的，则可以采用在模型中加虚拟变量的方法通过分位数回归得到参数估计量。我们以固定效应情形为例，进行面板数据模型的分位数回归，并对分位数回归和最小二乘回归的优劣加以比较。

考虑以板数据模型：

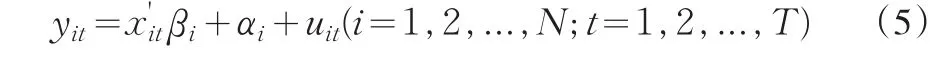
当τ在(0,1)上变动时，求解加权绝对残差最小化问题就可以得到分位数回归在不同分位点上的参数估计量。最小化加权绝对残差的表达式为

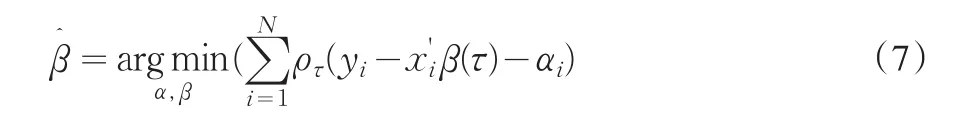
其中，i代表不同的样本个体，t代表不同的样本观察时点，u表示随机误差项向量，βi表示解释变量的系数向量，αi表示不同样本不可观察的随机效应向量。

如果采取分位数回归方法对于上述面板数据模型进行参数估计，则首先需要建立条件分位数方程

如果不用向量表示，则可以表示为

其中，ρτj为与各分位数相对应的权重。

利用Eviews6.0软件的分位数回归功能通过迭代求解，可以很方便的对以上面板数据模型求出因变量在不同分位点水平上对应的参数估计量。

3 应用实例

分位数回归方法对于因变量的某些非标准分布下回归方程的系数估计有较好的效果。基于这个特点，在对变量之间的关系进行分析时，采用面板数据模型进行分位数回归可以使各参数估计显著程度更高，回归分析结果更加稳健。本文在对比最小二乘法与分位数回归方法在面板数据模型中的估计效果时，以1998～2006年25个行业企业销售收入为因变量，专利申请数量为自变量，分析企业研发能力和销售收入之间的关系，分别采取最小二乘法和分位数回归法进行参数估计和比较分析。为了简便起见，本文仅仅对混合估计模型和固定效应模型的估计结果进行比较分析（表1）。

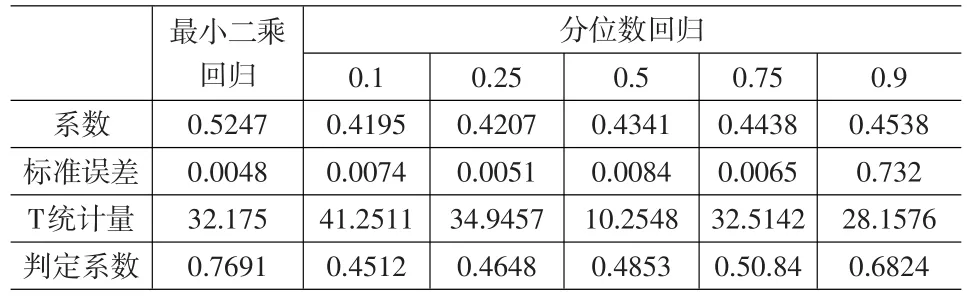
表1 最小二乘法与分位数回归结果比较（固定效应模型）

面板数据分位数回归能够估计因变量在给定自变量下在各个分位点上的条件分布。从回归结果中可以看出，分位数回归得到的系数符号和最小二乘回归基本相似，但是随着企业销售收入在条件分布的不同位置而发生变动，呈现出一定的变化趋势。从结果看，专利申请量的系数在所考察分位点的值随着条件分布由低端向高端变动时，系数逐渐开始增大。如在0.1低分位点处系数值为0.4195，在0.5分位点处为0.4341，而在0.9分位点处为0.4538。其经济意义为：当企业销售收入的条件分布位于0.9分位点处时，专利申请量的促进作用最为显著；而在其他分位点水平上，专利申请量的促进作用则相对较弱。在不同分位点位置上，专利申请数量的影响表现出一定的变化规律，这是最小二乘回归模型所无法反映的信息。此外，在同一情形下做回归分析，显然分位数回归分析结果更加稳健，各系数显著性更强。因而，面板数据模型的分位数回归估计在实际应用中可以发挥重要作用。

4 结论

本文在对分位数回归方法的基本原理进行全面分析说明的基础上，对其在面板数据模型中的应用作了深入分析，并对不同回归估计方法在面板数据模型中的估计效果进行了比较分析。结果表明，在对变量之间的关系进行分析时，面板数据模型的分位数回归除了可以测度自变量对因变量的某个特定分位数的边际效果外，还可以使各参数估计量显著程度更高，回归分析结果更加稳定和精确。

[1]Koenker,Bassett.Regression Quantiles[J].Econometrica,1978,(46).

[2]Bassett,Koenker.Strong Consistency of Regression Quantiles and Related Empirical Processes[J].Econometric Theory,1986,(2).

[3]Powell,James L.Censored Regression Quantiles[J].Journal of Econometrics,1986,(32).

[4]Hong H,Chernozhukov V.Three-Step Censored Quantile Regression and Extramarital Affairs[J].Journal of the American Statistical Association,2002,(97).