刘缵武，刘世晗，黄 欧

1.信息工程大学理学院，河南郑州450001；2.郑州市市政工程总公司，河南郑州450007；3.美国俄亥俄州立大学地球科学学院，俄亥俄哥伦布43210

1 引 言

由于当今卫星跟踪技术、卫星测高以及重力场求解技术的发展，国内外正在把高阶次重力场模型向更高阶次扩展［1－5］。显然，超高阶次球谐位系数模型的构制与应用，与超高阶次缔合勒让德函数及其导数的计算密切相关。并且，随着航天技术的不断发展，需要构建的位系数模型的阶次越来越高。因此，研究计算超高阶次缔合勒让德函数及其导数值的方法是非常必要的［4，6－7］。

由缔合勒让德函数及其关于θ的导数构成的球谐级数表达式为

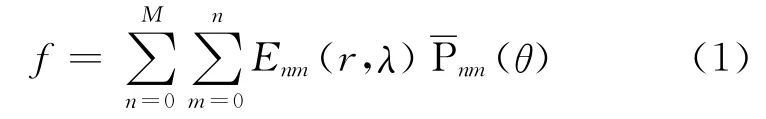
和

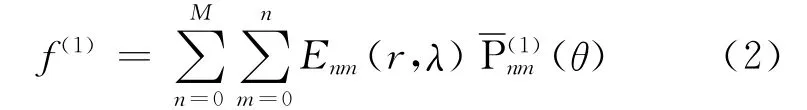
式中，（r，θ，λ）是空间点的球面坐标，r是点至地心的距离，θ是地心余维，λ是经度；M是球谐展开式的最大阶数；Enm（r，λ）是与阶n和次m有关的（r，λ）的函数；和是n阶m次第一类完全正常化缔合勒让德函数和它们的导数。

例如，在点（r，θ，λ）处，地球外部扰动位T（r，θ，λ）的M阶球谐级数表达式为［8］

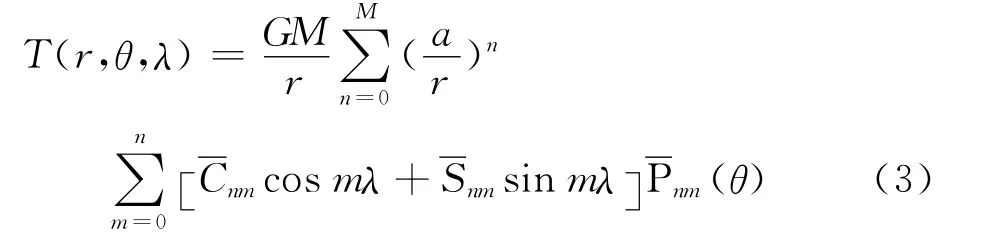
这里

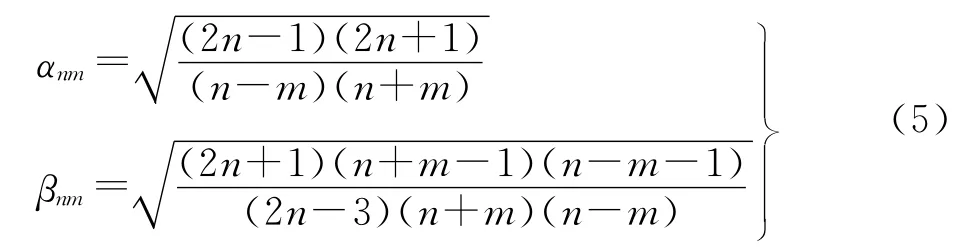
式中，

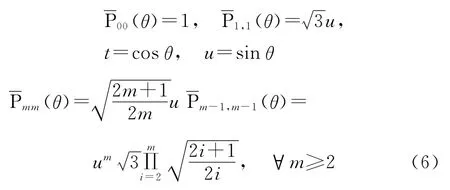
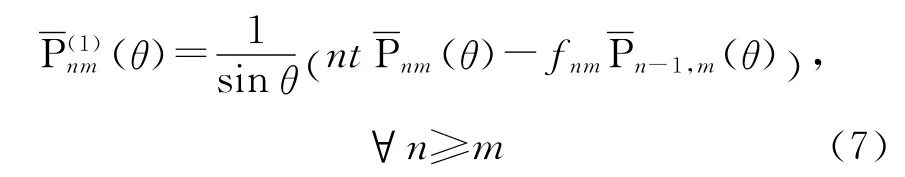
式中

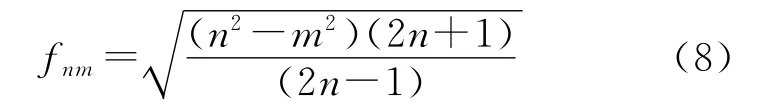
按式（4）～式（8）递推计算，当M＝2 500在接近两极时函数值达到10－4000量级［4，6］。而一般个人计算机的允许数值范围约在10－310和10＋310之间［10］。为了避免下溢，文献［4］修改递推式（4）和式（7）为

计算式（1）采用如下Horner求和技术［4，12］

式中，

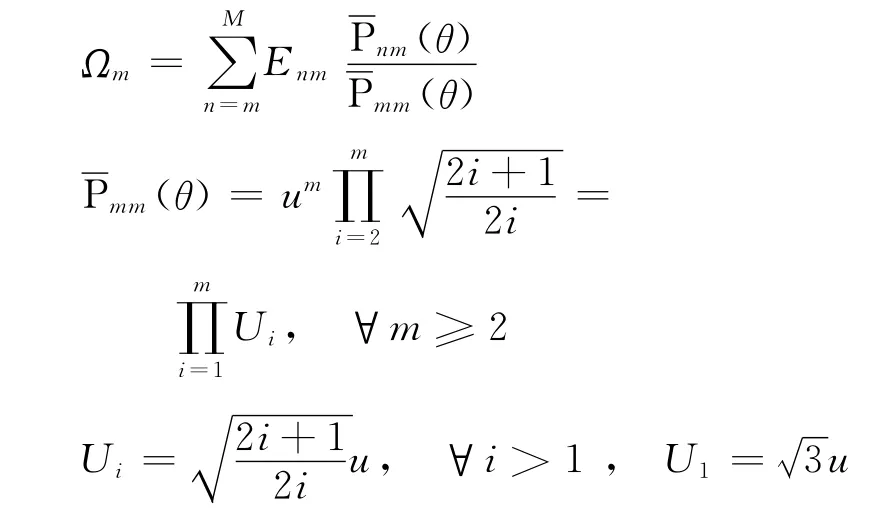
式（2）可以类似计算。

的值当M＝2 700，θ→0°时将超过10500。为了避免上溢，递推过程中乘以一个下调因子［4］10－280。

2 递推计算中的压缩因子和复合Horner求和技术

分析式（9）中的系数因子t、αnm和βnm不难发现，对确定的θ和m，当n很大时，βnm接近于1；当θ→0°时t→1，且它不随m和n的变化而变化；而随着n的增大αnm趋于2（对于固定的m），且当m＜n＜1.666 7 m时αnm＞2.5。因此，每一列递推，n由m增大到n＝1.666 7 m，每一步递推值将增大超过αnm／βnm＝1.5倍。例如，当n由m＝ 2 700增大到n＝1.666 7 m（约4 500）时，如果不顾及t的微小影响，递推值将远远超过初始值的9×10316（实际超过1×10500）倍以上。

鉴于以上分析，在递推中插入压缩因子q，式（9）变为

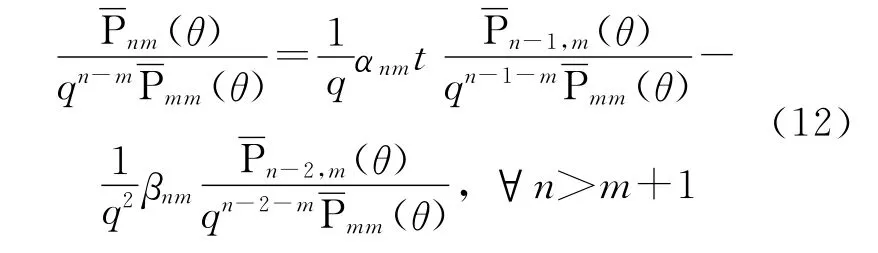
式中，q是与θ有关的介于1和2之间的一个数。显然，与式（9）相比，式（12）降低了递推值增大的速度。

当θ逐渐增大到90°时，t＝cosθ逐渐减小到0，式（9）右端第一项作用越来越小，递推值主要依赖于第二项。为避免下溢，这时取q＝1。由此，定义q为

式中，ρ是一个介于0.5和1之间的常数；k是一个正整数。令

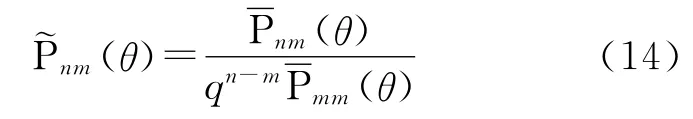
式（12）改写为

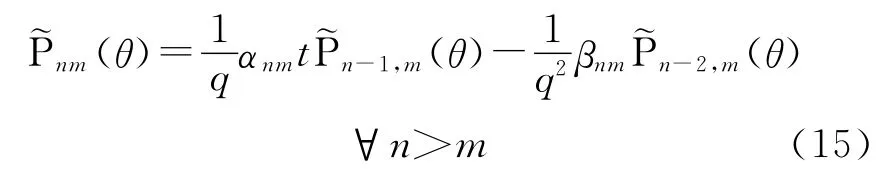
式中，

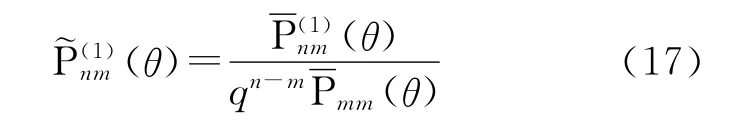
式（1）的值如下计算

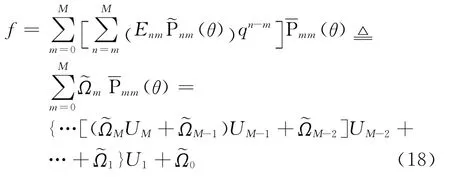
式中，

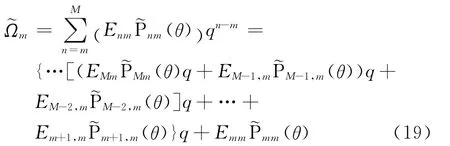
式（18）和式（19）合称为复合Horner求和技术。

式（2）中f（1）可以类似计算。

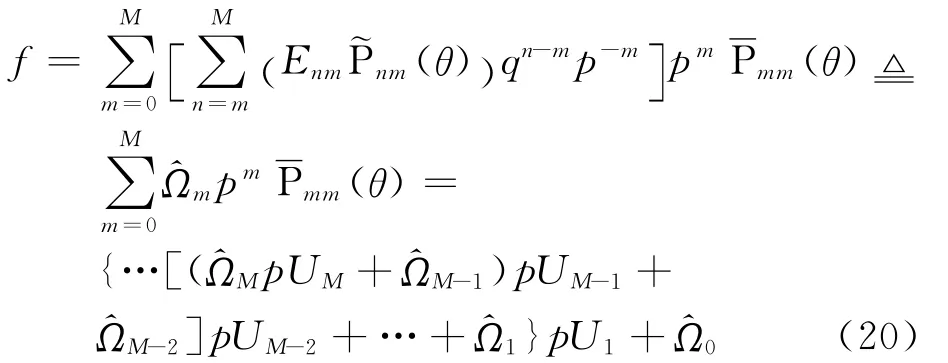
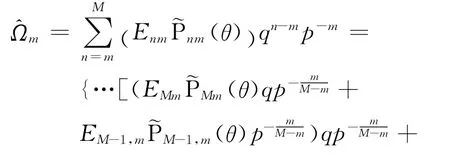
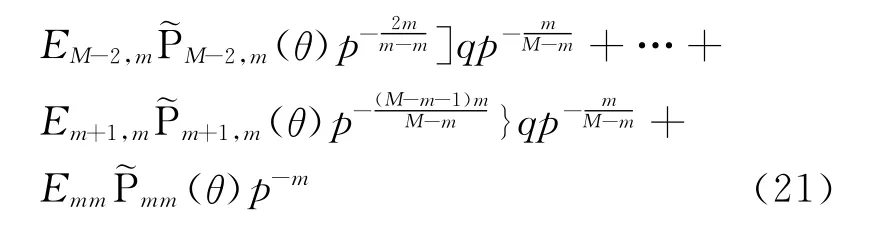
式（20）和式（21）也可合称为复合Horner求和技术。

3 数值检验

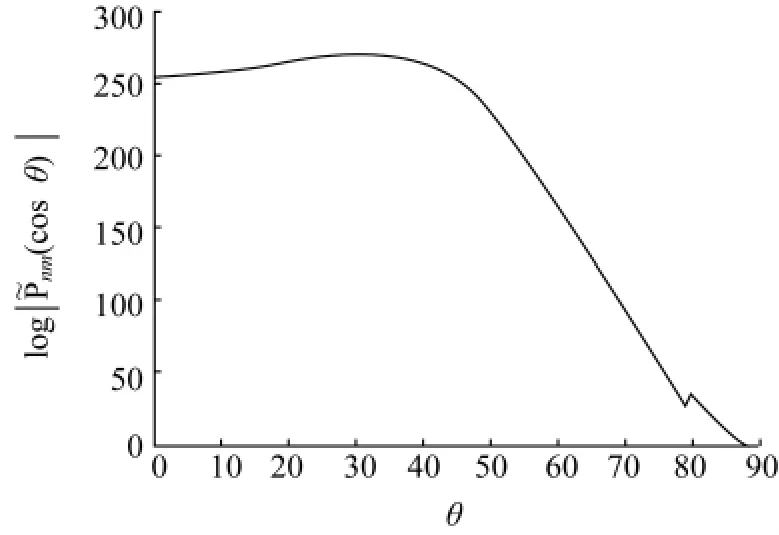
图1 ｜（θ）｜（∀n，m≤3 600）的最大值的对数值曲线Fig.1 Logarithm plot of maximum values of｜（θ）｜（∀n，m≤3 600）

图2 ｜（θ）｜（∀n，m≤3 600）的最小值的对数值曲线Fig.2 Logarithm plot of minimum values of｜（θ）｜（∀n，m≤3 600）

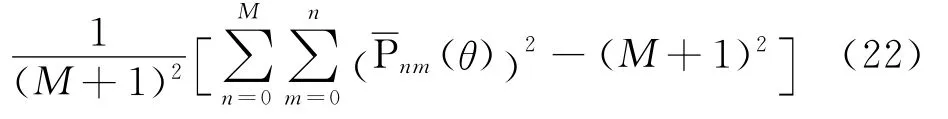
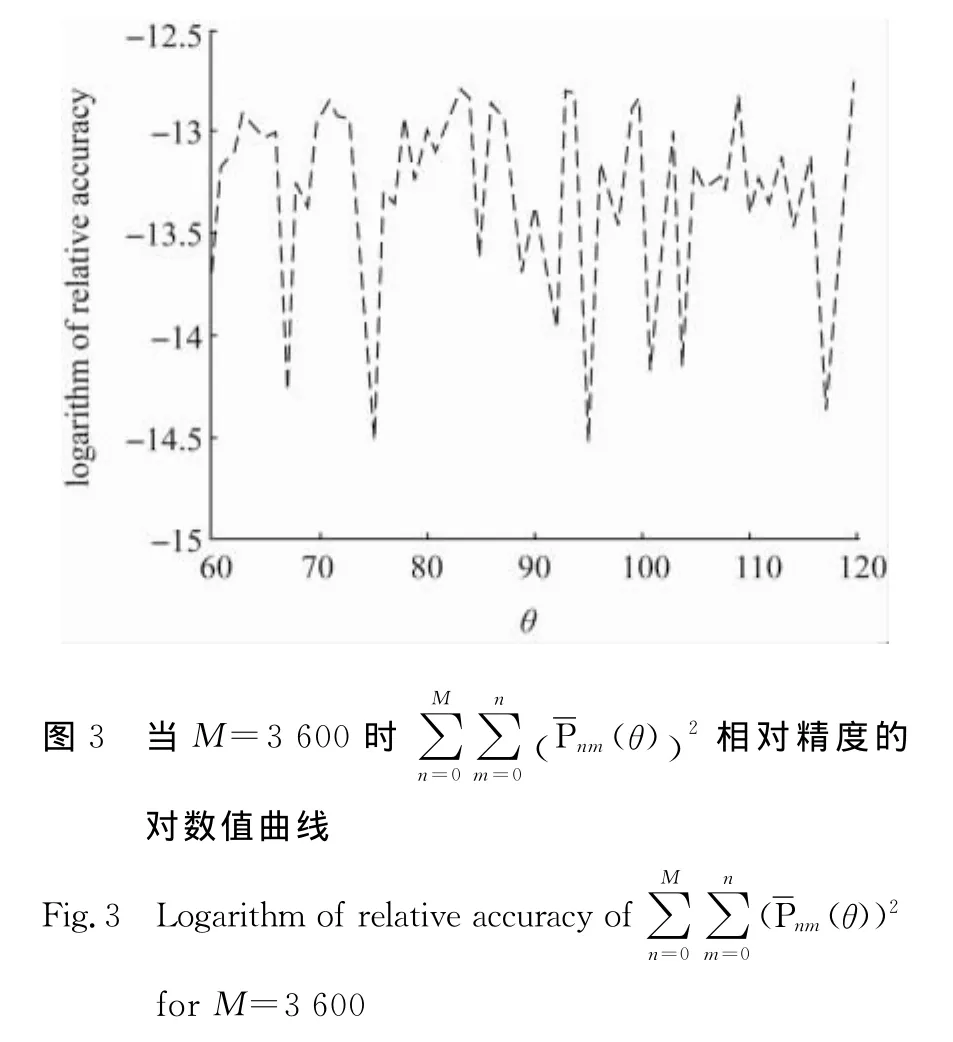
式中，

式（23）、式（24）类似于式（20）、式（21）计算。

从图3看到，新算法求得的完全正则化缔合勒让德函数值具有较高的精度，同时图1～图3也说明新算法有较好的稳定性。

Belikov递推法的计算公式为

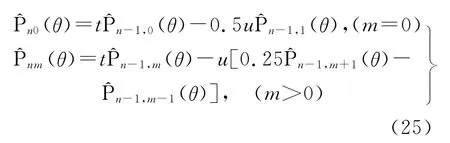
式中，

跨阶次递推法的计算公式为

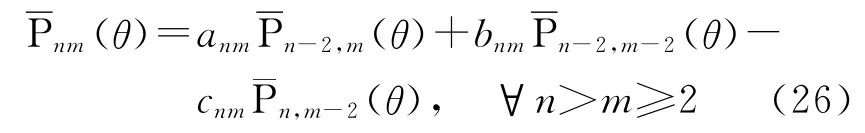
式中，

由于式（25）和式（26）的递推系数都小于1，因此比式（4）的稳定性要强。但在接近两极时的值仍然达到10－4000量级，超出一般计算机的允许数值范围而下溢。根据式（25）和式（26）的结构，不能像式（9）那样处理。不过，式（25）可改写为

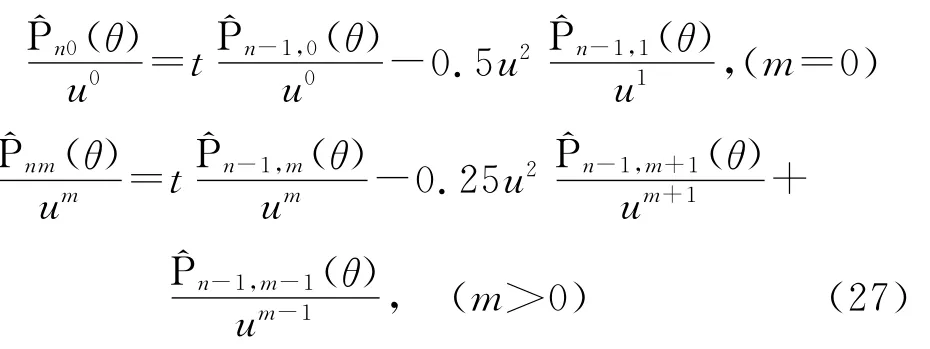
由式（27）计算＾Pnm（θ）／um可避免下溢，且若递推中乘以10－280，可计算至2 500阶不会上溢。由此转化为就可类似式（11）计算式（1）。但当M＞2 500时出现上溢，若要进一步提高计算的阶次，因＾Pnm（θ）／um由三项构成，则压缩因子结构非常复杂。

跨阶次递推式（26）若如法处理，则产生系数βnm／u2和γnm／u2，当θ→0°它们急剧变大，虽然避免了下溢，但很快出现上溢。由此分析，利用本文的处理思想，当阶次很高时，无法避免递推值的溢出。

4 结 论

在个人计算机上执行现有的递推公式计算超过M＞2 700阶次的缔合勒让德函数会产生上溢或下溢。通过在基本递推算法中插入压缩因子法，避免了溢出现象的发生。同时给出了计算由完全正则化缔合勒让德函数构成的超高阶球谐级数式的复合Horner求和技术。数值检验表明新算法具有较高的精度。

毫无疑问，在大地测量中会有包含真实扰动位系数在内的计算缔合勒让德函数级数f的更严密的检测方法。本文重点在于提出缔合勒让德函数递推的压缩因子算法和复合Horner求和技术的思想。依据这个思路，Belikov递推法可以类似处理，且递推计算更高阶的缔合勒让德函数级数及确定相应的级数求和技术，都会涉及更为复杂的压缩因子和球谐级数求和手段；任意高阶的缔合勒让德函数递推算法及其相应的级数求和问题，必须要有新的思想和方法；跨阶次递推法很难利用本文给出的方法处理下溢问题。对以上问题，将进一步研究。

［1］ WENZEL G.Ultra－high Degree Geopotential Models GPM98A，B，and C to Degree 1 800［C］∥Joint Meeting of the International Gravity Commission and International Geoid Commission.Trieste：［s.n.］，1998.

［2］ LIU Zuanwu，LU Zhonglian.A Study of Incomplete Geopotential Coefficient Model［J］.Geophysics，1998，41（1）：89－98.

［3］ HUANG Motao，ZHAI Guojun，OUYANG Yongzhong，et al.Analysis and Computation of Ultra High Degree Geopotential Model［J］.Acta Geotaetica et Cartographica Sinica，2001，30（3）：208－213.（黄漠涛，翟国君，欧阳永忠，等.超高阶地球位模型的计算与分析［J］.测绘学报，2001，30（3）：208－213.）

［4］ HOLMES S A，FEATHERSTONE W E.A Unified Approach to the Clenshaw Summation and the Recursive Computation of Very High Degree and Order Normalised Associated Legendre Functions［J］.Journal of Geodesy， 2002，76（5）：279－299.

［5］ PAVLIS N K，HOLMES S A，KENYON S C，et al.Earth Gravitational Model 2008（EGM2008）－WGS－84Version［EB／OL］.［2010－02－20］.http：∥earth－info.nga.mil／GandG／WGS－84／gravitymod／egm2008／index.html.

［6］ JEKELI C，LEE J K，KWON J H.On the Computation and Approximation of Ultra－high Degree Spherical Harmonic Seies［J］.Journal of Geodesy，2007，81（9）：603－615.

［7］ WANG Jianqiang，ZHAO Guoqiang，ZHU Guangbin.Contrastive Analysis of Common Computing Methods of Ultra－high Degree and Order Fully Normalized Associated Legendre Function［J］.Journal of Geodesy and Geodynamics，2009，29（2）：126－130.（王建强，赵国强，朱广彬.常用超高阶次缔合勒让德函数计算方法对比分析［J］.大地测量与地球动力学，2009，29（2）：126－130.）

［8］ HEISKANEN W A，MOTITZ H.Physical Geodesy［M］.San Francisco：Freeman，1967.

［9］ COLOMBO C.Numerical Methods for Harmonic Analysis on the Sphere：Rep 310［R］.Columbus：Ohio State University，1981.

［10］ OVERTON M L.Numerical Computing with IEEE Floating Point Arithmetic［M］.Philadelphia：SIAM，2001.

［11］ KOOP R，SPTELPSTRA D.On the Computation of the Gravitational and Its First and Second Order Derivatives［J］.Manuscripta Geodaetica，1989（14）：373－382.

［12］ GLEASON D M.Partial Sums of Legendre Series via Clenshaw Summation［J］.Manuscr Geod，1985（10）：115－130.