Duffing单边碰撞系统的颤振分岔*
2010-09-19冯进钤牛玉俊
冯进钤 徐 伟 牛玉俊
1)(西北工业大学理学院应用数学系,西安 710072)
2)(西安工程大学理学院,西安 170048)
Duffing单边碰撞系统的颤振分岔*
冯进钤1)2)†徐 伟1)牛玉俊1)
1)(西北工业大学理学院应用数学系,西安 710072)
2)(西安工程大学理学院,西安 170048)
(2009年3月27日收到;2009年4月26日收到修改稿)
针对碰撞系统中常见的颤振导致的彗尾碰撞问题,引入了彗尾映射的概念,提出了一种有效的研究碰撞系统中颤振现象的数值方法.并以典型的Duffing单边碰撞系统为例,研究了系统中的完全颤振和不完全颤振现象,同时分析了系统的颤振分岔.
Duffing碰撞系统,彗尾映射,颤振分岔
PACC:0547
1.引言
非光滑动力系统作为动力学的一个分支,广泛的存在于多个科学领域.近年来,关于非光滑系统动力学的研究引起了大量学者的关注[1—4].早期, Shaw,Holmes[5]研究了一个周期激励的线性碰撞系统的混沌.随后非光滑系统的研究掀起了一股热潮,也取得了许多的成果,主要包括Brogliato[6], Kunze[7],Leine和Nijmeijer[8],金栋平和胡海岩[9], Bernardo等[10]专著.
非光滑系统中通常存在擦边和颤振这两种新颖的动力学特性,使得非光滑系统呈现出许多光滑系统中所没有的复杂动力学行为,主要有非光滑分岔[11],碰撞系统中的颤振动力学[12].Alzate[13]分析了一个齿轮装置的颤振现象.本文以一般的碰撞系统为模型,通过引入一个彗尾映射,有效的近似完全颤振中产生的彗尾碰撞.并以一个典型的Duffing单边碰撞系统为例,分析了该系统中的两类颤振分岔及其发生的机理.
2.彗尾映射
考虑一般的碰撞系统,其系统自由运动方程如下:

这里下标“-”和“+”分别表示碰撞前后时刻.映射R表示碰撞法则,通常可以表示为
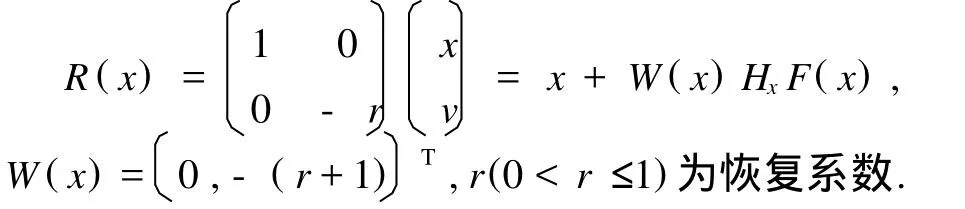
为了描述方便,引入约束面如下:

设自由运动时系统(1)第一式的轨线流为Φ(x,t),则系统轨线沿约束面Σ法线方向的速度和加速度分别为

在一定条件下,系统(1)除了自由运动和高速碰撞外,还可能紧贴约束面Σ,产生黏滑运动.由文献[10],定义黏滑面如下:

当x∈ΣS时,对应的黏滑运动方程为

事实上,黏滑运动与系统的颤振有着紧密的关系.颤振通常包括完全颤振和不完全颤振.所谓完全颤振表示在有限时间间隔内系统发生了无穷次的碰撞;不完全颤振表示有限时间间隔内系统发生N(N为一个很大的有限数)次碰撞.
文献[13]告诉我们,系统黏滑运动通常经历一个从完全颤振到黏滑,再到逃离黏滑面的过程,完全颤振的结束点即为黏滑运动的开始点.对于完全颤振,从无穷次的碰撞到完全碰撞结束的过程中会产生所谓的“彗尾”碰撞,占用大量的计算资源.为了避免这种彗尾碰撞问题,我们引入一个彗尾映射.首先,我们定义一个完全颤振子空间

如图1,取完全颤振子空间中的初始点x0∈ΣC,先经过碰撞映射R(x)到达x01,再自由运动到下一个碰撞点x1,如此无穷次碰撞后,最终到达完全颤振的结束点x*,其满足

我们定义彗尾映射为S,

令

由于0<ε≪1,利用幂级数的展开,我们得到

其中T表示系统从状态x01运动到状态x1的时间.在完全颤振子空间中,系统从状态x01到状态x1的过程中,系统的法向速度必在某xv处改变符号,从而

得到近似时间

代入(9),(10)式,同时利用x01=R(x0),整理得到


图1 彗尾映射示意图
进一步,(12),(13)式可改写为

其中

考虑到

由(14)式递推整理得
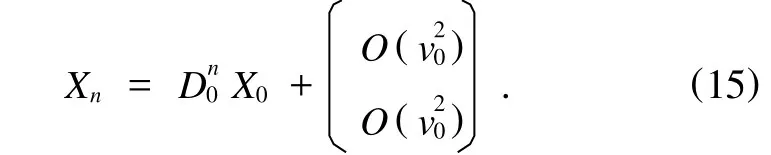
由线性代数知识,矩阵D0的特征值为1和r,存在相似变换矩阵P,使得

进而得到

将(17)式代入(15)式,整理得



在(19)式中,我们定义一阶修正项为

3.Duffing单边碰撞系统的颤振分析
考察一个典型的Duffing单边碰撞系统,系统描述如下:


令x=(x1,x2,x3),对比(1)式有

对应的法向速度和加速度分别为

当固定系统参数α1=-1,α2=1,β=0.2,f= 1.5,ω=0.2,Δ=1,r=0.8,完全颤振子空间(7)式中取ε=10-8,初始条件为(0.8,-0.2,0)T,图2(a)表示P(∞,1)运动(这里符号P(m,n)表示n个周期中发生m次碰撞),时间历程图(图2(b))给出了从完全颤振到黏滑的过程,图2(b)的局部放大(图2 (c),(d))呈现了完全颤振中的彗尾映射S:xC→xS1.其中彗尾开始点为

图2 系统(22)式的完全颤振到黏滑运动的彗尾映射 (a)相图(符号■表示Poincaré映射点);(b)时间历程图(实线为x2关于t变化曲线,虚线为x1关于t变化曲线,xS1和xS2分别表示黏滑开始点和结束点);(c),(d)为(b)的局部放大(对应(19)式中x0=xC,x*=xS1)

由(19)—(21)式求得完全颤振结束点(即为黏滑开始点)为

彗尾时间和修正项分别为
t*=7.18×10-10,

可见,彗尾映射不仅保证了较高的数值精度,同时有效地避免了数值计算中的“彗尾”问题.
3.1.完全颤振到不完全颤振分岔

图3 频闪分岔图 (a)x1随r变化;(b)x2随r变化
当系统的其他参数与图2一样,考察恢复系数对系统的颤振的影响.图3给出了系统状态关于恢复系数r的频闪分岔图.从图3可以看到,当r 从系统的时间历程图来看,当r=0.873 图4 时间历程图 (a)r=0.873;(b)r=0.874 为了更清晰的呈现这种分岔现象,图5给出了黏滑时间τ(图2中状态xS1到状态xS2的时间)关于分岔参数r的变化图.当r 图5 黏滑时间关于恢复系数r的变化图 从图3,我们看到,当增大恢复系数到r>rⅠ时,系统表现为不完全颤振的周期1运动.但是,其Poincare映射不动点不再随分岔参数r连续的变化,而是呈现出间断的不连续性.随着参数r的继续增大,系统出现了逐渐增大的具有自相似结构的不连续窗口,在这些不连续窗口中,我们可以清楚地看到从周期1运动突然变为拟周期运动的分岔现象.为了分析这种突然的跃迁,我们选择图3中rⅡ≈0.89210附近进行研究.当参数r=0.89209 图6 Poincare截面图和时间历程图 (a)r=0.89209,Poincare截面图;(b)r=0.89209,时间历程图;(c)r=0.89210,Poincare截面图;(d)r=0.89210,时间历程图 图7 最小碰撞时间间隔与参数r的关系 为了更进一步研究图3中出现的逐步增大的结构,我们给出了每两次碰撞之间的最小时间间隔Δ τ关于参数r的变化关系,见图7.当存在黏滑运动时,我们定义Δ τ=0.图7告诉我们,Δ τ从零变为非零值对应系统从完全颤振到不完全颤振的转折点.随着r的增大,Δ τ也不断的增大,说明系统在逐渐的远离颤振运动.此外,我们发现,Δ τ并不是随着r连续变化的,存在一系列的不连续点,随着r的越大,这种间断的不连续性也呈现出逐步放大的自相似结构,实际上这与图3中的自相似不连续窗口是一致的.这也表明,在不完全颤振中,系统颤振越剧烈,对分岔参数更加敏感. 在一定条件下,碰撞系统中通常存在由于完全颤振导致的彗尾碰撞问题,不仅占用大量的计算资源,而且使得一般的数值积分方法失效.为此,本文借助一种彗尾映射,在指定精度下给出了一种有效的近似.同时,以一个典型的Duffing单边碰撞系统为例,我们对该系统中的颤振进行了分析.研究表明,系统存在两种常见的包含颤振的分岔:一种为完全颤振到不完全颤振的分岔,这种分岔是以黏滑过程的突然产生或消失作为标准;另一种为不完全颤振中的周期运动到拟周期运动的分岔,这种分岔是由于不完全颤振的末端碰撞轨不断的发生擦边引起的,形成了一种自相似的逐渐放大的分岔结构.同时,通过考察最小碰撞时间间隔,我们发现,系统颤振越剧烈,对分岔参数越敏感.可见,颤振分岔是非光滑系统中所特有的分岔,具有许多光滑系统中分岔所没有的特性.本文的研究适用于一般的碰撞系统,包括线性碰撞系统,弱或强非线性碰撞系统的颤振研究,为更进一步的理论分析提供有效的指导. [1]Niu YJ,Xu W,Rong H W,Wang L,Feng J Q 2008Acta Phys. Sin.57 7535(in Chinese)[牛玉俊、徐 伟、戎海武、王 亮、冯进钤2008物理学报57 7535] [2]Feng J Q,Xu W,Wang R 2006Acta Phys.Sin.55 5733(in Chinese)[冯进钤、徐 伟、王 蕊2006物理学报55 5733] [3]Li GJ,Xu W,WangL,FengJ Q 2008Acta Phys.Sin.57 2107(in Chinese)[李高杰、徐 伟、王 亮、冯进钤2008物理学报57 2107] [4]Li M,Ma X K,Dai D,Zhang H 2005Acta Phys.Sin.54 1084(in Chinese)[李 明、马西奎、戴 栋、张 浩2005物理学报54 1084] [5]Shaw S W,Holmes PJ 1983Phys.Rev.Lett.51 623 [6]Brogliato B 1999Nonsmooth Mechanics:Models,Dynamics and Control(London:Springer-Verlag) [7]Kunze M 2000Non-Smooth Dynamical Systems(Berlin:Springer) [8]Leine R I,Nijmeijer H 2004Dynamics and Bifurcations in Non-Smooth Mechanical Systems(Berlin:Springer) [9]Jin D P,Hu H Y2005Vibration and Control of collision(Beijing: Science Press)(in Chinese)[金栋平、胡海岩2005碰撞振动与控制(北京:科学出版社)] [10]di Bernardo M,Budd C,Champneys A R,K owalczyk P 2007 Piecewise-smoothDynamicalSystems:TheoryandApplications (London:Springer-Verlag) [11]di Bernardo M,Budd C,Champneys A R,K owalczyk P,Nordmark A B,Olivar G,Piiroinen P T 2008SIAM Review50 629 [12]Budd C,Dux F 1992The dynamics of impact oscillators(Bristol:Ph. D.thesis,University of Bristol) [13]Alzate R 2008Analysis and application of bifurcations in systems with impacts and chattering(Italy:Ph.D.thesis,University of Naples-FedericoⅡNaples) PACC:0547 Chattering bifurcations in a Duffing unilateral vibro-impact system* Feng Jin-Qian1)2)†Xu Wei1)Niu Yu-Jun1) 27 March 2009;revised manuscript 26 April 2009) A tail-mapping is introduced to deal with the tail impacts caused by the chattering,and based on which,an effective numerical method is suggested to simulate the chattering in the vibro-impact system.As an illustrative example,a Duffing unilateral vibro-impact system is investigated.The results show the evidence of complete and incomplete chattering.We also investigate two novel chattering bifurcations,including transitions from complete to incomplete chattering and incomplete chattering period to aperiodic motion. Duffing vibro-impact system,tail mapping,chattering bifurcation *国家自然科学基金(批准号:10872165)资助的课题. †E-mail:fengjinqian@mail.nwpu.edu.cn *Project supported by the National Natural Science Foundation of China(Grant No.10872165). †E-mail:fengjinqian@mail.nwpu.edu.cn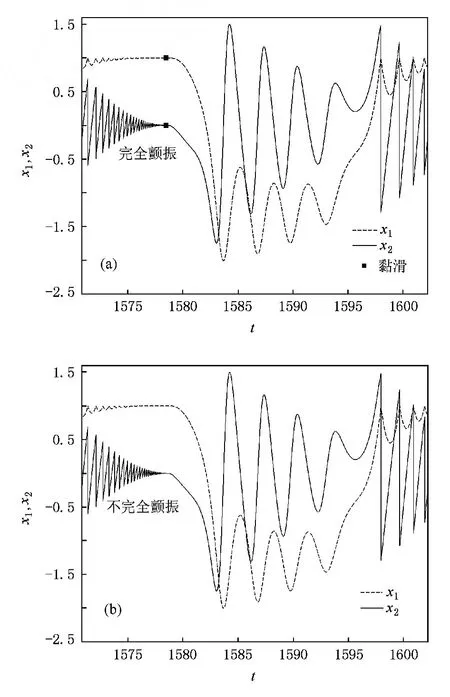

3.2.不完全颤振中擦边诱导的周期运动到拟周期运动的分岔


4.结论
1)(Department of Applied Mathematics,Northwestern Polytechnical University,Xi'an 710072,China)
2)(College of Science of Xi'an Polytechnic University,Xi'an710048,China)
